Двойной график

Красный график является двойственным графиком синего графика, и наоборот .

В математической дисциплине теории графов двойственный граф плоского графа G это граф, который имеет для каждой грани G. — вершину Двойственный граф имеет ребро для каждой пары граней в G , которые отделены друг от друга ребром, и замкнутую петлю , когда одна и та же грань появляется по обе стороны ребра. Таким образом, каждому ребру e графа G соответствует двойственное ребро, конечные точки которого являются двойственными вершинами, соответствующими граням по обе стороны от e . Определение двойственного зависит от выбора вложения графа G , поэтому это свойство плоских графов (графов, которые уже внедрены в плоскость), а не плоских графов (графов, которые могут быть встроены, но для которых вложение ограничено). пока не известно). Для плоских графов обычно может быть несколько двойственных графов, в зависимости от выбора планарного вложения графа.

формой двойственности Исторически первой признанной графов было объединение Платоновых тел в пары двойственных многогранников . Двойственность графа является топологическим обобщением геометрических понятий двойственных многогранников и двойственных мозаик и, в свою очередь, комбинаторно обобщается понятием двойственного матроида . Вариации двойственности планарных графов включают версию двойственности для ориентированных графов и двойственность для графов, встроенных в неплоские двумерные поверхности.

Эти понятия двойственных графов не следует путать с другим понятием - двойственным от ребра к вершине или линейным графом графа.

Термин «двойственный» что свойство быть двойственным графом является симметричным , а это означает, что если H является двойственным связному графу G , то G является двойственным графу H. используется потому , При обсуждении двойственного графа G сам граф G можно называть «первичным графом». Многие другие свойства и структуры графа могут быть переведены в другие естественные свойства и структуры двойственного графа. Например, циклы двойственны разрезам , остовные деревья двойственны дополнениям к остовным деревьям, а простые графы (без параллельных ребер или петель ) двойственны 3-реберно-связным графам .

Двойственность графов может помочь объяснить структуру лабиринтов и водосборных бассейнов . Двойные графы также применяются в компьютерном зрении , вычислительной геометрии , создании сеток и проектировании интегральных схем .

Примеры

Циклы и диполи

Дипольный график

цикла График

Уникальное планарное вложение графа цикла делит плоскость только на две области, внутреннюю и внешнюю, по теореме Жордана о кривой . Однако в n -цикле эти две области отделены друг от друга n различными ребрами. Следовательно, двойственный граф n -цикла представляет собой мультиграф с двумя вершинами (дуальными областям), соединенными друг с другом n дуальными ребрами. Такой граф называется кратным ребром, графом связи или иногда дипольным графом . И наоборот, двойственный дипольному графу с n -ребрами является n -циклом.

Двойные многогранники

Основная статья: Двойной многогранник

Куб и правильный октаэдр являются двойственными графами друг другу.

Согласно теореме Стейница , каждый многогранный граф (граф, образованный вершинами и ребрами трехмерного выпуклого многогранника ) должен быть плоским и 3-вершинно связным , а каждый 3-вершинно-связный плоский граф происходит из выпуклого многогранника в Сюда. Каждый трехмерный выпуклый многогранник имеет двойственный многогранник ; двойственный многогранник имеет вершину для каждой грани исходного многогранника, причем две двойственные вершины смежны всякий раз, когда соответствующие две грани имеют общее ребро. Если два многогранника двойственны, то и их графики двойственны. Например, Платоновы тела существуют в виде двойственных пар: октаэдр, двойственный кубу, додекаэдр, двойственный икосаэдру, и тетраэдр, двойственный самому себе. Двойственность многогранников также может быть расширена до двойственности многогранников более высоких размерностей . но это расширение геометрической двойственности не имеет четкой связи с теоретико-графовой двойственностью.

Самодуальные графы

Самодуальный граф.

Плоский граф называется самодвойственным, если он изоморфен своему двойственному графу. Колесообразные графы представляют собой бесконечное семейство самодвойственных графов, происходящих из самодвойственных многогранников ( пирамид ). Однако существуют также самодвойственные графы, которые не являются многогранниками, например показанный. Серватиус и Кристофер (1992) описывают две операции: слипание и взрыв, которые можно использовать для построения самодуального графа, содержащего заданный плоский граф; например, показанный самодвойственный граф может быть построен как сцепление тетраэдра с его двойственным.

следует Из формулы Эйлера , что каждый самодвойственный граф с n вершинами имеет ровно 2 n − 2 ребра. Каждый простой самодуальный планарный граф содержит не менее четырех вершин степени три, а каждое самодвойственное вложение имеет не менее четырех треугольных граней.

Характеристики

Многие естественные и важные концепции теории графов соответствуют другим столь же естественным, но отличным концепциям двойственного графа. Поскольку двойственный связному плоскому графу изоморфен простому графу, каждая из этих пар является двунаправленной: если понятие X в плоском графе соответствует понятию Y в двойственном графе, то понятие Y в плоском графе соответствует понятию X в двойственном графе.

Простые графы против мультиграфов

Двойственный графу не обязательно должен быть простым: он может иметь петли (ребро с обеими конечными точками в одной и той же вершине) или несколько ребер, соединяющих одни и те же две вершины, как уже было очевидно на примере дипольных мультиграфов, двойственных к циклические графики. В качестве частного случая двойственности сокращенного цикла, обсуждаемой ниже,мосты находятся во планарного графа G взаимно однозначном соответствии с петлями двойственного графа. По той же причине пара параллельных ребер в двойственном мультиграфе (то есть цикле длины 2) соответствует 2-реберному разрезу в простом графе (паре ребер, удаление которых разъединяет граф). Следовательно, планарный граф является простым тогда и только тогда, когда его двойственный граф не имеет 1- или 2-реберных разрезов; то есть, если он 3-реберно-связен . Простые плоские графы, двойники которых просты, являются в точности простыми планарными графами с 3-реберной связностью. Этот класс графов включает, но не совпадает с классом простых плоских графов с 3 вершинами связности . Например, рисунок, показывающий самодвойственный граф, является 3-реберно-связным (и, следовательно, его двойственный граф прост), но не 3-вершинно-связен.

Уникальность

Два красных графа двойственны синему, но не изоморфны .

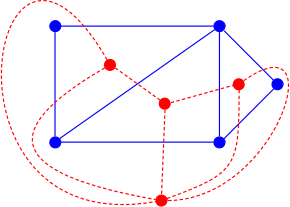
Поскольку двойственный граф зависит от конкретного вложения, двойственный граф планарному графу не уникален в том смысле, что один и тот же планарный граф может иметь неизоморфные двойственные графы. На рисунке синие графы изоморфны, а их двойственные красные графы — нет. Верхний красный двойственный граф имеет вершину степени 6 (соответствует внешней грани синего графа), тогда как в нижнем красном графе все степени меньше 6.

Хасслер-Уитни показал, что если граф 3-связен, то вложение и, следовательно, двойственный граф уникальны. По теореме Стейница эти графы являются в точности графами многогранников , графами выпуклых многогранников. Планарный граф является 3-вершинно связным тогда и только тогда, когда его двойственный граф 3-вершинно связен. В более общем смысле, планарный граф имеет уникальное вложение и, следовательно, уникальный двойственный граф тогда и только тогда, когда он является подразделением планарного графа, связанного с 3 вершинами (графа, образованного из планарного графа, связанного с 3 вершинами путем замены некоторые его ребра по путям). Для некоторых плоских графов, которые не являются 3-связными, таких как полный двудольный граф K _2,4 , вложение не уникально, но все вложения изоморфны. Соответственно, когда это происходит, все двойственные графы изоморфны.

Поскольку разные вложения могут привести к разным двойственным графам, проверка того, является ли один граф двойственным другому (без знания их вложений), является нетривиальной алгоритмической проблемой. Для двусвязных графов ее можно решить за полиномиальное время, используя SPQR-деревья графов для построения канонической формы наличия отношения эквивалентности общего взаимного двойственного отношения. Например, два красных графика на иллюстрации эквивалентны согласно этому соотношению. Однако для плоских графов, которые не являются двусвязными, это отношение не является отношением эквивалентности, и проблема проверки взаимной двойственности является NP-полной .

Разрезы и циклы

Набор разрезов в произвольном связном графе — это подмножество ребер, определенное путем разделения вершин на два подмножества путем включения ребра в подмножество, когда оно имеет по одной конечной точке на каждой стороне разделения. Удаление ребер разреза обязательно разбивает граф как минимум на две компоненты связности. Минимальный набор разрезов (также называемый связью) — это набор разрезов, обладающий тем свойством, что каждое правильное подмножество набора разрезов само по себе не является разрезом. Минимальный разрез связного графа обязательно разделяет его граф ровно на два компонента и состоит из набора ребер, имеющих по одной конечной точке в каждом компоненте. Простой цикл — это связный подграф , в котором каждая вершина цикла инцидентна ровно двум ребрам цикла.

В связном плоском графе G каждый простой цикл G соответствует минимальному разрезу в двойственном графе G , и наоборот. Это можно рассматривать как форму теоремы о жордановой кривой : каждый простой цикл разделяет грани G на грани внутри цикла и грани вне цикла, а двойственные ребра цикла являются в точности гранями, двойственными ребрам цикла. края, переходящие изнутри наружу. Обхват его любого плоского графа (размер его наименьшего цикла) равен связности ребер двойственного графа (размеру его наименьшего сечения).

Эта двойственность распространяется от отдельных разрезов и циклов до векторных пространств, определенных на их основе. Пространство циклов графа определяется как семейство всех подграфов, имеющих четную степень в каждой вершине; его можно рассматривать как векторное пространство над двухэлементным конечным полем , где симметричная разность двух наборов ребер действует как операция сложения векторов в векторном пространстве. Аналогично, пространство разреза графа определяется как семейство всех наборов разрезов с добавлением векторов, определяемым таким же образом. Тогда пространство циклов любого плоского графа и пространство сечения двойственного ему графа изоморфны как векторные пространства. Таким образом, ранг планарного графа ( размерность его разреза) равен круговому числу его двойственного графа (размерность его пространства циклов) и наоборот. Базис циклов графа — это набор простых циклов, образующих базис пространства циклов (каждый подграф четной степени может быть образован ровно одним способом как симметричная разность некоторых из этих циклов). Для плоских графов, взвешенных по ребрам (с достаточно общими весами, чтобы никакие два цикла не имели одинаковый вес), базис цикла графа с минимальным весом двойственен дереву Гомори – Ху двойственного графа, набору вложенных разрезов, которые вместе включают в себя минимальный разрез, разделяющий каждую пару вершин графа. Каждый цикл в базисе цикла минимального веса имеет набор ребер, двойственных ребрам одного из разрезов дерева Гомори–Ху. Когда веса циклов могут быть связаны, базис цикла с минимальным весом может не быть уникальным, но в этом случае все равно верно, что дерево Гомори – Ху двойственного графа соответствует одной из баз циклов с минимальным весом графа.

В ориентированных плоских графах простые направленные циклы двойственны направленным разрезам (разбиению вершин на два подмножества так, что все ребра идут в одном направлении, от одного подмножества к другому). Сильно ориентированные планарные графы (графы, основной неориентированный граф которых связен и в которых каждое ребро принадлежит циклу) двойственны ориентированным ациклическим графам , в которых ни одно ребро не принадлежит циклу. Другими словами, сильные ориентации связного планарного графа (назначения направлений ребрам графа, которые приводят к сильно связному графу ) двойственны ациклическим ориентациям (назначения направлений, которые создают ориентированный ациклический граф ). Точно так же дисоединения (наборы ребер, включающие ребра из каждого направленного разреза) двойственны наборам дуг обратной связи (наборам ребер, включающим ребра из каждого цикла).

Связывающиеся деревья

Простой лабиринт, в котором стены лабиринта и свободное пространство между стенами образуют два пересекающихся дерева.

Остовное дерево можно определить как набор ребер, который вместе со всеми вершинами графа образует связный ациклический подграф. Но в силу двойственности разрезного цикла, если множество S ребер в плоском графе G ациклично (не имеет циклов), то множество ребер, двойственных к S, не имеет разрезов, из чего следует, что дополнительное множество двойственных ребер (двойственные ребра, не входящие в S ) образуют связный подграф. Симметрично, если S связен, то ребра, двойственные дополнению к S, образуют ациклический подграф. Следовательно, когда S обладает обоими свойствами – связностью и ацикличностью – то же самое верно и для дополнительного множества в двойственном графе. То есть каждое остовное дерево G дополняет остовное дерево двойственного графа, и наоборот. Таким образом, ребра любого плоского графа и его двойственного графа могут быть вместе разделены (несколько различных способов) на два остовных дерева, одно в простом и одно в двойственном графе, которые вместе распространяются на все вершины и грани графа, но никогда пересекать друг друга. В частности, минимальное остовное дерево дополняет G максимальное остовное дерево двойственного графа. Однако это не работает для деревьев кратчайших путей , даже приблизительно: существуют плоские графы такие, что для каждой пары остовного дерева в графе и дополнительного остовного дерева в двойственном графе по крайней мере одно из двух деревьев имеет расстояния которые значительно длиннее расстояний на его графике.

Пример такого типа разложения на взаимосвязанные деревья можно увидеть в некоторых простых типах лабиринтов с единственным входом и отсутствием разъединенных компонентов его стен. В этом случае и стены лабиринта, и пространство между стенами принимают форму математического дерева. Если свободное пространство лабиринта разделено на простые ячейки (например, квадраты сетки), то эту систему ячеек можно рассматривать как вложение плоского графа, в котором древовидная структура стен образует остовное дерево граф и древовидная структура свободного пространства образуют остовное дерево двойственного графа. Подобные пары переплетающихся деревьев также можно увидеть в древовидном узоре ручьев и рек в водосборном бассейне , а также в двойном древовидном узоре хребтов, разделяющих ручьи.

Это разбиение ребер и их двойников на два дерева приводит к простому доказательству формулы Эйлера V − E + F = 2 для плоских графов с V вершинами, E ребрами и F гранями. Любое остовное дерево и дополняющее его двойственное остовное дерево делят ребра на два подмножества из V - 1 и F - 1 ребер соответственно, а сложение размеров двух подмножеств дает уравнение

Е = ( V - 1) + ( F - 1)

которую можно переставить, чтобы сформировать формулу Эйлера. По мнению Дункана Соммервилля , это доказательство формулы Эйлера основано на » КГК фон Штаудта «Геометрии дер Лаге (Нюрнберг, 1847).

В неплоских поверхностных вложениях множество двойственных ребер, дополнительных к остовному дереву, не является двойственным остовным деревом. Вместо этого этот набор ребер представляет собой объединение двойственного остовного дерева с небольшим набором дополнительных ребер, количество которых определяется родом поверхности, на которую вложен граф. Дополнительные ребра в сочетании с путями в остовных деревьях можно использовать для создания фундаментальной группы поверхности.

Дополнительные свойства

Любая формула подсчета, включающая вершины и грани, верная для всех планарных графов, может быть преобразована с помощью планарной двойственности в эквивалентную формулу, в которой роли вершин и граней поменялись местами. Одним из примеров является формула Эйлера, которая является самодвойственной. Другая, предложенная Харари, включает в себя лемму о рукопожатии , согласно которой сумма степеней вершин любого графа равна удвоенному количеству ребер. В своей двойственной форме эта лемма утверждает, что в плоском графе сумма чисел сторон граней графа равна удвоенному числу ребер.

Медиальный граф плоского графа изоморфен медиальному графу его двойственного графа. Два плоских графа могут иметь изоморфные медиальные графы, только если они двойственны друг другу.

Планарный граф с четырьмя или более вершинами является максимальным (нельзя добавлять больше ребер при сохранении планарности) тогда и только тогда, когда его двойственный граф одновременно 3-связен и 3-регулярен .

Связный планарный граф является эйлеровым (имеет четную степень в каждой вершине) тогда и только тогда, когда его двойственный граф двудольный . Гамильтонов цикл в плоском графе G соответствует разбиению вершин двойственного графа на два подмножества (внутреннее и внешнее цикла), оба индуцированных подграфа которых являются деревьями. В частности, гипотеза Барнетта о гамильтоновости кубических двудольных многогранных графов эквивалентна гипотезе о том, что каждый эйлеров максимальный планарный граф можно разбить на два индуцированных дерева.

Если планарный граф G имеет Татта TG _{полином} ( x , y ) , то полином Тутте его двойственного графа получается путем замены x и y . По этой причине, если какое-то конкретное значение полинома Тутте предоставляет информацию об определенных типах структур в G , то замена аргументов полинома Тутте даст соответствующую информацию для двойственных структур. Например, количество сильных ориентаций равно TG _{, а} (0,2) количество ациклических ориентаций — ( _TG 2,0) . Для без мостов плоских графов раскраска графа в k цветов соответствует потокам, не имеющим нигде нуля по модулю k, на двойственном графе. Например, теорема о четырех цветах (существование 4-раскраски для каждого планарного графа) может быть эквивалентно выражена как утверждение, что двойственный элемент каждого планарного графа без мостов имеет нигде ненулевой 4-поток. Количество k -раскрасок подсчитывается (с точностью до легко вычислимого коэффициента) по значению полинома Татта TG _k (1 − k ,0) , а количество нигде ненулевых -потоков подсчитывается по значению ( _TG 0,1 - к ) .

St - планарный граф — это связный планарный граф вместе с биполярной ориентацией этого графа, ориентацией, которая делает его ациклическим с одним источником и одним приемником, оба из которых должны находиться на одной грани друг с другом. Такой граф можно превратить в сильно связный граф, добавив еще одно ребро от стока обратно к истоку через внешнюю грань. Двойник этого расширенного планарного графа сам по себе является дополнением другого st -планарного графа.

Вариации

Ориентированные графы

В ориентированном плоском графе двойственный граф также можно сделать ориентированным, ориентируя каждое двойственное ребро на 90° по часовой стрелке от соответствующего основного ребра. Строго говоря, эта конструкция не является двойственностью ориентированных плоских графов, поскольку, начиная с графа G мы не возвращаемся к самому G , а вместо этого конструируем граф, изоморфный транспонированному графу G и дважды беря двойственный граф , , граф, образованный из G перевернув все его края. Четырехкратное взятие двойного числа возвращает исходный график.

Слабый двойной

Слабый двойственный плоскому графу — это подграф двойственного графа, вершины которого соответствуют ограниченным граням простого графа. Плоский граф является внешнепланарным тогда и только тогда, когда его слабый двойник является лесом . Для любого плоского графа G пусть G ⁺ быть плоским мультиграфом, образованным путем добавления одной новой вершины v в неограниченную грань G и соединения v с каждой вершиной внешней грани (несколько раз, если вершина появляется несколько раз на границе внешней грани); тогда G является слабым двойственным к (плоскому) двойственному к G ⁺ .

Бесконечные графы и тесселяции

Концепция двойственности применима как к бесконечным графам, вложенным в плоскость, так и к конечным графам. Однако необходимо проявлять осторожность, чтобы избежать топологических осложнений, таких как точки плоскости, которые не являются ни частью открытой области, не пересекающейся с графом, ни частью ребра или вершины графа. Когда все грани представляют собой ограниченные области, окруженные циклом графа, вложение бесконечного плоского графа также можно рассматривать как мозаику плоскости, покрытие плоскости замкнутыми дисками (плитки мозаики), внутренние части которых (грани вложения) представляют собой непересекающиеся открытые диски. Плоская двойственность порождает понятие двойной мозаики — мозаики, образованной путем размещения вершины в центре каждой плитки и соединения центров соседних плиток.

Диаграмма Вороного (красный) и триангуляция Делоне (черный) конечного множества точек (черные точки)

Концепция двойной мозаики также может быть применена к разбиению плоскости на конечное число областей. В данном случае это тесно связано с двойственностью планарного графа, но не совсем то же самое. Например, диаграмма Вороного конечного набора точечных узлов представляет собой разбиение плоскости на многоугольники , внутри которых один узел находится ближе, чем любой другой. Точки на выпуклой оболочке входных данных образуют неограниченные многоугольники Вороного, две стороны которых представляют собой бесконечные лучи, а не конечные отрезки прямых. Двойником этой диаграммы является входная триангуляция Делоне , плоский граф, соединяющий два узла ребром всякий раз, когда существует круг, содержащий эти два узла и не содержащий других узлов. Края выпуклой оболочки входа также являются краями триангуляции Делоне, но они соответствуют лучам, а не отрезкам прямой диаграммы Вороного. Эту двойственность между диаграммами Вороного и триангуляциями Делоне можно превратить в двойственность между конечными графами одним из двух способов: добавив искусственную вершину на бесконечности к диаграмме Вороного, чтобы служить другой конечной точкой для всех ее лучей, или рассматривая ограниченную часть диаграммы Вороного как слабую двойственную триангуляцию Делоне. Хотя диаграмма Вороного и триангуляция Делоне двойственны, их вложение в плоскость может иметь дополнительные пересечения помимо пересечений двойственных пар ребер. Каждая вершина треугольника Делоне расположена внутри соответствующей грани диаграммы Вороного. Каждая вершина диаграммы Вороного расположена в центре описанной окружности соответствующего треугольника триангуляции Делоне, но эта точка может лежать вне ее треугольника.

Неплоские вложения

K ₇ двойственен графу Хивуда в торе

K6 _на двойственен графу Петерсена проективной плоскости

Понятие двойственности можно распространить на вложения графов на двумерных многообразиях, отличных от плоскости. Определение то же самое: существует двойственная вершина для каждой связной компоненты дополнения графа в многообразии и двойственное ребро для каждого ребра графа, соединяющее две двойственные вершины по обе стороны от ребра. В большинстве приложений этой концепции она ограничивается вложениями, каждая грань которых является топологическим диском; это ограничение обобщает требование связности графа для плоских графов. С этим ограничением двойственный граф любого вложенного в поверхность графа имеет естественное вложение на ту же поверхность, так что двойственный граф изоморфен исходному графу и изоморфно вложен в него. Например, полный граф K ₇ является тороидальным : он не плоский, но может быть вложен в тор, причем каждая грань вложения представляет собой треугольник. этого вложения является граф Хивуда . Двойственным графом

Та же концепция одинаково хорошо работает и для неориентируемых поверхностей . Например, K ₆ может быть вложен в проективную плоскость с десятью треугольными гранями в виде полуикосаэдра , двойственным которому является граф Петерсена, вложенный в виде полудодекаэдра .

Даже плоские графы могут иметь неплоские вложения с двойственными графами, производными от тех вложений, которые отличаются от их плоских двойственных графов. Например, четыре многоугольника Петри куба (шестиугольники, образованные удалением двух противоположных вершин куба) образуют шестиугольные грани вложения куба в тор . Двойственный граф этого вложения имеет четыре вершины, образующие полный граф K ₄ с удвоенными ребрами. При вложении тора этого двойственного графа шесть ребер, инцидентных каждой вершине, в циклическом порядке вокруг этой вершины дважды циклически проходят через три другие вершины. В отличие от ситуации на плоскости, это вложение куба и его двойника не уникально; граф куба имеет несколько других вложений тора с разными двойниками.

Многие из эквивалентностей между свойствами простых и двойственных графов планарных графов не могут быть обобщены на непланарные двойственные графы или требуют дополнительной осторожности при их обобщении.

Другая операция над графами, внедренными на поверхность, — это двойственная операция Петри , которая использует многоугольники Петри вложения в качестве граней нового вложения. В отличие от обычного двойственного графа, он имеет те же вершины, что и исходный граф, но лежит, как правило, на другой поверхности. Поверхностная двойственность и двойственность Петри — две из шести операций Вильсона , которые вместе образуют группу этих операций.

Матроиды и алгебраические двойственные числа

Алгебраическим двойственным связному графу G называется граф G ^* такие, что G и G ^* имеют одинаковый набор ребер цикл G G является разрезом , любой ^* , и любой разрез G является циклом G ^* . Каждый планарный граф имеет двойственный алгебраический граф, который, вообще говоря, не уникален (подойдет любой двойственный граф, определенный вложением плоскости). На самом деле верно обратное, как установил Хасслер Уитни в критерии планарности Уитни :

Связный граф G является плоским тогда и только тогда, когда он имеет двойственный алгебраический граф.

Тот же факт можно выразить в теории матроидов . Если M — графический матроид графа G , то граф G ^* является алгебраически двойственным к G тогда и только тогда, когда графический матроид G ^* является матроидом M . двойственным Тогда критерий планарности Уитни можно перефразировать следующим образом: двойственный матроид графического матроида M сам по себе является графическим матроидом тогда и только тогда, когда лежащий в основе граф G графа M планарен. Если G планарен, двойственный матроид является графическим матроидом двойственного графа G . В частности, все двойственные графы для всех различных плоских вложений G имеют изоморфные графические матроиды.

Для неплоских поверхностных вложений, в отличие от плоских двойственных графов, двойственный граф обычно не является алгебраически двойственным к простому графу. А для непланарного графа G двойственный матроид графического матроида G сам по себе не является графическим матроидом. прежнему матроид, схемы которого соответствуют разрезам в G , и в этом смысле его можно рассматривать как комбинаторно обобщенный алгебраический двойственный элемент к G. Однако это по -

Двойственность между эйлеровыми и двудольными плоскими графами может быть распространена на бинарные матроиды (которые включают графические матроиды, полученные из плоских графов): бинарный матроид является эйлеровым тогда и только тогда, когда его двойственный матроид является двудольным .

Две двойственные концепции обхвата и связности ребер объединены в теории матроида обхватом матроида : обхват графического матроида плоского графа такой же, как обхват графа, а обхват двойственного матроида (графический матроид двойственного графа) граф) — это связность ребер графа.

Приложения

Помимо использования в теории графов, двойственность плоских графов находит применение в ряде других областей математических и вычислительных исследований.

В географических информационных системах сети потоков (например, сети, показывающие, как вода течет в системе ручьев и рек) двойственны сотовым сетям, описывающим водоразделы . Эту двойственность можно объяснить, моделируя сеть потоков в виде остовного дерева на сеточном графе соответствующего масштаба и моделируя водораздел в виде дополнительного остовного дерева хребтовых линий на сеточном графе с двойной сеткой.

В компьютерном зрении цифровые изображения разбиваются на небольшие квадратные пиксели , каждый из которых имеет свой цвет. Двойной граф этого подразделения на квадраты имеет вершину на пиксель и ребро между парами пикселей, которые имеют общее ребро; это полезно для приложений, включающих кластеризацию пикселей в связанные области схожих цветов.

В вычислительной геометрии двойственность между диаграммами Вороного и триангуляциями Делоне подразумевает, что любой алгоритм построения диаграммы Вороного можно сразу преобразовать в алгоритм триангуляции Делоне, и наоборот. Та же двойственность может быть использована и при конечных элементов создании сетки . Алгоритм Ллойда , метод, основанный на диаграммах Вороного для перемещения набора точек на поверхности в более равномерно расположенные положения, обычно используется как способ сглаживания сетки конечных элементов, описываемой двойной триангуляцией Делоне. Этот метод улучшает сетку, делая ее треугольники более однородными по размеру и форме.

При синтезе КМОП - схем синтезируемая функция представляется в виде формулы булевой алгебры . Затем эта формула переводится в два последовательно-параллельных мультиграфа . Эти графики можно интерпретировать как принципиальные схемы , в которых края графиков представляют собой транзисторы , управляемые входами функции. Одна схема вычисляет саму функцию, а другая — ее дополнение. Одна из двух схем получается путем преобразования конъюнкций и дизъюнкций формулы в последовательные и параллельные композиции графов соответственно. Другая схема меняет эту конструкцию, преобразуя конъюнкции и дизъюнкции формулы в параллельные и последовательные композиции графов. Эти две схемы, дополненные дополнительным ребром, соединяющим вход каждой схемы с ее выходом, представляют собой планарные двойственные графы.

История

Двойственность выпуклых многогранников была признана Иоганном Кеплером в его книге «Harmonices Mundi» 1619 года . Узнаваемые плоские двойственные графы, вне контекста многогранников, появились еще в 1725 году в Пьера Вариньона « посмертно опубликованной работе Новая механика или статика» . Это было еще до выхода в Леонарда Эйлера 1736 году работы о семи мостах Кенигсберга , которую часто считают первой работой по теории графов . Вариньон проанализировал силы, действующие на статические системы стоек, нарисовав график, двойственный стойкам, с длинами ребер, пропорциональными силам на стойках; этот двойственный граф является разновидностью диаграммы Кремоны . В связи с теоремой о четырех цветах двойственные графики карт (подразделения плоскости на области) были упомянуты Альфредом Кемпе в 1879 году и распространены на карты на неплоских поверхностях Лотаром Хеффтером в 1891 году. Двойственность как операция над абстрактными плоскими графами была введена Хасслером Уитни в 1931 году.

Внешние ссылки

• Вайсштейн, Эрик В. , «Двойной граф» , MathWorld