✖
~~~~~~~~~~~~~~~~~~~~ Arc.Ask3.Ru ~~~~~~~~~~~~~~~~~~~~~ 
Номер скриншота №:
✰ BDC1043974C524C7B62DF1413EFD5812__1717763820 ✰
Заголовок документа оригинал.:
✰ List of Mersenne primes and perfect numbers - Wikipedia ✰
Заголовок документа перевод.:
✰ Список простых и совершенных чисел Мерсенна — Википедия ✰
Снимок документа находящегося по адресу (URL):
✰ https://en.wikipedia.org/wiki/List_of_Mersenne_primes_and_perfect_numbers ✰
Адрес хранения снимка оригинал (URL):
✰ https://arc.ask3.ru/arc/aa/bd/12/bdc1043974c524c7b62df1413efd5812.html ✰
Адрес хранения снимка перевод (URL):
✰ https://arc.ask3.ru/arc/aa/bd/12/bdc1043974c524c7b62df1413efd5812__translat.html ✰
Дата и время сохранения документа:
✰ 09.06.2024 04:57:45 (GMT+3, MSK) ✰
Дата и время изменения документа (по данным источника):
✰ 7 June 2024, at 15:37 (UTC). ✰ 

~~~~~~~~~~~~~~~~~~~~~~ Ask3.Ru ~~~~~~~~~~~~~~~~~~~~~~ 
Сервисы Ask3.ru: 
 Архив документов (Снимки документов, в формате HTML, PDF, PNG - подписанные ЭЦП, доказывающие существование документа в момент подписи. Перевод сохраненных документов на русский язык.) 
✰ https://arc.ask3.ru ✰
 Ответы на вопросы (Сервис ответов на вопросы, в основном, научной направленности) 
✰ https://ask3.ru/answer2question ✰
 Товарный сопоставитель (Сервис сравнения и выбора товаров) ✰✰
✰ https://ask3.ru/product2collation ✰
 Партнеры 
✰ https://comrades.ask3.ru ✰


Совет. Чтобы искать на странице, нажмите Ctrl+F или ⌘-F (для MacOS) и введите запрос в поле поиска.
Список простых и совершенных чисел Мерсенна — Jump to content

Список простых чисел Мерсенна и совершенных чисел

Из Википедии, бесплатной энциклопедии

Палочки Кюизенера, показывающие правильные делители 6 (1, 2 и 3), в сумме дающие 6.
Визуализация числа 6 как идеального числа
График, на котором годы отложены по оси X, а количество цифр наибольшего известного простого числа логарифмировано по оси Y, с двумя линиями тренда.
Логарифмический график количества цифр наибольшего известного простого числа по годам, почти все из которых были простыми числами Мерсенна.

Простые числа Мерсенна и совершенные числа — это два глубоко взаимосвязанных типа натуральных чисел в теории чисел . Простые числа Мерсенна, названные в честь монаха Марина Мерсенна , представляют собой простые числа , которые можно выразить как 2. п − 1 для некоторого положительного целого числа p . Например, 3 — простое число Мерсенна, поскольку это простое число и выражается как 2. 2 − 1 . [1] [2] Числа p , соответствующие простым числам Мерсенна, сами должны быть простыми, хотя не все простые числа p приводят к простым числам Мерсенна, например, 2 11 − 1 = 2047 = 23 × 89 . [3] Между тем, совершенные числа — это натуральные числа , которые равны сумме своих положительных собственных делителей , которые являются делителями, исключая само число. Итак, 6 — совершенное число, потому что собственные делители 6 — 1, 2 и 3 , а также 1 + 2 + 3 = 6 . [2] [4]

существует взаимно однозначное соответствие Между простыми числами Мерсенна и четными совершенными числами . Это связано с теоремой Евклида-Эйлера , частично доказанной Евклидом и дополненной Леонардом Эйлером : четные числа совершенны тогда и только тогда, когда их можно выразить в форме 2 п - 1 × (2 п − 1) , где 2 п − 1 — простое число Мерсенна. Другими словами, все числа, соответствующие этому выражению, являются совершенными, а все даже совершенные числа соответствуют этой форме. Например, в случае p = 2 , 2 2 − 1 = 3 — простое число, а 2 2 − 1 × (2 2 − 1) = 2 × 3 = 6 является совершенным. [1] [5] [6]

В настоящее время остается открытой проблема , существует ли бесконечное число простых чисел Мерсенна и даже совершенных чисел. [2] [6] Частота простых чисел Мерсенна является предметом гипотезы Ленстры-Померанса-Вагстаффа , которая утверждает, что ожидаемое количество простых чисел Мерсенна меньше некоторого заданного x равно ( e с / log 2) × log log x , где e — число Эйлера , γ — константа Эйлера , а log — натуральный логарифм . [7] [8] [9] Также неизвестно, существуют ли какие-либо нечетные совершенные числа; были доказаны различные условия возможных нечетных совершенных чисел, включая нижнюю границу 10 . 1500 . [10]

Ниже приводится список всех известных в настоящее время простых и совершенных чисел Мерсенна, а также их соответствующие показатели степени p . По состоянию на 2023 год Известно 51 простое число Мерсенна (и, следовательно, совершенные числа), 17 крупнейших из которых были обнаружены в рамках распределенных вычислений проекта Great Internet Mersenne Prime Search или GIMPS. [2] Новые простые числа Мерсенна находятся с помощью теста Лукаса-Лемера (LLT), теста на простоту простых чисел Мерсенна, который эффективен для двоичных компьютеров. [2]

Отображаемые ранги относятся к числу индексов, известных на данный момент по состоянию на 2022 год. ; while unlikely, ranks may change if smaller ones are discovered. According to GIMPS, all possibilities less than the 48th working exponent p = 57,885,161 have been checked and verified as of January 2024. [11] Год открытия и первооткрыватель относятся к простому числу Мерсенна, поскольку совершенное число сразу следует из теоремы Евклида-Эйлера. Первооткрыватели, обозначенные как «GIMPS / имя », относятся к открытиям GIMPS с использованием оборудования, используемого этим человеком. Более поздние записи очень длинные, поэтому отображаются только первые и последние шесть цифр каждого номера.

Таблица всех 51 известного на данный момент простого числа Мерсенна и соответствующих им совершенных чисел
Классифицировать п Мерсенн премьер Простые цифры Мерсенна Идеальное число Совершенные цифры числа Открытие Исследователь Метод Ссылка. [12]
1 2 3 1 6 1 Древние времена [а] Известен древнегреческим математикам. Незаписанный [13] [14] [15]
2 3 7 1 28 2 [13] [14] [15]
3 5 31 2 496 3 [13] [14] [15]
4 7 127 3 8128 4 [13] [14] [15]
5 13 8191 4 33550336 8 1200 с/c. 1456 [б] Несколько [с] Пробное подразделение [14] [15]
6 17 131071 6 8589869056 10 1588 [б] Пьетро Катальди [2] [18]
7 19 524287 6 137438691328 12 [2] [18]
8 31 2147483647 10 230584...952128 19 1772 Леонард Эйлер Пробное разделение с модульными ограничениями [19] [20]
9 61 230584...693951 19 265845...842176 37 Ноябрь 1883 г. Иван Первушин Последовательности Лукаса [21]
10 89 618970...562111 27 191561...169216 54 июнь 1911 г. Ральф Эрнест Пауэрс [22]
11 107 162259...288127 33 131640...728128 65 1 июня 1914 г. [23]
12 127 170141...105727 39 144740...152128 77 10 января 1876 г. Эдвард Лукас [24]
13 521 686479...057151 157 235627...646976 314 30 января 1952 г. Рафаэль М. Робинсон ООО « СВАК » [25]
14 607 531137...728127 183 141053...328128 366 [25]
15 1,279 104079...729087 386 541625...291328 770 25 июня 1952 г. [26]
16 2,203 147597...771007 664 108925...782528 1,327 7 октября 1952 г. [27]
17 2,281 446087...836351 687 994970...915776 1,373 9 октября 1952 г. [27]
18 3,217 259117...315071 969 335708...525056 1,937 8 сентября 1957 г. Ганс Ризель ООО «БЭСК» [28]
19 4,253 190797...484991 1,281 182017...377536 2,561 3 ноября 1961 г. Александр Гурвиц ЛЛТ на IBM 7090 [29]
20 4,423 285542...580607 1,332 407672...534528 2,663 [29]
21 9,689 478220...754111 2,917 114347...577216 5,834 11 мая 1963 г. Дональд Б. Гиллис ООО по ILLIAC II [30]
22 9,941 346088...463551 2,993 598885...496576 5,985 16 мая 1963 г. [30]
23 11,213 281411...392191 3,376 395961...086336 6,751 2 июня 1963 г. [30]
24 19,937 431542...041471 6,002 931144...942656 12,003 4 марта 1971 г. Брайант Такерман ЛЛТ на IBM 360/91 [31]
25 21,701 448679...882751 6,533 100656...605376 13,066 30 октября 1978 г. Лэндон Курт Нолл и Лаура Никель LLT на CDC Cyber ​​174 [32]
26 23,209 402874...264511 6,987 811537...666816 13,973 9 февраля 1979 г. Лэндон Курт Нолл [32]
27 44,497 854509...228671 13,395 365093...827456 26,790 8 апреля 1979 г. Гарри Л. Нельсон и Дэвид Словински ООО на Крей-1 [33] [34]
28 86,243 536927...438207 25,962 144145...406528 51,924 25 сентября 1982 г. Дэвид Словински [35]
29 110,503 521928...515007 33,265 136204...862528 66,530 29 января 1988 г. Уолтер Колкуитт и Люк Уэлш ООО на NEC SX -2 [36] [37]
30 132,049 512740...061311 39,751 131451...550016 79,502 19 сентября 1983 г. Дэвид Словински и др. ( Крэй ) LLT по Cray X-MP [38]
31 216,091 746093...528447 65,050 278327...880128 130,100 1 сентября 1985 г. LLT на Cray X-MP/24 [39] [40]
32 756,839 174135...677887 227,832 151616...731328 455,663 17 февраля 1992 г. LLT по Harwell Lab лаборатории Cray-2 [41]
33 859,433 129498...142591 258,716 838488...167936 517,430 4 января 1994 г. ООО на Cray C90 [42]
34 1,257,787 412245...366527 378,632 849732...704128 757,263 3 сентября 1996 г. ООО на Cray T94 [43] [44]
35 1,398,269 814717...315711 420,921 331882...375616 841,842 13 ноября 1996 г. GIMPS / Джоэл Арменго LLT / Prime95 90 МГц с процессором Pentium на ПК [45]
36 2,976,221 623340...201151 895,932 194276...462976 1,791,864 24 августа 1997 г. GIMPS / Гордон Спенс LLT / Prime95 на ПК с процессором Pentium 100 МГц [46]
37 3,021,377 127411...694271 909,526 811686...457856 1,819,050 27 января 1998 г. GIMPS / Роланд Кларксон LLT/Prime95 на ПК с процессором Pentium 200 МГц [47]
38 6,972,593 437075...193791 2,098,960 955176...572736 4,197,919 1 июня 1999 г. GIMPS / Наян Хаджратвала LLT/Prime95 на IBM Aptiva 350 МГц Pentium II с процессором [48]
39 13,466,917 924947...259071 4,053,946 427764...021056 8,107,892 14 ноября 2001 г. GIMPS / Майкл Кэмерон LLT/Prime95 на ПК с Athlon T-Bird процессором 800 МГц [49]
40 20,996,011 125976...682047 6,320,430 793508...896128 12,640,858 17 ноября 2003 г. GIMPS / Майкл Шафер LLT/Prime95 на ПК Dell Dimension 2 ГГц Pentium 4 с процессором [50]
41 24,036,583 299410...969407 7,235,733 448233...950528 14,471,465 15 мая 2004 г. GIMPS / Джош Финдли LLT/Prime95 на ПК с процессором Pentium 4 2,4 ГГц [51]
42 25,964,951 122164...077247 7,816,230 746209...088128 15,632,458 18 февраля 2005 г. GIMPS / Мартин Новак [52]
43 30,402,457 315416...943871 9,152,052 497437...704256 18,304,103 15 декабря 2005 г. GIMPS / Кертис Купер и Стивен Бун LLT / Prime95 на ПК в Университете Центрального Миссури [53]
44 32,582,657 124575...967871 9,808,358 775946...120256 19,616,714 4 сентября 2006 г. [54]
45 37,156,667 202254...220927 11,185,272 204534...480128 22,370,543 6 сентября 2008 г. GIMPS / Ханс-Михаэль Эльвених ООО / Prime95 на ПК [55]
46 42,643,801 169873...314751 12,837,064 144285...253376 25,674,127 4 июня 2009 г. [д] GIMPS / Одд Магнар Стриндмо LLT/Prime95 на ПК с Intel Core 2 процессором 3 ГГц [56]
47 43,112,609 316470...152511 12,978,189 500767...378816 25,956,377 23 августа 2008 г. GIMPS / Эдсон Смит LLT/Prime95 на ПК Dell OptiPlex с процессором Intel Core 2 Duo E6600 [55] [57] [58]
48 57,885,161 581887...285951 17,425,170 169296...130176 34,850,340 25 января 2013 г. GIMPS / Кертис Купер LLT / Prime95 на ПК в Университете Центрального Миссури [59] [60]
* 68,245,783 Самая низкая непроверенная веха [Это]
49 [ф] 74,207,281 300376...436351 22,338,618 451129...315776 44,677,235 7 января 2016 г. [г] GIMPS / Кертис Купер LLT/Prime95 на ПК с Intel Core процессором i7-4790 [61] [62]
50 [ф] 77,232,917 467333...179071 23,249,425 109200...301056 46,498,850 26 декабря 2017 г. GIMPS / Джонатан Пейс LLT/Prime95 на ПК с процессором Intel Core i5-6600 [63] [64]
51 [ф] 82,589,933 148894...902591 24,862,048 110847...207936 49,724,095 7 декабря 2018 г. GIMPS / Патрик Ларош LLT/Prime95 на ПК с процессором Intel Core i5-4590T [65] [66]
* 117,192,137 Самая низкая непроверенная веха [Это]

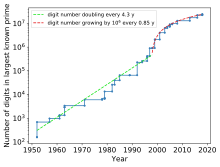
Исторически сложилось так, что самым большим известным простым числом часто было простое число Мерсенна.

Примечания [ править ]

  1. ↑ Первые четыре совершенных числа были задокументированы Никомахом около 100 г., и эта концепция была известна (вместе с соответствующими простыми числами Мерсенна) Евклиду во времена его «Начал» . Сведений об открытии нет.
  2. ^ Перейти обратно: а б Исламские математики , такие как Исмаил ибн Ибрагим ибн Фаллус (1194–1239), возможно, знали совершенные числа с пятого по седьмой до европейских рекордов. [16]
  3. ^ Найден в анонимной рукописи Clm 14908 , датированной 1456 и 1461 годами, а также в более ранней работе Ибн Фаллуса , которая не получила широкого распространения. [14] [17]
  4. ^ M 42,643,801 впервые было сообщено в GIMPS 12 апреля 2009 г., но не было замечено человеком до 4 июня 2009 г. из-за ошибки сервера.
  5. ^ Перейти обратно: а б По состоянию на 1 июня 2024 г. [11]
  6. ^ Перейти обратно: а б с Не было проверено, существуют ли какие-либо неоткрытые простые числа Мерсенна между 48-м ( M 57 885 161 ) и 51-м ( M 82 589 933 ) в этой таблице; поэтому рейтинг является предварительным.
  7. ^ M 74 207 281 впервые был отправлен в GIMPS 17 сентября 2015 г., но не был замечен человеком до 7 января 2016 г. из-за ошибки сервера.

Ссылки [ править ]

  1. ^ Перейти обратно: а б Стиллвелл, Джон (2010). Математика и ее история . Тексты для бакалавриата по математике. Springer Science+Business Media . п. 40. ИСБН  978-1-4419-6052-8 . Архивировано из оригинала 13 октября 2021 года . Проверено 13 октября 2021 г.
  2. ^ Перейти обратно: а б с д Это ж г Колдуэлл, Крис К. «Простые числа Мерсенна: история, теоремы и списки» . ПраймПейджс . Архивировано из оригинала 4 октября 2021 года . Проверено 4 октября 2021 г.
  3. ^ Колдуэлл, Крис К. «Если 2 н -1 является простым, то и n" . PrimePages . Архивировано из оригинала 5 октября 2021 года . Проверено 12 октября 2021 года .
  4. ^ Приепп, Роберт В. (1970). «Совершенные числа, многочисленные числа и недостаточные числа» . Учитель математики . 63 (8): 692–96. дои : 10.5951/MT.63.8.0692 . JSTOR   27958492 . Архивировано из оригинала 5 октября 2021 года . Проверено 13 октября 2021 г. - через JSTOR.
  5. ^ Колдуэлл, Крис К. «Охарактеризация всех даже совершенных чисел» . ПраймПейджс . Архивировано из оригинала 8 октября 2014 года . Проверено 12 октября 2021 г.
  6. ^ Перейти обратно: а б Крилли, Тони (2007). «Идеальные числа». 50 математических идей, которые вам действительно нужно знать . Издательство Кверкус. ISBN  978-1-84724-008-8 . Архивировано из оригинала 13 октября 2021 года . Проверено 13 октября 2021 г.
  7. ^ Колдуэлл, Крис К. «Эвристическая модель распределения Мерсенна» . ПраймПейджс . Архивировано из оригинала 5 октября 2021 года . Проверено 13 октября 2021 г.
  8. ^ Вагстафф, Сэмюэл С. (январь 1983 г.). «Делители чисел Мерсенна» . Математика вычислений . 40 (161): 385–397. doi : 10.1090/S0025-5718-1983-0679454-X . ISSN   0025-5718 .
  9. ^ Померанс, Карл (сентябрь 1981 г.). «Последние разработки в области тестирования простоты» (PDF) . Математический интеллект . 3 (3): 97–105. дои : 10.1007/BF03022861 . ISSN   0343-6993 . S2CID   121750836 .
  10. ^ Охем, Паскаль; Рао, Микаэль (30 января 2012 г.). «Нечетные совершенные числа больше 10». 1500 " . Математика вычислений . 81 (279): 1869–1877. doi : 10.1090/S0025-5718-2012-02563-4 . ISSN   0025-5718 .
  11. ^ Перейти обратно: а б «Отчет об основных этапах работы GIMPS» . Отличный поиск простых чисел Мерсенна в Интернете . Архивировано из оригинала 13 октября 2021 года . Проверено 31 января 2024 г.
  12. ^ Источники, относящиеся почти ко всем записям:
  13. ^ Перейти обратно: а б с д Джойс, Дэвид Э. «Элементы Евклида, Книга IX, Предложение 36» . mathcs.clarku.edu . Архивировано из оригинала 17 июня 2021 года . Проверено 13 октября 2021 г.
  14. ^ Перейти обратно: а б с д Это ж Диксон, Леонард Юджин (1919). История теории чисел, Том. Я. ​ Институт Карнеги в Вашингтоне. стр. 4–6. Архивировано из оригинала 8 апреля 2023 г. Проверено 19 марта 2023 г.
  15. ^ Перейти обратно: а б с д Это Смит, Дэвид Юджин (1925). История математики: Том II . Дувр. п. 21. ISBN  978-0-486-20430-7 .
  16. ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Совершенные числа» . MacTutor Архив истории математики . Архивировано из оригинала 5 октября 2021 года . Проверено 13 октября 2021 г.
  17. ^ « 'Calendarium ecclesiasticum – BSB Clm 14908' » . Баварская государственная библиотека . Архивировано из оригинала 13 октября 2021 года . Проверено 13 октября 2021 г.
  18. ^ Перейти обратно: а б Катальди, Пьетро Антонио (1603). Трактат о совершенных числах Пьетро Антонио Катальдо [ Трактат Пьетро Антонио Катальди о совершенных числах ] (на итальянском языке). «В Эреди», Джоуанни Росси. Архивировано из оригинала 5 апреля 2023 г. Проверено 19 марта 2023 г.
  19. ^ Колдуэлл, Крис К. «Модульные ограничения на делители Мерсенна» . ПраймПейджс . Архивировано из оригинала 11 ноября 2021 года . Проверено 22 ноября 2021 г.
  20. ^ Эйлер, Леонард (1772). «Отрывок из письма г-на Эйлера г-ну Бернулли по поводу мемуаров, опубликованных среди мемуаров 1771 года , стр. 318» ]. Новые мемуары Королевской академии наук Берлина (на французском языке). 1772 : 35–36. Архивировано из оригинала 15 августа 2020 года . Получено 13 октября 2021 г. - из Архива Эйлера.
  21. ^ «О новом простом числе, объявленном Первошиным] . Вестник Императорской Академии наук Санкт-Петербурга (на французском языке). 31 : 532–533. 27 января 1887 года. Архивировано из оригинала 13 октября 2021 года . Получено 13 октября 2021 г. - из Библиотеки наследия биоразнообразия .
  22. ^ Пауэрс, RE (ноябрь 1911 г.). «Десятое совершенное число». Американский математический ежемесячник . 18 (11): 195–197. дои : 10.2307/2972574 . JSTOR   2972574 .
  23. ^ «Протоколы заседаний». Труды Лондонского математического общества . с2-13 (1): iv–xl. 1914. дои : 10.1112/plms/s2-13.1.1-s .
  24. ^ Лукас, Эдвард (1876). «Заметка о применении рекуррентных рядов к исследованию закона распределения простых чисел ». Труды Академии наук (на французском языке). 82 : 165–167. Архивировано из оригинала 13 октября 2021 года . Проверено 13 октября 2021 г.
  25. ^ Перейти обратно: а б "Примечания" . Математика вычислений . 6 (37): 58–61. Январь 1952 г. doi : 10.1090/S0025-5718-52-99405-2 . ISSN   0025-5718 . Архивировано из оригинала 13 октября 2021 года . Проверено 13 октября 2021 г.
  26. ^ "Примечания" . Математика вычислений . 6 (39): 204–205. Июль 1952 г. doi : 10.1090/S0025-5718-52-99389-7 . ISSN   0025-5718 .
  27. ^ Перейти обратно: а б "Примечания" . Математика вычислений . 7 (41): 67–72. Январь 1953 г. doi : 10.1090/S0025-5718-53-99372-7 . ISSN   0025-5718 .
  28. ^ Ризель, Ганс (январь 1958 г.). «Новое простое число Мерсенна» . Математика вычислений . 12 (61): 60. дои : 10.1090/S0025-5718-58-99282-2 . Архивировано из оригинала 28 октября 2021 г. Проверено 13 октября 2021 г.
  29. ^ Перейти обратно: а б Гурвиц, Александр (апрель 1962 г.). «Новые простые числа Мерсенна» . Математика вычислений . 16 (78): 249–251. doi : 10.1090/S0025-5718-1962-0146162-X . ISSN   0025-5718 .
  30. ^ Перейти обратно: а б с Гиллис, Дональд Б. (январь 1964 г.). «Три новых простых числа Мерсенна и статистическая теория» . Математика вычислений . 18 (85): 93–97. дои : 10.1090/S0025-5718-1964-0159774-6 . JSTOR   2003409 .
  31. ^ Такерман, Брайант (октябрь 1971 г.). «24-е число Мерсенна» . Труды Национальной академии наук . 68 (10): 2319–2320. Бибкод : 1971PNAS...68.2319T . дои : 10.1073/pnas.68.10.2319 . ПМК   389411 . ПМИД   16591945 .
  32. ^ Перейти обратно: а б Нолл, Лэндон Курт ; Никель, Лаура (октябрь 1980 г.). «25-е и 26-е простые числа Мерсенна» . Математика вычислений . 35 (152): 1387. doi : 10.1090/S0025-5718-1980-0583517-4 . JSTOR   2006405 .
  33. ^ Словински, Дэвид (1978). «В поисках 27-го простого числа Мерсенна». Журнал развлекательной математики . 11 (4): 258–261.
  34. ^ «Научные часы: новое простое число» . Нью-Йорк Таймс . 5 июня 1979 года. Архивировано из оригинала 2 ноября 2021 года . Проверено 13 октября 2021 г.
  35. ^ «Объявления» . Математический интеллект . 5 (1): 60. Март 1983 г. doi : 10.1007/BF03023507 . ISSN   0343-6993 .
  36. ^ Петерсон, И. (6 февраля 1988 г.). «Готовность к удачному удару». Новости науки . 133 (6): 85. дои : 10.2307/3972461 . JSTOR   3972461 .
  37. ^ Колкитт, Западная Нью-Йорк; Уэлш, Л. (апрель 1991 г.). «Новое простое число Мерсенна» . Математика вычислений . 56 (194): 867. Бибкод : 1991MaCom..56..867C . дои : 10.1090/S0025-5718-1991-1068823-9 . JSTOR   2008415 .
  38. ^ «Число — это самое большое простое число, найденное на данный момент» . Глобус и почта . 24 сентября 1983 года. ПроКвест   386439660 . Архивировано из оригинала 2 ноября 2021 года . Проверено 7 января 2022 г. - через ProQuest .
  39. ^ Петерсон, И. (28 сентября 1985 г.). «Прайм-тайм для суперкомпьютеров». Новости науки . 128 (13): 199. дои : 10.2307/3970245 . JSTOR   3970245 .
  40. ^ Дембарт, Ли (17 сентября 1985 г.). «Суперкомпьютер выдал колоссальное простое число» . Лос-Анджелес Таймс . Архивировано из оригинала 2 ноября 2021 года . Проверено 13 октября 2021 г.
  41. ^ Мэддокс, Джон (26 марта 1992 г.). «Бесконечный поиск первобытности» . Природа . 356 (6367): 283. Бибкод : 1992Natur.356..283M . дои : 10.1038/356283a0 . ISSN   1476-4687 . S2CID   4327045 .
  42. ^ «Самое большое известное простое число обнаружено на суперкомпьютере Cray Research» . Пиар-новости . 10 января 1994 года. Архивировано из оригинала 4 ноября 2021 года . Проверено 21 августа 2023 г. - через Гейла .
  43. ^ Колдуэлл, Крис К. «Простое число рекордного размера! 2» 1257787 -1" . PrimePages . Архивировано из оригинала 5 октября 2021 года . Проверено 13 октября 2021 года .
  44. ^ Гиллмор, Дэн (3 сентября 1996 г.). «Пересчет чисел: исследователи сделали открытие в области первичной математики» . Найт Риддер – через Гейла .
  45. ^ «ГИМПС обнаруживает 35-е число Мерсенна, 2». 1,398,269 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 12 ноября 1996 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  46. ^ «GIMPS обнаруживает 36-е число простого числа Мерсенна, 2». 2,976,221 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 1 сентября 1997 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  47. ^ «ГИМПС обнаруживает 37-е число Мерсенна, 2 3,021,377 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 2 февраля 1998 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  48. ^ «GIMPS обнаружил 38-е число Мерсенна Прайм 2». 6,972,593 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 30 июня 1999 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  49. ^ «ГИМПС обнаруживает 39-е число Мерсенна-Прайм, 2». 13,466,917 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 6 декабря 2001 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  50. ^ «ГИМПС обнаруживает 40-е простое число Мерсенна, 2». 20,996,011 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 2 февраля 2003 г. Архивировано из оригинала 7 июня 2020 г. Проверено 13 октября 2021 г.
  51. ^ «ГИМПС обнаруживает 41-е число Мерсенна-Прайм, 2». 24,036,583 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 28 мая 2004 г. Архивировано из оригинала 29 января 2021 г. Проверено 13 октября 2021 г.
  52. ^ «GIMPS обнаруживает 42-й номер Мерсенна-Прайм, 2». 25,964,951 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 27 февраля 2005 г. Архивировано из оригинала 14 марта 2021 г. Проверено 13 октября 2021 г.
  53. ^ «ГИМПС обнаруживает 43-е число Мерсенна-Прайм, 2». 30,402,457 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 24 декабря 2005 г. Архивировано из оригинала 14 марта 2021 г. Проверено 13 октября 2021 г.
  54. ^ «ГИМПС обнаруживает 44-е число Мерсенна, 2». 32,582,657 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 11 сентября 2006 г. Архивировано из оригинала 26 января 2021 г. Проверено 13 октября 2021 г.
  55. ^ Перейти обратно: а б «GIMPS обнаружил 45-е и 46-е простые числа Мерсенна, 2 43,112,609 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 15 сентября 2008 г. Архивировано из оригинала 5 октября 2021 г. Проверено 13 октября 2021 г.
  56. ^ «ГИМПС обнаруживает 47-е простое число Мерсенна» . Отличный поиск простых чисел Мерсенна в Интернете . 12 апреля 2009 г. Архивировано из оригинала 19 февраля 2021 г. Проверено 13 октября 2021 г.
  57. ^ Мо, Томас Х. (27 сентября 2008 г.). «Найдено редкое простое число» . Лос-Анджелес Таймс . Архивировано из оригинала 27 июля 2021 года . Проверено 13 октября 2021 г.
  58. ^ Смит, Эдсон. «Калифорнийский университет в Лос-Анджелесе Мерсенн Прайм» . Математика Калифорнийского университета в Лос-Анджелесе . Архивировано из оригинала 22 ноября 2021 года . Проверено 22 ноября 2021 г.
  59. ^ «ГИМПС обнаруживает 48-е число простых чисел Мерсенна, 2». 57,885,161 -1 теперь является самым большим известным простым числом» . Отличный поиск простых чисел Мерсенна в Интернете . 5 февраля 2013 г. Архивировано из оригинала 26 января 2021 г. Проверено 13 октября 2021 г.
  60. ^ Йирка, Боб (6 февраля 2013 г.). «Профессор университета обнаружил самое большое на сегодняшний день простое число» . физ.орг . Архивировано из оригинала 16 января 2021 года . Проверено 13 октября 2021 г.
  61. ^ «Проект GIMPS обнаружил самое большое известное простое число: 2». 74,207,281 -1" . Отличный поиск простых чисел Мерсенна в Интернете . 19 января 2016. Архивировано из оригинала 7 января 2018 года . Проверено 13 октября 2021 года .
  62. ^ «Самое большое известное простое число обнаружено в Миссури» . Новости BBC . 20 января 2016 г. Архивировано из оригинала 21 августа 2021 г. Проверено 13 октября 2021 г.
  63. ^ «Проект GIMPS обнаружил самое большое известное простое число: 2». 77,232,917 -1" . Отличный интернет-поиск простых чисел Мерсенна . 3 января 2018. Архивировано из оригинала 4 января 2018 года . Проверено 13 октября 2021 года .
  64. ^ Лэмб, Эвелин (4 января 2018 г.). «Почему вас должно волновать простое число длиной 23 249 425 цифр» . Журнал «Сланец» . Архивировано из оригинала 9 октября 2021 года . Проверено 13 октября 2021 г.
  65. ^ «GIMPS обнаружил самое большое известное простое число: 2». 82,589,933 -1" . Отличный интернет-поиск простых чисел Мерсенна . 21 декабря 2018. Архивировано из оригинала 22 декабря 2018 года . Проверено 13 октября 2021 года .
  66. ^ Палка, Джо (21 декабря 2018 г.). «В мире появилось новое самое известное простое число» . ЭНЕРГЕТИЧЕСКИЙ ЯДЕРНЫЙ РЕАКТОР . Архивировано из оригинала 30 июля 2021 года . Проверено 13 октября 2021 г.

Внешние ссылки [ править ]

Retrieved from "https://en.wikipedia.org/w/index.php?title=List_of_Mersenne_primes_and_perfect_numbers&oldid=1227745325"
Arc.Ask3.Ru: конец оригинального документа.
Arc.Ask3.Ru
Номер скриншота №: BDC1043974C524C7B62DF1413EFD5812__1717763820
URL1:https://en.wikipedia.org/wiki/List_of_Mersenne_primes_and_perfect_numbers
Заголовок, (Title) документа по адресу, URL1:
List of Mersenne primes and perfect numbers - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть, любые претензии не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, денежную единицу можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)