ХСЛ и ВПГ

Рис. 1. HSL (а–г) и ВПГ (д–з). Вверху (a, e): 3D-модели каждого в разрезе. Внизу: двумерные графики, показывающие одновременно два из трех параметров модели, при этом второй остается постоянным: цилиндрические оболочки (b, f) постоянной насыщенности, в данном случае внешняя поверхность каждого цилиндра; горизонтальные сечения (c, g) постоянной светлоты HSL или значения HSV, в данном случае срезы посередине каждого цилиндра; и прямоугольные вертикальные сечения (d, h) постоянного оттенка, в данном случае красного цвета 0° и дополняющего его 180° голубого.

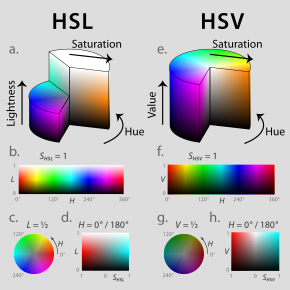
HSL и HSV — два наиболее распространенных цилиндрических координатах представления точек в в цветовой модели RGB . Эти два представления перестраивают геометрию RGB, пытаясь сделать их более интуитивными и воспринимаемыми , чем декартово (кубическое) представление. Разработанные в 1970-х годах для приложений компьютерной графики , HSL и HSV сегодня используются в средствах выбора цвета , в программном обеспечении для редактирования изображений и реже в анализе изображений и компьютерном зрении .

HSL означает оттенок , насыщенность и яркость и часто также называется HLS . HSV означает оттенок , насыщенность и значение , а также часто называется HSB ( B — яркость ). Третья модель, распространенная в приложениях компьютерного зрения, — это HSI , для оттенка , насыщенности и интенсивности . Однако, хотя эти определения обычно последовательны, они не стандартизированы, и любое из этих сокращений может использоваться для любой из этих трех или нескольких других связанных цилиндрических моделей. (Технические определения этих терминов см. ниже .)

В каждом цилиндре угол вокруг центральной вертикальной оси соответствует « оттенку », расстояние от оси соответствует « насыщенности », а расстояние по оси соответствует « яркости », «величине» или « яркости ». Обратите внимание: хотя «оттенок» в HSL и HSV относится к одному и тому же атрибуту, их определения «насыщенности» существенно различаются. Поскольку HSL и HSV представляют собой простые преобразования зависимых от устройства моделей RGB, определяемые ими физические цвета зависят от цветов красного, зеленого и синего основных цветов устройства или конкретного пространства RGB, а также от гамма-коррекции , используемой для представления суммы этих праймериз. Таким образом, каждое уникальное устройство RGB имеет уникальные пространства HSL и HSV, а числовые значения HSL или HSV описывают разные цвета для каждого базового пространства RGB.

Оба этих представления широко используются в компьютерной графике, и то или иное из них часто более удобно, чем RGB, но оба также подвергаются критике за недостаточное разделение цветовых атрибутов или за отсутствие единообразия восприятия. другие модели с более интенсивными вычислениями, такие как CIELAB или CIECAM02, Говорят, что лучше достигают этих целей.

Основной принцип

Рис. 2а. HSL-цилиндр.

Рис. 2б. цилиндр ВСВ.

HSL и HSV представляют собой цилиндрическую геометрию ( рис. 2 ), с оттенком, их угловым размером, начиная с красного основного элемента под углом 0°, проходя через зеленый основной элемент под углом 120° и синий основной элемент под углом 240°, а затем возвращаясь обратно к красный на 360°. В каждой геометрии центральная вертикальная ось содержит нейтральные , ахроматические или серые цвета в диапазоне сверху вниз от белого при яркости 1 (значение 1) до черного при яркости 0 (значение 0).

В обеих геометриях аддитивные первичные и вторичные цвета — красный, желтый , зеленый, голубой , синий и пурпурный — и линейные смеси между соседними парами из них, иногда называемые чистыми цветами , расположены вокруг внешнего края цилиндра с насыщенностью 1. Эти насыщенные цвета имеют яркость 0,5 в HSL, тогда как в HSV они имеют значение 1. Смешение этих чистых цветов с черным, создавая так называемые оттенки , оставляет насыщенность неизменной. В HSL насыщенность также не изменяется при окрашивании белым, и только смеси черного и белого цветов, называемые тонами , имеют насыщенность менее 1. В HSV только тонирование снижает насыщенность.

Рис. 3а–б. Если мы отобразим оттенок и (а) яркость HSL или (б) значение HSV в зависимости от цветности ( диапазон значений RGB), а не от насыщенности (цветность превышает максимальную цветность для этого среза), полученное твердое тело будет биконусом или конусом , соответственно, а не цилиндр. На таких диаграммах часто утверждается, что они представляют HSL или HSV напрямую, а измерение цветности ошибочно называют «насыщенностью».

Потому что эти определения насыщенности – при которых очень темные (в обеих моделях) или очень светлые (в HSL) почти нейтральные цвета считаются полностью насыщенными (например,   справа внизу в разрезанном цилиндре HSL или   справа вверху) – конфликтует с интуитивным представлением о чистоте цвета, часто коническое или биконическое вместо этого рисуется тело ( рис. 3 ), радиальное измерение которого в этой статье называется цветностью (равным диапазону значений RGB), а не насыщенностью (где насыщенность равна цветности максимальной цветности в этом срезе (би)конуса). Как ни странно, такие диаграммы обычно обозначают это радиальное измерение как «насыщенность», размывая или стирая различие между насыщенностью и цветностью. Как описано ниже , вычисление цветности является полезным шагом при создании каждой модели. Поскольку такая промежуточная модель - с размерами оттенка, цветности и значения HSV или светлоты HSL - принимает форму конуса или биконуса, HSV часто называют «моделью шестигранного конуса», а HSL часто называют «моделью бигексонуса» ( рис. 8 ).

Мотивация

См. также: Теория цвета , цветовая модель RGB и цветовое пространство RGB.

Рис. 4. Художники долго смешивали цвета, сочетая относительно яркие пигменты с черным и белым. Смеси с белым называются оттенками , смеси с черным — оттенками , а смеси с обоими — тонами . См. Оттенки и оттенки .

Рис. 5. Эта цветовая модель немецкого химика Вильгельма Оствальда 1916 года иллюстрирует подход «смеси с белым и черным», организуя 24 «чистых» цвета в цветовой круг , а цвета каждого оттенка в треугольник. Таким образом, модель принимает форму биконуса.

Рис. 6а. Гамму RGB можно расположить в кубе.

Рис. 6б. То же изображение, часть которого удалена для наглядности.

Рис. 7. В графических терминалах Tektronix использовалась самая ранняя коммерческая реализация HSL, в 1979 году. На этой диаграмме из патента, поданного в 1983 году, показана геометрия биконуса, лежащая в основе модели.

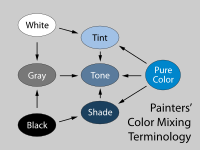
Большинство телевизоров, компьютерных дисплеев и проекторов воспроизводят цвета, комбинируя красный, зеленый и синий свет различной интенсивности — так называемые RGB аддитивные основные цвета . Получающиеся смеси в цветовом пространстве RGB могут воспроизводить самые разные цвета (называемые гаммой ); однако взаимосвязь между составляющими количествами красного, зеленого и синего света и полученным цветом неинтуитивна, особенно для неопытных пользователей, а также для пользователей, знакомых с субтрактивным смешением красок или традиционными моделями художников, основанными на оттенках и оттенках ( рис. . 4 ). Более того, ни аддитивные, ни субтрактивные цветовые модели не определяют цветовые отношения так же, как это делает человеческий глаз .

Например, представьте, что у нас есть RGB-дисплей, цвет которого контролируется тремя ползунками в диапазоне от 0 до 255 , один из которых управляет интенсивностью каждого из основных цветов: красного, зеленого и синего. Если мы начнем с относительно яркого оранжевого цвета   со sRGB значениями R = 217 , G = 118 , B = 33 и хотим уменьшить его красочность наполовину до менее насыщенного оранжевого цвета   , нам нужно будет перетащить ползунки, чтобы уменьшить R на 31. , увеличьте G на 24 и увеличьте B на 59, как показано ниже.

Начиная с 1950-х годов в цветном телевизионном вещании использовалась совместимая цветовая система, в которой сигналы « яркости » и « цветности » кодировались отдельно, так что существующие немодифицированные черно-белые телевизоры могли принимать цветные передачи и показывать монохромное изображение.

Пытаясь внедрить более традиционные и интуитивно понятные модели смешивания цветов, пионеры компьютерной графики из PARC и NYIT в середине 1970-х годов представили модель HSV для технологии компьютерных дисплеев, официально описанную Элви Рэем Смитом. в августовском номере журнала Computer Graphics за 1978 год . В том же номере Джолав и Гринберг описали модель HSL, размеры которой они обозначили оттенком , относительной насыщенностью и интенсивностью , и сравнили ее с HSV ( рис. 1 ). Их модель была основана больше на том, как цвета организуются и концептуализируются в человеческом зрении с точки зрения других цветообразующих атрибутов, таких как оттенок, яркость и насыщенность; а также традиционные методы смешивания цветов – например, в живописи – которые включают смешивание ярких пигментов с черным или белым для получения более светлых, темных или менее красочных цветов.

В следующем, 1979 году, на SIGGRAPH выставке компания Tektronix представила графические терминалы, использующие HSL для обозначения цвета, и Комитет по стандартам компьютерной графики рекомендовал это в своем ежегодном отчете о состоянии ( рис. 7 ). Эти модели были полезны не только потому, что они были более интуитивными, чем необработанные значения RGB, но и потому, что преобразования в RGB и обратно выполнялись чрезвычайно быстро: они могли выполняться в реальном времени на оборудовании 1970-х годов. Следовательно, с тех пор эти и подобные модели стали повсеместно использоваться в программном обеспечении для редактирования изображений и графики. Некоторые из их применений описаны ниже .

Формальный вывод

Рис. 8. Геометрический вывод цилиндрических представлений HSL и HSV «цветного куба» RGB.

Duration: 15 seconds.0:15

Визуализированное геометрическое происхождение цилиндрического представления HSV «цветного куба» RGB.

Duration: 15 seconds.0:15

Визуализированный геометрический вывод цилиндрического HSL-представления «цветного куба» RGB.

Цветообразующие атрибуты

См. Также: Цветовое зрение.

Размеры геометрий HSL и HSV — простые преобразования модели RGB, не основанной на восприятии — не связаны напрямую с фотометрическими одноимёнными атрибутами формирования цвета, как это определено такими учёными, как CIE или ASTM . Тем не менее, стоит просмотреть эти определения, прежде чем приступить к выводу наших моделей. Следующие ниже определения атрибутов создания цвета см.:

Хюэ

«Атрибут зрительного ощущения, согласно которому область кажется похожей на один из воспринимаемых цветов : красный, желтый, зеленый и синий или на комбинацию двух из них».

Сияние ( L _{e, Ом} )

Излучающая сила света, проходящего через определенную поверхность на единицу телесного угла на единицу проецируемой площади, измеряется в единицах СИ , в ваттах на стерадиан на квадратный метр ( Вт·ср). ⁻¹ ·м ⁻² ).

Яркость ( Y или L _{v, Ом} )

Излучение, взвешенное по влиянию каждой длины волны на типичного человека-наблюдателя, измеренное в единицах СИ в канделах на квадратный метр ( кд/м). ² ). Часто термин яркость используется для обозначения яркости относительной Y / Y _n , где Y _n — яркость эталонной точки белого .

Лума ( Y ′ )

Взвешенная сумма гамма-скорректированных значений R ′ , G ′ и B ′ , используемая в Y ′ CbCr для сжатия JPEG и передачи видео.

Яркость (или значение)

«Атрибут зрительного ощущения, согласно которому область излучает больше или меньше света».

Легкость

«Яркость относительно яркости аналогично освещенного белого цвета».

Красочность

«Атрибут зрительного ощущения, согласно которому воспринимаемый цвет области кажется более или менее хроматическим».

Цветность

«Красочность относительно яркости аналогично освещенного белого цвета».

Насыщенность

«Красочность стимула относительно его собственной яркости».

Яркость и цветность являются абсолютными мерами, которые обычно описывают спектральное распределение света, попадающего в глаз, тогда как яркость и цветность измеряются относительно некоторой точки белого и поэтому часто используются для описания цветов поверхности, оставаясь примерно постоянными, даже если яркость и красочность изменить с различным освещением . Насыщенность можно определить либо как соотношение красочности и яркости, либо как соотношение цветности и светлоты.

Общий подход

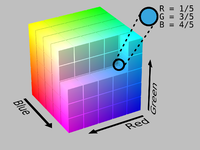
HSL, HSV и связанные с ними модели могут быть получены с помощью геометрических стратегий или могут рассматриваться как конкретные примеры «обобщенной модели LHS». Разработчики моделей HSL и HSV взяли куб RGB – с составляющими количествами красного, зеленого и синего света в цвете, обозначенном R , G , B ∈ [0, 1] — и наклонил его в углу так, чтобы черный находился в начале координат, а белый — прямо над ним вдоль вертикальной оси, затем измерил оттенок цветов в кубе по их углу вокруг этой оси, начиная с красного с 0 °. Затем они придумали характеристику яркости/значения/яркости и определили насыщенность в диапазоне от 0 по оси до 1 в самой красочной точке для каждой пары других параметров.

Оттенок и цветность

См. также: Оттенок и цветность.

Рис. 9. И оттенок, и цветность определяются на основе проекции куба RGB на шестиугольник в «плоскости цветности». Цветность — это относительный размер шестиугольника, проходящего через точку, а оттенок — насколько далеко от края этого шестиугольника находится точка.

В каждой из наших моделей мы рассчитываем как оттенок , так и то, что в этой статье будет называться цветностью , по Джоблаву и Гринбергу (1978), одинаковым способом – то есть оттенок цвета имеет одинаковые числовые значения во всех этих моделях. как и его цветность. Если мы возьмем наш наклоненный куб RGB и спроецируем его на « плоскость цветности », перпендикулярную нейтральной оси, наша проекция примет форму шестиугольника с красным, желтым, зеленым, голубым, синим и пурпурным в его углах ( рис. . 9 ). Оттенок — это примерно угол вектора к точке проекции, при этом красный равен 0 °, а цветность — это примерно расстояние точки от начала координат.

Точнее, и оттенок, и цветность в этой модели определяются относительно шестиугольной формы проекции. Цветность — это пропорция расстояния от начала координат до края шестиугольника. В нижней части соседней диаграммы это соотношение длин OP / OP ′ или, альтернативно, соотношение радиусов двух шестиугольников. Это соотношение представляет собой разницу между наибольшим и наименьшим значениями R , G или B в цвете. Чтобы упростить написание наших определений, мы определим эти максимальные, минимальные значения и значения компонентов цветности как M , m и C соответственно.

$M=\max(R,G,B)$

$m=\min(R,G,B)$

$C=\operatorname {range} (R,G,B)=M-m$

Чтобы понять, почему цветность можно записать как M − m , обратите внимание, что любой нейтральный цвет с R = G = B проецируется на начало координат и поэтому имеет 0 цветности. Таким образом, если мы добавим или вычтем одну и ту же величину из всех трех R , G и B , мы переместимся вертикально внутри нашего наклоненного куба и не изменим проекцию. Следовательно, любые два цвета ( R , G , B ) и ( R − m , G − m , B − m ) проецируются в одну и ту же точку и имеют одинаковую цветность. Цветность цвета, у которого один из компонентов равен нулю ( m = 0), представляет собой просто максимум двух других компонентов. Эта цветность равна M в частном случае цвета с нулевой компонентой и M − m вообще.

Оттенок [ — это доля расстояния вокруг края шестиугольника, проходящего через проецируемую точку, первоначально измеряемая в диапазоне 0, 1], но теперь обычно измеряемая в градусах [0°, 360°) . Для точек, которые проецируются на начало координат в плоскости цветности (т. е. серые), оттенок не определен. Математически это определение оттенка записывается по частям :

$H'={\begin{cases}\mathrm {undefined} ,&{\text{if }}C=0\\{\frac {G-B}{C}}{\bmod {6}},&{\text{if }}M=R\\{\frac {B-R}{C}}+2,&{\text{if }}M=G\\{\frac {R-G}{C}}+4,&{\text{if }}M=B\end{cases}}$

$H=60^{\circ }\times H'$

Иногда нейтральным цветам (т. е. с C = 0 ) для удобства представления присваивается оттенок 0°.

Рис. 10. Определения оттенка и цветности в HSL и HSV приводят к деформации шестиугольников в круги.

Эти определения представляют собой геометрическое преобразование шестиугольников в круги: каждая сторона шестиугольника линейно отображается на дуге круга в 60° ( рис. 10 ). После такого преобразования оттенок — это угол вокруг начала координат, а цветность — расстояние от начала координат: угол и величина вектора, указывающего на цвет.

Рис. 11. Построение прямоугольных координат цветности α и β , а затем преобразование их в оттенок H ₂ и цветность C ₂ дает немного другие значения, чем вычисление шестиугольного оттенка H и цветности C : сравните числа на этой диаграмме с числами, указанными ранее в этом разделе.

Иногда в приложениях анализа изображений это преобразование шестиугольника в круг пропускается, а оттенок и цветность (мы обозначим их H ₂ и C ₂ ) определяются обычными преобразованиями декартовых координат в полярные ( рис. 11 ). Самый простой способ получить их — использовать пару декартовых координат цветности, которые мы назовем α и β :

$\alpha =R-G\cdot \cos(60^{\circ })-B\cdot \cos(60^{\circ })={\tfrac {1}{2}}(2R-G-B)$

$\beta =G\cdot \sin(60^{\circ })-B\cdot \sin(60^{\circ })={\tfrac {\sqrt {3}}{2}}(G-B)$

$H_{2}=\operatorname {atan2} (\beta ,\alpha )$

$C_{2}=\operatorname {gmean} (\alpha ,\beta )={\sqrt {\alpha ^{2}+\beta ^{2}}}$

( Функция atan2 , «арктангенс с двумя аргументами», вычисляет угол по декартовой паре координат.)

Обратите внимание, что эти два определения оттенка ( H и H ₂ ) почти совпадают, с максимальной разницей между ними для любого цвета около 1,12° – которая возникает при двенадцати конкретных оттенках, например H = 13,38° , H ₂ = 12,26° – и с H = H ₂ для каждого угла, кратного 30°. Два определения цветности ( C и C ₂ ) различаются более существенно: они равны в углах нашего шестиугольника, но в точках на полпути между двумя углами, например H = H ₂ = 30° , мы имеем C = 1 , но ${\textstyle C_{2}={\sqrt {\frac {3}{4}}}\approx 0.866,}$ разница около 13,4%.

Легкость

Рис. 12а–г. Четыре различных возможных измерения «яркости», нанесенные на график в зависимости от цветности, для пары дополнительных оттенков. Каждый график представляет собой вертикальное сечение трехмерного цветного тела.

Хотя определение оттенка относительно непротиворечиво – оно примерно удовлетворяет критерию, согласно которому цвета одного и того же воспринимаемого оттенка должны иметь один и тот же числовой оттенок – определение измерения яркости или значения менее очевидно: существует несколько возможностей в зависимости от цели и задач. представительства. Вот четыре наиболее распространенных ( рис. 12 ; три из них также показаны на рис. 8 ):

• Простейшим определением является среднее арифметическое , то есть среднее значение трех компонентов, называемых в модели HSI интенсивностью ( рис. 12а ). Это просто проекция точки на нейтральную ось – вертикальная высота точки в нашем наклоненном кубе. Преимущество состоит в том, что вместе с расчетами оттенка и цветности на евклидовом расстоянии это представление сохраняет расстояния и углы из геометрии куба RGB.

  $I=\operatorname {avg} (R,G,B)={\tfrac {1}{3}}(R+G+B)$

• В модели «шестиугольника» HSV значение определяется как наибольшая компонента цвета, наша M выше ( рис. 12b ). При этом все три основных цвета, а также все «вторичные цвета» — голубой, желтый и пурпурный — помещаются в плоскость с белым, образуя шестиугольную пирамиду из куба RGB.

  $V=\max(R,G,B)=M$

• В модели HSL «бигексон» яркость определяется как среднее значение наибольшего и наименьшего цветовых компонентов ( рис. 12c ), т.е. средний диапазон компонентов RGB. Это определение также помещает первичные и вторичные цвета в плоскость, но плоскость, находящуюся посередине между белым и черным. Полученное цветное тело представляет собой двойной конус, похожий на конус Оствальда, показанный выше .

  $L=\operatorname {mid} (R,G,B)={\tfrac {1}{2}}(M+m)$

• Более значимая для восприятия альтернатива — использовать яркость ′ Y . в качестве измерения яркости ( рис. 12d ) Яркость — это средневзвешенное значение гамма-скорректированных R , G и B , основанное на их вкладе в воспринимаемую яркость, долгое время используемое в качестве монохроматического измерения в цветном телевещании. Для sRGB Rec . 709 основных цветов дают Y ′ ₇₀₉ , цифровой NTSC использует Y ′ ₆₀₁ в соответствии с Rec. 601 и некоторые другие основные цвета также используются, что приводит к получению разных коэффициентов.

  $Y'_{\text{601}}=0.299\cdot R+0.587\cdot G+0.114\cdot B$ (SDTV)

  $Y'_{\text{240}}=0.212\cdot R+0.701\cdot G+0.087\cdot B$ (Адобе)

  $Y'_{\text{709}}=0.2126\cdot R+0.7152\cdot G+0.0722\cdot B$ (ТВЧ)

  $Y'_{\text{2020}}=0.2627\cdot R+0.6780\cdot G+0.0593\cdot B$ (СВЧТВ, HDR)

Все четыре из них оставляют нейтральную ось в покое. То есть для цветов с R = G = B равную значению R , G или B. любая из четырех формулировок дает яркость ,

Графическое сравнение см. на рис. 13 ниже .

Насыщенность

Рис. 14а–г. И в HSL, и в HSV насыщенность — это просто цветность, масштабированная для заполнения интервала [0, 1] для каждой комбинации оттенка и яркости или значения.

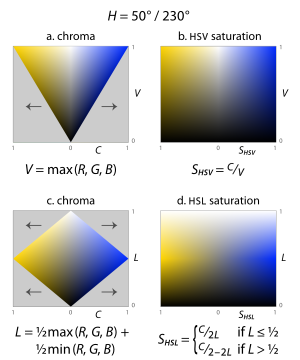
При кодировании цветов в модели оттенок/яркость/цветность или оттенок/значение/цветность (с использованием определений из двух предыдущих разделов) не все комбинации яркости (или значения) и цветности имеют смысл: то есть половина обозначаемых цветов при использовании H ∈ [0°, 360°) , C ∈ [0, 1] и V ∈ [0, 1] выходят за пределы гаммы RGB (серые части срезов на рисунке 14). Создатели этих моделей посчитали это проблемой для некоторых применений. Например, в интерфейсе выбора цвета, где два размера расположены в прямоугольнике, а третий — на ползунке, половина этого прямоугольника состоит из неиспользуемого пространства. Теперь представьте, что у нас есть ползунок яркости: намерение пользователя при настройке этого ползунка потенциально неоднозначно: как программа должна обрабатывать цвета, выходящие за пределы гаммы? Или наоборот, если пользователь выбрал как можно более красочный темно-фиолетовый цвет   , а затем сдвигает ползунок яркости вверх, что следует сделать: предпочел бы пользователь видеть более светлый фиолетовый цвет, но при этом максимально красочный для заданного оттенка и светлоты?  или более светло-фиолетовый, точно такой же насыщенности, как и исходный цвет   ?

Чтобы решить подобные проблемы, модели HSL и HSV масштабируют цветность так, чтобы она всегда вписывалась в диапазон [0, 1] новый атрибут насыщенности для каждой комбинации оттенка и яркости или значения, вызывая в обоих случаях (рис. 14). ). Чтобы рассчитать и то, и другое, просто разделите цветность на максимальную цветность для этого значения или яркости.

$S_{V}={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

$S_{L}={\begin{cases}0,&{\text{if }}L=1{\text{ or }}L=0\\{\frac {C}{1-|2L-1|}},&{\text{otherwise}}\end{cases}}$

Рис. 15а–б. В HSI насыщенность , показанная на срезе справа, примерно соответствует цветности относительно яркости. распространена модель с размерами , H2 , _I C2 , _Также показанная на срезе слева. Обратите внимание, что оттенок на этих срезах такой же, как и оттенок выше, но H немного отличается от H ₂ .

Модель HSI, обычно используемая для компьютерного зрения, которая принимает H ₂ в качестве измерения оттенка, а среднее значение компонента I («интенсивность») в качестве измерения яркости, не пытается «заполнить» цилиндр по определению насыщенности. Вместо предоставления конечным пользователям интерфейсов выбора цвета или модификации, цель HSI — облегчить разделение фигур на изображении. Таким образом, насыщенность определяется в соответствии с психометрическим определением: цветность относительно светлоты ( рис. 15 ). См. раздел «Использование при анализе изображений» этой статьи.

$S_{I}={\begin{cases}0,&{\text{if }}I=0\\1-{\frac {m}{I}},&{\text{otherwise}}\end{cases}}$

Использование одного и того же имени для этих трех разных определений насыщенности приводит к некоторой путанице, поскольку эти три атрибута описывают существенно разные цветовые отношения; в HSV и HSI этот термин примерно соответствует психометрическому определению насыщенности цвета относительно его собственной светлоты, но в HSL он и близко не приближается. Хуже того, слово «насыщенность» также часто используется для одного из измерений, которые мы выше называем цветностью ( C или C ₂ ).

Примеры

Все значения параметров, показанные ниже, даны как значения в интервале [0, 1] , за исключением значений H и H ₂ , которые находятся в интервале [0°, 360°) .

Цвет	Р	Г	Б	ЧАС	Ч 2	С	С 2	V	л	я	и ' 601	С ВПГ	С ХСЛ	С ХСИ
#FFFFFF	1.000	1.000	1.000	н/д	н/д	0.000	0.000	1.000	1.000	1.000	1.000	0.000	0.000	0.000
#808080	0.500	0.500	0.500	н/д	н/д	0.000	0.000	0.500	0.500	0.500	0.500	0.000	0.000	0.000
#000000	0.000	0.000	0.000	н/д	н/д	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
#FF0000	1.000	0.000	0.000	0.0 °	0.0 °	1.000	1.000	1.000	0.500	0.333	0.299	1.000	1.000	1.000
#BFBF00	0.750	0.750	0.000	60.0 °	60.0 °	0.750	0.750	0.750	0.375	0.500	0.664	1.000	1.000	1.000
#008000	0.000	0.500	0.000	120.0 °	120.0 °	0.500	0.500	0.500	0.250	0.167	0.293	1.000	1.000	1.000
#80FFFF	0.500	1.000	1.000	180.0 °	180.0 °	0.500	0.500	1.000	0.750	0.833	0.850	0.500	1.000	0.400
#8080FF	0.500	0.500	1.000	240.0 °	240.0 °	0.500	0.500	1.000	0.750	0.667	0.557	0.500	1.000	0.250
#BF40BF	0.750	0.250	0.750	300.0 °	300.0 °	0.500	0.500	0.750	0.500	0.583	0.457	0.667	0.500	0.571
#A0A424	0.628	0.643	0.142	61.8 °	61.5 °	0.501	0.494	0.643	0.393	0.471	0.581	0.779	0.638	0.699
#411БЕА	0.255	0.104	0.918	251.1 °	250.0 °	0.814	0.750	0.918	0.511	0.426	0.242	0.887	0.832	0.756
#1EAC41	0.116	0.675	0.255	134.9 °	133.8 °	0.559	0.504	0.675	0.396	0.349	0.460	0.828	0.707	0.667
#F0C80E	0.941	0.785	0.053	49.5 °	50.5 °	0.888	0.821	0.941	0.497	0.593	0.748	0.944	0.893	0.911
#B430E5	0.704	0.187	0.897	283.7 °	284.8 °	0.710	0.636	0.897	0.542	0.596	0.423	0.792	0.775	0.686
#ED7651	0.931	0.463	0.316	14.3 °	13.2 °	0.615	0.556	0.931	0.624	0.570	0.586	0.661	0.817	0.446
#FEF888	0.998	0.974	0.532	56.9 °	57.4 °	0.466	0.454	0.998	0.765	0.835	0.931	0.467	0.991	0.363
#19CB97	0.099	0.795	0.591	162.4 °	163.4 °	0.696	0.620	0.795	0.447	0.495	0.564	0.875	0.779	0.800
#362698	0.211	0.149	0.597	248.3 °	247.3 °	0.448	0.420	0.597	0.373	0.319	0.219	0.750	0.601	0.533
#7E7EB8	0.495	0.493	0.721	240.5 °	240.4 °	0.228	0.227	0.721	0.607	0.570	0.520	0.316	0.290	0.135

Использование в программном обеспечении конечного пользователя

См. также: Выбор цвета и редактирование изображений.

Рис. 16а–ж. К 1990-м годам инструменты выбора цвета HSL и HSV стали повсеместно распространены. Скриншоты выше взяты отсюда:

1. СГИ ИРИКС 5, гр. 1995 год ;
2. Adobe Photoshop , c. 1990 год ;
3. IBM OS/2 Warp 3, c. 1994 год ;
4. Apple Macintosh Система 7 , c. 1996 год ;
5. фрактал-дизайнер Художник- , ок. 1993 год ;
6. Microsoft Windows 3.1 , c. 1992 год ;
7. NeXTSTEP , гр. 1995 .

Они, несомненно, основаны на более ранних примерах, восходящих к PARC и NYIT в середине 1970-х годов.

Первоначальное назначение HSL, HSV и подобных моделей, а также их наиболее распространенное в настоящее время применение — инструменты выбора цвета . В простейшем случае некоторые такие средства выбора цвета предоставляют три ползунка, по одному для каждого атрибута. Однако большинство из них отображают двумерный срез модели вместе с ползунком, управляющим отображением конкретного среза. Последний тип графического интерфейса демонстрирует большое разнообразие благодаря выбору цилиндров, шестиугольных призм или конусов/биконусов, которые предлагаются моделями (см. диаграмму вверху страницы ). Справа показаны несколько средств выбора цвета 1990-х годов, большинство из которых за это время практически не изменились: сегодня почти каждый компьютерный специалист по выбору цвета использует HSL или HSV, по крайней мере, в качестве опции. Некоторые более сложные варианты предназначены для выбора целых наборов цветов, основываясь на предложениях совместимых цветов на отношениях HSL или HSV между ними.

существуют предварительно упакованные средства выбора цвета с открытым исходным кодом Большинство веб-приложений, нуждающихся в выборе цвета, также основывают свои инструменты на HSL или HSV, а для большинства основных веб- интерфейсных платформ . Спецификация CSS 3 позволяет веб-авторам указывать цвета для своих страниц непосредственно с помощью координат HSL.

HSL и HSV иногда используются для определения градиентов для визуализации данных , например, на картах или медицинских изображениях. Например, популярная ГИС- программа ArcGIS исторически применяла настраиваемые градиенты на основе HSV к числовым географическим данным.

Рис. 17. Модификатор цвета xv на основе HSV.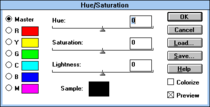

Рис. 18. Инструмент «Цветовой тон/Насыщенность» в Photoshop 2.5, ок. 1992.

Программное обеспечение для редактирования изображений также обычно включает инструменты для настройки цветов со ссылкой на координаты HSL или HSV или на координаты в модели на основе «интенсивности» или яркости, определенной выше . В частности, инструменты с парой ползунков «оттенок» и «насыщенность» являются обычным явлением, начиная с конца 1980-х годов, но также были реализованы различные более сложные инструменты цвета. Например, программа просмотра изображений Unix и редактор цвета xv размер шести определяемых пользователем диапазонов оттенков ( H позволяли поворачивать и изменять ), включали в себя циферблатный элемент управления насыщенностью ( S _HSV ) и интерфейс в виде кривых для управления значением ( В ) – см. рис. 17. Редактор изображений Picture Window Pro включает инструмент «цветокоррекции», который обеспечивает сложное переназначение точек в плоскости оттенка/насыщенности относительно пространства HSL или HSV.

Видеоредакторы также используют эти модели. Например, и Avid , и Final Cut Pro включают инструменты цвета на основе HSL или аналогичной геометрии для настройки цвета в видео. С помощью инструмента Avid пользователи выбирают вектор, щелкая точку внутри круга оттенка/насыщенности, чтобы сместить все цвета на определенный уровень яркости (тени, средние тона, светлые участки) на этот вектор.

слоев Adobe Photoshop «Яркость», «Оттенок», «Насыщенность» и «Цвет» Начиная с версии 4.0, режимы наложения составляют составные слои с использованием цветовой геометрии яркости/цветности/оттенка. Они широко копировались, но некоторые имитаторы вместо этого используют геометрию HSL (например, PhotoImpact , Paint Shop Pro ) или HSV.

Использование при анализе изображений

См. Также: Компьютерное зрение и анализ изображений.

HSL, HSV, HSI или родственные модели часто используются в компьютерном зрении и анализе изображений для обнаружения признаков или сегментации изображений . Приложения таких инструментов включают обнаружение объектов, например, в зрении робота ; распознавание объектов , например лиц , текста или номерных знаков ; поиск изображений на основе контента ; и анализ медицинских изображений .

По большей части алгоритмы компьютерного зрения, используемые для цветных изображений, представляют собой прямое расширение алгоритмов, разработанных для изображений в оттенках серого , например, k-средних или нечеткой кластеризации цветов пикселей или обнаружения скрытых границ . В самом простом случае каждый цветовой компонент отдельно проходит через один и тот же алгоритм. Поэтому важно, чтобы интересующие особенности можно было различить по используемым цветовым размерам. Поскольку компоненты R , G и B цвета объекта в цифровом изображении коррелируют с количеством света, падающего на объект, и, следовательно, друг с другом, описания изображения с точки зрения этих компонентов затрудняют различение объектов. Описания с точки зрения оттенка/яркости/цветности или оттенка/яркости/насыщенности часто более уместны.

Начиная с конца 1970-х годов такие преобразования, как HSV или HSI, использовались как компромисс между эффективностью сегментации и сложностью вычислений. Их можно рассматривать как схожие по подходу и назначению с нейронной обработкой, используемой человеческим цветовым зрением, не сходясь в деталях: если целью является обнаружение объекта, грубое разделение оттенка, яркости и цветности или насыщенности эффективно, но нет особая причина строго имитировать цветовую реакцию человека. В магистерской диссертации Джона Кендера 1976 года была предложена модель HSI. Охта и др. (1980) вместо этого использовали модель, состоящую из измерений, подобных тем, которые мы назвали I , α и β . В последние годы такие модели продолжают широко использоваться, поскольку их производительность выгодно отличается от более сложных моделей, а их вычислительная простота остается привлекательной.

Недостатки

Рис 20а. Гамма sRGB отображается в пространстве CIELAB. Обратите внимание, что линии, указывающие на основные цвета красного, зеленого и синего, расположены неравномерно по углу оттенка и имеют неравную длину. Первичные цвета также имеют разные значения L *.

Рис 20б. Гамма Adobe RGB отображается в пространстве CIELAB. Также обратите внимание, что эти два пространства RGB имеют разные гаммы и, следовательно, будут иметь разные представления HSL и HSV.

Хотя HSL, HSV и связанные с ними пространства служат достаточно хорошо, например, для выбора одного цвета, они игнорируют большую часть сложности внешнего вида цвета. По сути, они обменивают актуальность восприятия на скорость вычислений, начиная с того периода в истории вычислений (высокопроизводительные графические рабочие станции 1970-х годов или потребительские настольные компьютеры середины 1990-х годов), когда более сложные модели были бы слишком дорогими в вычислительном отношении.

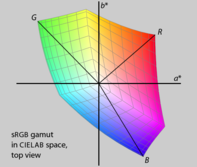
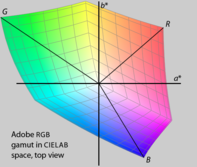
HSL и HSV — это простые преобразования RGB, которые сохраняют симметрию в кубе RGB, не связанную с человеческим восприятием, так что его углы R , G и B равноудалены от нейтральной оси и равномерно расположены вокруг нее. Если мы построим гамму RGB в более однородном для восприятия пространстве, таком как CIELAB (см. ниже ), сразу станет ясно, что основные цвета красного, зеленого и синего не имеют одинаковой яркости или цветности или равномерно расположенных оттенков. Более того, разные дисплеи RGB используют разные основные цвета и, следовательно, имеют разные гаммы. Поскольку HSL и HSV определяются исключительно со ссылкой на некоторое пространство RGB, они не являются абсолютными цветовыми пространствами : для точного указания цвета требуется сообщать не только значения HSL или HSV, но также характеристики пространства RGB, на котором они основаны, включая гамма-коррекция используется .

Если мы возьмем изображение и выделим компоненты оттенка, насыщенности и яркости или значения, а затем сравним их с одноименными компонентами, определенными учеными-цветовеками, мы сможем быстро увидеть разницу на уровне восприятия. Например, изучите следующие изображения огнедышащего ( рис. 13 ). Оригинал находится в цветовом пространстве sRGB. CIELAB L * — это определенная CIE величина ахроматической яркости (зависящая исключительно от воспринимаемой ахроматической яркости Y , но не от смешанных хроматических компонентов X или Z цветового пространства CIEXYZ, из которого получено само цветовое пространство sRGB), и она проста что по воспринимаемой легкости оно похоже на исходное цветное изображение. Яркость примерно похожа, но несколько отличается при высокой цветности, где она больше всего отклоняется от зависимости исключительно от истинной ахроматической яркости ( Y или, что эквивалентно, L *) и находится под влиянием колориметрической цветности ( x,y или, что эквивалентно, a*, б* CIELAB). HSL L и HSV V , напротив, существенно расходятся с перцептивной легкостью.

Рис. 13а. Цветная фотография (цветовое пространство sRGB).

Рис. 13б. CIELAB L * (дальнейшее преобразование обратно в sRGB для стабильного отображения).

Рис. 13в. Рек. 601 люма Y' .

Рис. 13г. Компонент средний: «интенсивность» I .

Рис. 13д. Значение V. HSV

Рис. 13е. HSL легкость L .

Рис 20в. 12 точек на цветовом круге HSV в плоскости цветности CIELAB , что указывает на отсутствие однородности HSV по оттенку и насыщенности.

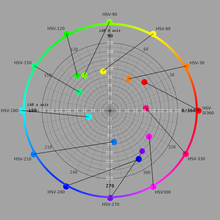
Хотя ни одно из измерений в этих пространствах не соответствует своим перцептивным аналогам, ценность HSV и насыщенность HSL являются особыми нарушениями. В HSV основной синий   и белый цвета   считаются имеющими одинаковое значение, даже несмотря на то, что воспринимаемый основной синий цвет имеет где-то около 10% яркости белого (точная доля зависит от конкретных используемых основных цветов RGB). В HSL смесь 100% красного, 100% зеленого и 90% синего, то есть очень светло-желтого цвета,   считается имеющей ту же насыщенность, что и основной зеленый цвет   , хотя первый цвет почти не имеет цветности или насыщенности. общепринятые психометрические определения. Подобные извращения побудили Синтию Брюэр, эксперта по выбору цветовой схемы для карт и информационных дисплеев, сообщить Американской статистической ассоциации :

Информатика предлагает несколько более бедных родственников этих пространств восприятия, которые также могут появиться в интерфейсе вашего программного обеспечения, например HSV и HLS. Это простые математические преобразования RGB, и они кажутся системами восприятия, поскольку используют терминологию оттенка-яркости/значения-насыщенности. Но посмотрите внимательно; не дайте себя обмануть. Перцептивные цветовые измерения плохо масштабируются цветовыми спецификациями, представленными в этих и некоторых других системах. Например, насыщенность и яркость путаются, поэтому шкала насыщенности может также содержать широкий диапазон значений яркости (например, она может прогрессировать от белого до зеленого, что представляет собой комбинацию яркости и насыщенности). Аналогично, оттенок и яркость путаются, так что, например, насыщенный желтый и насыщенный синий могут обозначаться как одна и та же «светота», но имеют большие различия в воспринимаемой легкости. Эти недостатки затрудняют использование систем для систематического управления внешним видом цветовой схемы. Если для достижения желаемого эффекта требуется значительная настройка, система не дает особых преимуществ по сравнению с необработанными спецификациями в RGB или CMY.

Если эти проблемы делают HSL и HSV проблематичными для выбора цветов или цветовых схем, они значительно ухудшают их настройку изображения. HSL и HSV, как упомянул Брюэр, смешивают перцептивные атрибуты формирования цвета, так что изменение любого измерения приводит к неравномерным изменениям во всех трех перцептивных измерениях и искажает все цветовые отношения в изображении. Например, вращение оттенка чистого темно-синего цвета   в сторону зеленого   также уменьшит его воспринимаемую цветность и увеличит воспринимаемую яркость (последний становится более серым и светлым), но такое же вращение оттенка будет иметь противоположное влияние на яркость и цветность цвета. более светлый голубовато-зеленый –   к   (последний более красочный и немного темнее). В примере ниже ( рис. 21 ) изображение (а) — это оригинальная фотография зеленой черепахи . На изображении (b) мы повернули оттенок ( H ) каждого цвета на -30° , сохранив при этом значение HSV и насыщенность или яркость и насыщенность HSL постоянными. На изображении справа (c) мы делаем такое же вращение для оттенка HSL/HSV каждого цвета, но затем форсируем яркость CIELAB ( L *, достойное приближение воспринимаемой легкости), чтобы оставаться постоянным. Обратите внимание, как средняя версия со смещением оттенка без такой коррекции резко меняет воспринимаемые отношения яркости между цветами на изображении. В частности, панцирь черепахи намного темнее и менее контрастен, а фоновая вода намного светлее. Изображение (d) использует CIELAB для изменения оттенка; отличие от (c) демонстрирует ошибки в оттенке и насыщенности.

Рис. 21а. Цветная фотография.

Рис. 21б. Оттенок HSL/HSV каждого цвета смещен на -30° .

Рис. 21в. Оттенок изменился, но яркость CIELAB ( L *) осталась такой же, как в оригинале.

Рис. 21г. Оттенок сдвинут в цветовом пространстве CIELch(ab) на −30° .

Поскольку оттенок представляет собой круговую величину, представленную численно с разрывом на 360°, его трудно использовать в статистических вычислениях или количественных сравнениях: анализ требует использования круговой статистики . Кроме того, оттенок определяется кусками, частями по 60°, где отношение яркости, значения и цветности к R , G и B зависит от рассматриваемого фрагмента оттенка. Это определение вводит разрывы, углы, которые можно ясно увидеть на горизонтальных срезах HSL или HSV.

Чарльз Пойнтон, эксперт по цифровому видео, перечисляет вышеупомянутые проблемы с HSL и HSV в своем FAQ по цвету и приходит к выводу, что:

HSB и HLS были разработаны для указания числового оттенка, насыщенности и яркости (или оттенка, яркости и насыщенности) в эпоху, когда пользователям приходилось указывать цвета в цифрах. Обычные формулировки HSB и HLS несовершенны в отношении свойств цветового зрения. Теперь, когда пользователи могут выбирать цвета визуально или выбирать цвета, связанные с другими медиа (например, PANTONE ), или использовать системы, основанные на восприятии, такие как L*u*v* и L*a*b* , от HSB и HLS следует отказаться.

Другие цветовые модели с цилиндрическими координатами

Основные статьи: Цветовая модель § Цветовые модели с цилиндрическими координатами и Список цветовых пространств и их использование § Цилиндрические преобразования.

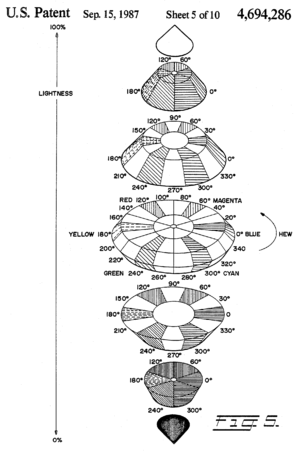
Создатели HSL и HSV были далеко не первыми, кто представил цвета, вписывающиеся в конические или сферические формы, с нейтральными оттенками, идущими от черного к белому по центральной оси, и оттенками, соответствующими углам вокруг этой оси. Подобные механизмы восходят к 18 веку и продолжают развиваться в самых современных и научных моделях.

Формулы преобразования цвета

Чтобы преобразовать HSL или HSV в RGB, мы по существу инвертируем шаги, перечисленные выше (как и раньше, R , G , B ∈ [0, 1] ). Сначала мы вычисляем цветность, умножая насыщенность на максимальную цветность для заданной яркости или значения. Затем мы находим точку на одной из трех нижних граней куба RGB, которая имеет тот же оттенок и насыщенность, что и наш цвет (и, следовательно, проецируется на ту же точку на плоскости цветности). Наконец, мы добавляем равное количество R , G и B, чтобы достичь нужной яркости или значения.

В RGB

HSL в RGB

цвет с оттенком H ∈ [0°, 360°) , насыщенностью SL _{Учитывая} ∈ [0, 1] и яркостью L ∈ [0, 1] , мы сначала находим цветность:

$C=(1-\left\vert 2L-1\right\vert )\times S_{L}$

Затем мы можем найти точку ( R ₁ , G ₁ , B ₁ ) вдоль трех нижних граней куба RGB с тем же оттенком и насыщенностью, что и наш цвет (используя промежуточное значение X для второго по величине компонента этого цвета). :

$H^{\prime }={\frac {H}{60^{\circ }}}$

$X=C\times (1-|H^{\prime }\;{\bmod {2}}-1|)$

В приведенном выше уравнении обозначение $H^{\prime }\;{\bmod {2}}$ относится к остатку евклидова деления $H^{\prime }$ на 2. $H^{\prime }$ не обязательно целое число.

$(R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$

Когда $H^{\prime }$ является целым числом, «соседняя» формула даст тот же результат, что и $X=0$ или $X=C$, по мере необходимости.

Наконец, мы можем найти R , G и B , добавив одинаковое количество к каждому компоненту, чтобы обеспечить яркость:

$m=L-{\frac {C}{2}}$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$

Альтернатива HSL-RGB

Полигональные кусочные функции можно несколько упростить за счет разумного использования минимальных и максимальных значений, а также операции с остатком.

Дан цвет с оттенком $H\in [0^{\circ },360^{\circ }]$, насыщенность $S=S_{L}\in [0,1]$и легкость $L\in [0,1]$, мы сначала определяем функцию:

$f(n)=L-a\max(-1,\min(k-3,9-k,1))$

где $k,n\in \mathbb {R} _{\geq 0}$ и:

$k=(n+{\frac {H}{30^{\circ }}}){\bmod {1}}2$

$a=S_{L}\min(L,1-L)$

И выведите значения R,G,B (из $[0,1]^{3}$) являются:

$(R,G,B)=(f(0),f(8),f(4))$

Вышеупомянутые альтернативные формулы допускают более короткие реализации. В приведенных выше формулах $a{\bmod {b}}$ операция также возвращает дробную часть модуля, например $7.4{\bmod {6}}=1.4$, и $k\in [0,12)$.

Базовая форма $T(k)=t(n,H)=\max(\min(k-3,9-k,1),-1)$ строится следующим образом: $t_{1}=\min(k-3,9-k)$ представляет собой «треугольник», для которого значения, большие или равные -1, начинаются с k=2 и заканчиваются на k=10, а самая высокая точка находится на k=6. Затем $t_{2}=\min(t_{1},1)=\min(k-3,9-k,1)$ мы меняем значения больше 1 на равные 1. Затем $t=\max(t_{2},-1)$ мы меняем значения меньше -1 на равные -1. На этом этапе мы получаем нечто похожее на красную фигуру на рис. 24 после вертикального переворота (где максимум равен 1, а минимум равен −1). Функции R,G,B $H$ используйте эту форму, преобразованную следующим образом: сдвинут по модулю на $X$ (к $n$) (по-другому для R,G,B) масштабируется по $Y$ (к $-a$) и перешел на $Y$ (к $L$).

Мы наблюдаем следующие свойства формы (рис. 24 может помочь получить представление о них):

$t(n,H)=-t(n+6,H)$

$\min \ (t(n,H),t(n+4,H),t(n+8,H))=-1$

$\max \ (t(n,H),t(n+4,H),t(n+8,H))=+1$

HSV в RGB

Рис. 24. Графическое представление координат RGB с учетом значений HSV. Это уравнение $V(1-S)=V-VS$ показывает происхождение отмеченных значений вертикальной оси.

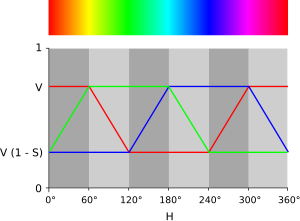
Учитывая цвет HSV с оттенком H € [0°, 360°) , насыщенностью S _V € [0, 1] и значением V € [0, 1] мы можем использовать ту же стратегию. Сначала находим цветность:

$C=V\times S_{V}$

Затем мы снова можем найти точку ( R ₁ , G ₁ , B ₁ ) вдоль трех нижних граней куба RGB с тем же оттенком и насыщенностью, что и наш цвет (используя промежуточное значение X для второго по величине компонента этот цвет):

$H^{\prime }={\frac {H}{60^{\circ }}}$

$X=C\times (1-|H^{\prime }{\bmod {2}}-1|)$

$(R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$

Как и прежде, когда $H^{\prime }$ является целым числом, «соседние» формулы дадут тот же результат.

Наконец, мы можем найти R , G и B , добавив одинаковое количество к каждому компоненту, чтобы получить соответствующее значение:

$m=V-C$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$

Альтернатива HSV вместо RGB

Дан цвет с оттенком $H\in [0^{\circ },360^{\circ }]$, насыщенность $S=S_{V}\in [0,1]$и значение $V\in [0,1]$сначала мы определяем функцию:

$f(n)=V-VS\max(0,\min(k,4-k,1))$

где $k,n\in \mathbb {R} _{\geq 0}$ и:

$k=(n+{\frac {H}{60^{\circ }}}){\bmod {6}}$

И выведите значения R,G,B (из $[0,1]^{3}$) являются:

$(R,G,B)=(f(5),f(3),f(1))$

Вышеуказанные альтернативные эквивалентные формулы допускают более короткую реализацию. В приведенных выше формулах $a{\bmod {b}}$ возвращает также дробную часть модуля, например формулу $7.4{\bmod {6}}=1.4$. Значения $k\in \mathbb {R} \land k\in [0,6)$. Базовая форма

$t(n,H)=T(k)=\max(0,\min(k,4-k,1))$

строится следующим образом: $t_{1}=\min(k,4-k)$ это «треугольник», для которого неотрицательные значения начинаются с k=0, наивысшая точка при k=2 и «заканчивается» при k=4, тогда мы меняем значения больше одного на один на $t_{2}=\min(t_{1},1)=\min(k,4-k,1)$, затем измените отрицательные значения на ноль с помощью $t=\max(t2,0)$ – и мы получаем (для $n=0$) что-то похожее на зеленую фигуру на рис. 24 (максимальное значение которого равно 1, а минимальное значение равно 0). Функции R,G,B $H$ используйте эту форму, преобразованную следующим образом: сдвинута по модулю на $X$ (к $n$) (по-другому для R,G,B) масштабируется по $Y$ (к $-VS$) и перешел на $Y$ (к $V$). Мы наблюдаем следующие свойства формы (рис. 24 может помочь получить представление об этом):

$t(n,H)=1-t(n+3,H)$

$\min(t(n,H),t(n+2,H),t(n+4,H))=0$

$\max(t(n,H),t(n+2,H),t(n+4,H))=1$

HSI в RGB

Учитывая цвет HSI с оттенком H € [0°, 360°) , насыщенностью S _I € [0, 1] и интенсивностью I € [0, 1] мы можем использовать ту же стратегию, но в немного другом порядке:

$H^{\prime }={\frac {H}{60^{\circ }}}$

$Z=1-|H^{\prime }\;{\bmod {2}}-1|$

$C={\frac {3\cdot I\cdot S_{I}}{1+Z}}$

$X=C\cdot Z$

Где $C$ это цветность.

Затем мы снова можем найти точку ( R ₁ , G ₁ , B ₁ ) вдоль трех нижних граней куба RGB с тем же оттенком и насыщенностью, что и наш цвет (используя промежуточное значение X для второго по величине компонента этот цвет):

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$

Перекрытие (когда $H^{\prime }$ является целым числом) возникает потому, что два способа вычисления значения эквивалентны: $X=0$ или $X=C$, по мере необходимости.

Наконец, мы можем найти R , G и B , добавив одинаковое количество к каждому компоненту, чтобы обеспечить яркость:

$m=I\cdot (1-S_{I})$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$

Яркость, цветность и оттенок в RGB

Учитывая цвет с оттенком H € [0°, 360°) , цветностью C € [0, 1] и яркостью Y ′ ₆₀₁ € [0, 1] , мы можем снова использовать ту же стратегию. уже есть и C , мы можем сразу найти нашу точку ( R1 _{Поскольку у} , G1 _нас , B1 _H ) вдоль трёх нижних граней куба RGB:

${\begin{aligned}H^{\prime }&={\frac {H}{60^{\circ }}}\\X&=C\times (1-|H^{\prime }{\bmod {2}}-1|)\end{aligned}}$

$(R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$

Перекрытие (когда $H^{\prime }$ является целым числом) возникает потому, что два способа вычисления значения эквивалентны: $X=0$ или $X=C$, по мере необходимости.

Затем мы можем найти R , G и B, добавив одинаковое количество к каждому компоненту, чтобы соответствовать яркости:

$m=Y_{601}^{\prime }-(0.30R_{1}+0.59G_{1}+0.11B_{1})$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$

Взаимная конверсия

HSV в HSL

Дан цвет с оттенком $H_{V}\in [0^{\circ },360^{\circ })$, насыщенность $S_{V}\in [0,1]$и значение $V\in [0,1]$,

$H_{L}=H_{V}$

$S_{L}={\begin{cases}0&{\text{if }}L=0{\text{ or }}L=1\\{\frac {V-L}{\min(L,1-L)}}&{\text{otherwise}}\\\end{cases}}$

$L=V\left(1-{\frac {S_{V}}{2}}\right)$

HSL в HSV

Дан цвет с оттенком $H_{L}\in [0^{\circ },360^{\circ })$, насыщенность $S_{L}\in [0,1]$и яркость $L\in [0,1]$,

$H_{V}=H_{L}$

$S_{V}={\begin{cases}0&{\text{if }}V=0\\2\left(1-{\frac {L}{V}}\right)&{\text{otherwise}}\\\end{cases}}$

$V=L+S_{L}\min(L,1-L)$

Из RGB

См. также: § Общий подход

Это повторение предыдущего преобразования.

Значение должно находиться в диапазоне $R,G,B\in [0,1]$.

С максимальным компонентом (т.е. значением)

$X_{\text{max}}:=\max(R,G,B)=:V$

и минимальный компонент

$X_{\text{min}}:=\min(R,G,B)=V-C$,

диапазон (т.е. цветность)

$C:=X_{\text{max}}-X_{\text{min}}=2(V-L)$

и средний диапазон (т.е. легкость)

$L:=\operatorname {mid} (R,G,B)={\frac {X_{\text{max}}+X_{\text{min}}}{2}}=V-{\frac {C}{2}}$,

мы получаем общий оттенок:

$H:={\begin{cases}0,&{\text{if }}C=0\\60^{\circ }\cdot \left({\frac {G-B}{C}}\mod 6\right),&{\text{if }}V=R\\60^{\circ }\cdot \left({\frac {B-R}{C}}+2\right),&{\text{if }}V=G\\60^{\circ }\cdot \left({\frac {R-G}{C}}+4\right),&{\text{if }}V=B\end{cases}}$

и отчетливые насыщенности:

$S_{V}:={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}$

$S_{L}:={\begin{cases}0,&{\text{if }}L=0{\text{ or }}L=1\\{\frac {C}{1-\left\vert 2V-C-1\right\vert }}={\frac {2(V-L)}{1-\left\vert 2L-1\right\vert }}={\frac {V-L}{\min(L,1-L)}},&{\text{otherwise}}\end{cases}}$

Образцы

Наведите указатель мыши на образцы ниже, чтобы увидеть значения R , G и B для каждого образца во всплывающей подсказке .

ХСЛ

Г = 180° Н = 0° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Н = 210° Н = 30° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
Г = 240° Н = 60° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Г = 270° В = 90° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
Н = 300° Г = 120° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Г = 330° Г = 150° Л \ С 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0

ВПГ

Г = 180° Н = 0° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Н = 210° Н = 30° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
Г = 240° Н = 60° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Г = 270° В = 90° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
Н = 300° Г = 120° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	Г = 330° Г = 150° V  \  S 1 3 ⁄ 4 1 ⁄ 2 1 ⁄ 4 0 1 ⁄ 4 1 ⁄ 2 3 ⁄ 4 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0

См. также

• Цветовая система Манселла
• Цветовое пространство TSL

Библиография

• Агостон, Макс К. (2005). Компьютерная графика и геометрическое моделирование: реализация и алгоритмы . Лондон: Спрингер. стр. 300–306. ISBN  978-1-85233-818-3 . Книга Агостона содержит описание HSV и HSL, а также алгоритмы в псевдокоде для преобразования в каждый из RGB и обратно.
• Ченг, Хэн-Да; Цзян, Сихуа; Сан, Анджела; Ван, Джингли (2001). «Сегментация цветного изображения: достижения и перспективы». Распознавание образов . 34 (12): 2259. Бибкод : 2001PatRe..34.2259C . CiteSeerX   10.1.1.119.2886 . дои : 10.1016/S0031-3203(00)00149-7 . S2CID   205904573 . В этом обзоре литературы по компьютерному зрению кратко суммируются исследования в области сегментации цветных изображений, в том числе с использованием представлений HSV и HSI.
• Фэйрчайлд, Марк Д. (2005). Модели цветового внешнего вида (2-е изд.). Аддисон-Уэсли. В этой книге не обсуждаются конкретно HSL или HSV, но она является одним из наиболее читаемых и точных ресурсов по современной науке о цвете.
• Фоли, Джей Ди ; и др. (1995). Компьютерная графика: принципы и практика (2-е изд.). Редвуд-Сити, Калифорния: Аддисон-Уэсли. ISBN  978-0-201-84840-3 . В этом стандартном учебнике компьютерной графики 1990-х годов есть глава, полная алгоритмов преобразования цветовых моделей на C. языке
• Хэнбери, Аллан; Серра, Жан (декабрь 2002 г.). Представление цвета в 3D-полярных координатах, подходящее для анализа изображений . Вена, Австрия: Венский технологический университет. {{cite book}}: |work= игнорируется ( помогите )
• Хэнбери, Аллан (2008). «Построение цветовых пространств цилиндрических координат» (PDF) . Буквы для распознавания образов . 29 (4): 494–500. Бибкод : 2008PaReL..29..494H . CiteSeerX   10.1.1.211.6425 . дои : 10.1016/j.patrec.2007.11.002 .
• Джоблав, Джордж Х.; Гринберг, Дональд (август 1978 г.). «Цветовые пространства для компьютерной графики» (PDF) . Компьютерная графика . 12 (3): 20–25. дои : 10.1145/965139.807362 . Статья Джолава и Гринберга была первой, описывающей модель HSL, которую она сравнивает с HSV.
• Куени, Рольф Г. (2003). Цветовое пространство и его подразделения: порядок цветов от древности до наших дней . Нью-Йорк: Уайли. ISBN  978-0-471-32670-0 . В этой книге лишь вкратце упоминаются HSL и HSV, но она представляет собой исчерпывающее описание систем порядка цветов на протяжении всей истории.
• Левковиц, Хаим; Герман, Габор Т. (1993). «GLHS: обобщенная цветовая модель яркости, оттенка и насыщенности». CVGIP: Графические модели и обработка изображений . 55 (4): 271–285. дои : 10.1006/cgip.1993.1019 . В этой статье объясняется, как HSL и HSV, а также другие подобные модели можно рассматривать как конкретные варианты более общей модели «GLHS». Левковиц и Герман предоставляют псевдокод для преобразования из RGB в GLHS и обратно.
• МакЭвой, Брюс (январь 2010 г.). «Цветное зрение» . Handprint.com . . Особенно разделы «Современные цветовые модели» и «Современная теория цвета» . Обширный сайт MacEvoy, посвященный науке о цвете и смешиванию красок, является одним из лучших ресурсов в Интернете. На этой странице он объясняет атрибуты создания цвета, а также общие цели и историю систем порядка цветов, включая HSL и HSV, а также их практическое значение для художников.
• Пойнтон, Чарльз (1997). «Часто задаваемые вопросы о цвете» . poynton.com . На этой самостоятельно опубликованной странице часто задаваемых вопросов эксперта по цифровому видео Чарльза Пойнтона объясняется, среди прочего, почему, по его мнению, эти модели «бесполезны для определения точного цвета» и от них следует отказаться в пользу более психометрически релевантных моделей. .
• Пойнтон, Чарльз (2008). « YUV и яркость считаются вредными» . poynton.com . Проверено 30 августа 2017 г.
• Смит, Элви Рэй (август 1978 г.). «Пары преобразования цветовой гаммы» . Компьютерная графика . 12 (3): 12–19. дои : 10.1145/965139.807361 . Это оригинальная статья, описывающая модель «гексконуса» HSV. Смит работал исследователем в Нью-Йоркского технологического института лаборатории компьютерной графики . Он описывает использование HSV в одной из первых программ цифровой живописи .

Внешние ссылки

• Демонстрационный апплет преобразования цвета
• Цвета HSV от Гектора Зенила, Демонстрационный проект Wolfram .
• HSV в RGB от CodeBeautify.