Линейчатая поверхность

Определение линейчатой ​​поверхности: каждая точка лежит на прямой.

В геометрии поверхность S в трехмерном евклидовом пространстве называется линейчатой ​​( также называемой свитком , если через каждую точку S ) проходит прямая линия лежащая на S. , Примеры включают плоскость , боковую поверхность цилиндра или конуса , коническую поверхность с эллиптической направляющей , правый коноид , геликоид и касательную, развивающуюся к гладкой кривой в пространстве.

Линейчатую поверхность можно описать как множество точек, по которым проходит движущаяся прямая. Например, конус формируется путем фиксации одной точки линии при перемещении другой точки по окружности . Поверхность называется дваждылинейчатой , если через каждую ее точку проходят две различные прямые, лежащие на поверхности. Гиперболический параболоид и однолистный гиперболоид представляют собой двулинейчатые поверхности. Плоскость — единственная поверхность, которая содержит как минимум три различные линии, проходящие через каждую из ее точек ( Фукс и Табачников, 2007 ).

Свойства управляемости или двойной управляемости сохраняются проективными отображениями и, следовательно, являются понятиями проективной геометрии . В алгебраической геометрии линейчатые поверхности иногда считаются поверхностями в аффинном или проективном пространстве над полем , но их также иногда рассматривают как абстрактные алгебраические поверхности без вложения в аффинное или проективное пространство, и в этом случае под «прямой линией» понимается означают аффинную или проективную прямую.

Определение и параметрическое представление

Линейчатая поверхность, созданная двумя кривыми Безье в качестве направляющих (красная, зеленая)

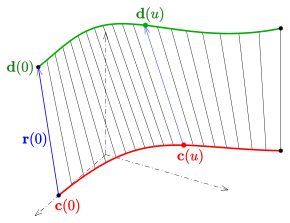
Поверхность в если трехмерном евклидовом пространстве называется линейчатой, она представляет собой объединение дифференцируемого однопараметрического семейства прямых.Формально линейчатая поверхность – это поверхность в $\mathbb {R} ^{3}$ описывается параметрическим представлением вида

$\quad \mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)$

для $u$ варьируется на интервале и $v$ начиная с реальных значений. Требуется, чтобы $\mathbf {r} (u)\neq (0,0,0)$и оба $\mathbf {c}$ и $\mathbf {r}$ должно быть дифференцируемым.

Любая прямая $v\mapsto \mathbf {x} (u_{0},v)$ с фиксированным параметром $u=u_{0}$ называется генератором . Векторы $\mathbf {r} (u)$ описать направления образующих. Кривая $u\mapsto \mathbf {c} (u)$ называется директрисой представления. Директриса может свернуться в точку (в случае конуса см. пример ниже).

Линейчатую поверхность выше можно альтернативно описать как

$\quad \mathbf {x} (u,v)=(1-v)\mathbf {c} (u)+v\mathbf {d} (u)$

со второй директрисой $\mathbf {d} (u)=\mathbf {c} (u)+\mathbf {r} (u)$. Вернемся к первому описанию, начиная с двух непересекающихся кривых. $\mathbf {c} (u),\mathbf {d} (u)$ руководящие принципы ace, набор $\mathbf {r} (u)=\mathbf {d} (u)-\mathbf {c} (u).$

Геометрическая форма директрис и образующих, конечно, важна для формы линейчатой ​​поверхности, которую они создают. Однако их конкретные параметрические представления также влияют на форму линейчатой ​​поверхности.

Примеры

Правый круглый цилиндр

Дополнительная информация: Правый круглый цилиндр.

цилиндр, конус

Прямой круговой цилиндр задается уравнением

$x^{2}+y^{2}=a^{2}.$

Его можно параметризовать как

$\mathbf {x} (u,v)=(a\cos u,a\sin u,v)$

$=(a\cos u,a\sin u,0)+v(0,0,1)$

$=(1-v)(a\cos u,a\sin u,0)+v(a\cos u,a\sin u,1).$

с

$\mathbf {c} (u)=(a\cos u,a\sin u,0),$

$\mathbf {r} (u)=(0,0,1),$

$\mathbf {d} (u)=(a\cos u,a\sin u,1).$

Правый круглый конус

Дополнительная информация: Правый круглый конус.

Прямой круговой цилиндр задается уравнением

$x^{2}+y^{2}=z^{2}.$

Его можно параметризовать как

$\mathbf {x} (u,v)=(\cos u,\sin u,1)+v(\cos u,\sin u,1)$

$=(1-v)(\cos u,\sin u,1)+v(2\cos u,2\sin u,2).$

с

$\mathbf {c} (u)=(\cos u,\sin u,1),$

$\mathbf {r} (u)=(\cos u,\sin u,1),$

$\mathbf {d} (u)=(2\cos u,2\sin u,2).$

можно было бы использовать вершину В этом случае в качестве направляющей , т.е.

$\mathbf {c} (u)=(0,0,0)$

и

$\mathbf {r} (u)=(\cos u,\sin u,1)$

как направление линии.

Для любого конуса в качестве направляющей можно выбрать вершину. Это показывает, что директриса линейчатой ​​поверхности может вырождаться в точку .

геликоид

Дополнительная информация: Геликоид.

геликоид

Геликоид можно параметризовать как

$\mathbf {x} (u,v)=(v\cos u,v\sin u,ku)$

$=(0,0,ku)+v(\cos u,\sin u,0)$

$=(1-v)(0,0,ku)+v(\cos u,\sin u,ku).$

Директриса

$\mathbf {c} (u)=(0,0,ku)$

— ось z, направления линий

$\mathbf {r} (u)=(\cos u,\sin u,0)$,

и вторая директриса

$\mathbf {d} (u)=(\cos u,\sin u,ku)$

представляет собой спираль .

Геликоид — частный случай линейчатых обобщенных геликоидов .

Цилиндр, конус и гиперболоиды

Дополнительная информация: Гиперболоид.

однолистный гиперболоид для $\varphi =63^{\circ }$

Параметрическое представление

$\mathbf {x} (u,v)=(1-v)(\cos(u-\varphi ),\sin(u-\varphi ),-1)+v(\cos(u+\varphi ),\sin(u+\varphi ),1)$

имеет два горизонтальных круга в качестве направляющих. Дополнительный параметр $\varphi$ позволяет варьировать параметрические представления окружностей. Для

$\varphi =0$ один получает цилиндр $x^{2}+y^{2}=1$,

$\varphi =\pi /2$ один получает конус $x^{2}+y^{2}=z^{2}$,

$0<\varphi <\pi /2$ получается однолистный гиперболоид с уравнением ${\frac {x^{2}+y^{2}}{a^{2}}}-{\frac {z^{2}}{c^{2}}}=1$ и полуоси $a=\cos \varphi ,c=\cot \varphi$.

Однолистный гиперболоид представляет собой двулинейчатую поверхность.

Гиперболический параболоид

Дополнительная информация: Гиперболический параболоид.

Гиперболический параболоид

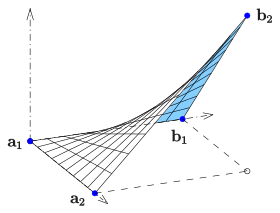
Если две директрисы в (CD) являются линиями

$\mathbf {c} (u)=(1-u)\mathbf {a} _{1}+u\mathbf {a} _{2},\quad \mathbf {d} (u)=(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}$

каждый получает

$\mathbf {x} (u,v)=(1-v){\big (}(1-u)\mathbf {a} _{1}+u\mathbf {a} _{2}{\big )}+v{\big (}(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}{\big )}$,

который представляет собой гиперболический параболоид, который интерполирует 4 точки $\mathbf {a} _{1},\mathbf {a} _{2},\mathbf {b} _{1},\mathbf {b} _{2}$ билинейно.

Поверхность двулинейчатая, поскольку любая точка лежит на двух линиях поверхности.

Для примера, показанного на схеме:

$\mathbf {a} _{1}=(0,0,0),\;\mathbf {a} _{2}=(1,0,0),\;\mathbf {b} _{1}=(0,1,0),\;\mathbf {b} _{2}=(1,1,1).$

Гиперболический параболоид имеет уравнение $z=xy$.

Лента Мёбиуса

Дополнительная информация: Лента Мёбиуса.

Лента Мёбиуса

Линейчатая поверхность

$\mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)$

с

$\mathbf {c} (u)=(\cos 2u,\sin 2u,0)$ (круг как директриса),

$\mathbf {r} (u)=(\cos u\cos 2u,\cos u\sin 2u,\sin u)\quad 0\leq u<\pi ,$

содержит ленту Мёбиуса.

На схеме изображена лента Мёбиуса для $-0.3\leq v\leq 0.3$.

Простой расчет показывает $\det(\mathbf {\dot {c}} (0),\mathbf {\dot {r}} (0),\mathbf {r} (0))\neq 0$ (см. следующий раздел). Следовательно, данная реализация ленты Мёбиуса неразвертываема . Но существуют развертывающиеся ленты Мёбиуса.

Дальнейшие примеры

• Коноид
• Каталонская поверхность
• Развертывающиеся валики ( олоид , сферикон )
• Касательная развертывающаяся

Развертывающиеся поверхности

Дополнительная информация: Развертывающаяся поверхность.

Для определения вектора нормали в точке нужны частные производные представления $\mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)$:

$\mathbf {x} _{u}=\mathbf {\dot {c}} (u)+v\mathbf {\dot {r}} (u)$,

$\mathbf {x} _{v}=\mathbf {r} (u)$.

Следовательно, нормальный вектор

$\mathbf {n} =\mathbf {x} _{u}\times \mathbf {x} _{v}=\mathbf {\dot {c}} \times \mathbf {r} +v(\mathbf {\dot {r}} \times \mathbf {r} ).$

С $\mathbf {n} \cdot \mathbf {r} =0$ (Смешанное произведение с двумя равными векторами всегда равно 0), $\mathbf {r} (u_{0})$ является касательным вектором в любой точке $\mathbf {x} (u_{0},v)$. Касательные плоскости вдоль этой прямой все одинаковы, если $\mathbf {\dot {r}} \times \mathbf {r}$ кратно $\mathbf {\dot {c}} \times \mathbf {r}$. Это возможно только в том случае, если три вектора $\mathbf {\dot {c}} ,\mathbf {\dot {r}} ,\mathbf {r}$ лежат в плоскости, т. е. если они линейно зависимы. Линейную зависимость трех векторов можно проверить с помощью определителя этих векторов:

Касательные плоскости вдоль прямой $\mathbf {x} (u_{0},v)=\mathbf {c} (u_{0})+v\mathbf {r} (u_{0})$ равны, если

$\det(\mathbf {\dot {c}} (u_{0}),\mathbf {\dot {r}} (u_{0}),\mathbf {r} (u_{0}))=0$.

Гладкая поверхность с нулевой гауссовой кривизной называется развертывающейся в плоскость или просто развертывающейся . Определяющее условие можно использовать для доказательства следующего утверждения:

Линейчатая поверхность $\mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)$ развертывается тогда и только тогда, когда

$\det(\mathbf {\dot {c}} ,\mathbf {\dot {r}} ,\mathbf {r} )=0$

в каждой точке.

Образующие любой линейчатой ​​поверхности объединяются с одним семейством ее асимптотических линий. Для развертывающихся поверхностей они также образуют одно семейство линий кривизны . Можно показать, что любая развертывающаяся поверхность представляет собой конус, цилиндр или поверхность, образованную всеми касательными пространственной кривой.

Развертывающееся соединение двух эллипсов и его развитие.

Определяющее условие развертываемости поверхностей используется для определения численно развертывающихся связей между пространственными кривыми (направлениями). На схеме изображена развертывающаяся связь между двумя эллипсами, содержащимися в разных плоскостях (один горизонтальный, другой вертикальный), и ее развитие.

Впечатление об использовании развертывающихся поверхностей в системе автоматизированного проектирования ( САПР ) дано в разделе «Интерактивное проектирование развертывающихся поверхностей» .

Исторический » обзор развертывающихся поверхностей можно найти в книге « Развертывающиеся поверхности: их история и применение .

Линейчатые поверхности в алгебраической геометрии

Основная статья: Правильный сорт

В алгебраической геометрии линейчатые поверхности первоначально определялись как проективные поверхности в проективном пространстве, содержащие прямую линию, проходящую через любую заданную точку. Это немедленно подразумевает, что на поверхности существует проективная линия, проходящая через любую данную точку, и это условие теперь часто используется в качестве определения линейчатой ​​поверхности: линейчатые поверхности определяются как абстрактные проективные поверхности, удовлетворяющие условию существования проективной линии. через любую точку. Это эквивалентно утверждению, что они бирациональны произведению кривой и проективной прямой. Иногда линейчатая поверхность определяется как поверхность, удовлетворяющая более сильному условию, заключающемуся в том, что она имеет расслоение над кривой со слоями, которые являются проективными прямыми. Это исключает проективную плоскость, которая имеет проективную линию через каждую точку, но не может быть записана как такое расслоение.

Линейчатые поверхности появляются в Энриквеса классификации проективных комплексных поверхностей , поскольку каждая алгебраическая поверхность размерности Кодайры $-\infty$ является линейчатой ​​поверхностью (или проективной плоскостью, если использовать ограничительное определение линейчатой ​​поверхности). Каждая минимальная проективная линейчатая поверхность, отличная от проективной плоскости, является проективным расслоением двумерного векторного расслоения над некоторой кривой. Линейчатые поверхности с базовой кривой рода 0 являются поверхностями Хирцебруха .

Линейчатые поверхности в архитектуре

Поверхности с двойной линейкой послужили источником вдохновения для создания изогнутых гиперболоидных структур , которые можно построить с помощью решетки из прямых элементов, а именно:

• Гиперболические параболоиды, такие как односкатные крыши .
• Однолистные гиперболоиды, такие как градирни и некоторые мусорные баки .

RM -81 Agena В ракетном двигателе использовались прямые каналы охлаждения , расположенные на линейчатой ​​поверхности и образующие горло сопловой части .

• 
  Охлаждающие гиперболические башни на электростанции Дидкот , Великобритания; поверхность может быть дважды линейчатой.
• 
  Двойная водонапорная башня с тороидальным резервуаром работы Яна Богуславского в Цеханове , Польша.
• 
  Гиперболоид Кобе Порт Тауэр , Кобе , Япония, с двойной линейкой.
• 
  Гиперболоидная водонапорная башня, 1896 год, Нижний Новгород .
• 
  Решетчатая оболочка Шуховской башни в Москве, секции которой имеют двойную линейку.
• 
  Винтовая винтовая лестница с линейками внутри Кремоне в Торраццо .
• 
  Деревенская церковь в Село, Словения: и крыша (коническая), и стена (цилиндрическая) представляют собой линованные поверхности.
• 
  Гиперболическая параболоидная крыша железнодорожной станции Варшава Охота в Варшаве , Польша.
• 
  Линейчатая коническая шляпа .
• 
  Гофрированная черепица имеет параллельные линии в одном направлении и синусоидальные в перпендикулярном направлении.
• 
  Устройство плоской поверхности путем выравнивания ( стяжки ) бетона

Ссылки

Источники

• ду Карму, Манфредо П. (1976), Дифференциальная геометрия кривых и поверхностей (1-е изд.), Прентис-Холл, ISBN  978-0132125895
• Барт, Вольф П.; Хулек, Клаус; Питерс, Крис AM; Ван де Вен, Антониус (2004), Компактные комплексные поверхности , результаты математики и ее пограничные области. 3-я серия, том. 4, Шпрингер-Верлаг, Берлин, номер номера : 10.1007/978-3-642-57739-0 , ISBN.  978-3-540-00832-3 , МР   2030225
• Бовилль, Арно (1996), Комплексные алгебраические поверхности , Студенческие тексты Лондонского математического общества, том. 34 (2-е изд.), Cambridge University Press , номер документа : 10.1017/CBO9780511623936 , ISBN.  978-0-521-49510-3 , МР   1406314
• Эдж, WL (1931), Теория линейчатых поверхностей , Издательство Кембриджского университета – через Интернет-архив . Обзор: Бюллетень Американского математического общества 37 (1931), 791–793, два : 10.1090/S0002-9904-1931-05248-4
• Фукс, Д.; Табачников, Серж (2007), «16.5 Не существует неплоских трехлинейчатых поверхностей», Математический омнибус: тридцать лекций по классической математике , Американское математическое общество, стр. 228, ISBN  9780821843161 .
• Ли, Та-цзянь, изд. (2011), Проблемы и решения по математике, 3103 (2-е изд.), World Scientific Publishing Company , ISBN  9789810234805 .
• Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN  978-0-8284-1087-8 .
• Исковских, В.А. (2001) [1994], «Линейчатая поверхность» , Энциклопедия Математики , EMS Press
• Шарп, Джон (2008), D-формы: удивительные новые трехмерные формы из плоских изогнутых форм , Тарквин, ISBN  978-1-899618-87-3 . Обзор: Секин, Карло Х. (2009), Журнал математики и искусств 3: 229–230, дои : 10.1080/17513470903332913

Внешние ссылки

• Вайсштейн, Эрик В. «Управляемая поверхность» . Математический мир .
• Фотографии линейчатой ​​поверхности из Университета Аризоны.
• Примеры развертывающихся поверхностей на сайте Rhino3DE