Музыкальная акустика

Музыкальная акустика или музыкальная акустика — междисциплинарная область, сочетающая в себе знания физики , ^{[ 1 ]}^{[ 2 ]}^{[ 3 ]} психофизика , ^{[ 4 ]} органология ^{[ 5 ]} (классификация инструментов), физиология , ^{[ 6 ]} теория музыки , ^{[ 7 ]} этномузыкология , ^{[ 8 ]} обработка сигналов и приборостроение, ^{[ 9 ]} среди других дисциплин. Как раздел акустики , он занимается исследованием и описанием физики музыки – того, как звуки используются для создания музыки. Примерами областей исследования являются функции музыкальных инструментов , человеческого голоса (физика речи и пения ), компьютерный анализ мелодии и клиническое использование музыки в музыкотерапии .

Пионером музыкальной акустики был Герман фон Гельмгольц , немецкий эрудит XIX века, влиятельный врач , физик , физиолог, музыкант, математик и философ. Его книга «Об ощущениях звука как физиологическая основа теории музыки». ^{[ 7 ]} представляет собой революционный сборник нескольких исследований и подходов, который открыл совершенно новый взгляд на теорию музыки , музыкальное исполнение, музыкальную психологию и физическое поведение музыкальных инструментов.

Методы и области исследования

Физика музыкальных инструментов
Частотный диапазон музыки
Фурье-анализ
Компьютерный анализ музыкальной структуры
Синтез музыкальных звуков
Музыкальное познание , основанное на физике (также известное как психоакустика )

Физические аспекты

Звуковая спектрография инфразвуковой записи 30301

Спектрограмма скрипки, играющей ноту, а затем идеальную квинту над ней. Общие фрагменты выделены белыми черточками.

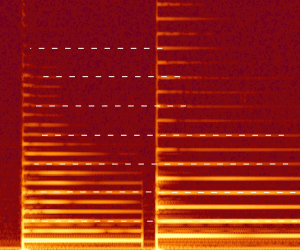
Всякий раз, когда одновременно воспроизводятся два разных тона, их звуковые волны взаимодействуют друг с другом — высокие и низкие значения давления воздуха усиливают друг друга, создавая разные звуковые волны. Любую повторяющуюся звуковую волну, не являющуюся синусоидальной, можно смоделировать множеством различных синусоидальных волн соответствующих частот и амплитуд ( частотный спектр ). У людей слуховой аппарат (состоящий из ушей и мозга ) обычно способен изолировать эти звуки и отчетливо слышать их. Когда одновременно воспроизводятся два или более тонов, изменение давления воздуха в ухе «содержит» высоту каждого тона, а ухо и/или мозг изолируют и декодируют их в отдельные тона.

Когда исходные источники звука являются совершенно периодическими, нота состоит из нескольких связанных синусоидальных волн (которые математически суммируются друг с другом), называемых основной и гармониками , частичными или обертонами . Звуки имеют гармонический частотный спектр . Самая низкая присутствующая частота является основной и является частотой, на которой колеблется вся волна. Обертоны вибрируют быстрее, чем основной тон, но должны вибрировать с целочисленной частотой, кратной основной частоте, чтобы общая волна была точно такой же в каждом цикле. Реальные инструменты близки к периодическим, но частоты обертонов немного неидеальны, поэтому форма волны незначительно меняется со временем. ^{[ нужна ссылка ]}

Субъективные аспекты

Изменения воздуха давления на барабанную перепонку и последующая физическая и неврологическая обработка и интерпретация приводят к возникновению субъективного опыта, называемого звуком . В большинстве звуков, которые люди признают музыкальными, преобладают периодические или регулярные вибрации, а не непериодические; то есть музыкальные звуки обычно имеют определенную высоту . Передача этих изменений через воздух осуществляется посредством звуковой волны . В очень простом случае звук синусоидальной волны , который считается самой базовой моделью звуковой волны, вызывает регулярное увеличение и уменьшение давления воздуха и воспринимается как очень чистый тон. Чистые тона можно получить с помощью камертонов или свиста . Скорость, с которой колеблется давление воздуха, — это частота тона, измеряемая в колебаниях в секунду и называемая герцами . Частота является основным фактором, определяющим воспринимаемую высоту звука . Частота музыкальных инструментов может меняться с высотой из-за изменения давления воздуха.

Диапазоны звуков музыкальных инструментов

* Эта таблица отображается только до C ₀ , хотя некоторые органы, такие как орган Boardwalk Hall Auditorium , простираются до C ₋₁ (на одну октаву ниже C ₀ ). Кроме того, основная частота субконтрабасовой тубы равна B ♭ ₋₁ .

Гармоники, частичные и обертоны

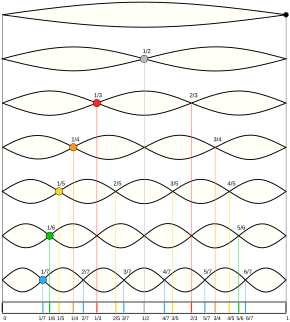
Фундаментальным . является частота, на которой колеблется вся волна Обертоны — это другие синусоидальные компоненты, присутствующие на частотах выше основного. Все частотные компоненты, составляющие общую форму сигнала, включая основной тон и обертоны, называются частичными . Вместе они образуют гармонический ряд .

Обертоны, которые являются целыми кратными основному тону, называются гармониками . Когда обертон близок к гармоническому, но не точный, его иногда называют гармоническим частичным, хотя их часто называют просто гармониками. Иногда создаются обертоны, далекие от гармонических, и их называют просто частичными или негармоничными обертонами.

Основная частота считается первой гармоникой и первой частичной. Нумерация частичных и гармоник в этом случае обычно одинакова; второй парциал — вторая гармоника и т. д. Но если есть негармонические парциалы, то нумерация уже не совпадает. Обертоны нумеруются по мере их появления над основным. Строго говоря, первый обертон — это вторая частичная (и обычно вторая гармоника). Поскольку это может привести к путанице, обычно только гармоники обозначаются по их номерам, а обертоны и частичные описываются по их отношению к этим гармоникам.

Гармоники и нелинейности

Когда периодическая волна состоит из основной и только нечетных гармоник ( $f$ , $3 f$ , $5 f$ , $7 f$ ,...), суммированная волна является полуволновой симметричной ; его можно инвертировать и сдвинуть по фазе, и он будет точно таким же. Если в волне есть четные гармоники ( $2 f$ , $4 f$ , $6 f$ , ...), она асимметрична ; верхняя половина построенной формы волны не является зеркальным отражением нижней.

И наоборот, система, которая меняет форму волны (помимо простого масштабирования или смещения), создает дополнительные гармоники ( гармонические искажения ). Это называется нелинейной системой . Если он воздействует на волну симметрично, все возникающие гармоники будут нечетными. Если он влияет на гармоники асимметрично, возникает хотя бы одна четная гармоника (и, возможно, также нечетные гармоники).

Гармония

Если одновременно звучат две ноты, соотношение частот которых представляет собой простые дроби (например, ⁠  2  /  1  ⁠ , ⁠ 3 / 2 ⁠ , или ⁠ 5 / 4 ⁠ ), составная волна по-прежнему периодическая, с коротким периодом – и сочетание звучит созвучно . Например, нота, вибрирующая с частотой 200 Гц , и нота, вибрирующая с частотой 300 Гц ( идеальная квинта , или ⁠ 3/2 выше 200 Гц) складываются вместе , чтобы получить ⁠ соотношение, волну, повторяющуюся с частотой 100 Гц: Каждые ⁠ 1/100 . дважды ⁠ секунды волна 300 Гц повторяется три раза, а волна 200 Гц повторяется Обратите внимание, что объединенная волна повторяется с частотой 100 Гц, хотя фактической синусоидальной составляющей 100 Гц, вносимой отдельным источником звука, не существует.

Кроме того, две ноты акустических инструментов будут иметь частичные обертоны, которые будут включать в себя множество нот, имеющих одну и ту же частоту. Например, нота с частотой основной гармоники 200 Гц может иметь гармонические обертоны на частотах: 400, 600, 800, 1 000 , 1 200 , 1 400 , 1 600 , 1 800 , ... Гц . Нота с основной частотой 300 Гц может иметь обертоны на частотах: 600, 900, 1 200 , 1 500 , 1 800 , ... Гц . Эти две ноты имеют общие гармоники на частотах 600, 1 200 , 1 800 Гц и более, которые совпадают друг с другом в каждой серии.

Хотя механизм человеческого слуха, обеспечивающий это, до сих пор не до конца понятен, практические музыкальные наблюдения на протяжении 2000 почти лет ^{[ 10 ]} Комбинация составных волн с короткими основными частотами и общими или тесно связанными частичными частотами — вот что вызывает ощущение гармонии: когда две частоты близки к простой дроби, но не точны, составная волна колеблется достаточно медленно, чтобы услышать подавление волн. как устойчивая пульсация вместо тона. Это называется избиением и считается неприятным или диссонирующим .

Частота биения рассчитывается как разница между частотами двух нот. Когда две ноты близки по высоте, они бьются достаточно медленно, чтобы человек мог измерить разницу частот на слух с помощью секундомера ; такт ритма — это то, как настраивали фортепиано, арфы и клавесины на сложные темпераменты до появления доступных измерителей настройки .

В приведенном выше примере $| 200$ Гц $- 300$ Гц $| = 100$ Гц.

Еще один пример из теории модуляции : комбинация частот 3 425 Гц и 3 426 Гц будет биться один раз в секунду, поскольку $| 3425$ Гц $- 3426$ Гц $| = 1$ Гц.

Разница между консонансом и диссонансом четко не определена, но чем выше частота биений, тем вероятнее, что интервал диссонансный. Гельмгольц предположил, что максимальный диссонанс возникает между двумя чистыми тонами, когда частота биений составляет примерно 35 Гц. ^{[ 11 ]}

Весы

Материал музыкальной композиции обычно берется из набора высот, известного как гамма . Поскольку большинство людей не могут адекватно определить абсолютные частоты, идентичность гаммы заключается в соотношениях частот между ее тонами (известных как интервалы ).

Диатоническая гамма появляется в письменном виде на протяжении всей истории, состоящая из семи тонов в каждой октаве . С помощью простой интонации диатоническую гамму можно легко построить, используя три простейших интервала внутри октавы: идеальную квинту (3/2), идеальную кварту (4/3) и мажорную треть (5/4). гармонических резонаторов естественно присутствуют формы пятой и третьей Поскольку в обертонном ряду , то это очень простой процесс.

В следующей таблице показано соотношение частот всех нот только мажорной гаммы и фиксированной частоты первой ноты гаммы.

С	Д	И	Ф	Г	А	Б	С
1	9/8	5/4	4/3	3/2	5/3	15/8	2

Есть и другие гаммы, доступные только через интонацию, например минорная гамма . Весы, которые не придерживаются только интонации, а вместо этого их интервалы корректируются для удовлетворения других потребностей, называются темпераментами , из которых равная темперация наиболее часто используется . Темпераменты, хотя и скрывают акустическую чистоту интервалов, часто обладают желательными свойствами, такими как замкнутый круг квинт .

См. также

Акустический резонанс
Киматика
Математика музыкальных гамм
Струнный резонанс
Вибрирующая струна
3-й мост (гармонический резонанс, основанный на равных делениях струн)
Базовая физика скрипки

Ссылки

^ Бенаде, Артур Х. (1990). Основы музыкальной акустики . Дуврские публикации. ISBN 9780486264844 .
^ Флетчер, Невилл Х.; Россинг, Томас (23 мая 2008 г.). Физика музыкальных инструментов . Springer Science & Business Media. ISBN 9780387983745 .
^ Кэмпбелл, Мюррей; Грейтед, Клайв (28 апреля 1994 г.). Руководство музыканта по акустике . ОУП Оксфорд. ISBN 9780191591679 .
^ Редерер, Хуан (2009). Физика и психофизика музыки: Введение (4-е изд.). Нью-Йорк: Springer Verlag. ISBN 9780387094700 .
^ Генри, Луи Л. (2002). Музыкальная акустика (на португальском языке). Фонд Галуста Гюльбенкяна. ISBN 9789723109870 .
^ Уотсон, Лэнхэм, Алан HD, ML (2009). Биология музыкального исполнения и травмы, связанные с исполнением . Кембридж: Scarecrow Press. ISBN 9780810863590 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Гельмгольц, Герман Л.Ф.; Эллис, Александр Дж. (1885). Об ощущениях тона как физиологической основе теории музыки Германа Л. Ф. Гельмгольца . дои : 10.1017/CBO9780511701801 . hdl : 2027/mdp.39015000592603 . ISBN 9781108001779 . Проверено 4 ноября 2019 г. {{cite book}}: |website= игнорируется ( помогите )
^ Картоми, Маргарет (1990). О понятиях и классификациях музыкальных инструментов . Чикаго: Издательство Чикагского университета. ISBN 9780226425498 .
^ Хопкин, Барт (1996). Дизайн музыкальных инструментов: практическая информация по проектированию инструментов . См. Sharp Press. ISBN 978-1884365089 .
^ Птолемей, Гай Клавдий . Гармоникон $Гармоникон$ [ Гармоники ]. год с. 180 год нашей эры .
^ «Грубость» . music-cog.ohio-state.edu (примечания к курсу). Музыка 829Б. Университет штата Огайо .

Внешние ссылки

[1] Бенаде, Артур Х. (1990). Основы музыкальной акустики . Дуврские публикации. ISBN 9780486264844 .

[2] Флетчер, Невилл Х.; Россинг, Томас (23 мая 2008 г.). Физика музыкальных инструментов . Springer Science & Business Media. ISBN 9780387983745 .

[3] Кэмпбелл, Мюррей; Грейтед, Клайв (28 апреля 1994 г.). Руководство музыканта по акустике . ОУП Оксфорд. ISBN 9780191591679 .

[4] Редерер, Хуан (2009). Физика и психофизика музыки: Введение (4-е изд.). Нью-Йорк: Springer Verlag. ISBN 9780387094700 .

[5] Генри, Луи Л. (2002). Музыкальная акустика (на португальском языке). Фонд Галуста Гюльбенкяна. ISBN 9789723109870 .

[6] Уотсон, Лэнхэм, Алан HD, ML (2009). Биология музыкального исполнения и травмы, связанные с исполнением . Кембридж: Scarecrow Press. ISBN 9780810863590 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[:0-7] Перейти обратно: ^а ^б Гельмгольц, Герман Л.Ф.; Эллис, Александр Дж. (1885). Об ощущениях тона как физиологической основе теории музыки Германа Л. Ф. Гельмгольца . дои : 10.1017/CBO9780511701801 . hdl : 2027/mdp.39015000592603 . ISBN 9781108001779 . Проверено 4 ноября 2019 г. {{cite book}}: |website= игнорируется ( помогите )

[8] Картоми, Маргарет (1990). О понятиях и классификациях музыкальных инструментов . Чикаго: Издательство Чикагского университета. ISBN 9780226425498 .

[9] Хопкин, Барт (1996). Дизайн музыкальных инструментов: практическая информация по проектированию инструментов . См. Sharp Press. ISBN 978-1884365089 .

[10] Птолемей, Гай Клавдий . Гармоникон $Гармоникон$ [ Гармоники ]. год с. 180 год нашей эры .

[11] «Грубость» . music-cog.ohio-state.edu (примечания к курсу). Музыка 829Б. Университет штата Огайо .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

v т и Акустика
Акустическая инженерия	Архитектурная акустика монохорд Реверберация Звукоизоляция Вибрация струн Симпатический резонанс	Спектрограмма
Психоакустика	Подача Чешуя коры Мел масштаб Контур равной громкости Кривые Флетчера – Мансона
Звуковая частота и высота звука	Бить Форманта Основная частота Частотный спектр гармонический спектр Гармонический Ряд Негармоничность Отсутствует фундаментальный Комбинированный тон Законы Мерсенна Обертон Резонанс Стоячая волна Узел Субгармоника
Акустики	Джон Бэкус Йенс Блауэрт Эрнст Хладни Герман фон Гельмгольц Карлин Хатчинс Франц Мельде Марин Мерсенн Вернер Мейер-Эпплер Лорд Рэлей Жозеф Совер Д. Ван Холлидей Томас Янг
Связанные темы	Эхо Инфразвук Звук УЗИ Музыкальная акустика Фортепиано Скрипка
Категория