Коэффициенты Эйнштейна

Линии излучения и линии поглощения по сравнению с непрерывным спектром

В атомной, молекулярной и оптической физике коэффициенты Эйнштейна — это величины, описывающие вероятность поглощения или испускания фотона атомом или молекулой. Коэффициенты Эйнштейна A связаны со скоростью спонтанного излучения света, а коэффициенты Эйнштейна B связаны с поглощением и вынужденным излучением света. В этой статье под словом «свет» понимается любое электромагнитное излучение , не обязательно в видимом спектре .

Эти коэффициенты названы в честь Альберта Эйнштейна , предложившего их в 1916 году.

Спектральные линии

В физике о спектральной линии думают с двух точек зрения.

Линия излучения образуется, когда атом или молекула совершает переход с определенного дискретного энергетического уровня E ₂ атома на более низкий энергетический уровень E ₁ , испуская фотон определенной энергии и длины волны. Спектр многих таких фотонов покажет всплеск излучения на длине волны, связанной с этими фотонами.

Линия поглощения образуется, когда атом или молекула совершает переход из более низкого дискретного энергетического состояния E ₁ в более высокое дискретное энергетическое состояние E ₂ , при этом фотон поглощается. Эти поглощенные фотоны обычно происходят от фонового непрерывного излучения (полного спектра электромагнитного излучения), и спектр показывает падение непрерывного излучения на длине волны, связанной с поглощенными фотонами.

Эти два состояния должны быть связанными состояниями, в которых электрон связан с атомом или молекулой, поэтому переход иногда называют переходом «связанный-связанный», в отличие от перехода, при котором электрон выбрасывается из атома. полностью («связанно-свободный» переход) в состояние континуума , оставляя ионизированный атом и генерируя континуальное излучение.

фотон с энергией , равной разнице E ₂ − E ₁ При этом выделяется или поглощается между уровнями энергии. Частота ν, на которой возникает спектральная линия, связана с энергией фотона частотным условием Бора E ₂ − E ₁ = hν , где h обозначает постоянную Планка .

Коэффициенты излучения и поглощения

Атомная спектральная линия относится к событиям излучения и поглощения в газе, в котором $n_{2}$ – плотность атомов в верхнем энергетическом состоянии линии, $n_{1}$ – плотность атомов в состоянии с более низкой энергией линии.

Излучение атомных линий на частоте ν можно описать коэффициентом излучения $\varepsilon$ с единицами энергии/(время × объём × телесный угол). ε dt dV d Ω – это энергия, излучаемая элементом объема $dV$ вовремя $dt$ в телесный угол $d\Omega$. Для излучения атомных линий $$\varepsilon ={\frac {h\nu }{4\pi }}n_{2}A_{21},$$где $A_{21}$ - коэффициент Эйнштейна для спонтанного излучения, который фиксируется внутренними свойствами соответствующего атома для двух соответствующих энергетических уровней.

Поглощение излучения атомных линий можно описать коэффициентом поглощения $\kappa$ с единицами измерения 1/длина. Выражение κ' dx дает долю интенсивности, поглощаемую световым лучом на частоте ν при прохождении расстояния dx . Коэффициент поглощения определяется выражением $$\kappa '={\frac {h\nu }{4\pi }}(n_{1}B_{12}-n_{2}B_{21}),$$где $B_{12}$ и $B_{21}$ — коэффициенты Эйнштейна для поглощения фотонов и вынужденного излучения соответственно. Как и коэффициент $A_{21}$, они также фиксируются внутренними свойствами соответствующего атома для двух соответствующих энергетических уровней. Для термодинамики и для применения закона Кирхгофа необходимо, чтобы полное поглощение выражалось как алгебраическая сумма двух компонент, описываемых соответственно формулой $B_{12}$ и $B_{21}$, которое можно рассматривать как положительное и отрицательное поглощение, которые представляют собой соответственно прямое поглощение фотонов и то, что обычно называют вынужденным или индуцированным излучением.

Приведенные выше уравнения не учитывают влияние формы спектроскопической линии . Чтобы быть точным, приведенные выше уравнения необходимо умножить на (нормализованную) форму спектральной линии, и в этом случае единицы измерения изменятся и будут включать член 1/Гц.

В условиях термодинамического равновесия плотности $n_{2}$ и $n_{1}$, коэффициенты Эйнштейна и спектральная плотность энергии предоставляют достаточную информацию для определения скоростей поглощения и излучения.

Условия равновесия

Плотность чисел $n_{2}$ и $n_{1}$ задаются физическим состоянием газа, в котором возникает спектральная линия, включая локальную спектральную яркость (или, в некоторых представлениях, локальную спектральную плотность энергии излучения ). Когда это состояние является либо состоянием строгого термодинамического равновесия , либо состоянием так называемого «локального термодинамического равновесия», то распределение атомных состояний возбуждения (в том числе $n_{2}$ и $n_{1}$) определяет скорость атомной эмиссии и поглощения так, чтобы соблюдался закон Кирхгофа о равенстве поглощательной и излучательной способности . В строгом термодинамическом равновесии поле излучения называется излучением черного тела и описывается законом Планка . Для локального термодинамического равновесия поле излучения не обязательно должно быть полем черного тела, но скорость межатомных столкновений должна значительно превышать скорости поглощения и испускания квантов света, так что межатомные столкновения полностью доминируют в распределении состояний. атомного возбуждения. Возникают обстоятельства, при которых локальное термодинамическое равновесие не преобладает, поскольку сильные радиационные эффекты подавляют тенденцию к Максвелла-Больцмана распределению молекулярных скоростей . Например, в атмосфере Солнца господствует большая сила излучения. В верхних слоях атмосферы Земли, на высотах более 100 км, решающее значение имеет редкость межмолекулярных столкновений.

В случаях термодинамического равновесия и локального термодинамического равновесия плотность атомов, как возбужденных, так и невозбужденных, может быть рассчитана из распределения Максвелла-Больцмана , но для других случаев (например, лазеров ) расчет более сложен.

Коэффициенты Эйнштейна

В 1916 году Альберт Эйнштейн предположил, что при формировании атомной спектральной линии происходят три процесса. Эти три процесса называются спонтанным излучением, вынужденным излучением и поглощением. С каждым связан коэффициент Эйнштейна, который является мерой вероятности возникновения этого конкретного процесса. Эйнштейн рассматривал случай изотропного излучения с частотой ν и спектральной плотностью энергии ρ ( ν ) . Поль Дирак вывел коэффициенты в статье 1927 года под названием «Квантовая теория испускания и поглощения излучения».

Различные составы

Хилборн сравнил различные формулировки вывода коэффициентов Эйнштейна, предложенные разными авторами. Например, Герцберг работает с излучением и волновым числом; Ярив работает с энергией единицы объема на единицу частотного интервала, как и в более позднем (2008 г.) формулировка. Михалас и Вайбель-Михалас работают с сиянием и частотой; также Чандрасекар; также Гуди и Юнг; Лаудон использует угловую частоту и излучение.

Спонтанное излучение

Основная статья: Спонтанное излучение

Принципиальная схема атомного спонтанного излучения

Спонтанная эмиссия — это процесс, при котором электрон «самопроизвольно» (т.е. без какого-либо внешнего воздействия) распадается с более высокого энергетического уровня на более низкий. Процесс описывается коэффициентом Эйнштейна A ₂₁ ( s ⁻¹ ), что дает вероятность в единицу времени того, что электрон в состоянии 2 с энергией $E_{2}$ самопроизвольно распадется в состояние 1 с энергией $E_{1}$, испуская фотон с энергией E ₂ − E ₁ = hν . Из-за принципа неопределенности энергии и времени переход фактически производит фотоны в узком диапазоне частот, называемом шириной спектральной линии . Если $n_{i}$ — плотность атомов в состоянии i , то изменение плотности атомов в состоянии 2 в единицу времени за счёт спонтанного излучения будет $$\left({\frac {dn_{2}}{dt}}\right)_{\text{spontaneous}}=-A_{21}n_{2}.$$

Тот же процесс приводит к увеличению населения штата 1: $$\left({\frac {dn_{1}}{dt}}\right)_{\text{spontaneous}}=A_{21}n_{2}.$$

Вынужденное излучение

Основная статья: Вынужденное излучение

Принципиальная схема атомно-стимулированной эмиссии

Вынужденная эмиссия (также известная как индуцированная эмиссия) — это процесс, при котором электрон вынужден перепрыгнуть с более высокого энергетического уровня на более низкий из-за присутствия электромагнитного излучения на частоте перехода (или близкой к ней). С термодинамической точки зрения этот процесс следует рассматривать как отрицательное поглощение. Процесс описывается коэффициентом Эйнштейна $B_{21}$ (м ³ Дж ⁻¹ с ⁻² ), что дает вероятность в единицу времени на единицу плотности энергии поля излучения на единицу частоты того, что электрон в состоянии 2 с энергией $E_{2}$ распадется в состояние 1 с энергией $E_{1}$, испуская фотон с энергией E ₂ − E ₁ = hν . Изменение плотности атомов в состоянии 1 в единицу времени за счет вынужденной эмиссии будет $$\left({\frac {dn_{1}}{dt}}\right)_{\text{neg. absorb.}}=B_{21}n_{2}\rho (\nu ),$$где $\rho (\nu )$ обозначает спектральную плотность энергии поля изотропного излучения на частоте перехода (см. закон Планка ).

Вынужденное излучение — один из фундаментальных процессов, приведших к созданию лазера . Однако лазерное излучение очень далеко от современного случая изотропного излучения.

Поглощение фотонов

Основная статья: Поглощение (оптика)

Принципиальная схема атомной абсорбции

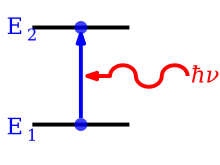
Поглощение — это процесс, при котором фотон поглощается атомом, заставляя электрон перепрыгнуть с более низкого энергетического уровня на более высокий. Процесс описывается коэффициентом Эйнштейна $B_{12}$ (м ³ Дж ⁻¹ с ⁻² ), что дает вероятность в единицу времени на единицу плотности энергии поля излучения на единицу частоты того, что электрон в состоянии 1 с энергией $E_{1}$ поглотит фотон с энергией E ₂ − E ₁ = hν и перейдет в состояние 2 с энергией $E_{2}$. Изменение плотности атомов в состоянии 1 в единицу времени за счет поглощения будет $$\left({\frac {dn_{1}}{dt}}\right)_{\text{pos. absorb.}}=-B_{12}n_{1}\rho (\nu ).$$

Детальная балансировка

Коэффициенты Эйнштейна представляют собой фиксированные вероятности в каждый момент времени, связанные с каждым атомом, и не зависят от состояния газа, частью которого являются атомы. Следовательно, любое соотношение, которое мы можем вывести между коэффициентами, скажем, при термодинамическом равновесии, будет универсальным.

При термодинамическом равновесии мы будем иметь простое балансирование, при котором чистое изменение числа любых возбужденных атомов равно нулю и уравновешивается потерями и выигрышами в результате всех процессов. Что касается связанных-связанных переходов, у нас также будет подробная балансировка , которая утверждает, что чистый обмен между любыми двумя уровнями будет сбалансирован. Это связано с тем, что на вероятности перехода не может влиять наличие или отсутствие других возбужденных атомов. Детальный баланс (действителен только в состоянии равновесия) требует, чтобы изменение во времени количества атомов на уровне 1 вследствие трех вышеуказанных процессов было равно нулю: $$0=A_{21}n_{2}+B_{21}n_{2}\rho (\nu )-B_{12}n_{1}\rho (\nu ).$$

Наряду с детальной балансировкой, при температуре T мы можем использовать наши знания о равновесном распределении энергии атомов, как указано в распределении Максвелла-Больцмана , и равновесном распределении фотонов, как указано в законе излучения черного тела Планка, чтобы получить универсальные соотношения между коэффициентами Эйнштейна.

Из распределения Больцмана мы имеем для числа возбужденных видов атомов i : $${\frac {n_{i}}{n}}={\frac {g_{i}e^{-E_{i}/kT}}{Z}},$$где n — общая плотность атомных частиц, возбужденных и невозбужденных, k — постоянная Больцмана , T — температура , $g_{i}$ — вырождение (также называемое кратностью) состояния i , а Z — статистическая сумма . Из закона Планка об излучении черного тела при температуре T мы имеем для спектральной яркости (сияние - это энергия в единицу времени на единицу телесного угла на единицу проецируемой площади при интегрировании по соответствующему спектральному интервалу) на частоте ν $$\rho _{\nu }(\nu ,T)=F(\nu ){\frac {1}{e^{h\nu /kT}-1}},$$где $$F(\nu )={\frac {2h\nu ^{3}}{c^{2}}},$$где $c$ это скорость света и $h$ — постоянная Планка .

Подставляя эти выражения в уравнение детальной балансировки и учитывая, что E ₂ − E ₁ = hν , получаем $$A_{21}g_{2}e^{-h\nu /kT}+B_{21}g_{2}e^{-h\nu /kT}{\frac {F(\nu )}{e^{h\nu /kT}-1}}=B_{12}g_{1}{\frac {F(\nu )}{e^{h\nu /kT}-1}},$$или $$A_{21}g_{2}(1-e^{-h\nu /kT})+B_{21}g_{2}F(\nu )e^{-h\nu /kT}=B_{12}g_{1}F(\nu ).$$

Приведенное выше уравнение должно выполняться при любой температуре, поэтому из $T\to \infty$ каждый получает $$B_{21}g_{2}=B_{12}g_{1},$$и из $T\to 0$$$A_{21}g_{2}=B_{21}g_{2}F(\nu ).$$

Следовательно, три коэффициента Эйнштейна связаны между собой соотношением $${\frac {A_{21}}{B_{21}}}=F(\nu )$$и $${\frac {B_{21}}{B_{12}}}={\frac {g_{1}}{g_{2}}}.$$

Если это соотношение подставить в исходное уравнение, можно также найти связь между $A_{21}$ и $B_{12}$, включающий закон Планка .

Сила осциллятора

Сила осциллятора $f_{12}$ определяется следующим соотношением к сечению $\sigma$ для поглощения: $$\sigma ={\frac {e^{2}}{4\varepsilon _{0}m_{e}c}}\,f_{12}\,\phi _{\nu }={\frac {\pi e^{2}}{2\varepsilon _{0}m_{e}c}}\,f_{12}\,\phi _{\omega },$$

где $e$ - заряд электрона, $m_{e}$ - масса электрона, а $\phi _{\nu }$ и $\phi _{\omega }$ — нормированные функции распределения по частоте и угловой частоте соответственно. Это позволяет выразить все три коэффициента Эйнштейна через силу одиночного осциллятора, связанную с конкретной атомной спектральной линией: $${\begin{aligned}B_{12}&={\frac {e^{2}}{4\varepsilon _{0}m_{e}h\nu }}f_{12},\\[1ex]B_{21}&={\frac {e^{2}}{4\varepsilon _{0}m_{e}h\nu }}{\frac {g_{1}}{g_{2}}}f_{12},\\[1ex]A_{21}&={\frac {2\pi \nu ^{2}e^{2}}{\varepsilon _{0}m_{e}c^{3}}}{\frac {g_{1}}{g_{2}}}f_{12}.\end{aligned}}$$

Дипольное приближение

Значение коэффициентов A и B можно рассчитать с помощью квантовой механики, где используются дипольные приближения в теории возмущений, зависящей от времени. Хотя расчет коэффициента B можно выполнить легко, расчет коэффициента A требует использования результатов второго квантования . Это связано с тем, что теория, разработанная с помощью дипольного приближения и теории возмущений, зависящих от времени, дает квазиклассическое описание электронного перехода, который стремится к нулю, когда возмущающие поля стремятся к нулю. Коэффициент А, управляющий спонтанным излучением, не должен стремиться к нулю, поскольку возмущающие поля стремятся к нулю. Результат для скоростей перехода различных электронных уровней в результате спонтанной эмиссии определяется как (в единицах СИ): $$w_{i\to f}^{\text{s.emi}}={\frac {\omega _{if}^{3}e^{2}}{3\pi \varepsilon _{0}\hbar c^{3}}}\left|\langle f|{\vec {r}}|i\rangle \right|^{2}=A_{if}$$

Для коэффициента B прямое применение дипольного приближения в теории возмущений, зависящих от времени, дает (в единицах СИ): $$w_{i\rightarrow f}^{\text{abs}}={\frac {u(\omega _{fi})\pi e^{2}}{3\varepsilon _{0}\hbar ^{2}}}\left|\langle f|{\vec {r}}|i\rangle \right|^{2}=B_{if}^{\text{abs}}u(\omega _{fi})$$$$w_{i\to f}^{\text{emi}}={\frac {u(\omega _{if})\pi e^{2}}{3\varepsilon _{0}\hbar ^{2}}}\left|\langle f|{\vec {r}}|i\rangle \right|^{2}=B_{if}^{emi}u(\omega _{if})$$

Обратите внимание, что формула скорости перехода зависит от оператора дипольного момента. Для приближений более высокого порядка он включает квадрупольный момент и другие подобные члены.

Здесь коэффициенты B выбраны так, чтобы соответствовать $\omega$ функция распределения энергии. Часто эти разные определения коэффициентов B выделяются верхним индексом, например, ${\textstyle B_{21}^{f}={\frac {B_{21}^{\omega }}{2\pi }}}$ где ${\textstyle B_{21}^{f}}$ член соответствует частотному распределению и ${\textstyle B_{21}^{\omega }}$ термин соответствует $\omega$ распределение. Формулы для коэффициентов B изменяются обратно пропорционально выбранному распределению энергии, так что скорость перехода одинакова независимо от соглашений.

Следовательно, коэффициенты AB рассчитываются с использованием дипольного приближения как: $${\begin{aligned}A_{ab}&={\frac {\omega _{ab}^{3}e^{2}}{3\pi \varepsilon _{0}\hbar c^{3}}}\left|\langle a|{\vec {r}}|b\rangle \right|^{2}\\[1ex]B_{ab}&={\frac {\pi e^{2}}{3\varepsilon _{0}\hbar ^{2}}}\left|\langle a|{\vec {r}}|b\rangle \right|^{2}\end{aligned}}$$где $\omega _{ab}={\frac {E_{a}-E_{b}}{\hbar }}$ и коэффициенты B соответствуют $\omega$ функция распределения энергии.

Отсюда также получаются следующие соотношения: $${\frac {B_{12}}{B_{21}}}=1$$ и $${\frac {A_{if}}{B}}={\frac {\omega _{if}^{3}\hbar }{\pi ^{2}c^{3}}}$$

Вывод закона Планка

Из теории следует, что: $${\frac {dN_{b}}{dt}}=-A_{ba}N_{b}-N_{b}u(\omega _{ba})B_{ba}+N_{a}u(\omega _{ba})B_{ab}=-N_{b}w_{b\to a}^{\text{s.emi}}-N_{b}w_{b\to a}^{\text{emi}}+N_{a}w_{a\to b}^{\text{abs}}$$где $N_{a}$ и $N_{b}$ – число занятых энергетических уровней $E_{a}$ и $E_{b}$ соответственно, где $E_{b}>E_{a}$. Обратите внимание, что из применения теории возмущений, зависящей от времени, тот факт, что только излучение, чье $\omega$ близко к значению $\omega _{ba}$ может производить соответствующее стимулированное излучение или поглощение.

Где распределение Максвелла, включающее $N_{a}$ и $N_{b}$ обеспечивает ${\frac {N_{a}}{N_{b}}}={\frac {e^{-E_{a}\beta }}{e^{-E_{b}\beta }}}=e^{\omega _{ba}\hbar \beta }$

Решение для $u$ для состояния равновесия ${\frac {dN_{b}}{dt}}=0$ используя приведенные выше уравнения и соотношения при обобщении $\omega _{ba}$ к $\omega$, мы получаем: $$u_{\omega }(\omega ,T)={\frac {\omega ^{3}\hbar }{\pi ^{2}c^{3}}}{\frac {1}{e^{\omega \hbar \beta }-1}}$$что представляет собой распределение энергии по угловым частотам из закона Планка .

См. также

• Переходный дипольный момент
• Сила осциллятора
• Распределение Брейта – Вигнера
• Электронная конфигурация
• Резонанс Фано
• Обозначение Зигбана
• Атомная спектроскопия
• Молекулярное излучение , непрерывные спектры, испускаемые молекулами.

Ссылки

Цитируемая библиография

• Чандрасекхар, С. (1950). Перенос излучения , Издательство Оксфордского университета, Оксфорд.
• Гаррисон, Дж. К., Цзяо, Р. Ю. (2008). Квантовая оптика , Издательство Оксфордского университета, Оксфорд, Великобритания, ISBN   978-019-850-886-1 .
• Гуди, Р.М., Юнг, Ю.Л. (1989). Атмосферная радиация: теоретическая основа , 2-е издание, Oxford University Press, Оксфорд, Нью-Йорк, 1989, ISBN   0-19-505134-3 .
• Гейзенберг, В. (1925). «О квантово-теоретической интерпретации кинематических и механических связей». Журнал физики . 33 (1): 879–893. Бибкод : 1925ZPhy...33..879H . дои : 10.1007/BF01328377 . S2CID   186238950 . Переведено как «Квантово-теоретическая переинтерпретация кинематических и механических отношений» на английском языке.

ван дер Варден, БЛ (1967). Источники квантовой механики . Издательство Северной Голландии . стр. 261–276.

• Герцберг, Г. (1950). Молекулярная спектроскопия и молекулярная структура , вып. 1, Двухатомные молекулы , второе издание, Ван Ностранд, Нью-Йорк.
• Лаудон, Р. (1973/2000). Квантовая теория света (первое издание 1973 г.), третье издание 2000 г., Oxford University Press, Оксфорд, Великобритания, ISBN   0-19-850177-3 .
• Михалас Д., Вайбель-Михалас Б. (1984). Основы радиационной гидродинамики , Издательство Оксфордского университета, Нью-Йорк ISBN   0-19-503437-6 .
• Ярив, А. (1967/1989). Квантовая электроника , третье издание, Джон Уайли и сыновья, Нью-Йорк, ISBN   0-471-60997-8 .
• Губени, Иван; Михалас, Дмитрий (2015). Теория звездных атмосфер: введение в астрофизический неравновесный количественный спектроскопический анализ . Издательство Принстонского университета. ISBN  9780691163291 .

Другое чтение

• Кондон, ЕС; Шортли, GH (1964). Теория атомных спектров . Издательство Кембриджского университета. ISBN  0-521-09209-4 .
• Рыбицкий, ГБ; Лайтман, AP (1985). Радиационные процессы в астрофизике . Джон Уайли и сыновья, Нью-Йорк. ISBN  0-471-82759-2 .
• Шу, FH (1991). Физика астрофизики . Том. 1: Радиация. Университетские научные книги, Милл-Вэлли, Калифорния. ISBN  0-935702-64-4 .
• Роберт К. Хилборн (2002). «Коэффициенты Эйнштейна, сечения, значения f, дипольные моменты и все такое». Являюсь. Дж. Физ . 50 : 982–986. arXiv : физика/0202029 .
• Тейлор, Массачусетс; Вилчес, Дж. М. (2009). «Учебник: Точные решения для заселенностей ионов n-уровня». Публикации Тихоокеанского астрономического общества . 121 (885): 1257–1266. arXiv : 0709.3473 . Бибкод : 2009PASP..121.1257T . дои : 10.1086/648121 . S2CID   16116964 .

Внешние ссылки

• Спектры излучения от различных источников света