Проекция (математика)

В математике проекция — это идемпотентное отображение множества ) (или другой математической структуры в подмножество (или подструктуру). В данном случае идемпотентность означает, что проецирование дважды равносильно проецированию один раз. Ограничение на подпространство проекции также называется проекцией , даже если свойство идемпотентности потеряно.Бытовым примером проекции является отбрасывание тени на плоскость (лист бумаги): проекция точки — это ее тень на лист бумаги, а проекция (тень) точки на лист бумаги — это то, что сама точка (идемпотентность). Тень трехмерной сферы представляет собой закрытый диск. Первоначально понятие проекции было введено в евклидовой геометрии для обозначения проекции трехмерного евклидова пространства на плоскость в нем, как в примере с тенью. Двумя основными прогнозами такого рода являются:

Проекция точки на плоскость или центральная проекция : Если $C$ — точка, называемая центром проекции , то проекция точки $P,$ отличной от $C$ , на плоскость, не содержащую $C,$ является пересечением прямой $CP$ с самолет. Точки $P$ , у которых линия $CP$ параллельна плоскости , не имеют никакого изображения в проекции, но часто говорят, что они проецируются в точку, находящуюся на бесконечности плоскости ( см. в Проективной геометрии формализацию этой терминологии ). Проекция самой точки $C$ не определена.
Проекция , параллельная направлению $D$ , на плоскость или параллельная проекция : Изображение точки $P$ — это пересечение плоскости с линией, параллельной $,$ проходящей через $P.$ D См. Аффинное пространство § Проекция для получения точного определения, обобщенного на любое измерение. ^{[ нужна ссылка ]}

Концепция проекции в математике очень старая и, скорее всего, уходит корнями в феномен теней, отбрасываемых объектами реального мира на землю. Эта элементарная идея была уточнена и абстрагирована сначала в геометрическом контексте, а затем и в других областях математики. Со временем развивались разные версии этой концепции, но сегодня, в достаточно абстрактной обстановке, мы можем объединить эти варианты. ^{[ нужна ссылка ]}

В картографии картографическая проекция — это карта части поверхности Земли на плоскость, что в ряде случаев, но не всегда, является ограничением проекции в указанном выше значении. также 3D-проекции лежат в основе теории перспективы . ^{[ нужна ссылка ]}

лежит необходимость объединения двух видов проекций и определения изображения посредством центральной проекции любой точки, отличной от центра проекции В основе проективной геометрии . Однако проективное преобразование — это биекция проективного пространства , свойство, не свойственное проекциям в этой статье. ^{[ нужна ссылка ]}

Определение [ править ]

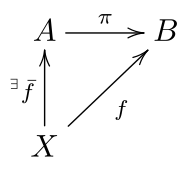
это универсальность проекции $π$ для любого отображения $f$ и множества $X.$ Коммутативность этой диаграммы —

Как правило, отображение, в котором домен и кодомен представляют собой один и тот же набор (или математическую структуру ), является проекцией, если отображение идемпотентно , что означает, что проекция равна своей композиции с самим собой. Проекция может также относиться к отображению, которое имеет правое обратное . Оба понятия тесно связаны следующим образом. Пусть $p$ — идемпотентное отображение множества $A$ в себя (таким образом, $p \circ p = p$ ), а $B = p (A)$ — образ $p$ . Если мы обозначим через $отображение$ p $,$ рассматриваемое как отображение $A$ на $B$ , а через $i —$ B вложение в $($ A $π$ так что $p = i \circ π$ ), то мы имеем $π \circ i = Id B$ (так что $π$ имеет правый обратный). И наоборот, если $π$ имеет правый обратный $i$ , то $из π \circ i = Id B$ следует, что $i \circ π \circ i \circ π = i \circ Id B \circ π = i \circ π$ ; то есть $p = i \circ π$ идемпотентно. ^{[ нужна ссылка ]}

Приложения [ править ]

Исходное понятие проекции было расширено или обобщено на различные математические ситуации, часто, но не всегда, связанные с геометрией, например:

В теории множеств :
- Операция, типичная для $j$ - ^й карта проекции , записанная $proj j$ , которая переводит элемент $x = (x 1, ..., x j, ..., x n)$ декартова произведения $X 1 \times \dots \times X j \times \dots \times X n$ к значению $проект j (Икс) знак равно Икс j .$ ^[1] Это отображение всегда сюръективно , и, когда каждое пространство $X k$ имеет топологию , оно также является непрерывным и открытым . ^[2]
- Отображение, которое переводит элемент в его класс эквивалентности при заданном отношении эквивалентности, известно как каноническая проекция . ^[3]
- Карта оценки отправляет функцию $f$ в значение $f (x)$ для фиксированного $x$ . Пространство функций $Y Х$ можно отождествить с декартовым произведением ${\textstyle \prod _{i\in X}Y}$ , а карта оценки представляет собой карту проекции декартова произведения. ^{[ нужна ссылка ]}
Для реляционных баз данных и языков запросов проекция записанная — это унарная операция, как $\Pi _{a_{1},\ldots ,a_{n}}(R)$ где $a_{1},\ldots ,a_{n}$ представляет собой набор имен атрибутов. Результат такого проектирования определяется как набор , который получается, когда все кортежи в $R$ ограничены набором $\{a_{1},\ldots ,a_{n}\}$ . ^[4]^[5]^[6]^{[ нужна проверка ]} $R$ — это отношение к базе данных . ^{[ нужна ссылка ]}
В сферической геометрии проекция сферы на плоскость использовалась Птолемеем (~150 г.) в его «Планисфаерии» . ^[7] Этот метод называется стереографической проекцией и использует плоскость, касающуюся сферы, и полюс C, диаметрально противоположный точке касания. Любая точка $P$ на сфере, кроме $C,$ определяет линию $CP$ , пересекающую плоскость в точке проекции $P$ . ^[8] Соответствие делает сферу одноточечной компактификацией плоскости, когда включена точка на бесконечности, соответствующая $C$ , которая в противном случае не имеет проекции на плоскость. Типичным примером является комплексная плоскость , где компактификация соответствует сфере Римана . Альтернативно, полушарие часто проецируется на плоскость с помощью гномонической проекции . ^{[ нужна ссылка ]}
В линейной алгебре — линейное преобразование , которое остаётся неизменным при двукратном применении: $p (u) = p (p (u))$ . Другими словами, идемпотентный оператор. Например, отображение, которое переносит точку $(x, y, z)$ в трех измерениях в точку $(x, y, 0)$ , является проекцией. Этот тип проекции естественным образом обобщается на любое число измерений $n$ для области и $k ⩽ n$ для кодобласти отображения. См. Ортогональная проекция , Проекция (линейная алгебра) . В случае ортогональных проекций пространство допускает разложение в произведение, и оператор проектирования также является проектором в этом смысле. ^[9]^[10]^{[ нужна проверка ]}
В дифференциальной топологии любой пучок волокон включает в себя карту проекции как часть своего определения. По крайней мере, локально эта карта выглядит как карта проекции в смысле топологии произведения и поэтому является открытой и сюръективной. ^{[ нужна ссылка ]}
В топологии ретракция — это непрерывное отображение $r : X \to X$ , которое ограничивается тождественным отображением на своем изображении. ^[11] Это удовлетворяет аналогичному условию идемпотентности $r 2 = r$ и может считаться обобщением карты проекции. Образ ретракции называется ретрактом исходного пространства. Ретракция, гомотопная тождеству, известна как деформационная ретракция . Этот термин также используется в теории категорий для обозначения любого расщепленного эпиморфизма. ^{[ нужна ссылка ]}
Скалярная проекция (или решающая) одного вектора на другой. ^{[ нужна ссылка ]}
В теории категорий приведенное выше понятие декартова произведения множеств может быть обобщено на произвольные категории . Произведение проекции некоторых объектов имеет канонический морфизм на каждый фактор. Этот прогноз будет принимать множество форм в разных категориях. Проекция из декартова произведения множеств и т . , топологии произведения топологических пространств (которая всегда сюръективна и открыта ) или из прямого произведения групп и даже д. Хотя эти морфизмы часто являются эпиморфизмами сюръективными, они не обязательно должны быть . ^[12]^{[ нужна проверка ]}

Ссылки [ править ]

^ «Прямое произведение — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.
^ Ли, Джон М. (2012). Введение в гладкие многообразия . Тексты для аспирантов по математике. Том. 218 (Второе изд.). п. 606. дои : 10.1007/978-1-4419-9982-5 . ISBN 978-1-4419-9982-5 . Упражнение А.32. Предполагать $X_{1},\ldots ,X_{k}$ являются топологическими пространствами. Докажите, что каждая проекция $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$ это открытая карта.
^ Браун, Арлен; Пирси, Карл (16 декабря 1994 г.). Введение в анализ . Springer Science & Business Media. ISBN 978-0-387-94369-5 .
^ Алагич, Суад (6 декабря 2012 г.). Технология реляционных баз данных . Springer Science & Business Media. ISBN 978-1-4612-4922-1 .
^ Дата, CJ (28 августа 2006 г.). Словарь реляционных баз данных: подробный глоссарий реляционных терминов и понятий с наглядными примерами . «О'Рейли Медиа, Инк.». ISBN 978-1-4493-9115-7 .
^ «Реляционная алгебра» . www.cs.rochester.edu . Архивировано из оригинала 30 января 2004 года . Проверено 29 августа 2021 г.
^ Сидоли, Натан; Берггрен, Дж.Л. (2007). «Арабская версия Планисферы Птолемея или Уплощение поверхности сферы: текст, перевод, комментарий» (PDF) . Скиамвс . 8 . Проверено 11 августа 2021 г.
^ «Стереографическая проекция — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.
^ «Проекция — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.
^ Роман, Стивен (20 сентября 2007 г.). Продвинутая линейная алгебра . Springer Science & Business Media. ISBN 978-0-387-72831-5 .
^ «Опровержение — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.
^ «Произведение семейства объектов в категории — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

Дальнейшее чтение [ править ]

Томас Крейг (1882) Трактат о прогнозах из коллекции исторической математики Мичиганского университета .

[1] «Прямое произведение — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

[2] Ли, Джон М. (2012). Введение в гладкие многообразия . Тексты для аспирантов по математике. Том. 218 (Второе изд.). п. 606. дои : 10.1007/978-1-4419-9982-5 . ISBN 978-1-4419-9982-5 . Упражнение А.32. Предполагать $X_{1},\ldots ,X_{k}$ являются топологическими пространствами. Докажите, что каждая проекция $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$ это открытая карта.

[3] Браун, Арлен; Пирси, Карл (16 декабря 1994 г.). Введение в анализ . Springer Science & Business Media. ISBN 978-0-387-94369-5 .

[4] Алагич, Суад (6 декабря 2012 г.). Технология реляционных баз данных . Springer Science & Business Media. ISBN 978-1-4612-4922-1 .

[5] Дата, CJ (28 августа 2006 г.). Словарь реляционных баз данных: подробный глоссарий реляционных терминов и понятий с наглядными примерами . «О'Рейли Медиа, Инк.». ISBN 978-1-4493-9115-7 .

[6] «Реляционная алгебра» . www.cs.rochester.edu . Архивировано из оригинала 30 января 2004 года . Проверено 29 августа 2021 г.

[7] Сидоли, Натан; Берггрен, Дж.Л. (2007). «Арабская версия Планисферы Птолемея или Уплощение поверхности сферы: текст, перевод, комментарий» (PDF) . Скиамвс . 8 . Проверено 11 августа 2021 г.

[8] «Стереографическая проекция — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

[9] «Проекция — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

[10] Роман, Стивен (20 сентября 2007 г.). Продвинутая линейная алгебра . Springer Science & Business Media. ISBN 978-0-387-72831-5 .

[11] «Опровержение — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

[12] «Произведение семейства объектов в категории — Математическая энциклопедия» . энциклопедияofmath.org . Проверено 11 августа 2021 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]