Гномоническая проекция

Гномоническая проекция , также известная как центральная проекция или прямолинейная проекция , представляет собой перспективную проекцию сферы касательную сферы с центром проекции в центре на любую плоскость , не проходящую через центр, чаще всего плоскость . При гномонической проекции каждый большой круг на сфере проецируется на прямую линию на плоскости (большой круг — это геодезическая на сфере, кратчайший путь между любыми двумя точками, аналог прямой линии на плоскости). ^[1] В более общем смысле, можно взять гномоническую проекцию любой $n$ -мерной гиперсферы на гиперплоскость .

Проекция — это $n$ -мерное обобщение тригонометрической касательной , которая отображает окружность в прямую линию, и, как и в случае с касательной, каждая пара противоположных точек на сфере проецируется в одну точку на плоскости, в то время как точки на плоскости плоскость, проходящая через центр сферы и параллельная плоскости изображения, проецируется в точки, находящиеся в бесконечности ; часто проекцию рассматривают как взаимно однозначное соответствие между точками полушария и точками плоскости, и в этом случае любая конечная часть плоскости изображения представляет собой часть полушария. ^[2]

Гномоническая проекция азимутальная (радиально-симметричная). В центре проецируемого изображения искажений формы не происходит, но искажения быстро возрастают по мере удаления от него.

Гномоническая проекция возникла в астрономии для построения солнечных часов и построения карты небесной сферы . Он обычно используется в качестве проекции географической карты и может быть удобен в навигации, поскольку курсы по большому кругу отображаются в виде прямых линий. Прямолинейные фотографические линзы создают перспективную проекцию мира на плоскость изображения; это можно рассматривать как гномоническую проекцию сферы изображения (абстрактная сфера, указывающая направление каждого луча, проходящего через камеру, смоделированную как точечное отверстие ). Гномоническая проекция используется в кристаллографии для анализа ориентации линий и плоскостей кристаллических структур. Он используется в структурной геологии для анализа ориентации плоскостей разломов. В компьютерной графике и компьютерном представлении сферических данных отображение куба — это гномоническая проекция сферы изображения на шесть граней куба .

В математике пространство ориентаций ненаправленных линий в трехмерном пространстве называется реальной проективной плоскостью и обычно изображается либо «проективной сферой», либо ее гномонической проекцией. Когда угол между линиями применяется как мера расстояния , это пространство называется эллиптической плоскостью . Гномоническая проекция 3-сферы единичных кватернионов , точки которой представляют собой 3-мерные вращения, приводит к векторам Родригеса . Гномоническая проекция двухлистного гиперболоида , рассматриваемая как модель гиперболической плоскости , называется моделью Бельтрами–Клейна .

История [ править ]

Гномоническая проекция считается старейшей картографической проекцией, предположительно приписываемой Фалесу , который, возможно, использовал ее для звездных карт в VI веке до нашей эры. ^[2] Путь кончика тени или светового пятна в солнечных часах, основанных на узле, прослеживает те же гиперболы, образованные параллелями на гномонической карте.

Свойства [ править ]

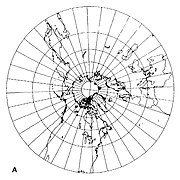
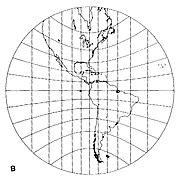
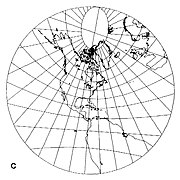
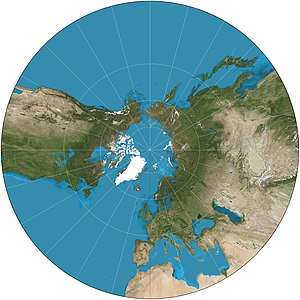
Гномоническая проекция осуществляется из центра сферы на плоскость, касательную к сфере (рис. 1 ниже). Сфера и плоскость соприкасаются в точке касания. Большие круги преобразуются в прямые линии с помощью гномонической проекции. Поскольку меридианы (линии долготы) и экватор представляют собой большие круги, на гномонической карте они всегда изображаются прямыми линиями. Поскольку проекция осуществляется из центра сферы, гномоническая карта может представлять менее половины площади сферы. Искажение масштаба карты увеличивается от центра (точки касания) к периферии. ^[2]

Если точка касания является одним из полюсов , то меридианы радиальные и расположены на одинаковом расстоянии друг от друга (рис. 2 ниже). Экватор невозможно показать, поскольку он бесконечен во всех направлениях. Остальные параллели (линии широты) изображаются в виде концентрических кругов .

Если точка касания находится на экваторе, то меридианы параллельны, но не на одинаковом расстоянии друг от друга (рис. 3 ниже). Экватор представляет собой прямую линию, перпендикулярную меридианам. Остальные параллели изображены в виде гипербол .

Если точка касания не находится на полюсе или экваторе, то меридианы представляют собой прямые линии, направленные наружу от полюса, но не на одинаковом расстоянии друг от друга (рис. 4 ниже). Экватор представляет собой прямую линию, перпендикулярную только одному меридиану, что указывает на то, что проекция не является конформной . Остальные параллели изображены в виде конических сечений .

Рис. 1. Большой круг проецируется на прямую в гномонической проекции.
Рис. 2. Гномоническая проекция с центром на северном полюсе.
Рис. 3. Гномоническая проекция с центром на экваторе.
Рис. 4. Гномоническая проекция с центром на 40° северной широты.

Как и во всех азимутальных проекциях, углы от точки касания сохраняются. Расстояние по карте от этой точки является функцией r ( d ) истинного расстояния d , определяемой формулой

r(d)=R\,\tan {\frac {d}{R}}

где R — радиус Земли. Радиальный масштаб

r'(d)={\frac {1}{\cos ^{2}{\frac {d}{R}}}}

и поперечный масштаб

{\frac {1}{\cos {\frac {d}{R}}}}

поэтому поперечный масштаб увеличивается внешне, а радиальный еще больше.

Используйте [ править ]

Гномонические проекции используются в сейсмических работах, поскольку сейсмические волны имеют тенденцию распространяться по большим кругам. Они также используются военно-морскими силами для определения пеленгации , поскольку радиосигналы распространяются по большим кругам. Метеоры также движутся по большим кругам: Gnomonic Atlas Brno 2000.0 является рекомендованным IMO набором звездных карт для визуальных наблюдений метеоров. Навигаторы самолетов и кораблей используют проекцию, чтобы найти кратчайший маршрут между пунктом отправления и пунктом назначения. Трек сначала рисуется на гномической карте, а затем переносится на карту Меркатора для навигации.

Гномоническая проекция широко используется в фотографии , где она называется прямолинейной проекцией , поскольку она естественным образом возникает из модели камеры-обскуры , где экран представляет собой плоскость. ^[3] Поскольку они эквивалентны, то же средство просмотра, которое используется для фотографических панорам, можно использовать для рендеринга гномонических карт ( просмотр в виде интерактивной панорамы на 360° ) .

Гномоническая проекция используется в астрономии, где точка касания центрируется на интересующем объекте. Проецируемая сфера в этом случае является небесной сферой R = 1, а не поверхностью Земли.

В астрономии гномические проекции звездных карт небесной сферы могут использоваться наблюдателями для точного построения прямой траектории метеорного следа . ^[4]

Сравнение гномонической проекции и некоторых азимутальных проекций с центром на 90 ° с.ш. в том же масштабе, упорядоченных по высоте проекции в радиусах Земли. (нажмите для подробностей)

См. также [ править ]

Местная касательная плоскость
Список картографических проекций
Модель Бельтрами – Клейна , аналогичное отображение гиперболической плоскости.

Ссылки [ править ]

^ Уильямс, CE; Ридд, МК (1960). «Большие круги и гномоническая проекция». Профессиональный географ . 12 (5): 14–16. дои : 10.1111/j.0033-0124.1960.125_14.x .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Снайдер, Джон П. (1987). Картографические проекции – Рабочее руководство . Профессиональный документ Геологической службы США. Том. 1395. Вашингтон, округ Колумбия: Типография правительства США. стр. 164–168. дои : 10.3133/pp1395 .
^ Пегораро, Винсент (12 декабря 2016 г.). Справочник по синтезу цифровых изображений: научные основы рендеринга . ЦРК Пресс. ISBN 978-1-315-39521-0 .
^ Тайби, Ричард (25 ноября 2016 г.), Чарльз Оливье и развитие метеорологии , Springer International Publishing, стр. 67, ISBN 9783319445182 .

Дальнейшее чтение [ править ]

Аморос, Хосе Луис; Бюргер, Мартин Дж.; Канут де Аморос, Мариса (1975). «3. Гномоническая проекция». Метод Лауэ . Академическая пресса. стр. 55–81. дои : 10.1016/B978-0-12-057450-6.50006-5 .
Калабретта, Марк Р.; Грейзен, Эрик В. (2002). «Представления небесных координат в FITS (Документ II)». Астрономия и астрофизика . 395 : 1077–1122. arXiv : astro-ph/0207413 . дои : 10.1051/0004-6361:20021327 .
Буке, Хендрик Энно (1913). Гномоническая проекция в ее применении к кристаллографическим задачам [ Гномоническая проекция в ее применении к кристаллографическим задачам ] (на немецком языке). Братья Борнтрегер.
Брэдли, AD (1940). «Гномоническая проекция сферы». Американский математический ежемесячник . 47 (10): 694–699. дои : 10.2307/2302492 . JSTOR 2302492 .
Де Морган, Август (1836). Объяснение гномонической проекции сферы . Болдуин и Крэдок.
Гюнтер, С. (1883). «Гномоническая картопроекция » Журнал Географического общества в Берлине (на немецком языке). 18 :137-149.
Герберт Смит, GF (1903). «О преимуществах гномической проекции и ее использовании при рисовании кристаллов» (PDF) . Минералогический журнал . 13 (62): 309–322. дои : 10.1180/minmag.1903.013.62.02 .
Хилтон, Гарольд (1904). «Гномоническая сеть» (PDF) . Минералогический журнал . 14 (63): 18–20. дои : 10.1180/minmag.1904.014.63.05 .
Палаш, Чарльз (1920). «Гномоническая проекция» (PDF) . Американский минералог . 5 (4): 67–80.
Пай, Норман (1950). «Наклонная гномоническая проекция». Обзор обзора империи . 10 (75): 227–232. дои : 10.1179/sre.1950.10.75.227 .
Роджерс, Остин Ф. (1907). «Гномоническая проекция с графической точки зрения» . Ежеквартальный журнал Горной школы . 29 (1): 24–33.

Внешние ссылки [ править ]