Пространственно-косая проекция Меркатора
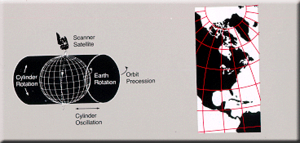
Космическая косая проекция Меркатора — это картографическая проекция, съемки Земли разработанная в 1970-х годах для подготовки карт на основе данных спутниковой . Это обобщение наклонной проекции Меркатора данного спутника , которое учитывает эволюцию во времени траектории движения для оптимизации ее представления на карте. Наклонная проекция Меркатора, с другой стороны, оптимизируется для заданной геодезической .
История
[ редактировать ]Пространственно-косая проекция Меркатора (SOM) была разработана Джоном П. Снайдером , Олденом Партриджем Колвокорессом и Джоном Л. Джанкинсом в 1976 году. Снайдер интересовался картами еще в детстве; он регулярно посещал картографические во время отпуска конференции. В 1972 году Геологической службе США (USGS) потребовалось разработать систему для уменьшения количества искажений, возникающих при спутниковых изображений эллипсоидной Земли печати на плоской странице. Колвокорессес, руководитель национальной картографической программы Геологической службы США, в 1976 году попросил участников конференции по геодезическим наукам помочь решить проблему проекции. [1] Снайдер поработал над проблемой с помощью своего недавно купленного карманного калькулятора и разработал математические формулы, необходимые для решения проблемы. Отправив свои расчеты Уолдо Тоблеру на проверку, Снайдер бесплатно передал их в Геологическую службу США. Впечатленные его работой, представители Геологической службы США предложили Снайдеру работу, и он сразу согласился. [1] Его формулы затем были использованы для создания карт со спутника Landsat 4 , запущенного летом 1978 года.
Описание проекции
[ редактировать ]Пространственно-наклонная проекция Меркатора обеспечивает непрерывное, почти конформное картографирование , полосы обзора воспринимаемой спутником. Масштаб верен вдоль наземной траектории и варьируется на 0,01 процента в пределах нормального диапазона обнаружения спутника. Соответствие соответствует диапазону чувствительности в пределах нескольких частей на миллион. Искажение по существу постоянное вдоль линий постоянного расстояния, параллельных путям пути. Пространственно-наклонная проекция Меркатора — единственная проекция, учитывающая вращение Земли.
Уравнения
[ редактировать ]Прямые уравнения косой проекции Меркатора для сферы выглядят следующим образом:
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Стоктон, Ник (20 июня 2014 г.). «Познакомьтесь с проекцией: косой Меркатор в пространстве» . Проводной.
- Джон Хесслер, Время проектирования: Джон Парр Снайдер и развитие косой проекции Меркатора в пространстве , Библиотека Конгресса, 2003 г.
- Статья Снайдера 1981 года, подробно описывающая вывод прогноза.
