Класс поликонической проекции

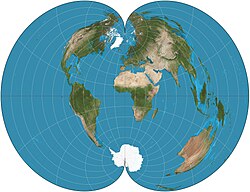
Поликоническая может относиться либо к классу картографических проекций , либо к конкретной проекции, менее двусмысленно известной как американская поликоническая проекция . Поликонические как класс относятся к тем проекциям, параллелями которых являются все неконцентрические дуги окружностей, за исключением прямого экватора, а центры этих окружностей лежат вдоль центральной оси. Это описание применимо к проекциям в экваториальном аспекте. ^[1]

Поликонические проекции

Некоторые из проекций, которые попадают в поликонический класс:

Американская поликоническая проекция - каждая параллель становится дугой окружности, имеющей истинный масштаб, тот же масштаб, что и центральный меридиан.
Широтно-равнодифференциальная поликоническая проекция
Прямоугольная поликоническая проекция
Проекция Ван дер Гринтена — проецирует всю Землю в один круг; все меридианы и параллели представляют собой дуги окружностей.
Шаровидная проекция Николози — обычно используется для проецирования полушария в круг; все меридианы и параллели представляют собой дуги окружностей. ^[2]

Серию поликонических проекций, каждая по кругу, также представил Ганс Мауэр в 1922 году. ^[3] который также представил равновеликий поликон в 1935 году. ^[4]^: 248 Еще одна серия Георгия Александровича Гинзбурга появилась начиная с 1949 года. ^[4]^{: 258–262}

Большинство поликонических проекций, используемых для картирования всей сферы, создают карту мира в форме «яблока».Существует множество проекций в форме «яблока», почти все они неясны. ^[2]

См. также

Список картографических проекций

Ссылки

^ Альбом картографических проекций (Профессиональный документ Геологической службы США 1453), Джон П. Снайдер и Филип М. Воксланд, 1989, стр. 4.
^ Перейти обратно: ^а ^б Джон Дж. Г. Савард. «Проекция Дитриха-Китады» .
^ https://pubs.usgs.gov/pp/1453/report.pdf. ^{[ пустой URL PDF ]}
^ Перейти обратно: ^а ^б Джон П. Снайдер (1993). Выравнивание Земли: две тысячи лет картографических проекций . ISBN 0-226-76747-7 .

Внешние ссылки

Таблица примеров и свойств всех распространенных проекций с сайта радикалакартографии.нет.

Эта картографии или картографии статья о незавершена . Вы можете помочь Википедии, расширив ее .

[1] Альбом картографических проекций (Профессиональный документ Геологической службы США 1453), Джон П. Снайдер и Филип М. Воксланд, 1989, стр. 4.

[savard-2] Перейти обратно: ^а ^б Джон Дж. Г. Савард. «Проекция Дитриха-Китады» .

[3] ttps://pubs.usgs.gov/pp/1453/report.pdf. ^{[ пустой URL PDF ]}

[Flattening-4] Перейти обратно: ^а ^б Джон П. Снайдер (1993). Выравнивание Земли: две тысячи лет картографических проекций . ISBN 0-226-76747-7 .

[1]

[2]

[3]

[4]