Локсимутальная проекция
Эта статья нуждается в дополнительных цитатах для проверки . ( февраль 2019 г. ) |
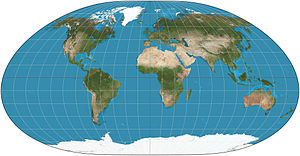
В картографии локсимутальная проекция — это картографическая проекция, введенная Карлом Симоном в 1935 году и независимо в 1966 году Уолдо Р. Тоблером, который дал ей название. [1] Характеризуется тем , что локсодромы (прямые линии) от одной выбранной центральной точки (пересечение центрального меридиана и центральной широты ) показаны прямыми линиями, правильными по азимуту от центра и «соответствующими масштабу» в смысле что расстояния, измеренные по таким линиям, пропорциональны длинам соответствующих румбических линий на поверхности Земли. Это не равновеликая и не равновеликая проекция .
Описание
[ редактировать ]Локсодрома на поверхности Земли представляет собой кривую постоянного направления: она пересекает все параллели широты под одним и тем же углом. Предположим, что его пеленг — θ к северу от востока, поэтому, например, направление на восток — θ = 0; на севере θ = прямой угол; на западе составляет θ = полукруг. Полная длина локсодрома, идущая от южного полюса к северному полюсу, обычно рассматривается как π R csc θ, где R - радиус Земли (в частности, если локсодром идет прямо на восток, он обходит Землю бесконечно много раз). не приближаясь ни к одному из полюсов, поэтому его длина равна ∞. Пусть локсодром проходит через точку, долгота и широта которой равны 0; назовите ее «центральной точкой». в определенном направлении вдоль этого локсодрома и достигает географического местоположения. Пусть f ( p ) — точка в плоскости ( x , y ). ), до которой можно добраться, пройдя то же расстояние в том же направлении от начала координат (0, 0). Таким образом, f ( p ) ∈ R × [− π R / 2 , π R / 2 ]. Эта точка f ( p ) является изображением точки p на карте. идет более одного локсодрома От центральной точки до p , но есть единственный самый короткий: тот, который не пересекает меридиан 180° на своем пути от центральной точки до p . Если включить локсодромы, пересекающие меридиан 180°, то получится бесконечно много изображений всей Земли, занимающих всю полосу R × [− π R / 2 , π R / 2 ]. Использование только единственного кратчайшего локсодрома от центральной точки до каждой точки p дает только одну копию, занимающую своего рода овал.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Снайдер, Джон П .; Воксленд, Филип М. (1989). «Альбом картографических проекций». Альбом картографических проекций (PDF) . Профессиональный документ Геологической службы США 1453. Вашингтон, округ Колумбия: Типография правительства США. стр. 90, 223. doi : 10.3133/pp1453 . Проверено 18 февраля 2019 г.