Двухточечная эквидистантная проекция
Двухточечная равноотстоящая проекция или дважды равноотстоящая проекция — это картографическая проекция, впервые описанная Гансом Маурером в 1919 году и Чарльзом Клоузом в 1921 году. [1] [2] Это обобщение гораздо более простой азимутальной эквидистантной проекции . В этой двухточечной форме локуса картограф выбирает две точки для настройки проекции. Расстояния от двух локусов до любой другой точки на карте верны: то есть они масштабируются до расстояний до тех же точек на сфере.
Двухточечная эквидистантная проекция отображает семейство софокусных сферических коник на два семейства плоских эллипсов и гипербол. [3]
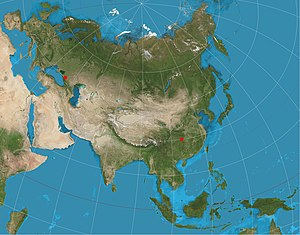
Проекция использовалась для всех карт Азиатского континента в атласах Национального географического общества с 1959 года. [4] хотя в данном случае его целью было уменьшить искажения по всей Азии, а не проводить измерения по двум локусам. [5] Проекция иногда появляется на картах воздушных маршрутов. является Триметрическая проекция Чемберлина логическим расширением идеи двух точек до трех точек, но случай трех точек дает лишь своего рода минимальную ошибку для расстояний от трех локусов, а не дает правильные расстояния. Тоблер распространил эту идею на произвольно большое количество локусов, используя автоматизированные методы среднеквадратичной минимизации вместо использования формул закрытой формы . [6]
Проекцию можно обобщить до эллипсоида вращения, используя геодезическое расстояние. [7]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Ганс Маурер (1919). «Двухлучевая, ортодромная», а не «двухазимутальная, гномоническая» конструкция карты. Картограммы с двойным центральным расстоянием. (Заметки к эссе В. Иммлера и Х. Торада. Ann. d. Hydr. и др. 1919, стр. 22 и 35.), Annals of Hydroography and Maritime Meteorology , 47 (3–4), 75–8.
- ^ Чарльз Клоуз (1921). «Обратите внимание на дважды равноотстоящую проекцию». Географический журнал 57 (6), 446–448. https://www.jstor.org/stable/1780793
- ^ Дж. Ф. Кокс (1946) «Дважды равноотстоящая проекция». Бык. Геодезика 2, 74–76. https://doi.org/10.1007/BF02521618
- ^ Снайдер, JP (1993). Сплющивание Земли: 2000 лет картографических проекций . стр. 234–235. ISBN 0226767469 .
- ^ «Портрет крупнейшего континента Земли», журнал National Geographic , вып. 116, нет. 6, с. 751, 1959 г.
- ^ Тоблер, Уолдо (апрель 1986 г.). «Измерение сходства картографических проекций» . Картография и географическая информатика . 13 (2): 135–139. doi : 10.1559/152304086783900103 – через Researchgate.
- ^ Чарльз Карни, (2011). «Геодезика на эллипсоиде вращения». https://arxiv.org/abs/1102.1215
- Чарльз Клоуз (1934). «Дважды равноудалённая проекция сферы». Географический журнал 83 (2): 144–145.
- Чарльз Клоуз (1947). Географические обходные пути: и некоторые другие географические очерки. Э. Арнольд.
- Уолдо Р. Тоблер (1966). «Заметки о двух прогнозах». Картографический журнал 3 (2). 87–89.
- Франсуа Рейнье (1957). Проекционные системы и их приложения в географии, картографии, навигации, топометрии и др. Национальный географический институт.
 | Эта картографии или картографировании статья о незавершена . Вы можете помочь Википедии, расширив ее . |