Цилиндрическая равновеликая проекция

Ламберта цилиндрическая равновеликая проекция мира; стандартная параллель под углом 0°

Цилиндрическая равновеликая проекция Ламберта (стандартная параллель под углом 0°, нормальная) с Тиссо . индикатрисой деформации

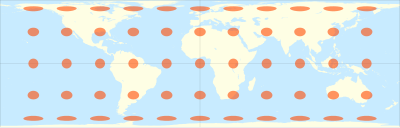
В картографии нормальная цилиндрическая равновеликая проекция представляет собой семейство цилиндрических нормальных равной площади картографических проекций .

История

Изобретение равновеликой цилиндрической проекции Ламберта приписывается швейцарскому математику Иоганну Генриху Ламберту в 1772 году. Его вариации появлялись на протяжении многих лет изобретателями, которые увеличивали высоту Ламберта и соразмерно сжимали ширину в различных соотношениях.

Описание

Как Земля проецируется на цилиндр

Проекция:

• цилиндрический . , то есть имеет цилиндрическую проекционную поверхность
• нормально, это означает, что у него нормальный аспект
• — это проекция равной площади, то есть любые две области на карте имеют одинаковый относительный размер по сравнению с их размером на сфере.

Термин «нормальная цилиндрическая проекция» используется для обозначения любой проекции, в которой меридианы отображаются на равноотстоящих друг от друга вертикальных линиях, а круги широты отображаются на горизонтальные линии (или, mutatis mutandis , в более общем смысле, отображаются радиальные линии от фиксированной точки). параллельные линии, расположенные на равном расстоянии друг от друга, а концентрические окружности вокруг них отображаются в перпендикулярные линии).

Сопоставление меридианов с вертикальными линиями можно визуализировать, представив цилиндр, ось которого совпадает с осью вращения Земли, затем проецируя его на цилиндр и впоследствии разворачивая цилиндр.

По геометрии своей конструкции цилиндрические выступы простираются на расстояния с востока на запад. Величина растяжения одинакова на любой выбранной широте во всех цилиндрических проекциях и определяется секущей широты , кратной масштабу экватора. Различные цилиндрические проекции отличаются друг от друга исключительно своим простиранием с севера на юг (где широта определяется φ ):

Единственные нормальные цилиндрические выступы, которые сохраняют площадь, имеют сжатие с севера на юг, обратное растяжению с востока на запад ( cos   φ ). Это делит расстояния с севера на юг на коэффициент, равный секущей широты, сохраняя площадь, но искажая формы.

Шкала восток-запад, соответствующая шкале север-юг.

В зависимости от коэффициента растяжения S любая конкретная цилиндрическая проекция равной площади имеет нулевую, одну или две широты, для которых масштаб восток-запад соответствует масштабу север-юг.

• S>1: ноль
• S=1: первая, эта широта — экватор.
• S<1: пара одинаковых широт противоположного знака.

Формулы

Формулы предполагают сферическую модель и используют следующие определения:

• λ - долгота
• λ ₀ – центральный меридиан
• φ — широта
• φ ₀ — стандартная широта
• S — коэффициент растяжения
• x — горизонтальная координата проецируемого местоположения на карте.
• y — вертикальная координата проецируемого местоположения на карте.

	используя стандартную широту φ 0	с использованием коэффициента растяжения S	S=1, φ0 0 =
используя радианы	${\begin{aligned}x&=\cos \varphi _{0}(\lambda -\lambda _{0})\\y&={\frac {\sin \varphi }{\cos \varphi _{0}}}\end{aligned}}$	${\begin{aligned}x&={\sqrt {S}}(\lambda -\lambda _{0})\\y&={\frac {\sin \varphi }{\sqrt {S}}}\end{aligned}}$	${\begin{aligned}x&=\lambda -\lambda _{0}\\y&=\sin \varphi \end{aligned}}$
используя градусы	${\begin{aligned}x&={\frac {\cos \varphi _{0}\pi (\lambda -\lambda _{0})}{180^{\circ }}}\\y&={\frac {\sin \varphi }{\cos \varphi _{0}}}\end{aligned}}$	${\begin{aligned}x&={\frac {{\sqrt {S}}\pi (\lambda -\lambda _{0})}{180^{\circ }}}\\y&={\frac {\sin \varphi }{\sqrt {S}}}\end{aligned}}$	${\begin{aligned}x&={\frac {\pi (\lambda -\lambda _{0})}{180^{\circ }}}\\y&=\sin \varphi \end{aligned}}$

Отношения между $S$ и $\varphi _{0}$:

• $S=\cos ^{2}\varphi _{0}$
• $\varphi _{0}=\arccos {\sqrt {S}}$

Специализации

Специализации различаются только соотношением вертикальной и горизонтальной оси. Некоторые специализации были описаны, продвинуты или названы иным образом.

Специализации нормальной цилиндрической равновеликой проекции, изображения, показывающие проекцию с центром на Гринвичском меридиане.

Фактор растяжения С	Соотношение сторон (ширина-высота) п С	Стандартная параллель(и) ж 0	Изображение (индикатриса Тиссо)	Изображение (Синий мрамор)	Имя	Издатель	Год издания
1	π ≈ 3,142	0°			Ламберта цилиндрический равновеликий	Иоганн Генрих Ламберт	1772
⁠ 3 / 4 ⁠ = 0.75	⁠ 3 π / 4 ⁠ ≈ 2.356	30°			Берманн	Вальтер Берманн	1910
⁠ 2 / π ⁠ ≈ 0.6366	2	$\arccos {\sqrt {\tfrac {2}{\pi }}}$ ≈ 37°04 ′ 17″ ≈ 37.0714°			Смит равноповерхностный = Крастер прямоугольный	Чарльз Пьяцци Смит	1870
потому что 2 (37.4°) ≈ 0.6311	π · соз 2 (37.4°) ≈ 1.983	37°24 ′ = 37.4°			Тристан Эдвардс	Тристан Эдвардс	1953
потому что 2 (37.5°) ≈ 0.6294	π · соз 2 (37.5°) ≈ 1.977	37°30 ′ = 37.5°			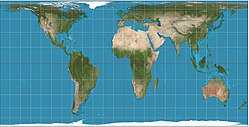Хобо-Дайер	Мик Дайер	2002
потому что 2 (40°) ≈ 0.5868	π · соз 2 (40°) ≈ 1.844	40°			(безымянный)
⁠ 1 / 2 ⁠ =0.5	⁠ π / 2 ⁠ ≈ 1.571	45°			Галл – Питерс = Галл орфографический = Питерс	Джеймс Галл , Продвигается Арно Петерсом как его собственное изобретение.	1855 (Кан), 1967 (Питерс)
потому что 2 (50°) ≈ 0.4132	π · соз 2 (50°) ≈ 1.298	50°			Бальтасар	М. Бальтасар	1935
⁠ 1 / π ⁠ ≈ 0.3183	1	$\arccos {\sqrt {\tfrac {1}{\pi }}}$ ≈ 55°39 ′ 14″ ≈ 55.6540°		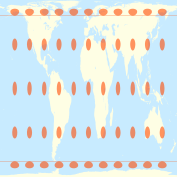	Мир Тоблера в квадрате	Уолдо Тоблер	1986

Производные

, Гиперэллиптическая проекция Тоблера впервые описанная Тоблером в 1973 году, является дальнейшим обобщением семейства цилиндрических равновеликих проекций.

Проекция HEALPix представляет собой равновеликую гибридную комбинацию: цилиндрической равновеликой проекции Ламберта для экваториальных областей сферы; и прерывистая проекция Коллиньона для полярных регионов.

Внешние ссылки

• Таблица примеров и свойств всех распространенных проекций с сайта радикалакартографии.нет.