Проекция Робинсона

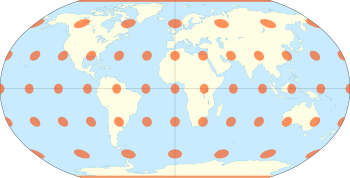

Проекция Робинсона — это картографическая проекция карты мира , которая показывает весь мир одновременно. Он был специально создан в попытке найти хороший компромисс с проблемой быстрого отображения всего земного шара в виде плоского изображения. [1]
Проекция Робинсона была разработана Артуром Х. Робинсоном в 1963 году в ответ на обращение компании Rand McNally , которая с тех пор использовала эту проекцию на картах мира общего назначения. Робинсон опубликовал подробности построения проекции в 1974 году. Национальное географическое общество (NGS) начало использовать проекцию Робинсона для карт мира общего назначения в 1988 году, заменив проекцию Ван дер Гринтена . [2] В 1998 году NGS отказалась от проекции Робинсона в пользу трипельной проекции Винкеля , поскольку последняя «уменьшает искажение массивов суши по мере их приближения к полюсам». [3] [4]
Сильные и слабые стороны
[ редактировать ]Проекция Робинсона не является ни равновеликой, ни равноугольной , поэтому приходится отказываться от обоих в пользу компромисса. Создатель считал, что это создаст лучший общий вид, чем можно было бы достичь, придерживаясь любого из них. Меридианы плавно изгибаются, избегая крайностей, но тем самым вытягивают полюса в длинные линии, а не оставляют их точками. [1]
Следовательно, искажения вблизи полюсов являются серьезными, но при удалении от них быстро снижаются до умеренного уровня. Прямые параллели подразумевают сильное угловое искажение на высоких широтах по направлению к внешним краям карты – недостаток, присущий любой псевдоцилиндрической проекции. Однако на момент разработки проекция эффективно соответствовала цели Рэнда МакНелли создать привлекательные изображения всего мира. [5] [6]
Я решил пойти по этому пути задом наперед. … Я начал с своего рода художественного подхода. Я визуализировал самые красивые формы и размеры. Я работал с переменными до тех пор, пока не дошёл до того, что если я изменю одну из них, то лучше не станет. Затем я придумал математическую формулу, позволяющую добиться такого эффекта. Большинство картографов начинают с математики.
- , 1988 г. в New York Times Статья [1]
Формулировка
[ редактировать ]Проекция определяется таблицей: [7] [8] [9]
| Широта | Х | И |
|---|---|---|
| 0° | 1.0000 | 0.0000 |
| 5° | 0.9986 | 0.0620 |
| 10° | 0.9954 | 0.1240 |
| 15° | 0.9900 | 0.1860 |
| 20° | 0.9822 | 0.2480 |
| 25° | 0.9730 | 0.3100 |
| 30° | 0.9600 | 0.3720 |
| 35° | 0.9427 | 0.4340 |
| 40° | 0.9216 | 0.4958 |
| 45° | 0.8962 | 0.5571 |
| 50° | 0.8679 | 0.6176 |
| 55° | 0.8350 | 0.6769 |
| 60° | 0.7986 | 0.7346 |
| 65° | 0.7597 | 0.7903 |
| 70° | 0.7186 | 0.8435 |
| 75° | 0.6732 | 0.8936 |
| 80° | 0.6213 | 0.9394 |
| 85° | 0.5722 | 0.9761 |
| 90° | 0.5322 | 1.0000 |
Таблица индексирована по широте с интервалом в 5 градусов; промежуточные значения рассчитываются с помощью интерполяции . Робинсон не указал какой-либо конкретный метод интерполяции, но сообщается, что другие использовали либо интерполяцию Эйткена (с полиномами неизвестной степени), либо кубические сплайны при анализе деформации площади в проекции Робинсона. [10] Столбец X — отношение длины параллели к длине экватора; столбец Y можно умножить на 0,2536 [11] чтобы получить отношение расстояния этой параллели от экватора к длине экватора. [7] [9]
Координаты точек на карте вычисляются следующим образом: [7] [9]
где R — радиус земного шара в масштабе карты, λ — долгота точки для построения, а λ 0 — центральный меридиан, выбранный для карты (как λ, так и λ 0 выражаются в радианах ).
Простые следствия этих формул:
- Поскольку x вычисляется как постоянный множитель меридиана по всей параллели, меридианы долготы, таким образом, располагаются на одинаковом расстоянии вдоль параллели.
- Поскольку у не зависит от долготы, параллели представляют собой прямые горизонтальные линии.
Приложения
[ редактировать ]Центрального разведывательного управления Мировая книга фактов использует проекцию Робинсона в своих политических и физических картах мира.
Европейский центр профилактики и контроля заболеваний рекомендует использовать проекцию Робинсона для картографирования всего мира. [12]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б с Джон Ноубл Уилфорд (25 октября 1988 г.). «Невозможный поиск идеальной карты» . Нью-Йорк Таймс . Проверено 1 мая 2012 г.
- ^ Снайдер, Джон П. (1993). Выравнивание Земли: 2000 лет картографических проекций . Издательство Чикагского университета. п. 214. ИСБН 0226767469 .
- ^ «Карты National Geographic – Настенные карты – Мировая классика (увеличенная)» . Национальное географическое общество . Проверено 17 февраля 2019 г.
На этой карте используется проекция Винкеля Трипеля, позволяющая уменьшить искажение массивов суши по мере их приближения к полюсам.
- ^ «Выбор картографической проекции» . Национальное географическое общество . Проверено 17 февраля 2019 г.
- ^ Мирна Оливер (17 ноября 2004 г.). «Артур Х. Робинсон, 89 лет; картографа хвалят за эллиптический дизайн карты» . Лос-Анджелес Таймс . Проверено 1 мая 2012 г.
- ^ Служба новостей New York Times (16 ноября 2004 г.). «Артур Х. Робинсон, 89 лет. Географ улучшил карту мира» . Чикаго Трибьюн . Проверено 1 мая 2012 г.
- ^ Jump up to: а б с Ипбукер, К. (июль 2005 г.). «Вычислительный подход к проекции Робинсона» . Обзор опроса . 38 (297): 204–217. дои : 10.1179/sre.2005.38.297.204 . S2CID 123437786 . Проверено 17 февраля 2019 г.
- ^ «Таблица построения проекции Робинсона» . RadicalCartography.net . Проверено 17 февраля 2019 г.
- ^ Jump up to: а б с Снайдер, Джон П .; Воксленд, Филип М. (1989). Альбом картографических проекций (PDF) . Профессиональный документ Геологической службы США 1453. Вашингтон, округ Колумбия: Типография правительства США. стр. 82–83, 222–223. дои : 10.3133/pp1453 . Проверено 4 февраля 2022 г.
- ^ Ричардсон, Роберт Т. (1989). «Деформация площади по проекции Робинсона» . Американский картограф . 16 (4): 294–296. дои : 10.1559/152304089783813936 .
- ^ По формулам ниже это можно рассчитать как .
- ^ Европейский центр профилактики и контроля заболеваний. (2018). Рекомендации по представлению данных эпиднадзора: таблицы, графики, карты . ЛУ: Офис публикаций. дои : 10.2900/452488 .
Дальнейшее чтение
[ редактировать ]- Артур Х. Робинсон (1974). «Новая картографическая проекция: ее развитие и характеристики». В: Международный ежегодник картографии . Том 14, 1974, стр. 145–155.
- Джон Б. Гарвер младший (1988). «Новый взгляд на мир». В: National Geographic , декабрь 1988 г., стр. 911–913.
- Джон П. Снайдер (1993). Сплющивание Земли — 2000 лет картографических проекций , Издательство Чикагского университета. стр. 214–216.
Внешние ссылки
[ редактировать ]- Таблица примеров и свойств всех распространенных проекций с сайта радикалакартографии.нет.
- Численная оценка проекции Робинсона , из книги «Картография и географическая информатика», апрель 2004 г., автор Ченгижан Ипбукер.

