Проекция полушария в квадрате Гую

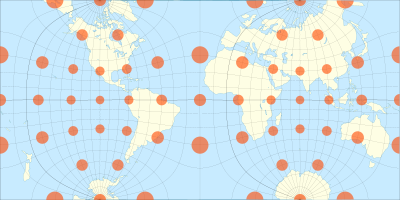
Проекция Гуйю «полушарие в квадрате» — это конформная картографическая проекция полушария. Это косой аспект квинкунциальной проекции Пирса .
История
[ редактировать ]Проекция была разработана Эмилем Гюю из Франции в 1887 году. [1] [2]
Формальное описание
[ редактировать ]Проекцию можно вычислить как косой аспект квинкунциальной проекции Пирса, повернув ось на 45 градусов. Его также можно вычислить, повернув координаты на -45 градусов перед вычислением стереографической проекции; затем эта проекция преобразуется в квадрат, координаты которого затем поворачиваются на 45 градусов. [3]
Проекция конформная, за исключением четырех углов квадрата каждого полушария. Как и другие конформные многоугольные проекции, Гуйу является отображением Шварца-Кристофеля .
Характеристики
[ редактировать ]Его свойства очень похожи на свойства квинкунциальной проекции Пирса :
- Каждое полушарие представлено в виде квадрата, сфера — в виде прямоугольника с соотношением сторон 2:1.
- Та часть, где преувеличение масштаба вдвое превышает размер в центре каждого квадрата, составляет всего 9% площади сферы, против 13% для Меркатора и 50% для стереографического. [4]
- Кривизна линий, изображающих большие круги, в каждом случае очень незначительна на большей части их длины. [4]
- Он конформен везде, за исключением углов квадрата, соответствующего каждому полушарию, где два меридиана дважды резко меняют направление; Экватор представлен горизонтальной линией.
- Его можно разметить во всех направлениях.
Связанные прогнозы
[ редактировать ]- Проекция полушария Адамса в квадрате и квинкунциальная проекция Пирса являются разными аспектами одного и того же основного отображения Шварца – Кристоффеля. Такие отображения представляют собой преобразования половины стереографической проекции .
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Э. Гую (1887) «Новая система проекции сферы: обобщение проекции Меркатора», Annals Hydrographiques, Ser. 2, Том. 9, 16–35. https://www.retronews.fr/journal/annales-гидрографики/1-январь-1887/1877/4868382/23
- ^ Снайдер, Джон П. (1993). Уплощение Земли . Чикагский университет. ISBN 0-226-76746-9 .
- ^ Л. П. Ли (1976). «Конформные проекции на основе эллиптических функций» . Картографика . 13 (Монография 16, приложение № 1 к «Канадскому картографу»).
- ^ Jump up to: а б К.С. Пирс (декабрь 1879 г.). «Квинкунциальная проекция сферы». Американский журнал математики . 2 (4). Издательство Университета Джонса Хопкинса: 394–396. дои : 10.2307/2369491 . JSTOR 2369491 .