Триангуляция (съемка)

При наблюдении , триангуляция - это процесс определения местоположения точки путем измерения только углов по ней по известным точкам на любом конце фиксированной базовой линии с использованием тригонометрии , а не измерения расстояний до точки непосредственно, как в трилатерации . Затем эта точка может быть зафиксирована как третья точка треугольника с одной известной стороной и двумя известными углами.

Триангуляция также может относиться к точному обзору систем очень больших треугольников, называемых триангуляционными сетями . Это последовало за работой Виллеброрда Снелла в 1615–17 годах, который показал, как точка может быть расположена с угла, поднятых из трех известных точек, но измеренная в новой неизвестной точке, а не в ранее фиксированных точках, возникает проблема, называемая резекцией . Ошибка наблюдения сводится к минимуму, если сначала установлена сетка треугольников по самой большой соответствующей шкале. Точки внутри треугольников могут быть точно расположены со ссылкой на него. Такие методы триангуляции были использованы для точного крупномасштабного обзора земли до роста глобальных спутниковых систем навигации в 1980-х годах.

Принцип

Траунгуляция может использоваться для поиска позиции корабля, когда известны позиции A и B. Наблюдатель в A измеряет угол α , в то время как наблюдатель в B измеряет β .

Положение любой вершины треугольника может быть рассчитана, если известно положение одной стороны и два угла. Следующие формулы строго верны только для плоской поверхности. Если должна быть разрешена кривизна Земли, то сферическая тригонометрия должна использоваться .

Расчет

С $\ell$ Быть расстоянием между A и B дает:

\ell ={\frac {d}{\tan \alpha }}+{\frac {d}{\tan \beta }}

Используя тригонометрические идентичности tan a = sin a / cos a и sin (a + b) = sin a cos b + cos a sin b, это эквивалентно:

\ell =d\left({\frac {\cos \alpha }{\sin \alpha }}+{\frac {\cos \beta }{\sin \beta }}\right)

\ell =d\ {\frac {\sin(\alpha +\beta )}{\sin \alpha \sin \beta }}

поэтому:

d=\ell \ {\frac {\sin \alpha \sin \beta }{\sin(\alpha +\beta )}}

Исходя из этого, легко определить расстояние неизвестной точки от любой точки наблюдения, его север/юг и восток/запад от точки наблюдения и, наконец, его полные координаты.

История

Триангуляционная сеть девятнадцатого века для триангуляции Рейнленд-Хессе

Триангуляция сегодня используется для многих целей, включая съемки , навигацию , метрологию , астрометрию , бинокулярное зрение , модель ракетинга и направление оружия оружия .

В этой области методы триангуляции, по -видимому, не использовались римскими специалистами земли, агрозри ; но были введены в средневековую Испанию через арабские трактаты об астролябе , например, Ибн аль-Саффар (ум. 1035). ^{[ 1 ]} Абу Райхан Бируни (ум. 1048) также ввел методы триангуляции, чтобы измерить размер земли и расстояния между различными местами. ^{[ 2 ]} Похоже, что упрощенные римские методы, по-видимому, сосуществовали с более сложными методами, используемыми профессиональными геодезистами. Но редко для перевода таких методов на латынь (руководство по геометрии, геоматрия auctoris одиннадцатого века - редкое исключение), и такие методы, по -видимому, просачивались лишь медленно в остальную часть Европы. ^{[ 1 ]} Повышенная осведомленность и использование таких методов в Испании могут быть подтверждены средневековыми сотрудниками Иакова , используемые специально для измерения углов, которые датируются примерно 1300; и появление точно обследованных береговых линий в портоланских картах , самое раннее из которых выживает, датируется 1296.

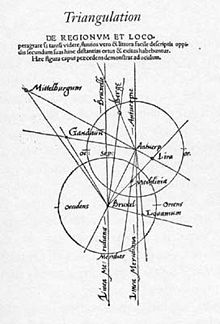
Джемма Фризиус

На суше картограф Джемма Фризиус далекие места для создания карт в своей премьерной форме 1533 предложила использовать триангуляцию, чтобы точно позиционировать . года Издание Питера Апиана бестселлеров 1524 Cosmographica . Это стало очень влиятельным, и техника распространилась по всей Германии, Австрии и Нидерландам. Астроном Тайчо Брахе применил метод в Скандинавии, завершив подробную триангуляцию в 1579 году на острове Хвена , где была основана его обсерватория, со ссылкой на ключевые достопримечательности с обеих сторон Орундов , создавая план поместья острова в 1584 году. ^{[ 3 ]} В Англии Метод Фризиуса был включен в растущее число книг, посвященных съемкам, которые появились начиная с середины века, в том числе Уильяма Кунингема ( космографический гладс 1559), трактат Валентин Ли из измерения всех видов земель (1562), Уильям Борн, Уильям Борн, Уильям Борн, Уильям Борн, Уильям Борн Правила навигации (1571), геометрическая практика Томаса Дигжеса по имени Пантометрия (1571) и Джон ( Нордена Диалог геодезиста 1607). Было высказано предположение, что Кристофер Сакстон, возможно, использовал грубую и готовую триангуляцию, чтобы разместить особенности на картах его округа 1570-х годов; Но другие предполагают, что, получив грубые подшипники с функциями с ключевых точек Vantage, он, возможно, оценил расстояния для них просто с помощью догадков. ^{[ 4 ]}

Виллеброрд Снелл

Современное систематическое использование триангуляционных сетей обусловлено работой голландского математика Виллебрда Снелла , который в 1615 году обследовал расстояние от Алкмаара до Бреда , приблизительно 72 мили (116 километров), используя цепь из четырехугольников, содержащих 33 треугольника. Снелл недооценил расстояние на 3,5%. Два города были разделены одной степенью на Меридиане , поэтому из -за его измерения он смог рассчитать ценность для окружности Земли - подвиг, отмеченный в названии его книги Эратостена Батавуса ( голландские эратостенесы ), опубликованный в 1617 году. .. Он также показал, как резекция или рассчитать положение точки внутри треугольника, используя углы, отлитые между вершинами в неизвестной точке. Они могут быть измерены гораздо точнее, чем подшипники вершин, которые зависели от компаса. Это установило ключевую идею обследования крупномасштабной первичной сети контрольных точек, а затем определить местонахождение вторичных вспомогательных точек позже, в этой первичной сети.

Дальнейшие события

Методы Снелла были приняты Джин Пикард , который в 1669–70 годах обследовал одну степень широты вдоль Парижа Меридиана, используя цепь из тринадцати треугольников, простирающихся к северу от Парижа до часовой шахты Сурдона , недалеко от Амиенса . Благодаря улучшениям в инструментах и точности, Пикард оценивается как первое достаточно точное измерение радиуса Земли. В течение следующего столетия эта работа была продлена, наиболее заметной семьей Кассини: между 1683 и 1718 годами Жан-Доминик Кассини и его сын Жак Кассини обследовали весь Париж Меридиан от Дюнкерка до Перпиньяна ; и между 1733 и 1740 годами Жак и его сын Сесар Кассини предприняли первую триангуляцию всей страны, включая переосмысление меридианской дуги , что привело к публикации в 1745 году первой карты Франции, созданной по строгим принципам.

Методы триангуляции к настоящему времени были хорошо известны для местных карт, но только к концу 18 -го века другие страны начали создавать подробные обследования сети триангуляции для картирования целых стран. Основная триангуляция Великобритании была начата в результате исследования боеприпасов в 1783 году, хотя и не завершена до 1853 года; и великий тригонометрический обзор Индии, который в конечном итоге назвал и нанести на карту Маунт Эверест и другие гималайские вершины, было начато в 1801 году. Для французского государства наполеонов французская триангуляция была продлена Жан-Жозефом Транши в немецкую закон . завершен после 1815 года генерал -пруссом Карлом фон Мюфлинг . Между тем, математику Карлу Фридриху Гауссу было поручено с 1821 по 1825 год с триангуляцией Королевства Ганновера ( Гауссовая земля [ DE ] ), на котором он применил метод наименьших квадратов , чтобы найти наилучшее решение для проблем крупных систем. одновременных уравнений, приведенных более реальными измерениями, чем неизвестные.

Сегодня крупномасштабные триангуляционные сети для позиционирования в значительной степени были заменены глобальными навигационными спутниковыми системами, созданными с 1980-х годов, но многие из контрольных точек для более ранних опросов все еще выживают как ценные исторические особенности в ландшафте, такие как бетонные триангуляции. Установка для перестройки Великобритании (1936–1962), или точки триангуляции, установленные для геодезической арки Struve (1816–1855), теперь запланированный как сайт Всемирного наследия ЮНЕСКО .

Смотрите также

Англо-французское обследование (1784–1790)
Башня Билби
Великолепный тригонометрический обзор
Многолатерация , где точка рассчитывается с использованием повреждения по времени между другими известными точками
Параллакс
Резекция (ориентация)
Socet Set
Сферическая тригонометрия
Звездная триангуляция
Стереопсис
Точка Тригера

Ссылки

^ Jump up to: ^а ^{беременный} Дональд Рутледж Хилл (1984), История инженерии в классических и средневековых временах , Лондон: Croom Helm & La Salle, Иллинойс: открытый суд. ISBN 0-87548-422-0 . стр. 119-122
^ О'Коннор, Джон Дж.; Эдмунд , , Робертсон , Ф.
^ Майкл Джонс (2004), « Тихо Брахе, Картография и ландшафт в Скандинавии 16 -го века », в Ханнес Паланг (Эд), Европейские сельские ландшафты: упорство и изменения в глобализирующей среде, с.210
^ Мартин и Жан Норгат (2003), Сакстонс Хэмпшир: Обследование , Университет Портсмута

Дальнейшее чтение

Bagrow, L. (1964) История картографии ; Пересмотрен и расширен Рау Скелтоном. Гарвардский университет издательство.
Crone, GR (1978 [1953]) Карты и их создатели: введение в историю картографии (5 -е изд).
Tooley, RV & Bricker, C. (1969) История картографии: 2500 лет карт и карт -карт
Keay, J. (2000) Великая дуга: драматическая история о том, как Индия была нанесена на карту, и Эверест был назван . Лондон: Харпер Коллинз. ISBN 0-00-257062-9 .
Мердин, П. (2009) Полный Меридиан из славы: опасные приключения в соревнованиях, чтобы измерить Землю . Спрингер. ISBN 978-0-387-755533-5 .

[Hill-1] Jump up to: ^а ^{беременный} Дональд Рутледж Хилл (1984), История инженерии в классических и средневековых временах , Лондон: Croom Helm & La Salle, Иллинойс: открытый суд. ISBN 0-87548-422-0 . стр. 119-122

[MacTutor-2] О'Коннор, Джон Дж.; Эдмунд , , Робертсон , Ф.

[3] Майкл Джонс (2004), « Тихо Брахе, Картография и ландшафт в Скандинавии 16 -го века », в Ханнес Паланг (Эд), Европейские сельские ландшафты: упорство и изменения в глобализирующей среде, с.210

[4] Мартин и Жан Норгат (2003), Сакстонс Хэмпшир: Обследование , Университет Портсмута

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]