Танграм

Танграм состоящая ( китайский : 七巧板 ; пиньинь : qīqiƎobǎn ; букв. «семь досок навыков») — это головоломка, из семи плоских многоугольников, называемых тан , которые соединяются вместе, образуя фигуры. Цель состоит в том, чтобы воспроизвести узор (с только контуром), который обычно встречается в книге-головоломке, используя все семь частей без перекрытия. В качестве альтернативы загар можно использовать для создания оригинальных минималистичных дизайнов, которые ценятся либо за присущие им эстетические достоинства, либо в качестве основы для того, чтобы предложить другим повторить его контур. Считается, что он был изобретен в Китае где-то в конце 18 века, а затем вскоре после этого был перенесен в Америку и Европу торговыми судами. [1] На какое-то время он стал очень популярен в Европе, а затем снова во время Первой мировой войны . Это одна из наиболее широко известных головоломок в мире, которая использовалась для различных целей, включая развлечения, искусство и образование. [2] [3] [4]
Этимология
[ редактировать ]Происхождение английского слова «танграм» неясно. Согласно одной из гипотез, это соединение греческого элемента «-gram», производного от γράμμα («письменный знак, буква, то, что нарисовано»), при этом элемент «tan-», по различным предположениям, является китайским t'an «чтобы расширить» или кантонский t'ang «китайский». [5] Альтернативно, это слово может быть производным от архаичного английского «танграм», означающего «странная, замысловато придуманная вещь». [6]
В любом случае первое известное использование этого слова, как полагают, встречается в книге 1848 года «Геометрическая головоломка для молодежи» математика и будущего президента Гарвардского университета Томаса Хилла . [7] Хилл, вероятно, придумал этот термин в той же работе и активно продвигал это слово в многочисленных статьях, пропагандирующих использование головоломки в образовании, а в 1864 году это слово получило официальное признание в английском языке, когда оно было включено в Американский словарь Ноа Вебстера . [8]
История
[ редактировать ]Происхождение
[ редактировать ]Несмотря на его относительно недавнее появление на Западе, в Китае существует гораздо более древняя традиция развлечений с рассечением, которая, вероятно, сыграла роль в его вдохновении. В частности, модульные банкетные столы династии Сун имеют сверхъестественное сходство с игровыми элементами танграма, и существовали книги, посвященные тому, как складывать их вместе, образуя приятные узоры. [9]
Несколько китайских источников широко сообщают об известном эрудите из династии Сун Хуан Босы 黄伯思, который разработал форму развлечения для своих гостей на ужине, основанную на творческом расположении шести маленьких столиков, называемых 宴几 или 燕几 ( праздничные столы или столы с ласточками соответственно). На одной диаграмме они показаны в виде продолговатых прямоугольников, а в других отчетах предполагается, что седьмая таблица была добавлена позже, возможно, более поздним изобретателем.
Однако, согласно западным источникам, исторический китайский изобретатель танграма неизвестен, за исключением псевдонима Ян-чо-чу-ши (Тупой (?) Затворник, отшельник = 处士). Считается, что головоломка была первоначально представлена в книге под названием «Ци цзяо ту» , о которой уже сообщил Шань-цзяо в 1815 году как утерянная в его книге « Новые фигуры Танграма» . Тем не менее принято считать, что головоломка была изобретена примерно на 20 лет раньше. [10]
Выдающийся математик третьего века Лю Хуэй использовал в своих работах доказательства конструкции, и некоторые из них поразительно напоминают разработанные впоследствии банкетные столы, которые, в свою очередь, кажется, предвосхищают танграм. Хотя нет никаких оснований подозревать, что танграммы использовались в доказательстве теоремы Пифагора , как иногда сообщается, вполне вероятно, что этот стиль геометрических рассуждений продолжал оказывать влияние на китайскую культурную жизнь, что привело непосредственно к загадке. [11]
Первые годы попыток датировать Танграм были сбиты с толку популярной, но мошеннически написанной историей знаменитого создателя головоломок Сэмюэля Лойда в его «Восьмой книге Тан» 1908 года . Эта работа содержит множество причудливых особенностей, которые вызвали как интерес, так и подозрения среди современных ученых, пытавшихся проверить это сообщение. К 1910 году стало ясно, что это была мистификация. датированном этим годом, Оксфордского словаря В письме редактора сэра Джеймса Мюррея, от имени ряда китайских ученых известному головоломку Генри Дьюдени , говорится: «В результате было показано, что человек Тан, бог Тан и Книга Тана совершенно неизвестны китайской литературе, истории и традициям». [6] Несмотря на множество странных подробностей, дату создания Восьмой книги Тана для загадки 4000 лет древности пришлось рассматривать как совершенно необоснованную и ложную.
Достижение западного мира (1815–1820-е гг.)
[ редактировать ]
Самый ранний из сохранившихся танграмов был подарен филадельфийскому судоходному магнату и конгрессмену Фрэнсису Уолну в 1802 году, но только десять лет спустя западная аудитория в целом узнала об этой загадке. [1] вручили пару книг автора Сан-Ся-коя по этой теме (одну книгу с задачами и одну книгу с решениями) В 1815 году американскому капитану М. Доннальдсону, когда его корабль «Трейдер» пришвартовался туда, . Затем в феврале 1816 года их привезли на корабле в Филадельфию. Первая книга по танграму, опубликованная в Америке, была основана на паре, привезенной Доннальдсоном. [12]
В конце концов головоломка добралась до Англии, где стала очень модной. Увлечение быстро распространилось на другие европейские страны. В основном это произошло благодаря паре британских книг по танграму «Модная китайская головоломка » и прилагаемой книге решений « Ключ» . [13] Вскоре из Китая стали в большом количестве экспортироваться наборы танграм, изготовленные из различных материалов: от стекла до дерева и панциря черепахи. [14]
Многие из этих необычных и изысканных наборов танграма попали в Данию . Интерес Дании к танграмам резко возрос примерно в 1818 году, когда были опубликованы две книги по головоломке, вызвавшие большой энтузиазм. [15] Первым из них был «Мандаринен» («О китайской игре»). Это было написано студентом Копенгагенского университета и представляло собой научно-популярную работу об истории и популярности танграмов. Вторая, Det nye chinesiske Gaadespil (Новая китайская игра-головоломка), состояла из 339 головоломок, скопированных из «Восьмой книги Тана» , а также одной оригинальной. [15]
Одним из факторов, способствующих популярности игры в Европе, было то, что, хотя католическая церковь запрещала многие формы отдыха по субботам, она не возражала против игр-головоломок, таких как танграм. [16]
Второе увлечение в Германии (1891–1920-е гг.)
[ редактировать ]Танграмы были впервые представлены немецкой публике промышленником Фридрихом Адольфом Рихтером примерно в 1891 году. [17] Сервизы изготавливались из камня или ложной глины . [18] и продается под названием «Якорная головоломка». [17]
В международном масштабе Первая мировая война стала свидетелем значительного возрождения интереса к танграмам как в тылу, так и в окопах обеих сторон. В это время он иногда назывался «Сфинкс » (альтернативное название для наборов «Якорная головоломка»). [19] [20]
Парадоксы
[ редактировать ]
На рисунке 1 длины сторон обозначены в предположении, что стороны квадрата единичны.
На рисунке 2 наложение тел показывает, что безногое тело больше по площади ступни. Изменение площади часто остается незамеченным, поскольку √2 близко к 1,5.
танграма Парадокс — это ошибка расчленения: две фигуры составлены из одного и того же набора частей, одна из которых кажется подмножеством другой. [21] Одним из известных парадоксов является парадокс двух монахов , приписываемый Генри Дюдени , который состоит из двух одинаковых фигур, у одной из которых отсутствует ступня, а у другой. [22] В действительности на втором рисунке площадь стопы компенсируется чуть большим телом.
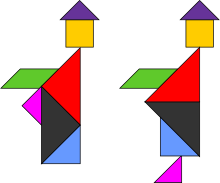
Парадокс двух монахов – две похожие фигуры, но у одной нет ступни:
Парадокс танграма Magic Dice Cup - из книги Сэма Лойда «Восьмая книга Тана» (1903). [23] Каждая из этих чашек была составлена из одних и тех же семи геометрических фигур. Но первая чашка целая, а остальные содержат пустоты разного размера. (Обратите внимание, что тот, что слева, немного короче двух других. Тот, что посередине, немного шире, чем тот, что справа, а тот, что слева, еще уже.) [24]

Парадокс обрезанного квадратного танграма - из книги Лойда «Восьмая книга Тана» (1903): [23]
Седьмая и восьмая фигуры представляют собой таинственный квадрат, построенный из семи частей: затем с отрезанным углом и все теми же семью частями. [25]
Количество конфигураций
[ редактировать ]
Только на основе текстов XIX века было создано более 6500 различных задач по танграму, и их число постоянно растет. [26] Фу Траинг Ван и Чуан-Чи Сюн доказали в 1942 г., что существует только тринадцать выпуклых конфигураций танграма (отрезки, проведенные между любыми двумя точками конфигурации, всегда полностью содержатся внутри конфигурации, т. е. конфигурации без углублений в контуре). [27] [28]
Куски
[ редактировать ]Выбрав единицу измерения так, чтобы семь частей можно было собрать в квадрат со стороной в одну единицу и площадью в одну квадратную единицу, получим следующие семь частей: [29]
- 2 больших прямоугольных треугольника (гипотенуза 1, стороны √ 2 / 2 , площадь 1 / 4 )
- 1 средний прямоугольный треугольник (гипотенуза √ 2 / 2 , стороны 1/2 площадь , 1 / 8 )
- 2 маленьких прямоугольных треугольника (гипотенуза 1/2 , стороны √ 2 / 4 , площадь 1 / 16 )
- 1 квадрат (стороны √ 2 / 4 , площадь 1 / 8 )
- 1 параллелограмм (стороны 1/2 и √ 2 / 4 , высота 1/4 площадь , 1 / 8 )
Из этих семи частей параллелограмм уникален тем, что у него нет симметрии отражения , а есть только вращательная симметрия , поэтому его зеркальное изображение можно получить, только перевернув его. Таким образом, это единственная деталь, которую, возможно, придется перевернуть при формировании определенных фигур.
См. также
[ редактировать ]- Танграм (видеоигра)
- Яйцо Колумба (головоломка танграм)
- Математическая головоломка
- Остомахион
- Плитка-головоломка
- Пикаграмма (3D-головоломка с магнитным танграмом)
- Блоки атрибутов
Ссылки
[ редактировать ]- ^ Jump up to: а б Слокам (2003) , с. 21.
- ^ Кампильо-Роблес, Хосе М.; Алонсо, Ибон; Гондра, Ане; Гондра, Нерея (1 сентября 2022 г.). «Расчет и измерение центра масс: универсальное занятие с использованием головоломок Танграма» . Американский журнал физики . 90 (9): 652. Бибкод : 2022AmJPh..90..652C . дои : 10.1119/5.0061884 . ISSN 0002-9505 . S2CID 251917733 .
- ^ Слокам (2001) , с. 9.
- ^ Форбраш, Уильям Байрон (1914). Руководство по игре . Джейкобс. п. 315 . Проверено 13 октября 2010 г.
- ^ Оксфордский словарь английского языка , 1910, св.
- ^ Jump up to: а б Слокам (2003) , с. 23.
- ^ Хилл, Томас (1848). Пазлы для обучения геометрии: в семнадцати карточках с номерами от первого до семнадцатого включительно . Бостон: Ум. Кросби и HP Николс.

- ^ Слокам (2003) , с. 25.
- ^ Слокам (2003) , с. 16.
- ^ Слокам (2003) , стр. 16–19.
- ^ Слокам (2003) , с. 15.
- ^ Слокам (2003) , с. 30.
- ^ Слокам (2003) , с. 31.
- ^ Слокам (2003) , с. 49.
- ^ Jump up to: а б Слокам (2003) , стр. 99–100.
- ^ Слокам (2003) , с. 51.
- ^ Jump up to: а б «Танграм — невероятная вневременная «китайская» головоломка» . www.archimedes-lab.org .
- ^ Решения Казначейства по таможенному и другим законам, Том 25 . Министерство финансов США. 1890–1926. п. 1421 . Проверено 16 сентября 2010 г.
- ^ Вятт (26 апреля 2006 г.). «Танграм – китайская головоломка» . h2g2 . Би-би-си. Архивировано из оригинала 2 октября 2011 г. Проверено 3 октября 2010 г.
- ^ Браман, Арлетт (2002). Дети всего мира играют! . Джон Уайли и сыновья. п. 10. ISBN 978-0-471-40984-7 . Проверено 5 сентября 2010 г.
- ^ Парадокс Танграма , Бариле, Маргарита, From MathWorld - веб-ресурс Wolfram, созданный Эриком В. Вайсштейном.
- ^ Дудени, Х. (1958). Забавы по математике . Нью-Йорк: Dover Publications.
- ^ Jump up to: а б «Восьмая книга Тана» Сэма Лойда . 1903 г. - через канал Танграм.
- ^ «Кубок волшебных кубиков» . 2 апреля 2011 г.
- ^ Лойд, Сэм (1968). Восьмая книга «Тан — 700 танграмм» Сэма Лойда с введением и решениями Питера Ван Нота . Нью-Йорк: Dover Publications. п. 25.
- ^ Слокам 2001 , с. 37.
- ^ Фу Трэнг Ван; Чуан-Чи Сюн (ноябрь 1942 г.). «Теорема о Танграме». Американский математический ежемесячник . 49 (9): 596–599. дои : 10.2307/2303340 . JSTOR 2303340 .
- ^ Прочтите, Рональд К. (1965). Танграмы: 330 головоломок . Нью-Йорк: Dover Publications. п. 53. ИСБН 0-486-21483-4 .
- ^ Брукс, Дэвид Дж. (1 декабря 2018 г.). «Как сделать классическую головоломку Танграм» . Журнал «Мальчишеская жизнь» . Проверено 10 марта 2020 г.
- Источники
- Слокам, Джерри (2001). Дао Танграма . Барнс и Ноубл. ISBN 978-1-4351-0156-2 .
- Слокам, Джерри (2003). Книга Танграм . Стерлинг. ISBN 978-1-4027-0413-0 .
Дальнейшее чтение
[ редактировать ]- Анно, Мицумаса. Математические игры Анно (три тома). Нью-Йорк: Philomel Books, 1987. ISBN 0-399-21151-9 (v. 1), ISBN 0-698-11672-0 (v. 2), ISBN 0-399-22274-X (v. 3).
- Ботерманс, Джек и др. Мир игр: их происхождение и история, как в них играть и как их создавать (перевод Wereld vol Spelletjes ). Нью-Йорк: факты в архиве, 1989. ISBN 0-8160-2184-8 .
- Дьюдени, HE. Забавы по математике . Нью-Йорк: Dover Publications, 1958.
- Гарднер, Мартин . «Математические игры - о фантастической истории и творческих задачах игры-головоломки Танграм», Scientific American , август 1974 г., стр. 98–103.
- Гарднер, Мартин. «Подробнее о танграмах», Scientific American, сентябрь 1974 г., стр. 187–191.
- Гарднер, Мартин. 2-я книга математических головоломок и развлечений Scientific American . Нью-Йорк: Саймон и Шустер, 1961. ISBN 0-671-24559-7 .
- Лойд, Сэм. Книга головоломок Танграма Сэма Лойда (Восьмая книга Тан, часть I) . Минеола, Нью-Йорк: Dover Publications, 1968.
- Слокам, Джерри и др. Загадки старые и новые: как их составить и решить . Де Меерн, Нидерланды: Plenary Publications International (Европа); Амстердам, Нидерланды: ADM International; Сиэтл: Распространено издательством Вашингтонского университета, 1986. ISBN 0-295-96350-6 .