Order-4 квадратная плитка соты

Order-4 квадратная плитка соты

Тип	Гиперболический регулярный сот Паракомпактная униформаная соты
Schläfli символы	{4,4,4} H {4,4,4} ↔ {4,4 ^1,1} {4 ^[4]}
Коксетерные диаграммы	↔ ↔ ↔ ↔ ↔ ↔ ↔ ↔ ↔
Ячейки	{4,4}
Лица	квадрат {4}
Крайя фигура	квадрат {4}
Вершина фигура	квадратная плитка , {4,4}
Двойной	Самостоятельно
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4] ${\overline {M}}_{3}$ , [4 ^1,1,1] ${\widehat {RR}}_{3}$ , [4 ^[4]]
Характеристики	Регулярные, квазирегулярные

В геометрии гиперболического 3-пространства является квадратная плитка order-4 квадратной плитки одним из 11 парадовальных регулярных сотов. Это паракомпакту , потому что он имеет бесконечные клетки и фигуры вершины , причем все вершины как идеальные точки в бесконечности. Данный Schläfli Symbol {4,4,4}, он имеет четыре квадратных пьеса по каждому краю и бесконечные квадратные петли вокруг каждой вершины на квадратной плюшевой вершине . ^{[ 1 ]}

Геометрический сот -это заполнение пространства многогранных или более высоких клеток , так что нет пробелов. Это пример более общей математической плитки или тесселяции в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как выпуклые равномерные соты . Они также могут быть сконструированы в неклидовах , таких как гиперболическая однородная соты . Любое конечное однородное политоп может быть проецирован на его оборудование , образуя равномерную сото в сферическом пространстве.

Симметрия

При соты на квадратную плитку заказа есть много конструкций с отражающей симметрией: Как обычный сот, ↔ с чередующимися типами (цветами) квадратных пьес и с 3 типами (цветами) квадратных пели в соотношении 2: 1: 1.

Еще две конструкции полумметрии с пирамидальными доменами имеют [4,4,1 ⁺, 4] Симметрия: ↔ , и ↔ .

Есть две высокоиндексные подгруппы, оба индекса 8: [4,4,4 ^*] ↔ [(4,4,4,4,1 ⁺)], с пирамидальным фундаментальным доменом: [((4, ∞, 4)), ((4, ∞, 4))] или ; и [4,4 ^*, 4], с 4 ортогональными наборами ультрапараллельных зеркал в октаэдрической фундаментальной области: .

Изображения

Квадратная плитка Horder-4-йлинг-соты аналогична 2D-гиперболическому апеирогональному плюеку , {∞, ∞}, с бесконечными апеирогональными гранями, и со всеми вершинами на идеальной поверхности.

Он содержит и Эта плитка 2- поверхности гиперциклов , которые похожи на эти паракопактные порядок-4 apeirogonal tilings :

Связанные политопы и соты

Квадратная плитка Hords-4 Pline Ciling Honey является обычным гиперболическим сотомком в 3-й пространстве. Это одна из одиннадцати обычных паракомпактных сотов.

11 Паракомпактные обычные соты
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

есть девять однородных сотов В семье коксеров Group , включая эту обычную форму.

[4,4,4] Семейные соты
{4,4,4}	r{4,4,4}	t{4,4,4}	rr{4,4,4}	t_0,3{4,4,4}	2t{4,4,4}	tr{4,4,4}	t_0,1,3{4,4,4}	t_0,1,2,3{4,4,4}

Это часть последовательности сотовье с квадратной вершиной.

{p, 4,4} Соты v Т и
Space	E³	H³
Form	Affine	Paracompact		Noncompact
Name	{2,4,4}	{3,4,4}	{4,4,4}	{5,4,4}	{6,4,4}	..{∞,4,4}
Coxeter
Image
Cells	{2,4}	{3,4}	{4,4}	{5,4}	{6,4}	{∞,4}

Это часть последовательности сотов с квадратными плиточными клетками:

{4,4, P} Соты v Т и
Space	E³	H³
Form	Affine	Paracompact		Noncompact
Name	{4,4,2}	{4,4,3}	{4,4,4}	{4,4,5}	{4,4,6}	...{4,4,∞}
Coxeter
Image
Vertex figure	{4,2}	{4,3}	{4,4}	{4,5}	{4,6}	{4,∞}

Это часть последовательности квазирегулярной полихоры и сотов:

Квазирегулярная полихора и соты: h {4, p, q}
Space	Finite	Affine	Compact	Paracompact
Schläfli symbol	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
Schläfli symbol	$\left\{3,{3 \atop 3}\right\}$	$\left\{3,{4 \atop 3}\right\}$	$\left\{3,{5 \atop 3}\right\}$	$\left\{3,{6 \atop 3}\right\}$	$\left\{4,{4 \atop 3}\right\}$	$\left\{4,{4 \atop 4}\right\}$
Coxeter diagram	↔	↔	↔	↔	↔	↔
Coxeter diagram	↔					↔
Image
Vertex figure r{p,3}

Исправленная order-4 квадратная плитка соты

Исправленная order-4 квадратная плитка соты
Тип	Паракомпактная униформаная соты
Schläfli символы	r {4,4,4} или t ₁ {4,4,4}
Коксетерные диаграммы	↔
Ячейки	{4,4} r {4,4}
Лица	квадрат {4}
Вершина фигура	куб
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4] ${\overline {M}}_{3}$ , [4 ^1,1,1]
Характеристики	Квазирегулярные или регулярные, в зависимости от симметрии

Исправленное расположение-4 шестиугольное соты для плитки , t ₁ {4,4,4}, Имеет квадратные плиточные грани, с кубической вершиной . Это то же самое, что и обычная квадратная плитка соты , {4,4,3}, .

Усеченные заказа-4 квадратные плитки соты

Усеченные заказа-4 квадратные плитки соты
Тип	Паракомпактная униформаная соты
Schläfli символы	t {4,4,4} или t _0,1 {4,4,4}
Коксетерные диаграммы	↔ ↔ ↔
Ячейки	{4,4} t {4,4}
Лица	квадрат {4} Octagon {8}
Вершина фигура	квадратная пирамида
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4] ${\overline {M}}_{3}$ , [4 ^1,1,1]
Характеристики	Вершино-транзитный

Усеченная квадратная плитка соты , t _0,1 {4,4,4}, Имеет квадратную плитку и усеченную квадратную плиточную грани, с квадратной пирамидой вершиной фигуры .

Bitruncated Order-4 квадратная плитка соты

Bitruncated Order-4 квадратная плитка соты
Тип	Паракомпактная униформаная соты
Schläfli символы	2t {4,4,4} или T _1,2 {4,4,4}
Коксетерные диаграммы	↔ ↔ ↔
Ячейки	t {4,4}
Лица	квадрат {4} Octagon {8}
Вершина фигура	тетрагональный дефеноид
Коксетерские группы	$2\times {\overline {N}}_{3}$ , [[4,4,4]] ${\overline {M}}_{3}$ , [4 ^1,1,1] ${\widehat {RR}}_{3}$ , [4 ^[4]]
Характеристики	Вертно-транспортный, транс-транспортный, клеточный транспортный

Bitruncated Order-4 квадратная плитка Honeycomb , t _1,2 {4,4,4}, имеет усеченные квадратные плиточные аспекты, с тетрагональной дефеноидной вершиной .

Кантел-заказа-4 квадратные плитки соты

Кантел-заказа-4 квадратные плитки соты
Тип	Паракомпактная униформаная соты
Schläfli символы	RR {4,4,4} или T _0,2 {4,4,4}
Коксетерные диаграммы
Ячейки	{} x {4} r {4,4} RR {4,4}
Лица	квадрат {4}
Вершина фигура	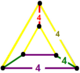Треугольная призма
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4] ${\overline {R}}_{3}$ , [3,4,4]
Характеристики	Vertex-транзитный, трансферат с краями

Кантеллененный rond-4 квадратный плиток соты , то же самое, что упряхленная квадратная плитка соты , Полем Он имеет кубические и квадратные аспекты с треугольной фигурой вершины.

Кантитринг-4 квадратные плитки соты

Кантитринг-4 квадратные плитки соты
Тип	Паракомпактная униформаная соты
Schläfli символы	tr {4,4,4} или t _0,1,2 {4,4,4}
Коксетерные диаграммы	↔
Ячейки	{} x {4} tr {4,4} t {4,4}
Лица	квадрат {4} Octagon {8}
Вершина фигура	зеркальный сфиноид
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4] ${\overline {R}}_{3}$ , [3,4,4] ${\overline {M}}_{3}$ , [4 ^1,1,1]
Характеристики	Вершино-транзитный

Кантитрированная лента-4 квадратная плитка соты , такой же, как у усеченной квадратной плитки соты , Полем Он содержит куб и усеченные квадратные плиточные грани, с зеркальным сфиноидным вершинной фигурой.

Это то же самое, что усеченная квадратная плитка соты , .

Runcinated Order-4 квадратная плитка соты

Runcinated Order-4 квадратная плитка соты
Тип	Паракомпактная униформаная соты
Schläfli символы	T _0,3 {4,4,4}
Коксетерные диаграммы	↔ ↔
Ячейки	{4,4} {} x {4}
Лица	квадрат {4}
Вершина фигура	квадратный антипризм
Коксетерские группы	$2\times {\overline {N}}_{3}$ , [[4,4,4]]
Характеристики	Vertex-транзитный, трансферат с краями

Runcinated Order-4 квадратная плитка соты , t _0,3 {4,4,4}, имеет квадратную плитку и кубические грани, с антипризма квадратной вершиной .

Runcitruncated order-4 квадратная плитка соты

Runcitruncated order-4 квадратная плитка соты
Тип	Паракомпактная униформаная соты
Schläfli символы	T _0,1,3 {4,4,4}
Коксетерные диаграммы	↔
Ячейки	t {4,4} RR {4,4} {} x {4} {8} x {}
Лица	квадрат {4} Octagon {8}
Вершина фигура	квадратная пирамида
Коксетерские группы	${\overline {N}}_{3}$ , [4,4,4]
Характеристики	Вершино-транзитный

Runcitruncated order-4 квадратная плитка соты , t _0,1,3 {4,4,4}, имеет квадратную плитку , усеченную квадратную плитку , кубик и восьмиугольные аспекты призмы, с квадратной пирамидой .

Квадратная плитка runcicantellated order-4 квадратной плитки эквивалентна обезжиренной квадратной плитке.

Вс еще неотрасчитый порядок-4 квадратные плитки соты

Вс еще неотрасчитый порядок-4 квадратные плитки соты
Тип	Паракомпактная униформаная соты
Schläfli символы	T _0,1,2,3 {4,4,4}
Коксетерные диаграммы
Ячейки	tr {4,4} {8} x {}
Лица	квадрат {4} Octagon {8}
Вершина фигура	Дигональный Дисфеноид
Коксетерские группы	$2\times {\overline {N}}_{3}$ , [[4,4,4]]
Характеристики	Вершино-транзитный

Оснавочный порядок-4 квадратный плиток соты , t _0,1,2,3 {4,4,4}, имеет усеченную квадратную плитку и восьмиугольные аспекты призмы , с дигональной дипосфеноидной вершиной фигурой .

Чередовый заказ-4 квадратный плиток соты

Чередованная квадратная плитка соты -это конструкция нижней симметрии квадратной плитки.

Кантский заказ-4 квадратные плитки соты

Квадратная плитка кантри-4 квадратной плитки -это конструкция нижней симметрии усеченного квадратного соты на 4 квадратного заказа .

Runcic order-4 квадратная плитка соты

Квадратная плитка runcic order-4 квадратной плитки представляет собой конструкцию нижней симметрии квадратной плитки order-3 .

Runcicantic order-4 квадратная плитка соты

Ругсикантский квадратный плиточный соты -это конструкция с нижней симметрией квадратной плитки .

Квадратный заказ-4 квадратные плитки соты

Квадратный заказ-4 квадратные плитки соты
Тип	Паракомпактная униформаная соты
Schläfli символы	Q {4,4,4}
Коксетерные диаграммы
Ячейки	t {4,4} {4,4}
Лица	квадрат {4} Octagon {8}
Вершина фигура	квадратный антипризм
Коксетерские группы	${\widehat {RR}}_{3}$ , [4 ^[4]]
Характеристики	Vertex-транзитный, трансферат с краями

Квадратный Quarter Order-4 квадратный соты , Q {4,4,4}, , или , имеет усеченную квадратную плитку и квадратную плиточную аспекты, с квадратной антипризмом .

Смотрите также

Ссылки

^ Коксетер Красота геометрии , 1999, глава 10, Таблица III

Коксетер , обычные политопы , 3 -й. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: обычные политопы и соты, с. 294–296)
Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Регулярные соты в гиперболическом пространстве ) Таблица III
Джеффри Р. недели форма пространства, 2 -е издание ISBN 0-8247-0709-5 (Глава 16-17: Геометрия на трех органах I, II)
Норман Джонсон унифицированные политопы , рукопись
- NW Johnson : Теория единообразных политопов и сотов , доктор философии. Диссертация, Университет Торонто, 1966
- NW Johnson: Геометрия и преобразования , (2018) Глава 13:
- Норман В. Джонсон и Азия Ивик Вайс квадратичные целые числа и коксетерные группы PDF Can. J. Math. Тол. 51 (6), 1999 с. 1307–1336

[1] Коксетер Красота геометрии , 1999, глава 10, Таблица III

[ 1 ]