Ведьма из Аньези

По математике ведьма Аньези ( Итальянское произношение: [aɲˈɲeːzi, -eːsi; -ɛːzi] ) — кубическая плоская кривая, определяемая двумя диаметрально противоположными точками окружности.

Кривая была изучена еще в 1653 году Пьером Ферма , в 1703 году Гвидо Гранди и Исааком Ньютоном . Он получил свое название от итальянского математика Марии Гаэтаны Аньези, опубликовавшей его в 1748 году. Итальянское название la versiera di Agnesi основано на латинском versoria ( лист парусных кораблей) и синусоиде против . Это было прочитано Джоном Колсоном как l'avversiera di Agnesi , где avversiera переводится как «женщина, которая против Бога» и интерпретируется как «ведьма». ^[1]^[2]^[3]^[4]

График представляет собой производной функции арктангенса пример ведьмы Аньези. Как функция плотности вероятности распределения Коши , ведьма Аньези имеет применение в теории вероятностей . Это также приводит к явлению Рунге при приближении функций полиномами спектральных , используется для аппроксимации распределения энергии линий и моделирования формы холмов.

Ведьма касается своей определяющей окружности в одной из двух определяющих точек и асимптотична касательной к окружности в другой точке. Он имеет уникальную вершину (точку крайней кривизны) в точке касания с определяющей окружностью, которая также является соприкасающейся окружностью в этой точке. Он также имеет две конечные точки перегиба и одну бесконечную точку перегиба. Площадь между ведьмой и ее асимптотической линией в четыре раза превышает площадь определяющего круга, а объем вращения кривой вокруг ее определяющей линии в два раза превышает объем тора вращения ее определяющего круга.

Строительство

Анимация, показывающая постройку ведьмы Аньези.

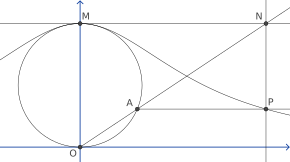
Чтобы построить эту кривую, начните с любых двух точек O и M и нарисуйте круг с OM диаметром . Для любой другой точки A на окружности пусть N будет точкой пересечения секущей линии OA и касательной в M. точке Пусть P — точка пересечения линии, перпендикулярной OM, проходящей через A , и линии, параллельной , проходящей через N. OM Тогда П лежит на ведьме Аньези. Ведьма состоит из всех точек P которые можно построить таким образом из одного и того же выбора O и M. , ^[5] В качестве предельного случая он включает в себя точку М. саму

Уравнения

Предположим, что точка О находится в начале координат , а точка М лежит на положительной $y$ -ось, и что круг диаметром OM имеет радиус $a$ . Тогда ведьма, построенная из O и M, имеет декартово уравнение ^[6]^[7] $y={\frac {8a^{3}}{x^{2}+4a^{2}}}.$ Это уравнение можно упростить, выбрав $a={\tfrac {1}{2}}$ , к форме $y={\frac {1}{x^{2}+1}}.$ или, что то же самое, очистив знаменатели , как кубическое алгебраическое уравнение $(x^{2}+1)y=1.$ В упрощенном виде эта кривая график производной собой арктангенса представляет . ^[8]

Ведьму Аньези также можно описать параметрическими уравнениями , параметром которых $θ$ является угол между OM и OA , измеренный по часовой стрелке: ^[6]^[7] ${\begin{aligned}x&=2a\tan \theta ,\\y&=2a\cos ^{2}\theta .\end{aligned}}$

Характеристики

Основные свойства этой кривой можно вывести из интегрального исчисления .Площадь между ведьмой и ее асимптотической линией в четыре раза превышает площадь фиксированного круга. $4\pi a^{2}$ . ^[6]^[7]^[9]Объем обращения ведьмы Аньези вокруг ее асимптоты равен $4\pi ^{2}a^{3}$ . ^[6] Это в два раза больше объема тора, образованного вращением определяющего круга ведьмы вокруг той же линии. ^[9]

Кривая имеет уникальную вершину в точке касания с определяющей ее окружностью. То есть эта точка является единственной точкой, где кривизна достигает локального минимума или локального максимума. ^[10] Определяющим кругом ведьмы является также ее соприкасающийся круг в вершине. ^[11] уникальный круг, который «целует» кривую в этой точке, имея одинаковую ориентацию и кривизну. ^[12] Поскольку это соприкасающийся круг в вершине кривой, он имеет третьего порядка . контакт с кривой ^[13]

Кривая имеет две точки перегиба , в точках $\left(\pm {\frac {2a}{\sqrt {3}}},{\frac {3a}{2}}\right)$ соответствующие углам $\theta =\pm \pi /6$ . ^[6]^[7] Если рассматривать кривую на проективной плоскости, то существует также третья бесконечная точка перегиба, в точке, где линия на бесконечности пересекается асимптотической линией. Поскольку одна из ее точек перегиба бесконечна, у ведьмы есть минимально возможное количество конечных действительных точек перегиба любой неособой кубической кривой. ^[14]

Наибольшая площадь прямоугольника , которую можно вписать между ведьмой и ее асимптотой, равна $4a^{2}$ , для прямоугольника, высота которого равна радиусу определяющего круга, а ширина в два раза больше диаметра круга . ^[9]

История

Ранние исследования

Кривая была изучена Пьером де Ферма в его трактате о квадратуре 1659 года . В ней Ферма вычисляет площадь под кривой и (без подробностей) утверждает, что тот же метод распространяется и на циссоиду Диокла . Ферма пишет, что эта кривая была подсказана ему « ab erudito geometra » [ученым геометром]. ^[16] Паради, Пла и Виадер (2008) предполагают, что геометром, который предложил Ферма эту кривую, мог быть Антуан де Лалубер . ^[17]

Приведенную выше конструкцию этой кривой нашел Гранди (1718) ; такая же конструкция была найдена и ранее Исааком Ньютоном , но опубликована лишь посмертно позже, в 1779 году. ^[18]Гранди (1718) название versiera (на итальянском языке) или versoria (на латыни). также предложил для кривой ^[19] Латинский термин также используется для обозначения листа , веревки, которая вращает парус, но вместо этого Гранди, возможно, имел в виду просто ссылку на функцию стиха , которая проявилась в его конструкции. ^[9]^[18]^[20]^[21]

В 1748 году Мария Гаэтана Аньези опубликовала «Аналитические учреждения для использования итальянской молодежью» — ранний учебник по математическому анализу . ^[15] В него, предварительно рассмотрев две другие кривые, она включает исследование этой кривой. Она определяет кривую геометрически как геометрическое место точек, удовлетворяющих определенной пропорции, определяет ее алгебраическое уравнение, находит ее вершину, асимптотическую линию и точки перегиба. ^[22]

Этимология

Мария Гаэтана Аньези назвала кривую по Гранди, versiera . ^[20]^[22] было принято говорить По совпадению, в то время в Италии о Дьяволе другими словами, такими как aversiero или versiero , происходящими от латинского adversarius , «противник» Бога. Версьера , в частности, использовалась для обозначения жены дьявола или «ведьмы». ^[23] Из-за этого профессор Кембриджа Джон Колсон неправильно перевел название кривой как «ведьма». ^[24] Различные современные работы об Аньези и о кривой предполагают несколько разные догадки, как именно произошел этот неправильный перевод. ^[25]^[26] Стройк упоминает, что: ^[22]

Слово [ versiera ] происходит от латинского vertere — поворачивать, но также является аббревиатурой итальянского avversiera — женщины-дьявола. Некоторые остроумцы в Англии однажды перевели это слово как «ведьма», и этот глупый каламбур до сих пор бережно сохраняется в большинстве наших учебников на английском языке. ... Кривая уже появлялась в трудах Ферма ( Oeuvres , I, 279–280; III, 233–234) и других; название versiera происходит от Гвидо Гранди ( Quadratura circuli et Hyperbolae , Пиза, 1703). Кривая относится к типу 63 по классификации Ньютона . ... Первым, кто использовал термин «ведьма» в этом смысле, возможно, был Б. Уильямсон, Интегральное исчисление , 7 (1875), 173; ^[27] см . Оксфордский словарь английского языка .

С другой стороны, Стивен Стиглер предполагает, что сам Гранди «возможно, играл словами», двойной каламбур, связывающий дьявола со стихом и функцию синуса с формой женской груди (оба из которых можно записать как «сено» по-итальянски). ^[18]

Приложения

Масштабированная версия кривой представляет собой функцию плотности вероятности распределения Коши . Это распределение вероятностей случайной величины $x$ определяется следующим случайным экспериментом : для фиксированной точки $p$ над $x$ -оси, выберите равномерно и случайным образом линию, проходящую через $p$ , и пусть $x$ быть координатой точки, где эта случайная линия пересекает ось. Распределение Коши имеет пиковое распределение, визуально напоминающее нормальное распределение , но его тяжелые хвосты не позволяют ему иметь ожидаемое значение по обычным определениям, несмотря на его симметрию. С точки зрения самой ведьмы это означает, что $x$ -координата центроида . области между кривой и ее асимптотической линией не определена четко, несмотря на симметрию этой области и конечную площадь ^[18]^[28]

В численном анализе при аппроксимации функций с использованием полиномиальной интерполяции с равноотстоящими друг от друга точками интерполяции для некоторых функций может случиться так, что использование большего количества точек создает худшие аппроксимации, так что интерполяция расходится от функции, которую она пытается аппроксимировать, а не сходится к ней. . Это парадоксальное поведение называется феноменом Рунге . Впервые он был обнаружен Карлом Дэвидом Толме Рунге для функции Рунге. $y=1/(1+25x^{2})$ , еще одна масштабированная версия ведьмы Аньези, при интерполяции этой функции на интервале $[-1,1]$ . То же самое происходит и с ведьмой. $y=1/(1+x^{2})$ себя в более широком интервале $[-5,5]$ . ^[29]

Ведьма Аньези аппроксимирует спектральное распределение энергии спектральных линий , особенно рентгеновских линий. ^[30]

Поперечное сечение гладкого холма имеет форму, похожую на Ведьмину. ^[31] Кривые такой формы использовались в качестве типичного топографического препятствия в потоке при математическом моделировании. ^[32]^[33] одиночные волны на глубокой воде. Такую форму могут принимать и ^[34]^[35]

Версия этой кривой была использована Готфридом Вильгельмом Лейбницем для вывода формулы Лейбница для $π$ . Эта формула, бесконечный ряд ${\frac {\pi }{4}}=1\,-\,{\frac {1}{3}}\,+\,{\frac {1}{5}}\,-\,{\frac {1}{7}}\,+\,{\frac {1}{9}}\,-\,\cdots ,$ можно получить, приравнивая площадь под кривой к интегралу от функции $1/(1+x^{2})$ , используя в ряд Тейлора разложение этой функции как бесконечную геометрическую прогрессию $1-x^{2}+x^{4}-x^{6}+\cdots$ и интегрируем почленно. ^[7]

В популярной культуре

«Ведьма из Аньези» — название романа Роберта Спиллера. Он включает в себя сцену, в которой учитель излагает версию истории этого термина. ^[36]

Ведьма Аньези — это также название музыкального альбома джазового квартета Radius. На обложке альбома изображено построение ведьмы. ^[37]

Ссылки

^ Wolfram MathWorld, Ведьма Аньези
^ Линн М. Осен: Женщины в математике. MIT Press, Кембридж, Массачусетс, 1975, ISBN 0-262-15014-X, S. 45.
^ Саймон Сингх : Загадка Ферма. Стремление решить величайшую математическую задачу в мире. Walker Books, Нью-Йорк, 1997, ISBN 0-471-27047-4, S. 100.
^ Дэвид Дж. Дарлинг: Универсальная книга по математике. От абракадабры до парадоксов Зенона. Wiley International, Хобокен, штат Нью-Джерси, 2004 г., ISBN 0-8027-1331-9, стр. 8.
^ Иглз, Томас Генри (1885), «Ведьма Аньези» , Конструктивная геометрия плоских кривых: с многочисленными примерами , Macmillan and Company, стр. 313–314.
^ Jump up to: ^а ^б ^с ^д ^и Лоуренс, Дж. Деннис (2013), «4.3 Ведьма Аньези (Ферма, 1666; Аньези, 1748)» , Каталог специальных плоских кривых , Dover Books on Mathematics, Courier Corporation, стр. 90–93, ISBN 9780486167664
^ Jump up to: ^а ^б ^с ^д ^и Йейтс, Роберт К. (1954), «Ведьма Аньези», Кривые и их свойства (PDF) , Классика математического образования, том. 4, Национальный совет учителей математики, стр. 237–238.
^ Коэн, Дэвид В.; Хенле, Джеймс М. (2005), Исчисление: язык изменений , Jones & Bartlett Learning, с. 351, ISBN 9780763729479
^ Jump up to: ^а ^б ^с ^д Ларсен, Гарольд Д. (январь 1946 г.), «Ведьма Аньези», School Science and Mathematics , 46 (1): 57–62, doi : 10.1111/j.1949-8594.1946.tb04418.x
^ Гибсон, К.Г. (2001), Элементарная геометрия дифференцируемых кривых: введение для студентов , Кембридж: Издательство Кембриджского университета, упражнение 9.1.9, стр. 131 , номер домена : 10.1017/CBO9781139173377 , ISBN 0-521-80453-1 , МР 1855907
^ Хафтендорн, Дёрте (2017), «4.1 Versiera, кривая ведьмы», Исследование и понимание кривых (на немецком языке), Springer, стр. 79–91, doi : 10.1007/978-3-658-14749-5 , ISBN 978-3-658-14748-8 . О соприкасающемся круге см., в частности, с. 81: «Производящий круг — это круг кривизны широкой Версиеры в ее вершине».
^ Липсман, Рональд Л.; Розенберг, Джонатан М. (2017), Многомерное исчисление с MATLAB®: с приложениями к геометрии и физике , Springer, стр. 42, ISBN 9783319650708 Круг «целует» кривую с точностью до второго порядка, поэтому получил название соприкасающегося круга (от латинского слова «поцелуй»).
^ Фукс, Дмитрий ; Табачников, Серж (2007), Математический омнибус: тридцать лекций по классической математике , Провиденс, Род-Айленд: Американское математическое общество, с. 142, номер домена : 10.1090/mbk/046 , ISBN 978-0-8218-4316-1 , МР 2350979
^ Арнольд, VI (2005), «Принцип топологической экономии в алгебраической геометрии», Обзоры по современной математике , Серия лекций Лондонского математического общества, том. 321, Кембридж: Издательство Кембриджского университета, стр. 13–23, doi : 10.1017/CBO9780511614156.003 , MR 2166922 . См., в частности, стр. 15–16 .
^ Jump up to: ^а ^б Аньези, Мария Гаэтана (1748 г.), Аналитические учреждения для использования итальянской молодежи. См., в частности, задачу 3, стр. 380–382 и рис. 135 .
^ де Ферма, Пьер (1891), Oevres (на латыни), vol. 1, Готье-Вилларс и др., стр. 280–285
^ Рай, Джеймс; Пла, Джозеф; Виадер, Пелегри (2008), «Метод квадратур Ферма» , Revue d'Histoire des Mathématiques , 14 (1): 5–51, MR 2493381
^ Jump up to: ^а ^б ^с ^д Стиглер, Стивен М. (август 1974 г.), «Исследования по истории вероятности и статистики. XXXIII. Коши и ведьма Аньези: историческая заметка о распределении Коши», Biometrika , 61 (2): 375–380, doi : 10.1093/biomet/61.2.375 , JSTOR 2334368 , MR 0370838
↑ В своих примечаниях к «Трактату о естественно ускоренном движении» Галилея Гранди ссылался на «ту кривую, которую я описываю в своей книге квадратур [1703], в положении IV, рожденную из стихов, которую я обычно называю Versiera , но на латыни Версория ». См. Галилей, Опера , 3: 393. Новый термин можно найти у Лоренцо Лоренцини, Exercitatio Geometraa , xxxi: «сидеть pro exemplo curva illa, quam Doctissimus magnusque geometra Guido Grandus Versoria nominat».
^ Jump up to: ^а ^б Трусделл, К. (1991), «Исправление и дополнения к «Марии Гаэтане Аньези» », Архив истории точных наук , 43 (4): 385–386, doi : 10.1007/BF00374764 , […] nata da' seni versi , который в моей стране обычно называется Версиера на латыни, но Версория […]
^ Гранди, Дж. (1718), «Примечания к трактату Галилея об ускоренном естественном движении», Opera Di Galileo Galilei (на итальянском языке), том. III, Флоренция, с. 393 . Цитируется Стиглером (1974) .
^ Jump up to: ^а ^б ^с Перевод работы Аньези об этой кривой можно найти в: Струик, Дирк Дж. (1969), Справочник по математике, 1200–1800 , Кембридж, Массачусетс: Издательство Гарвардского университета, стр. 178–180.
^ Пьетро Фанфани , Тосканский словарь , с. 334
^ Малкроне, Т.Ф. (1957), «Названия кривой Аньези», American Mathematical Monthly , 64 (5): 359–361, doi : 10.2307/2309605 , JSTOR 2309605 , MR 0085163
^ Сингх, Саймон (1997), Загадка Ферма: эпический поиск решения величайшей в мире математической проблемы , Нью-Йорк: Уокер и компания, стр. 100 , ISBN 0-8027-1331-9 , МР 1491363
^ Дарлинг, Дэвид (2004), Универсальная книга по математике: от абракадабры до парадоксов Зенона , Хобокен, Нью-Джерси: John Wiley & Sons, стр. 8, ISBN 0-471-27047-4 , МР 2078978
^ Оксфордский словарь английского языка , Oxford University Press, 2018, witch, n .2, 4(e) , получено 3 июля 2018 г. , 1875 г. Б. Уильямсон Элем. Обращаться. Интегральное исчисление vii. 173 Найдите область между ведьмой Аньези. $xy^{2}=4a^{2}(2a-x)$ и ее асимптота.
^ Александр, Дж. Маккензи (2012), «Теория принятия решений встречает ведьму Аньези», Journal of Philosophy , 109 (12): 712–727, doi : 10.5840/jphil20121091233
^ Купильяри, Антонелла ; ДеТомас, Элизабет (весна 2007 г.), «Разоблачение колдовского поведения функции Рунге», Mathematics and Computer Education , 41 (2): 143–156, ПроКвест 235858817
^ Спенсер, Рой К. (сентябрь 1940 г.), «Свойства ведьмы Аньези - применение к подбору формы спектральных линий», Журнал Оптического общества Америки , 30 (9): 415, Бибкод : 1940JOSA ... 30 ..415S , дои : 10.1364/josa.30.000415
^ Коппин, Пенсильвания; Брэдли, EF; Финниган, Дж. Дж. (апрель 1994 г.), «Измерения потока над удлиненным хребтом и зависимость его термостабильности: среднее поле», Boundary-Layer Meteorology , 69 (1–2): 173–199, Bibcode : 1994BoLMe..69. .173C , doi : 10.1007/bf00713302 S2CID 119956741. Полезной , общей формой для формы холма является так называемый профиль «Ведьмы Аньези».
^ Снайдер, Уильям Х.; Томпсон, Роджер С.; Эскридж, Роберт Э.; Лоусон, Роберт Э.; Кастро, Ян П.; Ли, Джей Ти; Хант, Джулиан CR; Огава, Ясуши (март 1985 г.), «Структура сильно стратифицированного потока над холмами: концепция разделительной линии тока», Journal of Fluid Mechanics , 152 (–1): 249, Бибкод : 1985JFM...152..249S , doi : 10.1017/s0022112085000684 , S2CID 123563729
^ Лэмб, Кевин Г. (февраль 1994 г.), «Численное моделирование стратифицированного невязкого течения над гладким препятствием» (PDF) , Journal of Fluid Mechanics , 260 (–1): 1, Bibcode : 1994JFM...260.... 1L , doi : 10.1017/s0022112094003411 , S2CID 49355530 , заархивировано из оригинала (PDF) 6 января 2014 г.
^ Бенджамин, Т. Брук (сентябрь 1967 г.), «Внутренние волны постоянной формы в жидкостях на большой глубине», Journal of Fluid Mechanics , 29 (3): 559, Bibcode : 1967JFM....29..559B , doi : 10.1017 /s002211206700103x , S2CID 123065419
^ Нунан, Джули А.; Смит, Роджер К. (сентябрь 1985 г.), «Линейные и слабонелинейные теории внутренних волн в применении к волнам« ипомеи »», Geophysical & Astrophysical Fluid Dynamics , 33 (1–4): 123–143, Бибкод : 1985GApFD..33 ..123N , дои : 10.1080/03091928508245426
^ Филлипс, Дэйв (12 сентября 2006 г.), «Местный учитель, автор формулирует математику в книгах» , The Gazette.
^ Radius – Witch Of Agnesi (Plutonium Records, 2002) , Discogs , получено 28 мая 2018 г.

Внешние ссылки

«Ведьма Аньези» в Индексе знаменитых кривых MacTutor
Вайсштейн, Эрик В. , «Ведьма Аньези» , MathWorld
«Ведьма Аньези» Криса Баучера на основе работы Эрика В. Вайсстейна « Демонстрационный проект Вольфрама» .
«Ведьма Аньези» на «mathcurve»
Лэмб, Эвелин (28 мая 2018 г.), «Несколько моих любимых мест: Ведьма Аньези» , «Корни единства » , Scientific American

[1] Wolfram MathWorld, Ведьма Аньези

[2] Линн М. Осен: Женщины в математике. MIT Press, Кембридж, Массачусетс, 1975, ISBN 0-262-15014-X, S. 45.

[3] Саймон Сингх : Загадка Ферма. Стремление решить величайшую математическую задачу в мире. Walker Books, Нью-Йорк, 1997, ISBN 0-471-27047-4, S. 100.

[4] Дэвид Дж. Дарлинг: Универсальная книга по математике. От абракадабры до парадоксов Зенона. Wiley International, Хобокен, штат Нью-Джерси, 2004 г., ISBN 0-8027-1331-9, стр. 8.

[eagles-5] Иглз, Томас Генри (1885), «Ведьма Аньези» , Конструктивная геометрия плоских кривых: с многочисленными примерами , Macmillan and Company, стр. 313–314.

[lawrence-6] Jump up to: ^а ^б ^с ^д ^и Лоуренс, Дж. Деннис (2013), «4.3 Ведьма Аньези (Ферма, 1666; Аньези, 1748)» , Каталог специальных плоских кривых , Dover Books on Mathematics, Courier Corporation, стр. 90–93, ISBN 9780486167664

[yates-7] Jump up to: ^а ^б ^с ^д ^и Йейтс, Роберт К. (1954), «Ведьма Аньези», Кривые и их свойства (PDF) , Классика математического образования, том. 4, Национальный совет учителей математики, стр. 237–238.

[calc-8] Коэн, Дэвид В.; Хенле, Джеймс М. (2005), Исчисление: язык изменений , Jones & Bartlett Learning, с. 351, ISBN 9780763729479

[larsen-9] Jump up to: ^а ^б ^с ^д Ларсен, Гарольд Д. (январь 1946 г.), «Ведьма Аньези», School Science and Mathematics , 46 (1): 57–62, doi : 10.1111/j.1949-8594.1946.tb04418.x

[egdc-10] Гибсон, К.Г. (2001), Элементарная геометрия дифференцируемых кривых: введение для студентов , Кембридж: Издательство Кембриджского университета, упражнение 9.1.9, стр. 131 , номер домена : 10.1017/CBO9781139173377 , ISBN 0-521-80453-1 , МР 1855907

[haftendorn-11] Хафтендорн, Дёрте (2017), «4.1 Versiera, кривая ведьмы», Исследование и понимание кривых (на немецком языке), Springer, стр. 79–91, doi : 10.1007/978-3-658-14749-5 , ISBN 978-3-658-14748-8 . О соприкасающемся круге см., в частности, с. 81: «Производящий круг — это круг кривизны широкой Версиеры в ее вершине».

[kiss-12] Липсман, Рональд Л.; Розенберг, Джонатан М. (2017), Многомерное исчисление с MATLAB®: с приложениями к геометрии и физике , Springer, стр. 42, ISBN 9783319650708 Круг «целует» кривую с точностью до второго порядка, поэтому получил название соприкасающегося круга (от латинского слова «поцелуй»).

[omnibus-13] Фукс, Дмитрий ; Табачников, Серж (2007), Математический омнибус: тридцать лекций по классической математике , Провиденс, Род-Айленд: Американское математическое общество, с. 142, номер домена : 10.1090/mbk/046 , ISBN 978-0-8218-4316-1 , МР 2350979

[arnold-14] Арнольд, VI (2005), «Принцип топологической экономии в алгебраической геометрии», Обзоры по современной математике , Серия лекций Лондонского математического общества, том. 321, Кембридж: Издательство Кембриджского университета, стр. 13–23, doi : 10.1017/CBO9780511614156.003 , MR 2166922 . См., в частности, стр. 15–16 .

[agnesi-15] Jump up to: ^а ^б Аньези, Мария Гаэтана (1748 г.), Аналитические учреждения для использования итальянской молодежи. См., в частности, задачу 3, стр. 380–382 и рис. 135 .

[fermat-16] де Ферма, Пьер (1891), Oevres (на латыни), vol. 1, Готье-Вилларс и др., стр. 280–285

[fmq-17] Рай, Джеймс; Пла, Джозеф; Виадер, Пелегри (2008), «Метод квадратур Ферма» , Revue d'Histoire des Mathématiques , 14 (1): 5–51, MR 2493381

[stigler-18] Jump up to: ^а ^б ^с ^д Стиглер, Стивен М. (август 1974 г.), «Исследования по истории вероятности и статистики. XXXIII. Коши и ведьма Аньези: историческая заметка о распределении Коши», Biometrika , 61 (2): 375–380, doi : 10.1093/biomet/61.2.375 , JSTOR 2334368 , MR 0370838

[19] В своих примечаниях к «Трактату о естественно ускоренном движении» Галилея Гранди ссылался на «ту кривую, которую я описываю в своей книге квадратур [1703], в положении IV, рожденную из стихов, которую я обычно называю Versiera , но на латыни Версория ». См. Галилей, Опера , 3: 393. Новый термин можно найти у Лоренцо Лоренцини, Exercitatio Geometraa , xxxi: «сидеть pro exemplo curva illa, quam Doctissimus magnusque geometra Guido Grandus Versoria nominat».

[truesdell-20] Jump up to: ^а ^б Трусделл, К. (1991), «Исправление и дополнения к «Марии Гаэтане Аньези» », Архив истории точных наук , 43 (4): 385–386, doi : 10.1007/BF00374764 , […] nata da' seni versi , который в моей стране обычно называется Версиера на латыни, но Версория […]

[grandi-21] Гранди, Дж. (1718), «Примечания к трактату Галилея об ускоренном естественном движении», Opera Di Galileo Galilei (на итальянском языке), том. III, Флоренция, с. 393 . Цитируется Стиглером (1974) .

[struik-22] Jump up to: ^а ^б ^с Перевод работы Аньези об этой кривой можно найти в: Струик, Дирк Дж. (1969), Справочник по математике, 1200–1800 , Кембридж, Массачусетс: Издательство Гарвардского университета, стр. 178–180.

[fanfani-23] Пьетро Фанфани , Тосканский словарь , с. 334

[mulcrone-24] Малкроне, Т.Ф. (1957), «Названия кривой Аньези», American Mathematical Monthly , 64 (5): 359–361, doi : 10.2307/2309605 , JSTOR 2309605 , MR 0085163

[singh-25] Сингх, Саймон (1997), Загадка Ферма: эпический поиск решения величайшей в мире математической проблемы , Нью-Йорк: Уокер и компания, стр. 100 , ISBN 0-8027-1331-9 , МР 1491363

[darling-26] Дарлинг, Дэвид (2004), Универсальная книга по математике: от абракадабры до парадоксов Зенона , Хобокен, Нью-Джерси: John Wiley & Sons, стр. 8, ISBN 0-471-27047-4 , МР 2078978

[oed-27] Оксфордский словарь английского языка , Oxford University Press, 2018, witch, n .2, 4(e) , получено 3 июля 2018 г. , 1875 г. Б. Уильямсон Элем. Обращаться. Интегральное исчисление vii. 173 Найдите область между ведьмой Аньези. $xy^{2}=4a^{2}(2a-x)$ и ее асимптота.

[alexander-28] Александр, Дж. Маккензи (2012), «Теория принятия решений встречает ведьму Аньези», Journal of Philosophy , 109 (12): 712–727, doi : 10.5840/jphil20121091233

[runge-29] Купильяри, Антонелла ; ДеТомас, Элизабет (весна 2007 г.), «Разоблачение колдовского поведения функции Рунге», Mathematics and Computer Education , 41 (2): 143–156, ПроКвест 235858817

[spencer-30] Спенсер, Рой К. (сентябрь 1940 г.), «Свойства ведьмы Аньези - применение к подбору формы спектральных линий», Журнал Оптического общества Америки , 30 (9): 415, Бибкод : 1940JOSA ... 30 ..415S , дои : 10.1364/josa.30.000415

[coppin-31] Коппин, Пенсильвания; Брэдли, EF; Финниган, Дж. Дж. (апрель 1994 г.), «Измерения потока над удлиненным хребтом и зависимость его термостабильности: среднее поле», Boundary-Layer Meteorology , 69 (1–2): 173–199, Bibcode : 1994BoLMe..69. .173C , doi : 10.1007/bf00713302 S2CID 119956741. Полезной , общей формой для формы холма является так называемый профиль «Ведьмы Аньези».

[snyder-32] Снайдер, Уильям Х.; Томпсон, Роджер С.; Эскридж, Роберт Э.; Лоусон, Роберт Э.; Кастро, Ян П.; Ли, Джей Ти; Хант, Джулиан CR; Огава, Ясуши (март 1985 г.), «Структура сильно стратифицированного потока над холмами: концепция разделительной линии тока», Journal of Fluid Mechanics , 152 (–1): 249, Бибкод : 1985JFM...152..249S , doi : 10.1017/s0022112085000684 , S2CID 123563729

[lamb-33] Лэмб, Кевин Г. (февраль 1994 г.), «Численное моделирование стратифицированного невязкого течения над гладким препятствием» (PDF) , Journal of Fluid Mechanics , 260 (–1): 1, Bibcode : 1994JFM...260.... 1L , doi : 10.1017/s0022112094003411 , S2CID 49355530 , заархивировано из оригинала (PDF) 6 января 2014 г.

[benjamin-34] Бенджамин, Т. Брук (сентябрь 1967 г.), «Внутренние волны постоянной формы в жидкостях на большой глубине», Journal of Fluid Mechanics , 29 (3): 559, Bibcode : 1967JFM....29..559B , doi : 10.1017 /s002211206700103x , S2CID 123065419

[noonan-35] Нунан, Джули А.; Смит, Роджер К. (сентябрь 1985 г.), «Линейные и слабонелинейные теории внутренних волн в применении к волнам« ипомеи »», Geophysical & Astrophysical Fluid Dynamics , 33 (1–4): 123–143, Бибкод : 1985GApFD..33 ..123N , дои : 10.1080/03091928508245426

[gazette-36] Филлипс, Дэйв (12 сентября 2006 г.), «Местный учитель, автор формулирует математику в книгах» , The Gazette.

[discogs-37] Radius – Witch Of Agnesi (Plutonium Records, 2002) , Discogs , получено 28 мая 2018 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]