Вырождение (математика)

В математике вырожденный случай — это предельный случай класса объектов, который качественно отличается от остального класса (и обычно проще его); ^[1] « Вырождение » — это состояние вырожденного случая. ^[2]

Определения многих классов составных или структурированных объектов часто неявно включают неравенства. Например, углы и длины сторон треугольника предполагаются положительными. Предельные случаи, когда одно или несколько из этих неравенств становятся равенствами, представляют собой вырождения. В случае треугольников треугольник считается вырожденным, если хотя бы одна длина стороны или угол равны нулю. Эквивалентно, он становится «сегментом линии». ^[3]

Зачастую вырожденные случаи являются исключительными случаями, когда происходят изменения обычной размерности или мощности объекта (или некоторой его части). Например, треугольник — это объект размерности два, а вырожденный треугольник содержится в строке , ^[3] что делает его размерность единицей. Это похоже на случай круга, размерность которого уменьшается от двух до нуля по мере того, как он вырождается в точку. ^[1] Другой пример: набор решений системы уравнений , которая зависит от параметров, обычно имеет фиксированную мощность и размерность, но мощность и/или размерность могут быть разными для некоторых исключительных значений, называемых вырожденными случаями. В таком вырожденном случае множество решений называется вырожденным.

Для некоторых классов составных объектов случаи вырождения зависят от специально изучаемых свойств. В частности, класс объектов часто может быть определен или охарактеризован системами уравнений. В большинстве сценариев данный класс объектов может определяться несколькими различными системами уравнений, и эти разные системы уравнений могут приводить к разным вырожденным случаям, характеризуя при этом одни и те же невырожденные случаи. Это может быть причиной того, что не существует общего определения вырождения, несмотря на то, что это понятие широко используется и определяется (при необходимости) в каждой конкретной ситуации.

Таким образом, вырожденный случай имеет особые особенности, которые делают его необщим или особым случаем . Однако не все необщие или частные случаи являются вырожденными. Например, прямоугольные треугольники , равнобедренные треугольники и равносторонние треугольники не являются общими и невырожденными. Фактически, вырожденные случаи часто соответствуют сингулярностям либо в объекте, либо в некотором конфигурационном пространстве . Например, коническое сечение вырождено тогда и только тогда, когда оно имеет особые точки (например, точку, прямую, пересекающиеся прямые). ^[4]

В геометрии [ править ]

Коническое сечение [ править ]

Вырожденная коника — это коническое сечение второй степени ( плоская кривая , определяемая полиномиальным уравнением второй степени), которое не может быть неприводимой кривой .

Точка — это вырожденная окружность , а именно радиус 0. ^[1]
Линия парабола является вырожденным случаем параболы, если лежит на касательной плоскости . В инверсной геометрии линия — это вырожденный случай круга с бесконечным радиусом.
Две параллельные прямые также образуют вырожденную параболу.
можно Отрезок прямой рассматривать как вырожденный случай эллипса, в котором малая полуось стремится к нулю, фокусы — к конечным точкам, а эксцентриситет — к единице.
Круг можно представить как вырожденный эллипс, поскольку эксцентриситет приближается к 0 и фокусы сливаются. ^[1]
Эллипс также может выродиться в одну точку.
Гипербола общими может выродиться в две линии, пересекающиеся в одной точке, через семейство гипербол, у которых эти линии являются асимптотами .

Треугольник [ править ]

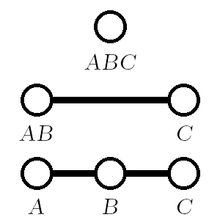
Вырожденный треугольник — это «плоский» треугольник в том смысле, что он содержится в отрезке прямой . Таким образом, он имеет коллинеарные вершины ^[3] и нулевая площадь. Если три вершины попарно различны, они имеют два угла 0° и один угол 180°. Если две вершины равны, они имеют один угол 0° и два неопределенных угла. Если все три вершины равны, все три угла не определены.

Прямоугольник [ править ]

Сегмент прямой — это вырожденный случай прямоугольника , длина стороны которого равна 0.
Для любого непустого подмножества $S\subseteq \{1,2,\ldots ,n\}$ , существует ограниченный вырожденный прямоугольник, выровненный по оси $R\triangleq \left\{\mathbf {x} \in \mathbb {R} ^{n}:x_{i}=c_{i}\ ({\text{for }}i\in S){\text{ and }}a_{i}\leq x_{i}\leq b_{i}\ ({\text{for }}i\notin S)\right\}$ где $\mathbf {x} \triangleq \left[x_{1},x_{2},\ldots ,x_{n}\right]$ и $a i$ , $b i$ , $c i$ постоянны (при этом $a i \leq b i$ для всех $i$ ). Число вырожденных сторон $R$ это количество элементов подмножества $S.$ — Таким образом, может быть всего одна вырожденная «сторона» или столько же, сколько $n$ (в этом случае $R$ сводится к одноточечной точке).

Выпуклый многоугольник [ править ]

Выпуклый многоугольник называется вырожденным, если хотя бы две последовательные стороны совпадают хотя бы частично, или хотя бы одна сторона имеет нулевую длину, или хотя бы один угол равен 180°. Таким образом, вырожденный выпуклый многоугольник с n сторонами выглядит как многоугольник с меньшим количеством сторон. В случае треугольников это определение совпадает с тем, которое было дано выше.

Выпуклый многогранник [ править ]

является Выпуклый многогранник вырожденным, если две соседние грани компланарны или два ребра выровнены. В случае тетраэдра это эквивалентно утверждению, что все его вершины лежат в одной плоскости , что придает ему объем . нулевой

Стандартный тор [ править ]

В контекстах, где разрешено самопересечение, сфера с двойным покрытием представляет собой вырожденный стандартный тор , в котором ось вращения проходит через центр образующей окружности, а не за ее пределами.
Тор вырождается в окружность, когда его меньший радиус становится равным 0.

Сфера [ править ]

Когда радиус сферы обращается в ноль, полученная вырожденная сфера нулевого объема становится точкой .

Другое [ править ]

см . в общем положении . Другие примеры

В другом месте [ править ]

Множество, содержащее одну точку, представляет собой вырожденный континуум .
Такие объекты, как дигон и моногон, можно рассматривать как вырожденные случаи многоугольников : они действительны в общем абстрактном математическом смысле, но не являются частью исходной евклидовой концепции многоугольников.
Случайная величина , которая может принимать только одно значение, имеет вырожденное распределение ; если это значение — действительное число 0, то его плотность вероятности — это дельта-функция Дирака .
Корень он многочлена корней иногда называют вырожденным, если кратный , поскольку в общем случае $все n$ многочлена $n-$ й степени различны. ^[1] Это использование переносится и на собственные задачи: вырожденное собственное значение является кратным корнем характеристического многочлена .
В квантовой механике любая такая кратность собственных значений оператора Гамильтона приводит к вырождению уровней энергии . Обычно любое такое вырождение указывает на некоторую скрытую симметрию в системе.

См. также [ править ]

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Вайсштейн, Эрик В. «Дегенерат» . mathworld.wolfram.com . Проверено 29 ноября 2019 г.
^ «Определение ВЫРОЖДЕНИЯ» . www.merriam-webster.com . Проверено 29 ноября 2019 г.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с «Математические слова: вырожденные» . www.mathwords.com . Проверено 29 ноября 2019 г.
^ «Математические слова: вырожденные конические сечения» . www.mathwords.com . Проверено 29 ноября 2019 г.

[:1-1] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Вайсштейн, Эрик В. «Дегенерат» . mathworld.wolfram.com . Проверено 29 ноября 2019 г.

[2] «Определение ВЫРОЖДЕНИЯ» . www.merriam-webster.com . Проверено 29 ноября 2019 г.

[:2-3] Перейти обратно: Перейти обратно: ^а ^б ^с «Математические слова: вырожденные» . www.mathwords.com . Проверено 29 ноября 2019 г.

[4] «Математические слова: вырожденные конические сечения» . www.mathwords.com . Проверено 29 ноября 2019 г.

[1]

[2]

[3]

[4]