Электрослабое взаимодействие
| Стандартная модель физики элементарных частиц |
|---|
 |
В физике элементарных частиц электрослабое взаимодействие или электрослабая сила — это унифицированное описание двух из четырех известных фундаментальных взаимодействий природы: электромагнетизма (электромагнитного взаимодействия) и слабого взаимодействия . Хотя эти две силы кажутся очень разными при повседневных низких энергиях, теория моделирует их как два разных аспекта одной и той же силы. Выше энергии объединения , порядка 246 ГэВ , [а] они сольются в единую силу. Таким образом, если температура достаточно высокая – примерно 10 15 K – тогда электромагнитная сила и слабое взаимодействие сливаются в объединенное электрослабое взаимодействие. В эпоху кварков (вскоре после Большого взрыва ) электрослабое взаимодействие разделилось на электромагнитное и слабое взаимодействие . Считается, что необходимая температура 10 15 K не наблюдался широко во Вселенной со времен кварковой эпохи, и в настоящее время самая высокая антропогенная температура в тепловом равновесии составляет около 5,5 × 10. 12 К (из Большого адронного коллайдера ).
Шелдон Глэшоу , [1] Привет , Абдус! [2] и Стивен Вайнберг [3] были удостоены Нобелевской премии по физике 1979 года за вклад в объединение слабого и электромагнитного взаимодействия между элементарными частицами , известное как теория Вайнберга-Салама . [4] [5] Существование электрослабых взаимодействий было экспериментально установлено в два этапа: первый — это открытие нейтральных токов при рассеянии нейтрино коллаборацией Гаргамель в 1973 году, а второй — в 1983 году коллаборациями UA1 и UA2 , в ходе которых были открыты W и Z -калибровочные бозоны в протон-антипротонных столкновениях на переоборудованном суперпротонном синхротроне . В 1999 году Герардус 'т Хоофт и Мартинус Вельтман электрослабой теории были удостоены Нобелевской премии за доказательство перенормируемости .
История
[ редактировать ]После того, как эксперимент Ву в 1956 году обнаружил нарушение четности в слабом взаимодействии , начались поиски способа связать слабое и электромагнитное взаимодействия . Продолжая своего научного руководителя Джулиана Швингера работу , Шелдон Глэшоу сначала экспериментировал с введением двух разных симметрий, одной киральной и одной ахиральной, и объединил их так, чтобы их общая симметрия не была нарушена. Это не привело к перенормируемой теории , и ее калибровочную симметрию пришлось нарушать вручную, поскольку спонтанный механизм не был известен, но это предсказало появление новой частицы, Z-бозона . Это не получило особого внимания, поскольку не соответствовало никаким экспериментальным данным.
В 1964 году Салам и Джон Клайв Уорд. [6] имел ту же идею, но предсказал безмассовый фотон и три массивных калибровочных бозона с нарушенной вручную симметрией. Позже, примерно в 1967 году, исследуя спонтанное нарушение симметрии , Вайнберг обнаружил ряд симметрий, предсказывающих появление безмассового нейтрального калибровочного бозона . Первоначально отвергнув такую частицу как бесполезную, он позже понял, что его симметрия порождает электрослабое взаимодействие, и приступил к предсказанию приблизительных масс W- и Z-бозонов . Примечательно, что он предположил, что эта новая теория поддается перенормировке. [3] В 1971 году Жерар 'т Хофт доказал, что спонтанно нарушенные калибровочные симметрии перенормируемы даже с массивными калибровочными бозонами.
Формулировка
[ редактировать ]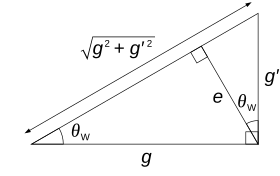
В
и
С
бозоны.
Математически электромагнетизм объединяется со слабыми взаимодействиями как поле Янга–Миллса с SU(2) × U(1) калибровочной группой , которая описывает формальные операции, которые можно применять к электрослабым калибровочным полям без изменения динамики системы. . Этими полями являются слабые изоспиновые поля , W1 W2 и также W3 , слабое поле гиперзаряда B. а Эта инвариантность известна как электрослабая симметрия .
Генераторам ( SU 2) и U(1) присвоены названия слабого изоспина (обозначенного T ) и слабого гиперзаряда (обозначенного Y ) соответственно. Затем они порождают калибровочные бозоны, которые опосредуют электрослабые взаимодействия - три W- бозона слабого изоспина ( W 1 , W 2 и W 3 ) и B -бозон слабого гиперзаряда соответственно, все из которых «изначально» безмассовый. Это еще не физические поля до спонтанного нарушения симметрии и связанного с ним механизма Хиггса .
В Стандартной модели наблюдаемые физические частицы
В ±
и
С 0
бозоны и фотоны рождаются в результате спонтанного нарушения электрослабой симметрии SU(2) × U(1) Y до U(1) em , [б] вызванный механизмом Хиггса (см. также бозон Хиггса ), сложным квантово-полевым явлением, которое «спонтанно» изменяет реализацию симметрии и перестраивает степени свободы. [8] [9] [10] [11]
Электрический заряд возникает как частная линейная комбинация (нетривиальная) Y W (слабый гиперзаряд) и T 3 компонента слабого изоспина ( ), который не взаимодействует с бозоном Хиггса . То есть: бозон Хиггса и электромагнитное поле не влияют друг на друга на уровне фундаментальных сил («уровень дерева»), в то время как любая другая комбинация гиперзаряда и слабого изоспина должна взаимодействовать с бозоном Хиггса. Это вызывает кажущееся разделение между слабым взаимодействием, которое взаимодействует с бозоном Хиггса, и электромагнетизмом, который не взаимодействует. Математически электрический заряд представляет собой определенную комбинацию гиперзаряда и Т 3 , показанную на рисунке.
U(1) em (только группа симметрии электромагнетизма) определяется как группа, порожденная этой специальной линейной комбинацией, а симметрия, описываемая группой U(1) em , не нарушена, поскольку она не взаимодействует напрямую с бозоном Хиггса. . [с]
Вышеописанное спонтанное нарушение симметрии приводит к слиянию бозонов W 3 и B в два разных физических бозона с разными массами –
С 0
бозон и фотон (
с
),
где θW смешивания – угол слабого . Оси, представляющие частицы, по существу только что были повернуты в плоскости ( W 3 , B ) на угол θ W . Это также приводит к несоответствию массы
С 0
и масса
В ±
частицы (обозначаются как m Z и m W соответственно),
Бозоны W1 W2 и , в свою очередь, объединяются , образуя заряженные массивные бозоны.
В ±
:
лагранжиан
[ редактировать ]До нарушения электрослабой симметрии
[ редактировать ]Лагранжиан становится электрослабых взаимодействий делится на четыре части, прежде чем очевидным нарушение электрослабой симметрии :
The термин описывает взаимодействие между тремя векторными бозонами W и векторным бозоном B ,
где ( ) и – тензоры напряженности поля для слабого изоспина и слабого гиперзарядового калибровочного поля.
— кинетический термин для фермионов Стандартной модели. Взаимодействие калибровочных бозонов и фермионов осуществляется через калибровочную ковариантную производную ,
где индекс j суммируется по трем поколениям фермионов; Q , u и d — левые дублетные, правые синглетные верхние и правые синглетные нижние кварковые поля; L . и e — леводуплетное и правостороннее синглетное электронные поля Удар Фейнмана означает сжатие 4-градиента с матрицами Дирака , определяемыми как
а ковариантная производная (исключая глюонное калибровочное поле для сильного взаимодействия ) определяется как
Здесь это слабый гиперзаряд и являются компонентами слабого изоспина.
The термин описывает поле Хиггса и его взаимодействие с самим собой и калибровочными бозонами,
где — вакуумное математическое ожидание.
The термин описывает взаимодействие Юкавы с фермионами,
и генерирует их массы, которые проявляются, когда поле Хиггса приобретает ненулевое вакуумное математическое ожидание, которое обсуждается далее. для являются матрицами связей Юкавы.
После нарушения электрослабой симметрии
[ редактировать ]Лагранжиан реорганизуется, когда поле Хиггса приобретает неисчезающее вакуумное математическое ожидание, продиктованное потенциалом предыдущего раздела. В результате такой переписывания становится очевидным нарушение симметрии. В истории Вселенной считается, что это произошло вскоре после горячего Большого взрыва, когда температура Вселенной составляла 159,5 ± 1,5 ГэВ. [12] (при условии Стандартной модели физики элементарных частиц).
Из-за своей сложности этот лагранжиан лучше всего описать, разбив его на несколько частей следующим образом.
Кинетический член содержит все квадратичные члены лагранжиана, включая динамические члены (частные производные) и массовые члены (заметно отсутствующие в лагранжиане до нарушения симметрии)
где сумма пробегает все фермионы теории (кварки и лептоны), а поля и даны как
с будет заменено соответствующим полем ( ) и f абв структурными константами соответствующей калибровочной группы.
Нейтральный ток и зарядный ток компоненты лагранжиана содержат взаимодействия между фермионами и калибровочными бозонами,
где Электромагнитный ток является
где – электрические заряды фермионов. Нейтральный слабый ток является
где - слабый изоспин фермионов. [д]
Заряженная токовая часть лагранжиана определяется выражением
где – правое синглетное нейтринное поле, а матрица СКМ определяет смешивание массы и слабых собственных состояний кварков. [д]
содержит члены трехточечного и четырехточечного самодействия Хиггса,
содержит взаимодействия Хиггса с калибровочными векторными бозонами,
содержит калибровочные трехточечные самодействия,
содержит калибровочные четырехточечные самодействия,
содержит взаимодействия Юкавы между фермионами и полем Хиггса,
См. также
[ редактировать ]- Электрослабая звезда
- Фундаментальные силы
- История квантовой теории поля
- Стандартная модель (математическая формулировка)
- Датчик унитарности
- Угол Вайнберга
- Теория Янга – Миллса
Примечания
[ редактировать ]- ^ Конкретное число 246 ГэВ принимается за вакуумное математическое ожидание. поля Хиггса (где – константа связи Ферми ).
- ^ Обратите внимание, что U(1) Y и U(1) em являются разными экземплярами общего U(1) : каждая из двух сил получает свою собственную независимую копию унитарной группы.
- ^ Хотя электромагнетизм – например, фотон – не взаимодействует напрямую с бозоном Хиггса , он взаимодействует косвенно , через квантовые флуктуации .
- ^ Перейти обратно: а б Обратите внимание на факторы в формулах слабой связи: эти факторы введены намеренно, чтобы исключить любые левокиральные компоненты спинорных полей. Вот почему электрослабая теория называется « киральной теорией ».
Ссылки
[ редактировать ]- ^ Глэшоу, С. (1959). «Перенормируемость взаимодействий векторных мезонов». Нукл. Физ. 10 , 107.
- ^ Салам, А. ; Уорд, Дж. К. (1959). «Слабые и электромагнитные взаимодействия». Нуово Чименто . 11 (4): 568–577. Бибкод : 1959NCim...11..568S . дои : 10.1007/BF02726525 . S2CID 15889731 .
- ^ Перейти обратно: а б Вайнберг, С. (1967). «Модель лептонов» (PDF) . Физ. Преподобный Летт . 19 (21): 1264–66. Бибкод : 1967PhRvL..19.1264W . дои : 10.1103/PhysRevLett.19.1264 . Архивировано из оригинала (PDF) 12 января 2012 г.
- ^ С. Байс (2005). Уравнения: символы знаний . п. 84 . ISBN 0-674-01967-9 .
- ^ «Нобелевская премия по физике 1979 года» . Нобелевский фонд . Проверено 16 декабря 2008 г.
- ^ Салам, А.; Уорд, Джей Си (ноябрь 1964 г.). «Электромагнитные и слабые взаимодействия» . Письма по физике . 13 (2): 168–171. Бибкод : 1964PhL....13..168S . дои : 10.1016/0031-9163(64)90711-5 .
- ^ Ли, Т.Д. (1981). Физика элементарных частиц и введение в теорию поля .
- ^ Энглерт, Ф.; Браут, Р. (1964). «Нарушенная симметрия и масса калибровочных векторных мезонов» . Письма о физических отзывах . 13 (9): 321–323. Бибкод : 1964PhRvL..13..321E . дои : 10.1103/PhysRevLett.13.321 .
- ^ Хиггс, PW (1964). «Нарушенные симметрии и массы калибровочных бозонов» . Письма о физических отзывах . 13 (16): 508–509. Бибкод : 1964PhRvL..13..508H . doi : 10.1103/PhysRevLett.13.508 .
- ^ Гуральник Г.С.; Хаген, Чехия; Киббл, TWB (1964). «Глобальные законы сохранения и безмассовые частицы» . Письма о физических отзывах . 13 (20): 585–587. Бибкод : 1964PhRvL..13..585G . дои : 10.1103/PhysRevLett.13.585 .
- ^ Гуральник, Г.С. (2009). «История развития Гуральником, Хагеном и Кибблом теории спонтанного нарушения симметрии и калибровочных частиц». Международный журнал современной физики А. 24 (14): 2601–2627. arXiv : 0907.3466 . Бибкод : 2009IJMPA..24.2601G . дои : 10.1142/S0217751X09045431 . S2CID 16298371 .
- ^ Д'Онофрио, Микела; Руммукайнен, Кари (2016). «Стандартная модель кроссовера на решетке». Физ. Преподобный Д. 93 (2): 025003. arXiv : 1508.07161 . Бибкод : 2016PhRvD..93b5003D . дои : 10.1103/PhysRevD.93.025003 . hdl : 10138/159845 . S2CID 119261776 .
Дальнейшее чтение
[ редактировать ]Общие читатели
[ редактировать ]- Б. А. Шумм (2004). Глубокие вещи: захватывающая дух красота физики элементарных частиц . Издательство Университета Джонса Хопкинса. ISBN 0-8018-7971-Х . Передает большую часть Стандартной модели без формальной математики. Очень внимательно относится к слабому взаимодействию.
Тексты
[ редактировать ]- DJ Гриффитс (1987). Введение в элементарные частицы . Джон Уайли и сыновья. ISBN 0-471-60386-4 .
- В. Грейнер; Б. Мюллер (2000). Калибровочная теория слабых взаимодействий . Спрингер. ISBN 3-540-67672-4 .
- Г.Л. Кейн (1987). Современная физика элементарных частиц . Книги Персея . ISBN 0-201-11749-5 .
Статьи
[ редактировать ]- Э. С. Аберс; Б.В. Ли (1973). «Калибровочные теории». Отчеты по физике . 9 (1): 1–141. Бибкод : 1973PhR.....9....1A . дои : 10.1016/0370-1573(73)90027-6 .
- Ю. Хаято; и др. (1999). «Поиск распада протона через p → νK + в большом водном детекторе Черенкова». Physical Review Letters . 83 (8): 1529–1533. arXiv : hep-ex/9904020 . Bibcode : 1999PhRvL..83.1529H . doi : 10.1103/PhysRevLett.83.1529 . S2CID 1183264 09 .
- Дж. Хакс (1991). «Глобальная структура стандартной модели, аномалии и квантование заряда». Физический обзор D . 43 (8): 2709–2717. Бибкод : 1991PhRvD..43.2709H . дои : 10.1103/PhysRevD.43.2709 . ПМИД 10013661 .
- СФ Новаес (2000). «Стандартная модель: Введение». arXiv : hep-ph/0001283 .
- ДП Рой (1999). «Основные составляющие материи и их взаимодействия - отчет о ходе работы». arXiv : hep-ph/9912523 .















































![{\displaystyle {\mathcal {L}}_{\mathrm {C} }=- {\frac {g}{\ {\sqrt {2\;}}\ }}\ \left[\ {\overline {u }}_{i}\ \gamma ^{\mu }\ {\frac {\ 1-\gamma ^{5}\ }{2}}\;M_{ij}^{\mathrm {CKM} }\ d_ {j}+{\overline {\nu }}_{i}\ \gamma ^{\mu }\;{\frac {\ 1-\gamma ^{5}\ }{2}}\;e_{i }\ \right]\ W_{\mu }^{+}+\mathrm {hc} ~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a58fb2388e4f81affcfbb2f9137be3fc21c01d32)







![{\displaystyle {\mathcal {L}}_{\mathrm {WWV} }=-i\ g\ \left[\;\left(\ W_ {\mu \nu }^{+}\ W^{-\ mu }-W^{+\mu }\ W_{\mu \nu }^{-}\ \right)\left(\ A^{\nu }\ \sin \theta _{\mathrm {W} }- Z^{\nu }\ \cos \theta _{\mathrm {W} }\ \right)+W_{\nu }^{-}\ W_{\mu }^{+}\ \left(\ A^ {\mu \nu }\ \sin \theta _ {\mathrm {W} }-Z^{\mu \nu }\ \cos \theta _ {\mathrm {W} }\ \right)\;\right] ~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a692b930d152ed1c16bd24ebede10eb0a7f7c2b)

![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {WWVV} }=-{\frac {\ g^{2}\ }{4}}\ {\Biggl \{}\ &{\Bigl [}\ 2\ W_{\mu }^{+}\ W^{-\mu }+(\ A_{\mu }\ \sin \theta _{\mathrm {W} }-Z_{ \mu }\ \cos \theta _{\mathrm {W} }\ )^{2}\ {\Bigr ]}^{2}\\&-{\Bigl [}\ W_{\mu }^{+ }\ W_{\nu }^{-}+W_{\nu }^{+}\ W_{\mu }^{-}+\left(\ A_{\mu }\ \sin \theta _{\mathrm {W} }-Z_{\mu }\ \cos \theta _{\mathrm {W} }\ \right)\left(\ A_{\nu }\ \sin \theta _{\mathrm {W} }- Z_{\nu }\ \cos \theta _{\mathrm {W} }\ \right)\ {\Bigr ]}^{2}\,{\Biggr \}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7a413ef9a695a06d5c93067c2745e6bfe3d1a3)





