Групповое кольцо

Эта статья об алгебраическом групповом кольце группы. Для случая топологической группы см. групповую алгебру топологической группы .

В алгебре групповое кольцо — это свободный модуль и в то же время кольцо , построенное естественным образом из любого данного кольца и любой данной группы . Как у свободного модуля, его кольцо скаляров является заданным кольцом, а его базисом является множество элементов данной группы. Как кольцо, его закон сложения является законом свободного модуля, а его умножение расширяет «по линейности» данный групповой закон на базисе. Менее формально, групповое кольцо представляет собой обобщение данной группы путем присоединения к каждому элементу группы «весового коэффициента» из данного кольца.

Если кольцо коммутативно, то групповое кольцо также называется групповой алгеброй , поскольку оно действительно является алгеброй над данным кольцом. Групповая алгебра над полем имеет дополнительную структуру алгебры Хопфа ; в этом случае она называется групповой алгеброй Хопфа .

Аппарат групповых колец особенно полезен в теории представлений групп .

Определение

Позволять $G$ — группа, записанная мультипликативно, и пусть $R$ несущий. Групповое кольцо $G$ над $R$, который мы обозначим через $R[G]$или просто $RG$, – множество отображений $f\colon G\to R$ конечной поддержки ( $f(g)$ не равно нулю только для конечного числа элементов $g$), где скалярное произведение модуля $\alpha f$ скаляра $\alpha$ в $R$ и отображение $f$ определяется как отображение $x\mapsto \alpha \cdot f(x)$и групповая сумма модулей двух отображений $f$ и $g$ определяется как отображение $x\mapsto f(x)+g(x)$. Чтобы включить аддитивную группу $R[G]$ в кольцо, определим произведение $f$ и $g$ быть отображением

$x\mapsto \sum _{uv=x}f(u)g(v)=\sum _{u\in G}f(u)g(u^{-1}x).$

Суммирование правомерно, поскольку $f$ и $g$ имеют конечный носитель, и аксиомы колец легко проверяются.

Используются некоторые вариации обозначений и терминологии. В частности, такие отображения, как $f:G\to R$ иногда записаны как так называемые «формальные линейные комбинации элементов $G$ с коэффициентами в $R$":

$\sum _{g\in G}f(g)g,$

или просто

$\sum _{g\in G}f_{g}g.$

Обратите внимание: если кольцо $R$ на самом деле это поле $K$, то модульная структура группового кольца $RG$ на самом деле является векторным пространством над $K$.

Примеры

1. Пусть G = C3 _— циклическая группа порядка 3 с генератором $a$ и идентификационный элемент 1 _G . Элемент r из C [ G ] можно записать как

$r=z_{0}1_{G}+z_{1}a+z_{2}a^{2}\,$

где z0 _​ , z1 _. и z2 _{находятся} в C , числах комплексных Это то же самое, что и кольцо многочленов от переменной $a$ такой, что $a^{3}=a^{0}=1$ т.е. C [ G ] изоморфно кольцу C [ $a$]/ $(a^{3}-1)$.

Написание другого как элемента $s=w_{0}1_{G}+w_{1}a+w_{2}a^{2}$, их сумма

$r+s=(z_{0}+w_{0})1_{G}+(z_{1}+w_{1})a+(z_{2}+w_{2})a^{2}\,$

и их продукт

$rs=(z_{0}w_{0}+z_{1}w_{2}+z_{2}w_{1})1_{G}+(z_{0}w_{1}+z_{1}w_{0}+z_{2}w_{2})a+(z_{0}w_{2}+z_{2}w_{0}+z_{1}w_{1})a^{2}.$

Обратите внимание, что единичный элемент 1 _G группы G индуцирует каноническое вложение кольца коэффициентов (в данном случае C ) в C [ G ]; однако, строго говоря, мультипликативный единичный элемент C [ G ] равен 1⋅1 _G где первая единица происходит от C , а вторая от G. , Аддитивный единичный элемент равен нулю.

Когда G — некоммутативная группа, нужно быть осторожным, чтобы сохранить порядок элементов группы (и не коммутировать их случайно) при умножении членов.

2. Кольцо полиномов Лорана над кольцом R является групповым кольцом бесконечной циклической группы Z над R .

3. Пусть Q — группа кватернионов с элементами $\{e,{\bar {e}},i,{\bar {i}},j,{\bar {j}},k,{\bar {k}}\}$. Рассмотрим групповое кольцо R Q , где R — множество действительных чисел. Произвольный элемент этого группового кольца имеет вид

$x_{1}\cdot e+x_{2}\cdot {\bar {e}}+x_{3}\cdot i+x_{4}\cdot {\bar {i}}+x_{5}\cdot j+x_{6}\cdot {\bar {j}}+x_{7}\cdot k+x_{8}\cdot {\bar {k}}$

где $x_{i}$ это действительное число.

Умножение, как и в любом другом групповом кольце, определяется на основе групповой операции. Например,

${\begin{aligned}{\big (}3\cdot e+{\sqrt {2}}\cdot i{\big )}\left({\frac {1}{2}}\cdot {\bar {j}}\right)&=(3\cdot e)\left({\frac {1}{2}}\cdot {\bar {j}}\right)+({\sqrt {2}}\cdot i)\left({\frac {1}{2}}\cdot {\bar {j}}\right)\\&={\frac {3}{2}}\cdot {\big (}(e)({\bar {j}}){\big )}+{\frac {\sqrt {2}}{2}}\cdot {\big (}(i)({\bar {j}}){\big )}\\&={\frac {3}{2}}\cdot {\bar {j}}+{\frac {\sqrt {2}}{2}}\cdot {\bar {k}}\end{aligned}}.$

Обратите внимание, что R Q что тело кватернионов над R. — это не то же самое , Это связано с тем, что тело кватернионов удовлетворяет дополнительным соотношениям в кольце, например $-1\cdot i=-i$, тогда как в групповом кольце R Q , $-1\cdot i$ не равен $1\cdot {\bar {i}}$. Точнее, групповое кольцо R Q имеет размерность 8 как вещественное векторное пространство , а тело кватернионов имеет размерность 4 как вещественное векторное пространство .

4. Другой пример неабелева группового кольца: $\mathbb {Z} [\mathbb {S} _{3}]$ где $\mathbb {S} _{3}$ — симметричная группа из 3 букв. Это не целостная область, поскольку у нас есть $[1-(12)]*[1+(12)]=1-(12)+(12)-(12)(12)=1-1=0$ где элемент $(12)\in \mathbb {S} _{3}$ - это транспозиция , которая меняет местами 1 и 2. Следовательно, групповое кольцо не обязательно должно быть областью целостности, даже если базовое кольцо является областью целостности.

Некоторые основные свойства

Используя 1 для обозначения мультипликативной идентичности кольца R и обозначая групповую единицу через 1 _G , кольцо R [ G изоморфное R , а его группа обратимых элементов содержит подгруппу, изоморфную G. ] содержит подкольцо , Для рассмотрения индикаторной функции {1 _G }, которая представляет собой вектор f, определенный формулой

$f(g)=1\cdot 1_{G}+\sum _{g\not =1_{G}}0\cdot g=\mathbf {1} _{\{1_{G}\}}(g)={\begin{cases}1&g=1_{G}\\0&g\neq 1_{G}\end{cases}},$

множество всех скалярных кратных f является подкольцом кольца R [ G изоморфным R. ] , И если мы сопоставим каждый элемент s группы G с индикаторной функцией { s }, которая представляет собой вектор f, определенный формулой

$f(g)=1\cdot s+\sum _{g\not =s}0\cdot g=\mathbf {1} _{\{s\}}(g)={\begin{cases}1&g=s\\0&g\neq s\end{cases}}$

результирующее отображение является гомоморфизмом инъективной группы (относительно умножения, а не сложения в R [ G ]).

Если R и G оба коммутативны (т. е. R коммутативен, а G — абелева группа ), R [ G ] коммутативен.

Если H — подгруппа группы G , то R [ H ] — подкольцо группы R [ G ]. Аналогично, если S — подкольцо R , S [ G ] — подкольцо R [ G ].

Если G — конечная группа порядка больше 1, то R [ G ] всегда имеет делители нуля . Например, рассмотрим элемент g из G порядка | г | = m > 1. Тогда 1 - g является делителем нуля:

$(1-g)(1+g+\cdots +g^{m-1})=1-g^{m}=1-1=0.$

Например, рассмотрим групповое кольцо Z [ S ₃ ] и элемент порядка 3 g =(123). В этом случае,

$(1-(123))(1+(123)+(132))=1-(123)^{3}=1-1=0.$

Связанный результат: если групповой звонок $K[G]$ является простым , то G не имеет неединичной конечной нормальной подгруппы (в частности, G должна быть бесконечной).

Доказательство. Рассматривая контрапозитив , предположим, что $H$ является нетождественной конечной нормальной подгруппой группы $G$. Брать $a=\sum _{h\in H}h$. С $hH=H$ для любого $h\in H$, мы знаем $ha=a$, поэтому $a^{2}=\sum _{h\in H}ha=|H|a$. принимая $b=|H|\,1-a$, у нас есть $ab=0$. По нормальности $H$, $a$ ездит на работу с базой $K[G]$, и поэтому

$aK[G]b=K[G]ab=0$.

И мы видим это $a,b$ не равны нулю, что показывает $K[G]$ не является простым. Это показывает исходное утверждение.

Групповая алгебра над конечной группой

Групповые алгебры естественным образом возникают в теории групповых представлений конечных групп . Групповая алгебра K [ G ] над полем K по существу является групповым кольцом, в котором поле K занимает место кольца. Как множество и векторное пространство, это свободное векторное пространство на G над полем K . То есть для x в K [ G ]

$x=\sum _{g\in G}a_{g}g.$

Структура алгебры : в векторном пространстве определяется с помощью умножения в группе

$g\cdot h=gh,$

где слева g и h обозначают элементы групповой алгебры, а умножение справа — групповую операцию (обозначается сопоставлением).

Поскольку приведенное выше умножение может сбить с толку, можно также записать векторы K базисные [ G ] как , например, _g (вместо g ), и в этом случае умножение записывается как:

$e_{g}\cdot e_{h}=e_{gh}.$

Интерпретация как функции

Если рассматривать свободное векторное пространство как K -значные функции на G , то алгебраическое умножение представляет собой свертку функций.

Хотя групповую алгебру конечной группы можно отождествить с пространством функций на группе, для бесконечной группы они другие. Групповая алгебра, состоящая из конечных сумм, соответствует функциям группы, которые обращаются в нуль для коконечного числа точек; топологически (с использованием дискретной топологии ) они соответствуют функциям с компактным носителем .

Однако групповая алгебра K [ G ] и пространство функций K ^Г := Hom( G , K ) двойственны: задан элемент групповой алгебры

$x=\sum _{g\in G}a_{g}g$

и функция на группе f : G → K, эти пары дают элемент K через

$(x,f)=\sum _{g\in G}a_{g}f(g),$

что является корректно определенной суммой, поскольку она конечна.

групповой

Принимая K [ G ] за абстрактную алгебру, можно задаться вопросом о представлениях алгебры, действующей в K- векторном пространстве V размерности d . Такое представление

${\tilde {\rho }}:K[G]\rightarrow {\mbox{End}}(V)$

является гомоморфизмом алгебры групповой алгебры в алгебру эндоморфизмов V , который изоморфен кольцу матриц d × d : $\mathrm {End} (V)\cong M_{d}(K)$. это левый K [ G ]-модуль над абелевой группой V. Эквивалентно ,

Соответственно, представление группы

$\rho :G\rightarrow {\mbox{Aut}}(V),$

является групповым гомоморфизмом из G в группу линейных автоморфизмов V , которая изоморфна общей линейной группе обратимых матриц: $\mathrm {Aut} (V)\cong \mathrm {GL} _{d}(K)$. Любое такое представление индуцирует представление алгебры

${\tilde {\rho }}:K[G]\rightarrow {\mbox{End}}(V),$

просто позволив ${\tilde {\rho }}(e_{g})=\rho (g)$ и распространяется линейно. Таким образом, представления группы в точности соответствуют представлениям алгебры, и обе теории по существу эквивалентны.

Обычное представительство

Основная статья: Регулярное представительство

Групповая алгебра является алгеброй над собой; при соответствии представлений над модулями R и R [ G ] оно является регулярным представлением группы.

Написанное как представление, это представление g ↦ ρ _g с действием, заданным формулой $\rho (g)\cdot e_{h}=e_{gh}$, или

$\rho (g)\cdot r=\sum _{h\in G}k_{h}\rho (g)\cdot e_{h}=\sum _{h\in G}k_{h}e_{gh}.$

Полупростое разложение

Размерность векторного пространства K [ G ] как раз равна количеству элементов в группе. Поле K обычно принимают за комплексные числа C или вещественные числа R , так что речь идет о групповых алгебрах C [ G ] или R [ G ].

Групповая алгебра C [ G ] конечной группы над комплексными числами является полупростым кольцом . Этот результат, теорема Машке , позволяет нам понимать C [ G конечное произведение с колец матриц элементами в C. ] как Действительно, если мы перечислим комплексные неприводимые представления группы G как V _k при k = 1, . . . , m , они соответствуют групповым гомоморфизмам $\rho _{k}:G\to \mathrm {Aut} (V_{k})$ и, следовательно, к гомоморфизмам алгебр ${\tilde {\rho }}_{k}:\mathbb {C} [G]\to \mathrm {End} (V_{k})$. Сборка этих отображений дает изоморфизм алгебры

${\tilde {\rho }}:\mathbb {C} [G]\to \bigoplus _{k=1}^{m}\mathrm {End} (V_{k})\cong \bigoplus _{k=1}^{m}M_{d_{k}}(\mathbb {C} ),$

где dk _​ размерность Vk _. — Подалгебра в C [ G ], соответствующая End( Vk _{двусторонний} ), представляет собой идеал, идемпотентом порожденный

$\epsilon _{k}={\frac {d_{k}}{|G|}}\sum _{g\in G}\chi _{k}(g^{-1})\,g,$

где $\chi _{k}(g)=\mathrm {tr} \,\rho _{k}(g)$ является персонажем Vk ​ _. ​Они образуют полную систему ортогональных идемпотентов, так что $\epsilon _{k}^{2}=\epsilon _{k}$, $\epsilon _{j}\epsilon _{k}=0$ для j ≠ k и $1=\epsilon _{1}+\cdots +\epsilon _{m}$. Изоморфизм ${\tilde {\rho }}$ тесно связано с преобразованием Фурье на конечных группах .

Для более общего поля K, если характеристика K , не делит порядок группы G то K [ G ] полупроста. Когда G — конечная абелева группа , групповое кольцо K [G] коммутативно, и его структуру легко выразить через корни из единицы .

Когда K — поле характеристики p, которое делит порядок G , групповое кольцо не является полупростым: оно имеет ненулевой радикал Джекобсона , и это придает соответствующему предмету модульной теории представлений свой собственный, более глубокий характер.

Центр групповой алгебры

Центр групповой алгебры — это набор элементов, которые коммутируют со всеми элементами групповой алгебры:

$\mathrm {Z} (K[G]):=\left\{z\in K[G]:\forall r\in K[G],zr=rz\right\}.$

Центр равен набору функций класса , то есть набору элементов, которые постоянны в каждом классе сопряженности.

$\mathrm {Z} (K[G])=\left\{\sum _{g\in G}a_{g}g:\forall g,h\in G,a_{g}=a_{h^{-1}gh}\right\}.$

Если K = C , набор неприводимых характеров группы G образует ортонормированный базис Z( K [ G ]) относительно скалярного произведения

$\left\langle \sum _{g\in G}a_{g}g,\sum _{g\in G}b_{g}g\right\rangle ={\frac {1}{|G|}}\sum _{g\in G}{\bar {a}}_{g}b_{g}.$

Групповые звонки в бесконечной группе

Гораздо меньше известно о случае, когда G счетно бесконечна или несчетна, и это область активных исследований. Случай, когда R — поле комплексных чисел, вероятно, наиболее изучен. В этом случае Ирвинг Каплански доказал, что если a и b — элементы C [ G ] с ab = 1 , то ba = 1 . Верно ли это, если R — поле положительной характеристики, остается неизвестным.

Давняя гипотеза Капланского (~1940) гласит, что если G — группа без кручения , а K — поле, то групповое кольцо K [ G ] не имеет нетривиальных делителей нуля . Эта гипотеза эквивалентна тому, что [ G ] не имеет нетривиальных нильпотентов при тех же предположениях для K и G. K

Фактически, условие того, что K является полем, можно распространить на любое кольцо, которое можно вложить в область целостности .

Гипотеза остается открытой в полной общности, однако было показано, что некоторые частные случаи групп без кручения удовлетворяют гипотезе о делителях нуля. К ним относятся:

• Уникальные группы продуктов (например, группы, доступные для заказа , в частности бесплатные группы )
• Элементарные аменабельные группы (например, практически абелевы группы )
• Диффузные группы – в частности, группы, свободно действующие изометрически на R -деревьях, и фундаментальные группы поверхностных групп, за исключением фундаментальных групп прямых сумм одной, двух или трех копий проективной плоскости.

Случай, когда G — топологическая группа, более подробно обсуждается в статье Групповая алгебра локально компактной группы .

Теория категорий

Заместитель

Категорически конструкция группового кольца остается сопряженной с « группой единиц »; следующие функторы являются сопряженной парой :

$R[-]\colon \mathbf {Grp} \to R\mathbf {{\text{-}}Alg}$

$(-)^{\times }\colon R\mathbf {{\text{-}}Alg} \to \mathbf {Grp}$

где $R[-]$ переводит группу в ее групповое кольцо над R и $(-)^{\times }$ переводит R -алгебру в ее группу единиц.

Когда R = Z , это дает соединение между категорией групп и категорией колец , а единица присоединения переводит группу G в группу, содержащую тривиальные единицы: G × {±1} = {± g }. В общем, групповые кольца содержат нетривиальные единицы. Если G содержит элементы a и b такие, что $a^{n}=1$ и b не нормализуется $\langle a\rangle$ тогда квадрат

$x=(a-1)b\left(1+a+a^{2}+...+a^{n-1}\right)$

равен нулю, следовательно $(1+x)(1-x)=1$. Элемент 1 + x является единицей бесконечного порядка.

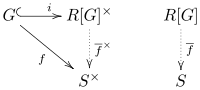
Универсальная собственность

Приведенное выше дополнение выражает универсальное свойство групповых колец. Пусть R — (коммутативное) кольцо, G — группа и S — R -алгебра. Для любого группового гомоморфизма $f:G\to S^{\times }$, существует единственный гомоморфизм R -алгебры ${\overline {f}}:R[G]\to S$ такой, что ${\overline {f}}^{\times }\circ i=f$ где я - включение

${\begin{aligned}i:G&\longrightarrow R[G]\\g&\longmapsto 1_{R}g\end{aligned}}$

Другими словами, ${\overline {f}}$ — единственный гомоморфизм, делающий коммутируемой следующую диаграмму:

Любое другое кольцо, удовлетворяющее этому свойству, канонически изоморфно групповому кольцу.

Алгебра Хопфа

Групповая алгебра K [ G ] имеет естественную структуру алгебры Хопфа . Коумножение определяется формулой $\Delta (g)=g\otimes g$, продолжено линейно, а антипод $S(g)=g^{-1}$, снова продолжено линейно.

Обобщения

Групповая алгебра обобщается до кольца моноида , а затем до алгебры категорий , другим примером которой является алгебра инцидентности .

Фильтрация

Если группа имеет функцию длины (например, если имеется выбор образующих и используется слово метрика , как в группах Кокстера ), то групповое кольцо становится фильтрованной алгеброй .

См. также

• Групповая алгебра локально компактной группы
• Моноидное кольцо
• Догадки Капланского

Теория представлений

• Представительство группы
• Регулярное представительство

Теория категорий

• Категорическая алгебра
• Группа юнитов
• Алгебра инцидентности
• Колчанная алгебра

Ссылки

• А. А. Бовди (2001) [1994], «Групповая алгебра» , Энциклопедия математики , EMS Press
• Милиес, Сезар Польчино; Сегал, Сударшан К. Введение в групповые кольца . Алгебры и приложения, Том 1. Springer, 2002. ISBN   978-1-4020-0238-0
• Чарльз В. Кертис , Ирвинг Райнер . Теория представлений конечных групп и ассоциативных алгебр , Interscience (1962).
• Д. С. Пассман, Алгебраическая структура групповых колец , Wiley (1977)