Теорема о вычетах

В комплексном анализе теорема о вычетах , иногда называемая теоремой Коши о вычетах , является мощным инструментом для вычисления линейных интегралов аналитических функций по замкнутым кривым; его часто можно использовать для вычисления действительных интегралов и бесконечных рядов . Он обобщает интегральную теорему Коши и интегральную формулу Коши . Теорему о вычетах не следует путать со специальными случаями обобщенной теоремы Стокса ; однако последнее можно использовать как составную часть доказательства.

Формулировка теоремы Коши о вычетах

См. также: Остаток (комплексный анализ)

Заявление заключается в следующем:

Иллюстрация обстановки

Позволять $U$ — односвязное открытое подмножество комплексной плоскости , содержащее конечный список точек $a_{1},\ldots ,a_{n},$ $U_{0}=U\smallsetminus \{a_{1},\ldots ,a_{n}\},$ и функция $f$ голоморфный на $U_{0}.$ Сдача в аренду $\gamma$ быть замкнутой спрямляемой кривой в $U_{0},$ и остаток обозначая $f$ в каждой точке $a_{k}$ к $\operatorname {Res} (f,a_{k})$ и витков число $\gamma$ вокруг $a_{k}$ к $\operatorname {I} (\gamma ,a_{k}),$ линейный интеграл от $f$ вокруг $\gamma$ равно $2\pi i$ умноженное на сумму остатков, каждый из которых учитывается столько раз, сколько $\gamma$ обходит соответствующую точку:

$$\oint _{\gamma }f(z)\,dz=2\pi i\sum _{k=1}^{n}\operatorname {I} (\gamma ,a_{k})\operatorname {Res} (f,a_{k}).$$

Если $\gamma$ — положительно ориентированная простая замкнутая кривая , $\operatorname {I} (\gamma ,a_{k})$ является $1$ если $a_{k}$ находится внутри $\gamma$ и $0$ если нет, то поэтому

$$\oint _{\gamma }f(z)\,dz=2\pi i\sum \operatorname {Res} (f,a_{k})$$

с суммой выше этих $a_{k}$ внутри $\gamma .$

Связь теоремы о вычетах с теоремой Стокса определяется теоремой Жордана о кривой . Общая плоская кривая γ должна быть сначала сведена к набору простых замкнутых кривых $\{\gamma _{i}\}$ общая сумма которых эквивалентна $\gamma$ в целях интеграции; это сводит задачу к нахождению интеграла от $f\,dz$ по жордановой кривой $\gamma _{i}$ с интерьером $V.$ Требование, чтобы $f$ быть голоморфным на $U_{0}=U\smallsetminus \{a_{k}\}$ эквивалентно утверждению, что внешняя производная $d(f\,dz)=0$ на $U_{0}.$ Таким образом, если две плоские области $V$ и $W$ из $U$ включить одно и то же подмножество $\{a_{j}\}$ из $\{a_{k}\},$ регионы $V\smallsetminus W$ и $W\smallsetminus V$ лежать целиком в $U_{0},$ следовательно

$$\int _{V\smallsetminus W}d(f\,dz)-\int _{W\smallsetminus V}d(f\,dz)$$

корректно определен и равен нулю. Следовательно, контурный интеграл от $f\,dz$ вдоль $\gamma _{j}=\partial V$ равен сумме набора интегралов по путям $\gamma _{j},$ каждый из которых охватывает сколь угодно малую область вокруг одного $a_{j}$ — остатки $f$ (с точностью до условного коэффициента $2\pi i$ в $\{a_{j}\}.$ Подведение итогов $\{\gamma _{j}\},$ восстанавливаем окончательное выражение контурного интеграла через номера витков $\{\operatorname {I} (\gamma ,a_{k})\}.$

Для вычисления действительных интегралов теорема о вычетах используется следующим образом: подынтегральное выражение расширяется на комплексную плоскость и вычисляются его вычеты (что обычно несложно), а часть вещественной оси расширяется до замкнутой кривой. путем прикрепления полукруга в верхней или нижней полуплоскости, образуя полукруг. Интеграл по этой кривой затем можно вычислить с помощью теоремы о вычетах. Часто часть интеграла в форме полукруга будет стремиться к нулю по мере увеличения радиуса полукруга, оставляя только часть интеграла по действительной оси, которая нас изначально интересовала.

Расчет остатков

Этот раздел представляет собой отрывок из книги Остаток (комплексный анализ) § Расчет остатков . [ редактировать ]

Предположим, проколотый диск D = { z : 0 < | г - с | < R } в комплексной плоскости задано, а f — голоморфная функция , определенная (по крайней мере) на D . Остаток Res( f , c ) от f в точке c является коэффициентом a ₋₁ числа ( z − c ) ⁻¹ в в ряд Лорана разложении f вокруг c . Существуют различные методы вычисления этой величины, и выбор того, какой метод использовать, зависит от рассматриваемой функции и природы особенности.

По теореме о вычетах имеем:

$\operatorname {Res} (f,c)={1 \over 2\pi i}\oint _{\gamma }f(z)\,dz$

где γ очерчивает окружность вокруг c против часовой стрелки и не проходит через нее и не содержит в себе других особенностей. Мы можем выбрать путь γ как круг радиуса ε вокруг c. Поскольку ε может быть настолько малым, насколько мы хотим, его можно заставить содержать только особенность c из-за природы изолированных особенностей. Это можно использовать для расчета в тех случаях, когда интеграл можно вычислить напрямую, но обычно вычеты используются для упрощения расчета интегралов, а не наоборот.

Устранимые особенности

Если функцию f можно продолжить до голоморфной функции на всем круге $|y-c|<R$, то Res( f , c ) = 0. Обратное, вообще говоря, неверно.

Простые столбы

Если c является простым полюсом f f , остаток : определяется следующим образом

$\operatorname {Res} (f,c)=\lim _{z\to c}(z-c)f(z).$

Если этот предел не существует, то вместо этого f имеет существенную особенность в точке c . Если предел равен 0, то f либо аналитична в точке c , либо имеет там устранимую особенность. Если предел равен бесконечности, то порядок полюса больше 1.

Возможно, функцию f можно выразить как частное двух функций: $f(z)={\frac {g(z)}{h(z)}}$, где g и h — голоморфные функции в окрестности c : , с h ( c ) = 0 и h( c ) ≠ 0. В таком случае правило Лопиталя можно использовать для упрощения приведенной выше формулы до

${\begin{aligned}\operatorname {Res} (f,c)&=\lim _{z\to c}(z-c)f(z)=\lim _{z\to c}{\frac {zg(z)-cg(z)}{h(z)}}\\[4pt]&=\lim _{z\to c}{\frac {g(z)+zg'(z)-cg'(z)}{h'(z)}}={\frac {g(c)}{h'(c)}}.\end{aligned}}$

Предельная формула для полюсов высшего порядка

В более общем смысле, если c является полюсом порядка n , то остаток f вокруг z = c можно найти по формуле:

$\operatorname {Res} (f,c)={\frac {1}{(n-1)!}}\lim _{z\to c}{\frac {d^{n-1}}{dz^{n-1}}}\left((z-c)^{n}f(z)\right).$

Эта формула может быть очень полезна при определении вычетов для полюсов низкого порядка. Для полюсов более высокого порядка расчеты могут стать неуправляемыми, и расширение серии обычно проще. Для существенных особенностей такой простой формулы не существует, и вычеты обычно следует брать непосредственно из разложения в ряд.

Остаток на бесконечности

В общем случае остаток на бесконечности определяется как:

$\operatorname {Res} (f(z),\infty )=-\operatorname {Res} \left({\frac {1}{z^{2}}}f\left({\frac {1}{z}}\right),0\right).$

Если выполняется следующее условие:

$\lim _{|z|\to \infty }f(z)=0,$

тогда остаток на бесконечности можно вычислить по следующей формуле:

$\operatorname {Res} (f,\infty )=-\lim _{|z|\to \infty }z\cdot f(z).$

Если вместо этого

$\lim _{|z|\to \infty }f(z)=c\neq 0,$

тогда остаток на бесконечности равен

$\operatorname {Res} (f,\infty )=\lim _{|z|\to \infty }z^{2}\cdot f'(z).$

Для функций, мероморфных на всей комплексной плоскости с конечным числом особенностей, сумма вычетов в (обязательно) изолированных особенностях плюс вычет на бесконечности равна нулю, что дает:

$\operatorname {Res} (f(z),\infty )=-\sum _{k}\operatorname {Res} (f(z),a_{k}).$

Методы серии

Если части или всю функцию можно разложить в ряд Тейлора или ряд Лорана , что может быть возможно, если части или вся функция имеет стандартное разложение в ряд, то вычисление остатка существенно проще, чем другими методами. Остаток функции просто определяется коэффициентом при $(z-c)^{-1}$ в в ряд Лорана . разложении функции

Примеры

Интеграл по вещественной оси

Интеграл $$\int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx$$

Контур С. ​

возникает в теории вероятностей при вычислении характеристической функции распределения Коши . Он не поддается методам элементарного исчисления , но его можно оценить, выразив его как предел контурных интегралов .

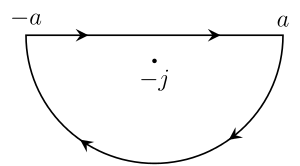
Предположим t > 0 и определим контур C , который идет вдоль вещественной линии от − a до a , а затем против часовой стрелки по полукругу с центром в точке 0 от a до − a . Возьмем a больше 1, чтобы мнимая единица i была заключена в кривую. Теперь рассмотрим контурный интеграл $$\int _{C}{f(z)}\,dz=\int _{C}{\frac {e^{itz}}{z^{2}+1}}\,dz.$$

Поскольку е ^это является целой функцией (не имеющей особенностей ни в одной точке комплексной плоскости), эта функция имеет особенности только там, где знаменатель z ² +1 это ноль. Поскольку z ² + 1 знак равно ( z + я )( z - я ) , это происходит только там, где z знак равно я или z знак равно - я . Только одна из этих точек находится в области, ограниченной этим контуром. Поскольку f ( z ) ​ $${\begin{aligned}{\frac {e^{itz}}{z^{2}+1}}&={\frac {e^{itz}}{2i}}\left({\frac {1}{z-i}}-{\frac {1}{z+i}}\right)\\&={\frac {e^{itz}}{2i(z-i)}}-{\frac {e^{itz}}{2i(z+i)}},\end{aligned}}$$остаток ​ f = ( z ) точке z равен i в $$\operatorname {Res} _{z=i}f(z)={\frac {e^{-t}}{2i}}.$$

Тогда согласно теореме о вычетах имеем $$\int _{C}f(z)\,dz=2\pi i\cdot \operatorname {Res} \limits _{z=i}f(z)=2\pi i{\frac {e^{-t}}{2i}}=\pi e^{-t}.$$

Контур C можно разбить на прямую часть и изогнутую дугу, так что $$\int _{\mathrm {straight} }f(z)\,dz+\int _{\mathrm {arc} }f(z)\,dz=\pi e^{-t}$$и таким образом $$\int _{-a}^{a}f(z)\,dz=\pi e^{-t}-\int _{\mathrm {arc} }f(z)\,dz.$$

Используя некоторые оценки , мы имеем $$\left|\int _{\mathrm {arc} }{\frac {e^{itz}}{z^{2}+1}}\,dz\right|\leq \pi a\cdot \sup _{\text{arc}}\left|{\frac {e^{itz}}{z^{2}+1}}\right|\leq \pi a\cdot \sup _{\text{arc}}{\frac {1}{|z^{2}+1|}}\leq {\frac {\pi a}{a^{2}-1}},$$и $$\lim _{a\to \infty }{\frac {\pi a}{a^{2}-1}}=0.$$

Оценка числителя следует, поскольку t > 0 , а для комплексных чисел z вдоль дуги (которая лежит в верхней полуплоскости) аргумент φ числа z лежит между 0 и π . Так, $$\left|e^{itz}\right|=\left|e^{it|z|(\cos \varphi +i\sin \varphi )}\right|=\left|e^{-t|z|\sin \varphi +it|z|\cos \varphi }\right|=e^{-t|z|\sin \varphi }\leq 1.$$

Поэтому, $$\int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{-t}.$$

Если t < 0 , то аналогичный аргумент с дугой C ′, которая вьется вокруг − i, а не i, показывает, что

Контур C ′ .

$$\int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{t},$$

и наконец у нас есть $$\int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{-\left|t\right|}.$$

(Если t = 0 , то интеграл немедленно поддается элементарному исчислению и его значение равно π .)

Оценка дзета-функций

Тот факт, что π cot( πz ) имеет простые полюса с вычетом 1 в каждом целом числе, можно использовать для вычисления суммы $$\sum _{n=-\infty }^{\infty }f(n).$$

Рассмотрим, например, f ( z ) = z ⁻² . Пусть Γ _{N —} прямоугольник, являющийся границей [− N − ⁠ 1 / 2 ⁠ , N + ⁠ 1 / 2 ⁠ ] ² с положительной ориентацией, с целым числом N . По формуле остатка

$${\frac {1}{2\pi i}}\int _{\Gamma _{N}}f(z)\pi \cot(\pi z)\,dz=\operatorname {Res} \limits _{z=0}+\sum _{n=-N \atop n\neq 0}^{N}n^{-2}.$$

Левая часть стремится к нулю при N → ∞, поскольку $|\cot(\pi z)|$ равномерно ограничен по контуру благодаря использованию $x=\pm \left({\frac {1}{2}}+N\right)$ на левой и правой стороне контура, поэтому подынтегральная функция имеет порядок $O(N^{-2})$ по всему контуру. С другой стороны,

$${\frac {z}{2}}\cot \left({\frac {z}{2}}\right)=1-B_{2}{\frac {z^{2}}{2!}}+\cdots$$ где число Бернулли $B_{2}={\frac {1}{6}}.$

(Фактически, ⁠ z / 2 ⁠ детская кроватка( ⁠ z / 2 ⁠ ) = ⁠ из / 1 - е ^{− iz} ⁠ − ⁠ iz / 2 ⁠ .) Таким образом, остаток Res _{z =0} равен − ⁠ π ² / 3 ⁠ . Делаем вывод:

$$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}$$что является доказательством Базельской проблемы .

Один и тот же аргумент работает для всех $f(x)=x^{-2n}$ где $n$ является положительным целым числом, что дает нам $$\zeta (2n)={\frac {(-1)^{n+1}B_{2n}(2\pi )^{2n}}{2(2n)!}}.$$Трюк не работает, когда $f(x)=x^{-2n-1}$, так как в этом случае вычет в нуле обращается в нуль, и мы получаем бесполезное тождество $0+\zeta (2n+1)-\zeta (2n+1)=0$.

Оценка серии Эйзенштейна

Тот же прием можно использовать для определения суммы ряда Эйзенштейна : $$\pi \cot(\pi z)=\lim _{N\to \infty }\sum _{n=-N}^{N}(z-n)^{-1}.$$

Доказательство

Выберите произвольный $w\in \mathbb {C} \setminus \mathbb {Z}$. Как и выше, определите

$$g(z):={\frac {1}{w-z}}\pi \cot(\pi z)$$

По теореме Коши о вычетах для всех $N$ достаточно большой, такой, что $\Gamma _{N}$ окружает $w$,

$${\frac {1}{2\pi i}}\oint _{\Gamma _{N}}g(z)dz=-\pi \cot(\pi z)+\sum _{n=-N}^{N}{\frac {1}{z-n}}$$

Осталось доказать, что интеграл сходится к нулю. С $\pi \cot(\pi z)/z$ является четной функцией, и $\Gamma _{N}$ симметричен относительно начала координат, имеем $\oint _{\Gamma _{N}}\pi \cot(\pi z)/zdz=0$, и так

$$\oint _{\Gamma _{N}}g(z)dz=\oint _{\Gamma _{N}}\left({\frac {1}{z}}+{\frac {1}{w-z}}\right)\pi \cot(\pi z)dz=-w\oint _{\Gamma _{N}}{\frac {1}{z(z-w)}}\pi \cot(\pi z)dz=O(1/N)$$

См. также

• Остаток (комплексный анализ)
• Интегральная формула Коши
• Основная теорема Глассера
• Лемма Джордана
• Методы контурного интегрирования
• Теорема Мореры
• Теорема Нахбина
• Остаток на бесконечности
• Логарифмическая форма

Ссылки

• Альфорс, Ларс (1979). Комплексный анализ . МакГроу Хилл. ISBN  0-07-085008-9 .
• Линделеф, Эрнст Л. (1905). Вычисление вычетов и его приложения к теории функций (на французском языке). Издания Жака Габе (опубликовано в 1989 г.). ISBN  2-87647-060-8 .
• Митринович, Драгослав; Кечкич, Йован (1984). Метод вычетов Коши: Теория и приложения . Издательство Д. Рейделя. ISBN  90-277-1623-4 .
• Уиттакер, ET ; Уотсон, Дж.Н. (1920). Курс современного анализа (3-е изд.). Издательство Кембриджского университета.

Внешние ссылки

• «Интегральная теорема Коши» , Энциклопедия математики , EMS Press , 2001 [1994]
• Теорема о вычетах в MathWorld