Метод Датара – Мэтьюза для реальной оценки опционов

Метод Датара – Мэтьюза ( Метод ДМ ) Это метод реальной оценки опционов . Этот метод обеспечивает простой способ определить реальную стоимость опциона проекта, просто используя среднее значение положительных результатов проекта. Этот метод можно понимать как расширение чистой приведенной стоимости многосценарной модели Монте-Карло (NPV) с поправкой на неприятие риска и принятие экономических решений. В этом методе используется информация, которая естественным образом возникает при стандартной дисконтированной денежной потоке (DCF), или NPV , финансовой оценке проекта. Он был создан в 2000 году Винаем Датаром, профессором Университета Сиэтла ; и Скотт Х. Мэтьюз, технический сотрудник компании Boeing .

Метод

Рис. 1 Типичный денежный поток проекта с неопределенностью

Математическое уравнение метода DM показано ниже. Этот метод фиксирует реальную стоимость опциона путем дисконтирования распределения операционной прибыли по R , ставке рыночного риска, и дисконтирования распределения дискреционных инвестиций по r , безрисковой ставке, прежде чем рассчитывать ожидаемую выплату. В этом случае стоимость опциона представляет собой ожидаемое значение максимума разницы между двумя дисконтированными распределениями или ноль. Рис. 1.

$C_{0}=E\left[\max \left({\tilde {S}}_{T}e^{-Rt}-{\tilde {X}}_{T}e^{-rt},0\right)\right]$

• ${\tilde {S}}_{T}$ — случайная величина, будущие выгоды или операционную прибыль в момент времени T. представляющая Текущая оценка ​ ${\tilde {S}}_{T}$ использует R , ставку дисконтирования, соответствующую уровню риска ${\tilde {S}}_{T},$ ${\tilde {S}}_{0}={\tilde {S}}_{T}e^{-RT}.$ R — требуемая норма прибыли для участия на целевом рынке, иногда называемая барьерной ставкой .
• ${\tilde {X}}_{T}$ — случайная величина, представляющая цену исполнения . Текущая оценка ${\tilde {X}}_{T}$ использует r , ставка соответствует риску капитальных вложений ${\tilde {X}}_{T},$ ${\tilde {X}}_{0}={\tilde {X}}_{T}e^{-rT}.$ Во многих приложениях обобщенных опционов используется безрисковая ставка дисконтирования. Однако можно рассмотреть и другие ставки дисконтирования, например ставку по корпоративным облигациям, особенно если приложение представляет собой внутренний проект по разработке корпоративного продукта.
• $C_{0}$ — реальная стоимость опциона для одноэтапного проекта. Стоимость опциона можно понимать как ожидаемую стоимость разницы двух распределений текущей стоимости с экономически рациональным порогом, ограничивающим потери с поправкой на риск. Это значение также может быть выражено как стохастическое распределение.

Дифференциальная ставка дисконтирования для R и r неявно позволяет методу DM учитывать базовый риск. Если R > r , то опцион будет не склонен к риску , что характерно как для финансовых, так и для реальных опционов. Если R < r , то опцион будет рискованным. Если R = r , то это называется нейтральным к риску вариантом и имеет параллели с анализом типа NPV с принятием решений, таким как деревья решений . Метод DM дает те же результаты, что и модели Блэка-Шоулза и варианты биномиальной решетки , при условии, что используются те же входные данные и методы дисконтирования. Таким образом, эта неторгуемая стоимость реального опциона зависит от восприятия риска оценщиком в отношении рыночного актива по сравнению с частным инвестиционным активом.

Метод DM удобен для использования в приложениях реальных опционов, поскольку, в отличие от некоторых других моделей опционов, он не требует значения сигмы (меры неопределенности) или S ₀ (сегодняшняя стоимость проекта), оба из которых трудно определить. получение результатов для проектов разработки новых продуктов; см . далее в разделе «Оценка реальных опционов» . Наконец, метод DM использует реальные значения любого типа распределения , избегая требования преобразования в нейтральные к риску значения и ограничения логарифмически нормального распределения ; см . далее в разделе «Методы Монте-Карло» для определения цены опционов .

Были разработаны расширения метода для оценки других реальных опционов, таких как гарантия контракта (опцион пут), многоэтапный вариант , ранний запуск (американский опцион) и другие.

Выполнение

Метод DM может быть реализован с использованием моделирования Монте-Карло . или в упрощенной алгебраической или другой форме (см. опцию «Диапазон» ниже).

Используя моделирование, для каждого образца движок извлекает случайную величину из обоих ${\tilde {S}}_{T}{\text{ and }}{\tilde {X}}_{T},$ вычисляет их текущую стоимость и принимает разницу. Рис. 2А. Значение разницы сравнивается с нулем, определяется максимальное из двух значений, а полученное значение записывается механизмом моделирования. Здесь, отражая необязательность, присущую проекту, прогноз чистого отрицательного значения результата соответствует заброшенному проекту и имеет нулевое значение. Рис. 2Б. Полученные значения создают распределение выигрыша, представляющее экономически рациональный набор правдоподобных прогнозов дисконтированной стоимости проекта в момент времени T ₀ .

Рис. 2А. Распределение приведенной стоимости чистой прибыли.

Рис. 2Б Рациональное распределение решений

Рис. 2C. Распределение выплат и стоимость опциона.

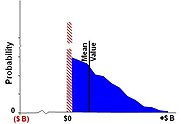
Когда записано достаточное количество выигрышей, обычно несколько сотен, рассчитывается среднее или ожидаемое значение распределения выигрышей. Рис. 2В. Стоимость опциона — это ожидаемая стоимость, первый момент всех положительных NPV и нулей распределения выигрыша.

Простая интерпретация такова:

${\text{Real option value}}={\text{average}}\left[\max \left({\text{operating profit}}-{\text{launch costs}}\right),0)\right]$

где операционная прибыль и затраты на запуск представляют собой соответствующим образом дисконтированный диапазон денежных потоков к моменту времени T ₀ .

Стоимость опциона также можно понимать как распределение ( ${\tilde {C}}_{0}$), отражающий неопределенность основных переменных.

Варианты опций DM

Алгебраическая логнормальная форма

Реальный опцион DM можно рассматривать как обобщенную форму оценки опциона. Его моделирование дает усеченное распределение текущей стоимости, среднее значение которого интерпретируется как стоимость опциона. При определенных граничных условиях опцион DM можно алгебраически переформулировать как условное ожидание логарифмически нормального распределения, аналогичного форме и характеристикам типичного финансового опциона, такого как европейский одноэтапный финансовый опцион Блэка-Шоулза. В этом разделе показано преобразование реального опциона DM в его алгебраическую логнормальную форму и его связь с формулой финансового опциона Блэка-Шоулза. Этот процесс освещает некоторые из более технических элементов формулировки опциона, тем самым обеспечивая дальнейшее понимание основных концепций.

Рис. 3. Понятие условного распределения вероятностей и среднего значения хвоста.

Логнормальная форма метода DM остается простой концепцией, основанной на тех же вычислительных процедурах, что и форма моделирования. Это условное ожидание дисконтированного прогнозируемого распределения будущей стоимости, ${\tilde {S}}_{T}$, за вычетом заранее определенной стоимости покупки (цены исполнения или стоимости запуска), ${\bar {X}}_{T}$, (смоделированное в этом примере как скалярное значение), умноженное на вероятность того, что это усеченное распределение превышает пороговое значение — номинально 0. Условное ожидание — это ожидаемое значение усеченного распределения ( среднее значение хвоста), MT , вычисленное по отношению к его условному распределению вероятностей (рис. 3).

Рис. 4. Дифференцированное во времени дисконтирование, по-видимому, смещает X относительно S.

Процедура расчета опциона оценивает инвестицию в проект (покупку опциона) C ₀ в T ₀ . Для варианта DM дифференцированное по времени дисконтирование ( R и r ) приводит к очевидному сдвигу распределения результатов прогнозируемой стоимости, ${\tilde {S}}$, относительно ${\tilde {X}}$, или скалярное среднее ${\bar {X}}$ в примере, показанном на рис. 4. Этот относительный сдвиг устанавливает условное ожидание усеченного распределения при T ₀ .

В логнормальном распределении будущей стоимости проекта ${\tilde {S}}_{T}$, оба средние, ${\bar {S}}_{T}$и стандартное отклонение, $SD_{T}$, необходимо указать. Стандартное отклонение, $SD_{T}$, распределения ${\tilde {S}}_{T}$ пропорционально дисконтируется вместе с распределением, $SD_{0}=SD_{T}e^{-RT}.$

Параметры $\sigma {\text{ and }}\mu$, логнормального значения при T ₀ можно получить из значений $SD_{0}{\text{ and }}S_{0}$ соответственно, как:

$\sigma ={\sqrt {\ln \left[1+\left({\tfrac {SD}{S}}\right)^{2}\right]}}{\text{ where }}{\tfrac {SD}{S}}={\tfrac {SD_{0}}{S_{0}}}={\tfrac {SD_{T}}{S_{T}}}$

$\mu =\ln \left({\tfrac {S_{0}}{\sqrt {1+\left({\tfrac {SD}{S}}\right)^{2}}}}\right)=\ln S_{0}-0.5\ln \left[1+\left({\tfrac {SD}{S}}\right)^{2}\right]=\ln S_{0}-0.5\sigma ^{2}.$

Условное ожидание результата со скидкой — это среднее значение хвоста MT :

$E\left[{\tilde {S}}\mid {\tilde {S}}\geq X\right]=S_{0}\left[{\tfrac {N\left({\tfrac {\mu +\sigma ^{2}-\ln X_{0}}{\sigma }}\right)}{N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right)}}\right]{\text{ where }}N(\cdot )$ — кумулятивная функция распределения стандартного нормального распределения (N(0,1)).

Вероятность того, что проект окупится и будет запущен («исполнен») равна $N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right).$

Стоимость инвестиций в проект (опцион) составляет:

$C_{0}=\left\{S_{0}\left[{\tfrac {N\left({\tfrac {\sigma ^{2}+\mu -\ln X_{0}}{\sigma }}\right)}{N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right)}}\right]-X_{0}\right\}N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right).$

Используемая логнормальная математика может быть обременительной и непрозрачной для некоторых методов ведения бизнеса внутри корпорации. Однако некоторые упрощения могут облегчить это бремя и обеспечить ясность, не жертвуя при этом правильностью расчета опциона. Одним из упрощений является использование стандартного нормального распределения , также известного как Z-распределение, которое имеет среднее значение 0 и стандартное отклонение 1. Обычной практикой является преобразование нормального распределения в стандартное нормальное, а затем использование стандартного нормального распределения. обычная таблица для нахождения значений вероятностей.

Определите как стандартную нормальную переменную : $Z={\tfrac {\left(\ln X_{0}-\mu \right)}{\sigma }}.$

Условное ожидание результата дисконтированной стоимости равно:

$S_{0}\left[{\tfrac {N\left({\tfrac {\mu +\sigma ^{2}-\ln X_{0}}{\sigma }}\right)}{N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right)}}\right]=S_{0}\left[{\tfrac {N\left(\sigma -Z\right)}{N\left(-Z\right)}}\right].$

Тогда вероятность того, что проект окупится и будет запущен («исполнен»), равна: $N\left({\tfrac {\mu -\ln X_{0}}{\sigma }}\right)=N\left(-Z\right).$

Значение опции Lognormal Datar-Mathews упрощается до:

$C_{\text{DM}}=\left\{S_{0}\left[{\tfrac {N\left(\sigma -Z\right)}{N\left(-Z\right)}}\right]-X_{0}\right\}N\left(-Z\right)=S_{0}N\left(\sigma -Z\right)-X_{0}N\left(-Z\right).$

Преобразование к варианту Блэка-Шоулза

Формула опциона Блэка-Шоулза (а также биномиальная решетка ) представляет собой частный случай моделируемого реального опциона DM. С небольшими, но заметными различиями логарифмическая форма опциона DM может быть алгебраически преобразована в формулу опциона Блэка-Шоулза. Реальная оценка опциона основана на аппроксимации распределения результатов будущей стоимости, которое может быть логарифмически нормальным в момент времени T _T, прогнозируемого (дисконтированного) до T ₀ . Напротив, метод Блэка-Шоулза основан на логарифмически нормальном распределении, прогнозируемом на основе исторической доходности активов до настоящего времени T ₀ . Анализ этих исторических тенденций приводит к расчету, названному коэффициентом волатильности (финансов) . Для Блэка-Шоулза (BS) коэффициент волатильности равен $\sigma _{BS}{\sqrt {T}}$.

Следующее логнормальное распределение со стандартным отклонением $\sigma$ заменяется коэффициентом волатильности $\sigma _{BS}{\sqrt {T}}$.

$\left(\sigma -Z\right)=\sigma -{\tfrac {\left(\ln X_{0}-\mu \right)}{\sigma }}=\ln S_{0}-0.5\ln \left[1+\left({\tfrac {SD}{S}}\right)^{2}\right]={\tfrac {\left[\ln \left({\tfrac {S_{0}}{X_{T}}}\right)+\left(r+{\tfrac {\sigma _{\text{BS}}^{2}}{2}}\right)T\right]}{\left(\sigma _{\text{BS}}{\sqrt {T}}\right)}}=d_{1}{\text{ where }}\ln X_{T}=\ln X_{0}-rT$

$\left(-Z\right)=-{\tfrac {\left(\ln X_{0}-\mu \right)}{\sigma }}={\tfrac {\left[\left(\ln S_{0}-0.5\sigma ^{2}\right)-\ln X_{0}\right]}{\sigma }}={\tfrac {\left[\ln \left({\tfrac {S_{0}}{X_{T}}}\right)+\left(r-{\tfrac {\sigma _{\text{BS}}^{2}}{2}}\right)T\right]}{\left(\sigma _{\text{BS}}{\sqrt {T}}\right)}}=d_{1}-\sigma _{\text{BS}}{\sqrt {T}}=d_{2}$

Стоимость опциона Блэка-Шоулза упрощается до привычной формы:

$C_{\text{BS}}=SN\left(d_{1}\right)-X_{T}e^{-rT}N\left(d_{2}\right)$

Рис. 5. Слева: Сравнение схем Блэка-Шоулза и Датар-Мэтьюза. Справа: Деталь хвоста распределения при T ₀ .

Условия N ( d ₁ ) и N ( d ₂ ) применяются при вычислении формулы Блэка-Шоулза и представляют собой выражения, связанные с операциями над логнормальными распределениями; см. раздел «Интерпретация» Блэка – Шоулза . Ссылаясь на рис. 5 и используя логарифмически нормальную форму опциона DM, можно получить определенное представление о внутренней работе опциона:

$N\left(\sigma -Z\right)=N\left(d_{1}\right)$

$N\left(-Z\right)=N\left(d_{2}\right)$

N ( -Z ) или N ( d ₂ ) является мерой площади хвоста распределения MT ) по отношению к (обозначенной X ₀ площади всего распределения, например вероятность хвоста распределения при время Т ₀ . Рис. 5, справа. Истинная вероятность истечения срока действия в деньгах в реальном («физическом») мире рассчитывается в момент времени T ₀ , даты запуска или страйка, измеряемой площадью хвоста распределения. N ( σ-Z ) или N ( d ₁ ) — это стоимость выигрыша по опциону относительно стоимости актива. $N(d_{1})=\left[MT\ x\ N(d_{2})\right]/S_{0},$ где MT — среднее значение хвоста в момент времени T ₀ .

Шаблоны данных

Упрощенное вычисление метода DM соответствует тем же основным характеристикам — это дисконтированное условное ожидание дисконтированного прогнозируемого распределения результатов будущей стоимости, или $MT$, за вычетом стоимости со скидкой, $X_{0}$, умноженный на вероятность выполнения, $N\left(-Z\right).$ Значение опции «Метод DM» можно понимать как $C_{0}=\left(MT-X_{0}\right)\ x\ N\left(-Z\right).$ Эта упрощенная формулировка имеет сильные параллели с расчетом ожидаемой стоимости .

Компании, которые собирают исторические данные, могут использовать сходство допущений в связанных проектах, облегчая расчет стоимости опционов. Одним из результирующих упрощений является коэффициент неопределенности , $\textstyle UR=(SD/S)$, который часто можно смоделировать как константу для аналогичных проектов. UR — это степень уверенности, с которой можно оценить прогнозируемые будущие денежные потоки. UR инвариант времени $\textstyle \left({\tfrac {SD_{T}}{S_{T}}}={\tfrac {SD_{0}}{S_{0}}}\right)$ со значениями обычно от 0,35 до 1,0 для многих многолетних бизнес-проектов.

Применение этого наблюдения в качестве константы K к приведенным выше формулам приводит к более простой формулировке:

${\text{Define }}K=\sigma ={\sqrt {\left[\ln(1+UR^{2})\right]}}{\text{, and }}\mu =\ln S_{0}-0.5\sigma ^{2}=\ln S_{0}-0.5K^{2}.$

$Z={\frac {(\ln X_{0}-\mu )}{\sigma }}={\tfrac {\ln \left({\tfrac {X_{0}}{S_{0}}}\right)}{K}}+0.5K{\text{, and }}-Z={\tfrac {\ln \left({\tfrac {S_{0}}{X_{0}}}\right)}{K}}-0.5K.$

$Z$ нормально распределяется, и доступ к значениям можно получить в таблице стандартных нормальных переменных . Результирующую реальную стоимость опциона можно просто рассчитать на ручном калькуляторе после определения K:

$C_{0}=S_{0}N\left(\sigma -Z\right)-X_{0}N\left(-Z\right)=S_{0}N\left(K-Z\right)-X_{0}N\left(-Z\right).$

Треугольная форма (опция диапазона)

Учитывая сложность оценки среднего логарифмически нормального распределения и стандартного отклонения будущих доходов, вместо этого для реальных опционов, используемых при принятии бизнес-решений, чаще применяются другие распределения. Выборочные , распределения могут принимать любую форму, хотя треугольное распределение часто используется , что типично для ситуаций с небольшим объемом данных за которым следует равномерное распределение (непрерывное) или бета-распределение . Этот подход полезен для оценки стоимости вариантов проекта на ранних стадиях, когда не было достаточно времени или ресурсов для сбора необходимой количественной информации, необходимой для полного моделирования денежных потоков, или в портфеле проектов, когда моделирование всех проектов слишком сложно. вычислительно требовательна. Независимо от выбранного распределения, процедура остается той же самой для реальной оценки опциона.

Рис. 6 Треугольное условное распределение вероятностей

Быстрая оценка условной стоимости инновационного проекта

При наиболее вероятном денежном потоке от солнечной операционной деятельности в размере 8,5 млн долларов США, но трехлетних капитальных затратах примерно в 20 млн долларов США, NPV важного инновационного проекта была глубоко отрицательной, и менеджер рассматривает возможность отказа от него. Аналитики корпоративных продаж подсчитали с вероятностью 95% (двусторонний шанс 1 из 10), что доходы могут составить от 4 миллионов долларов до 34 миллионов долларов. (Рис. 7) Из-за большого потенциального потенциала роста менеджер полагает, что небольшие первоначальные инвестиции могут устранить негативные факторы неопределенности проекта и раскрыть его потенциальную ценность. Рис. 7. Вариант диапазона DM с треугольным распределением. (Предпосылка: сопоставимое логнормальное распределение.) Используя в качестве ориентира вариант диапазона DM, менеджер рассчитал ожидаемую условную стоимость потенциала роста проекта примерно в 25 миллионов долларов США [≈ (2*20 миллионов долларов + 34 миллиона долларов США)/3]. Кроме того, существует вероятность одного из четырех {25% ≈ (34–20 миллионов долларов США). 2 /[ ($34 млн - $4 млн)($34 млн - $8,5 млн)]} что доходы проекта превысят 20 млн долларов США. С помощью этих расчетов менеджер оценивает стоимость варианта инновационного проекта в 1,25 млн долларов США [= (25–20 млн долларов США) * 25%]. Используя это значение, менеджер обосновывает первоначальные инвестиции (около 6% капитальных затрат) в проект, достаточные для устранения некоторых ключевых неопределенностей. Если промежуточные результаты разработки не оправдают себя, от проекта всегда можно отказаться, но инвестиционные потери будут минимизированы. (Позже, используя шаблоны корпоративных исторических данных, аналитик преобразовал значения из трехточечной оценки в расчет DM Option и продемонстрировал, что результат будет отличаться менее чем на 10%).

Для треугольного распределения, иногда называемого трехточечной оценкой , значение моды соответствует «наиболее вероятному» сценарию, а два других сценария, «пессимистический» и «оптимистический», представляют собой правдоподобные отклонения от наиболее вероятного сценария. сценарий (часто моделируемый как приближенный к двусторонней вероятности 1 из 10 или доверительной вероятности 95%). Этот диапазон оценок приводит к одноименному названию опциона — DM Range Option. Метод опционов диапазона DM аналогичен нечеткому методу для реальных опционов . В следующем примере (рис. 6) используется диапазон будущих предполагаемых операционных прибылей a (пессимистичный), b (оптимистичный) и m (режим или наиболее вероятный).

Для $T_{0}$ скидки a , b и m на $e^{-RT}{\text{ and }}X_{0}=X_{T}e^{-rT}.$

Классический метод DM предполагает, что цена исполнения представлена ​​случайной величиной (распределение ${\tilde {X}}_{0}$) с вариантным решением, полученным путем моделирования . В качестве альтернативы, без бремени моделирования, можно применить среднее или среднее скалярное значение распределения стоимости запуска. ${\bar {X}}_{0}$ (цена исполнения) дает консервативную оценку стоимости опциона диапазона DM. Если стоимость запуска заранее определена как скалярная величина, то расчет значения опции диапазона DM является точным.

Ожидаемое значение усеченного треугольного распределения (среднее значение правого хвоста) равно $MT={\tfrac {\left(2X_{0}+b\right)}{3}}.$

Вероятность того, что проект окупится и будет запущен, равна площади усеченного распределения относительно полного треугольного распределения. (См. рис. 16) Это частичное математическое ожидание вычисляется с помощью кумулятивной функции распределения (CDF), учитывая, что распределение вероятностей будет найдено при значении, большем или равном X :

$P(X_{0}|X_{0}\geq x)={\frac {\left(b-X_{0}\right)^{2}}{\left[\left(b-a\right)\left(b-m\right)\right]}}.$

Стоимость опциона DM Range, или инвестиции в проект, составляет:

$C_{0}=\left(MT-X_{0}\right)\cdot P\left(X_{0}\vert X_{0}\geq x\right)=\left(MT-X_{0}\right)\cdot \left\{{\frac {\left(b-X_{0}\right)^{2}}{\left[\left(b-a\right)\left(b-m\right)\right]}}\right\}.$

${\text{Note: }}\mu =0.5*\ln(a+b){\text{, }}\sigma =0.25*\ln(b/a){\text{, and }}UR={\sqrt {e^{\sigma ^{2}}-1}}.$

Использование опциона DM Range облегчает применение реальной оценки опциона к будущим инвестициям в проект. Опция DM Range обеспечивает оценку оценки, которая незначительно отличается от оценки алгебраической логнормальной формы распределения DM Option. Однако прогнозируемая будущая стоимость S проекта редко основывается на логарифмически нормальном распределении, полученном на основе исторической доходности активов, как это происходит с финансовым опционом. Скорее, будущая стоимость S (а также цена исполнения X и стандартное отклонение SD ) более чем вероятна трехбалльная оценка, основанная на инженерных и маркетинговых параметрах. Поэтому простота применения опции DM Range зачастую оправдана ее целесообразностью и достаточна для оценки условной стоимости будущего проекта.

Многоступенчатый (составной) вариант

Тимоти Луерман в статье HBR утверждает: «С финансовой точки зрения бизнес-стратегия больше похожа на серию вариантов, чем на серию статических денежных потоков или даже деревьев решений . Реализация стратегии почти всегда предполагает принятие последовательности рискованных решений». Многоэтапную оценку бизнес-стратегии можно смоделировать как последовательность поэтапных условных инвестиционных решений, структурированных как серия одноэтапных вариантов DM.

Рис. 8 Трехступенчатое распределение стоимости опциона.

При оценке сложной стратегической возможности, многоэтапного или составного варианта , — это более точный, но более математически требовательный подход, чем более простые вычисления с использованием модели дерева решений , диаграмм влияния или решетчатой ​​/ биномиальной модели. подходов Каждый этап зависит от выполнения или отказа (прибыль/успех или проигрыш/неуспех) последующего этапа с учетом инвестиционных затрат предыдущих этапов. В литературе упоминается несколько подходов к моделированию многоэтапного варианта. Трехэтапный вариант (1 проверка концепции, 2 разработка прототипа, 3 запуск/производство) можно смоделировать следующим образом: ${\begin{alignedat}{2}C_{0}=E{\Bigl (}&if\langle \left({\tilde {S}}_{1}e^{-Rt_{0}}\geq {\tilde {X}}_{1}e^{-rt_{0}}\right),if\lbrace \left({\tilde {S}}_{2}e^{-Rt_{0}}\geq {\tilde {X}}_{2}e^{-rt_{0}}+{\tilde {X}}_{1}e^{-rt_{0}}\right),\\&\left[max\left({\tilde {S}}_{3}e^{-Rt_{0}}-{\tilde {X}}_{3}e^{-rt_{0}},0\right)-{\tilde {X}}_{2}e^{-rt_{0}}-{\tilde {X}}_{1}e^{-rt_{0}}\right],-{\tilde {X}}_{1}e^{-rt_{0}}\rbrace ,0\rangle {\Bigr )}.\end{alignedat}}$

Затем оценка происходит в обратном порядке в зависимости от успеха или неудачи на каждом этапе. Номинальная стоимость этого трехэтапного варианта представляет собой среднее значение нескольких (обычно нескольких тысяч k испытаний) смоделированных денежных потоков.

Рис. 9. Зависимость пути для выбора кандидатов P*.

Хотя оценка многоэтапного варианта представляет технический интерес, основной задачей менеджера проекта является максимизация вероятности успеха и общей ценности проекта. Тщательный выбор этапов этапов проекта может одновременно достичь этих целей и обеспечить ясность управления проектом. Заданные точки контрольных точек определяются путем указания выигрыша по варианту для распределения значений конечного этапа n и обратного прогнозирования . предполагаемые вехи или пороговые значения стоимости для каждого этапа i . Обозначены $P_{i}^{*}$ (произносится как «П-звезда»). Множественные моделируемые денежные потоки, прогнозируемые на основе ${\tilde {S}}_{0}$, создайте шаблон ответов о стоимости опционов для каждого этапа, раскрывающий вехи потенциальных кандидатов. Моделирование оценивает значения вариантов выплаты. $E\lbrace \left[max\left({\tilde {S}}_{i}e^{-Rt_{0}}-{\tilde {X}}_{i}e^{-rt_{0}},0\right)-{\tilde {X}}_{i-1}e^{-rt_{0}}\right]\geq P_{i}^{*}\rbrace .$ Моделирование тысяч испытаний приводит к оценке и ранжированию больших наборов пар данных для каждого этапа i: этапа i сопоставляются с кандидатом значения вариантов $P_{i}^{*}$ ценности.

Рис. 10 Диапазон предполагаемых этапов; оптимальный P** в вершине.

Параболическое вариантами распределение пар точек данных отображает отсортированный диапазон . значений вариантов на этапе i в сравнении с перспективными $P_{i}^{*}$ Значения вех. Если выбрано $P_{i}^{*}$ установлен слишком низкий порог, наблюдаются чрезмерные отказы от упражнений, $\left({\tilde {S}}_{i}e^{-Rt_{0}}<P_{i}^{*}\right)$, и численно ожидаемая стоимость опциона уменьшается. Альтернативно, если выбрано $P_{i}^{*}$ порог установлен слишком высоким, тогда количество успешных упражнений будет недостаточным, и ожидаемая стоимость опциона снова уменьшится в численном отношении. Оптимальный этап $P_{i}^{**}$ Значение («P-двойная звезда»), возникающее в ходе моделирования, максимизирует общую стоимость варианта проекта за счет баланса прибылей и потерь.

Рис. 11. Стоимость эмерджентного опциона, определенная с помощью кандидатов P**.

Трехэтапный вариант, оптимизированный для управления по этапам и максимизации стоимости, можно смоделировать следующим образом:

${\begin{alignedat}{2}C_{0}=E{\Bigl (}&if\langle \left({\tilde {S}}_{1}e^{-Rt_{0}}\geq P_{1}^{**}\right),if\lbrace \left({\tilde {S}}_{2}e^{-Rt_{0}}\geq P_{2}^{**}\right),\\&\left[max\left({\tilde {S}}_{3}e^{-Rt_{0}}-{\tilde {X}}_{3}e^{-rt_{0}},0\right)-{\tilde {X}}_{2}e^{-rt_{0}}-{\tilde {X}}_{1}e^{-rt_{0}}\right],-{\tilde {X}}_{1}e^{-rt_{0}}\rbrace ,0\rangle {\Bigr )}.\end{alignedat}}$

Или, вкратце,

$C_{0}=E\left[max\left({\tilde {S}}_{n}e^{-Rt_{0}}-{\tilde {X}}_{n}e^{-rt_{0}},0\right)-{\tilde {X}}_{n-i}e^{-rt_{0}}\right]\times \mathbb {P} \left({\tilde {S}}_{1}^{n-1}e^{-Rt_{0}}\geq P_{1}^{n-1**}\right).$

Обратите внимание, что обычно $P_{i}^{**}\gg {\tilde {X}}_{i}e^{-rt_{0}}.$ Введение этих тщательно определенных условных этапов увеличивает общую ценность номинального многоэтапного опциона, поскольку каждый последующий этап был оптимизирован для максимизации стоимости опциона. Используя выбранные этапы, руководитель проекта достигает целей повышения вероятности успеха и общей ценности проекта, а также снижения бремени управления проектом.

Интеграция кривой спроса

Рис. 12. Кривые цены спроса и издержек. Точки максимальной доходности обозначены треугольными маркерами.

Многие проекты на ранних стадиях обнаруживают, что доминирующими неизвестными значениями являются оценки диапазона первого порядка основных компонентов операционной прибыли: выручки и себестоимости проданных товаров (COGS). В свою очередь, неопределенность в отношении доходов обусловлена ​​предположениями либо о цене рыночного спроса, либо о размере. Рыночную цену и размер можно оценить независимо, хотя от рыночного спроса лучшим подходом является объединение их вместе в зависимости . COGS, общая стоимость количества продукции, подлежащей продаже, является конечным компонентом и тенденцией в соответствии с зависимостью затрат от кривой опыта или обучения, связанной с размером рынка. Взаимодействие этих трех рыночных элементов в рамках моделирования реальных опционов DM, даже с диапазонами на ранних стадиях, может снизить неопределенность при планировании проекта, давая разумно суженные целевые оценки цен на продукт и размера производства, что максимизирует потенциальную операционную прибыль и повышает стоимость опциона.

Рис. 13 Слева: высокодифференцированный рынок авиабилетов (MCO -- SFO), показывающий суммы тарифов, уплачиваемые пассажирами (PAX). Справа: кумулятивное упорядочение данных по Парето, иллюстрирующее соответствие обратной логарифмически нормальной кривой спроса.

Рис. 14. Единичный пример (моделирование) трех компонентов, формирующих график операционной прибыли. Треугольные маркеры указывают максимальное значение операционной прибыли, очерчивая оптимальную цену, единицы продукции и значения затрат. Желтые строки указывают оптимальные диапазоны.

на рыночную цену Кривая спроса отображает зависимость цены от размера или требуемого количества. Закон спроса гласит, что существует обратная зависимость между ценой и объемом спроса, или просто по мере снижения цены спрос на продукцию будет увеличиваться. Вторая кривая, график производственных затрат, моделирует эффект кривой обучения, иллюстрируя взаимосвязь между количеством произведенных товаров и повышением эффективности этого производства. Рис. 12. Математически кривая обучения имеет вид степенной функции.

Кривую спроса можно реалистично смоделировать с использованием обратного логарифмически нормального распределения, которое сверяет оценку распределения рыночных цен с диапазоном размеров рынка. Кривая спроса умело моделирует высокодифференцированные рынки , которые посредством ценообразования различают отдельные характеристики продукта или услуги, такие как качество или сорт, функциональные особенности и доступность, а также проданное количество. Примерами являются автомобили, обувь, смартфоны и компьютеры. Рынки авиабилетов сильно дифференцированы, где цены спроса и продаваемое количество зависят от сезонности, дня недели, времени суток, маршрута, рекламных акций, а также места или класса тарифа. Распределение спроса на авиабилеты хорошо представлено обратным логнормальным распределением, как показано на рис. 13.

Кривые для всех вышеперечисленных компонентов, рыночной цены, размера и себестоимости, можно смоделировать с возможностью изменения, чтобы получить оптимальные входные данные операционной прибыли для расчета реального опциона (рис. 14). Например, результаты моделирования, представленные на рис. 15, указывают диапазоны цен и количества единиц продукции, которые потенциально позволят максимизировать прибыльность. Выбор пиковых (частотных) значений, извлеченных из этих оценок диапазона первого порядка, определяет значительно суженный разброс многообещающих оценок. Знание этих оптимальных разбросов стоимости существенно снижает неопределенность и обеспечивает лучший, более целенаправленный набор параметров, на основе которых можно уверенно основывать планы инновационного развития и стоимость опционов.

Рис. 15 Оптимальные диапазоны для максимизации прибыльности. Слева: цена 56–62 тыс. долларов. Справа: единицы 120–150 тыс. Результат: оценка улучшена на 85%+.

Сравнение с другими методами

Метод нечеткой выплаты для оценки реальных опционов , созданный в 2009 году, обеспечивает еще один доступный подход к оценке реальных опционов. Хотя каждый из них использует разные математические методы (Fuzzy: нечеткая логика ; DM: численное моделирование и геометрия), основной принцип поразительно схож: вероятность положительного выигрыша. Отдельное рассмотрение двух факторов (возможности/вероятности и положительного выигрыша) демонстрирует это сходство.

Рис. 16 Соотношение площадей пропорционально вероятности.

Функция возможности нечеткого выигрыша равна ${\tfrac {A(Pos)}{A(Pos)+A(Neg)}}$. Простая интерпретация — это пропорциональности отношение положительной площади нечеткой чистой приведенной стоимости к общей площади нечеткой чистой приведенной стоимости. Вероятность выигрыша проекта для варианта диапазона DM пропорциональна площади (CDF) положительного распределения относительно полного распределения. Это вычисляется как ${\tfrac {\left(b-X_{0}\right)^{2}}{\left[\left(b-a\right)\left(b-m\right)\right]}}.$ В каждом случае соотношения площадей рассчитываются для одного и того же значения возможности/вероятности. Положительный выигрыш нечеткой выплаты просто является средним значением положительной области нечеткой чистой приведенной стоимости, или $E[A^{+}]$. Аналогично, положительный выигрыш для опции диапазона DM — это среднее значение правого хвоста ( MT ), или ${\tfrac {\left(2X_{0}+b\right)}{3}}$ меньше страйк-цены $X_{0}$ Это понимание механики двух методов иллюстрирует не только их сходство, но и их эквивалентность.

В статье 2016 года, опубликованной в журнале Advances in Decision Sciences , исследователи из Школы бизнеса и менеджмента Технологического университета Лаппеенранты сравнили метод DM с методом нечетких выплат для оценки реальных опционов и отметили, что, хотя результаты оценки были схожими, метод нечеткой выплаты был более устойчивым в некоторых условиях. В некоторых сравнительных случаях метод Датара-Мэтьюза имеет значительное преимущество, заключающееся в том, что с ним проще работать, и он связывает оценку чистой приведенной стоимости и анализ сценариев с методом моделирования (или геометрии) Монте-Карло, что значительно улучшает интуицию при использовании методов реальных опционов в управленческой деятельности. решение и объяснение третьим лицам. Благодаря интерфейсу моделирования метод Датара-Мэтьюза легко учитывает несколько, а иногда и коррелированные сценарии движения денежных средств, включая динамическое программирование, типичное для сложных проектов, таких как аэрокосмическая отрасль, которые трудно моделировать с использованием нечетких множеств.

Метод DM и теория перспектив

Реальные варианты – это объективная оценка инновационных возможностей. К сожалению, эти возможности, мимолетные и, казалось бы, рискованные, часто воспринимаются субъективно. Однако как объективный механизм оценки, так и субъективная интерпретация результатов часто понимаются неправильно, что приводит к нежеланию инвестировать и потенциально недооценивать возможности.

Реальный опцион DM использует формулу объективной оценки. $C_{0}=E[\max(...,{\color {red}0)}],$ где $\color {red}0$ — это порог по умолчанию, когда экономически целесообразно прекратить (отказаться от) возможного события. Если событие моделирования («ничья») рассчитывает отрицательный результат (т. е. $[{\tilde {S}}_{T}e^{-Rt}\leq {\tilde {X}}_{T}e^{-rt}],$ операционная прибыль меньше затрат на запуск), то результат этого события следует рационально сократить или прекратить, зафиксировав $\color {red}0$ остаток. Только чистые положительные экономические результаты $[{\tilde {S}}_{T}e^{-Rt}>{\tilde {X}}_{T}e^{-rt}]$ подсчитываются. Эта операция оставляет неправильное представление о том, что «шансы складываются», отдавая предпочтение только положительным результатам, что, по-видимому, приводит к аномально высокой оценке. Однако $E$ формулы $C_{0}=E[\max(...,0)]$ математически вычисляет правильную стоимость варианта, корректируя эти положительные результаты в соответствии с их вероятностью, т. е. вероятностью успеха (POS).

Фактическая формула DM: $C_{0}=E[\max(...,{\color {red}?})],$ где порог $\color {red}?$ («минимальный уровень») может принимать любое значение (или альтернативную формулу), включая значение по умолчанию. $\color {red}0$. Использование порога, отличного от $\color {red}0$ преобразует формулу в вариант варианта, взвешенного по барьерам. Результат больше не эквивалентен стоимости финансового опциона.

Рис. 17. Результаты с низкой вероятностью и высокой ценностью (красный кружок).

Большая часть воспринимаемой высокой ценности реальной оценки опциона непропорционально расположена в крайнем правом конце хвоста распределения моделирования, в области низкой вероятности, но высокой ценности результатов. Оценка опциона отражает потенциальную ценность возможности, если различные предположения о результате подтвердятся. Целевые дополнительные инвестиции могут подтвердить эти маловероятные предположения. Если нет, замените предположения проверенными «правдоподобными» элементами, а затем пересчитайте значение на основе новых знаний.

Субъективную недооценку реальных возможностей частично можно объяснить поведенческими науками . Инновационный инвестор может воспринимать первоначальные инвестиции как потенциально убыточные, особенно если POS низкий. Канемана и Тверски Теория перспектив утверждает, что потери воспринимаются более чем в два раза сильнее, чем выигрыши на ту же стоимость. В результате инвестор , не склонный к потерям, субъективно недооценивает возможность и, следовательно, инвестиции, несмотря на объективную и финансово точную оценку реального опциона.

Неприятие сожаления , еще одно наблюдение поведенческой науки, возникает, когда принимается необоснованное решение, чтобы не сожалеть о будущем результате. Например, инвестор, не склонный к сожалениям, решает инвестировать в относительно «верную ставку», но с меньшим выигрышем по сравнению с альтернативой со значительно более высоким, но предположительно неопределенным выигрышем. Феномен неприятия сожалений тесно связан с неприятием неопределенности (предвзятостью уверенности), когда неизвестные аспекты инновационных возможностей (т. е. новизна, отсутствие контроля) рационализируются как препятствие для дальнейших инвестиций. Последствиями принятия решений, не допускающих потерь и сожалений, являются скудные инвестиции и недостаточное финансирование («недооценка») многообещающих инновационных возможностей на ранних стадиях.

Сообразительный инвестор может преодолеть ошибочную оценку цены опциона. Неприятие потерь значительно возрастает, когда вся стоимость опциона интерпретируется как инвестиционный риск. Эта эмоциональная реакция не учитывает, что первоначальные инвестиции на ранней стадии составляют лишь часть всей стоимости опциона и обязательно направлены на подтверждение наиболее важных предположений. Точно так же неприятие сожалений не следует ошибочно воспринимать как неприятие риска, поскольку риск небольших инвестиций на ранней стадии обычно не является существенным. Вместо этого эти первоначальные инвестиции тщательно исследуют основную ценность возможности, одновременно обеспечивая ощущение контроля над неопределенным в противном случае результатом. Сожаление сводится к минимуму за счет осознания того, что развитие возможностей может быть прекращено, если результаты предположений не являются многообещающими. Затрачиваемые инвестиционные средства разумно используются только для исследования многообещающей возможности и, в свою очередь, увеличиваются за счет приобретенных знаний.

Поскольку люди склонны к когнитивным искажениям , для их уменьшения разрабатываются различные стратегии вмешательства, включая экспертную оценку, а также предвзятость и понимание наивного реализма . Феномен, называемый « слепое пятно предубеждений », кратко описывает бессознательную восприимчивость человека к предубеждениям. Эта фундаментальная ошибка атрибуции остается подсознательно скрытой иллюзией самоанализа , то есть ложной верой в то, что у нас есть доступ к нашим внутренним намерениям или мотивациям. Предубеждения могут быть рационализированы постфактум, но, тем не менее, они влияют на процесс принятия решений. Чтобы противодействовать предубеждениям, недостаточно просто знать их характеристики, необходимо также научиться осознавать собственные иллюзии самоанализа.