Логнормальное распределение

Логнормальное распределение

Функция плотности вероятности Идентичный параметр $\ \mu \$ но разные параметры $\sigma$
Кумулятивная функция распределения $\ \mu =0\$
Обозначения	$\ \operatorname {Lognormal} \left(\ \mu ,\,\sigma ^{2}\ \right)\$
Параметры	$\ \mu \in (\ -\infty ,+\infty \ )\$ (логарифм местоположения ), $\ \sigma >0\$ (логарифм масштаба )
Поддерживать	$\ x\in (\ 0,+\infty \ )\$
PDF	$\ {\frac {1}{\ x\sigma {\sqrt {2\pi \ }}\ }}\ \exp \left(-{\frac {\left(\ln x-\mu \ \right)^{2}}{2\sigma ^{2}}}\right)$
CDF	$\ {\frac {\ 1\ }{2}}\left[1+\operatorname {erf} \left({\frac {\ \ln x-\mu \ }{\sigma {\sqrt {2\ }}}}\right)\right]=\Phi \left({\frac {\ln(x)-\mu }{\sigma }}\right)$
Квантиль	$\ \exp \left(\mu +{\sqrt {2\sigma ^{2}}}\operatorname {erf} ^{-1}(2p-1)\right)\$
Иметь в виду	$\ \exp \left(\ \mu +{\frac {\sigma ^{2}}{2}}\ \right)\$
медиана	$\ \exp(\ \mu \ )\$
Режим	$\ \exp \left(\ \mu -\sigma ^{2}\ \right)\$
Дисперсия	$\ \left[\ \exp(\sigma ^{2})-1\ \right]\ \exp \left(2\ \mu +\sigma ^{2}\right)\$
асимметрия	$\ \left[\ \exp \left(\sigma ^{2}\right)+2\ \right]{\sqrt {\exp(\sigma ^{2})-1\;}}$
Избыточный эксцесс	$\ 1\ \exp \left(4\ \sigma ^{2}\right)+2\ \exp \left(3\ \sigma ^{2}\right)+3\ \exp \left(2\sigma ^{2}\right)-6\$
Энтропия	$\ \log _{2}\left(\ {\sqrt {2\pi \ }}\ \sigma \ e^{\mu +{\tfrac {1}{2}}}\ \right)\$
МГФ	определено только для чисел с неположительная действительная часть, см. текст
CF	представительство $\ \sum _{n=0}^{\infty }{\frac {\ (i\ t)^{n}\ }{n!}}e^{\ n\mu +n^{2}\sigma ^{2}/2}\$ асимптотически расходится, но достаточен для большинства числовых целей
Информация о Фишере	$\ {\begin{pmatrix}{\frac {1}{\ \sigma ^{2}\ }}&0\\0&{\frac {2}{\ \sigma ^{2}\ }}\end{pmatrix}}\$
Метод моментов	$\ \mu =\log \left({\frac {\operatorname {\mathbb {E} } [X]\ }{\ {\sqrt {{\frac {\ \operatorname {Var} [X]~~}{\ \operatorname {\mathbb {E} } [X]^{2}\ }}+1\ }}\ }}\right)\ ,$ $\ \sigma ={\sqrt {\log \left({\frac {\ \operatorname {Var} [X]~~}{\ \operatorname {\mathbb {E} } [X]^{2}\ }}+1\ \right)\ }}$
Ожидаемый дефицит	$\ {\frac {\ \operatorname {erfc} \left({\frac {s}{\ {\sqrt {2\ }}\ }}-\operatorname {erf} ^{-1}(2p-1)\right)\ }{2}}(1-p)e^{\mu +{\frac {~s^{2}\ }{2}}}\$

В теории вероятностей распределение логнормальное (или логнормальное ) — это непрерывное распределение вероятностей случайной величины которой , логарифм нормально распределен . Таким образом, если случайная величина X имеет логнормальное распределение, то Y = ln( X ) имеет нормальное распределение. Эквивалентно, если = exp ( Y , ) Y имеет нормальное распределение, то показательная функция Y , X имеет логарифмически нормальное распределение . Случайная величина, имеющая логнормальное распределение, принимает только положительные действительные значения. Это удобная и полезная модель для измерений в естественных науках , технике , а также медицине , экономике и других областях. Его можно применять к различным величинам, таким как энергия, концентрация, длина, цены финансовых инструментов и другие показатели, признавая при этом присущую всем измерениям неопределенность.

Распределение иногда называют распределением Гальтона или распределением Гальтона в честь Фрэнсиса Гальтона . Логнормальное распределение также ассоциировалось с другими именами, такими как Макалистер , Гибрат и Кобб-Дуглас .

Логнормальный процесс — это статистическая реализация мультипликативного произведения многих независимых случайных величин , каждая из которых положительна. Это подтверждается рассмотрением центральной предельной теоремы в логарифмической области (иногда называемой законом Гибрата ). Логарифмически нормальное распределение — это распределение вероятностей максимальной энтропии для случайной величины X среднее значение и дисперсия ln( X ) . , для которого указаны

Определения

Генерация и параметры

Позволять $\ Z\$ — стандартная нормальная переменная , и пусть $\mu$ и $\sigma$ быть двумя действительными числами, причем $\sigma >0$. Тогда распределение случайной величины

$X=e^{\mu +\sigma Z}$

называется логнормальным распределением с параметрами $\mu$ и $\sigma$. Это ожидаемое значение (или среднее значение ) и стандартное отклонение переменной натурального логарифма , а не математическое ожидание и стандартное отклонение $\ X\$ сам.

Связь между нормальным и логнормальным распределением. Если $\ Y=\mu +\sigma Z\$ нормально распределено, то $\ X\sim e^{Y}\$ имеет логнормальное распределение.

Это соотношение верно независимо от основания логарифмической или показательной функции: Если $\ \log _{a}(X)\$ нормально распределено, то и так $\ \log _{b}(X)\$ для любых двух положительных чисел $\ a,b\neq 1~.$ Аналогично, если $\ e^{Y}\$ распределено логнормально, то так же $\ a^{Y}\ ,$ где $0<a\neq 1$.

Чтобы получить распределение с желаемым средним значением $\mu _{X}$ и дисперсия $\ \sigma _{X}^{2}\ ,$ человек использует $\ \mu =\ln \left({\frac {\mu _{X}^{2}}{\ {\sqrt {\mu _{X}^{2}+\sigma _{X}^{2}\ }}\ }}\right)\$ и $\ \sigma ^{2}=\ln \left(1+{\frac {\ \sigma _{X}^{2}\ }{\mu _{X}^{2}}}\right)~.$

Альтернативно, «мультипликативные» или «геометрические» параметры $\ \mu ^{*}=e^{\mu }\$ и $\ \sigma ^{*}=e^{\sigma }\$ можно использовать. Они имеют более прямое толкование: $\ \mu ^{*}\$ является медианой распределения, и $\ \sigma ^{*}\$ полезен для определения интервалов «разброса», см. ниже.

Функция плотности вероятности

Положительная случайная величина $\ X\$ имеет логнормальное распределение (т.е. $\ X\sim \operatorname {Lognormal} \left(\ \mu ,\sigma ^{2}\ \right)\$), если натуральный логарифм $\ X\$ обычно распределяется со средним значением $\mu$ и дисперсия $\ \sigma ^{2}\ :$

$\ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})$

Позволять $\ \Phi \$ и $\ \varphi \$ быть соответственно кумулятивной функцией распределения вероятностей и функцией плотности вероятности $\ {\mathcal {N}}(\ 0,1\ )\$ стандартное нормальное распределение, то мы имеем это функция плотности вероятности логарифмически нормального распределения определяется выражением:

$${\begin{aligned}f_{X}(x)&={\frac {\rm {d}}{{\rm {d}}x}}\ \operatorname {\mathbb {P} _{\mathit {X}}} \,\!{\bigl [}\ X\leq x\ {\bigr ]}\\[6pt]&={\frac {\rm {d}}{{\rm {d}}x}}\ \operatorname {\mathbb {P} _{\mathit {X}}} \,\!{\bigl [}\ \ln X\leq \ln x\ {\bigr ]}\\[6pt]&={\frac {\rm {d}}{{\rm {d}}x}}\operatorname {\Phi } \!\!\left({\frac {\ \ln x-\mu \ }{\sigma }}\right)\\[6pt]&=\operatorname {\varphi } \!\left({\frac {\ln x-\mu }{\sigma }}\right){\frac {\rm {d}}{{\rm {d}}x}}\left({\frac {\ \ln x-\mu \ }{\sigma }}\right)\\[6pt]&=\operatorname {\varphi } \!\left({\frac {\ \ln x-\mu \ }{\sigma }}\right){\frac {1}{\ \sigma \ x\ }}\\[6pt]&={\frac {1}{\ x\ \sigma {\sqrt {2\ \pi \ }}\ }}\exp \left(-{\frac {\ (\ln x-\mu )^{2}\ }{2\ \sigma ^{2}}}\right)~.\end{aligned}}$$

Кумулятивная функция распределения

Кумулятивная функция распределения равна

$F_{X}(x)=\Phi \left({\frac {(\ln x)-\mu }{\sigma }}\right)$

где $\ \Phi \$ — кумулятивная функция распределения стандартного нормального распределения (т. е. $\ \operatorname {\mathcal {N}} (\ 0,\ 1)\$).

Это также может быть выражено следующим образом:

${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)$

где erfc — дополнительная функция ошибок .

Многомерный логарифмически нормальный

Если ${\boldsymbol {X}}\sim {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})$ является многомерным нормальным распределением , то $Y_{i}=\exp(X_{i})$ имеет многомерное логнормальное распределение. Экспонента применяется поэлементно к случайному вектору ${\boldsymbol {X}}$. Среднее значение ${\boldsymbol {Y}}$ является

$\operatorname {E} [{\boldsymbol {Y}}]_{i}=e^{\mu _{i}+{\frac {1}{2}}\Sigma _{ii}},$

и его ковариационная матрица равна

$\operatorname {Var} [{\boldsymbol {Y}}]_{ij}=e^{\mu _{i}+\mu _{j}+{\frac {1}{2}}(\Sigma _{ii}+\Sigma _{jj})}(e^{\Sigma _{ij}}-1).$

Поскольку многомерное логнормальное распределение широко не используется, остальная часть этой статьи посвящена только одномерному распределению .

Характеристическая функция и производящая функция момента

Все моменты логнормального распределения существуют и

$\operatorname {E} [X^{n}]=e^{n\mu +n^{2}\sigma ^{2}/2}$

Это можно получить, позволив $z={\tfrac {\ln(x)-(\mu +n\sigma ^{2})}{\sigma }}$ внутри интеграла. Однако логнормальное распределение не определяется своими моментами. Это означает, что он не может иметь определенную производящую функцию момента в окрестности нуля. Действительно, ожидаемое значение $\operatorname {E} [e^{tX}]$ не определено ни для одного положительного значения аргумента $t$, поскольку определяющий интеграл расходится.

Характеристическая функция $\operatorname {E} [e^{itX}]$ определяется для действительных значений t , но не определяется для любого комплексного значения t , имеющего отрицательную мнимую часть, и, следовательно, характеристическая функция не является аналитической в ​​начале координат. Следовательно, характеристическую функцию логнормального распределения нельзя представить в виде бесконечного сходящегося ряда. В частности, его формальный ряд Тейлора расходится:

$\sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}$

ряд альтернативных представлений расходящихся рядов . Однако был получен

Замкнутая формула для характеристической функции $\varphi (t)$ с $t$ в области сходимости неизвестно. Относительно простая аппроксимирующая формула доступна в закрытой форме и имеет вид

$\varphi (t)\approx {\frac {\exp \left(-{\frac {W^{2}(-it\sigma ^{2}e^{\mu })+2W(-it\sigma ^{2}e^{\mu })}{2\sigma ^{2}}}\right)}{\sqrt {1+W(-it\sigma ^{2}e^{\mu })}}}$

где $W$ — Ламберта W. функция Это приближение получено асимптотическим методом, но остается точным во всей области сходимости $\varphi$.

Характеристики

а. $y$ является логнормальной переменной с $\mu =1,\sigma =0.5$. $p(\sin y>0)$ вычисляется путем преобразования в нормальную переменную $x=\ln y$, затем интегрируя его плотность по области, определяемой формулой $\sin e^{x}>0$ (синие области), используя численный метод трассировки лучей. б и в. PDF и CDF функции $\sin y$ логарифмически нормальной переменной также можно вычислить таким способом.

Вероятность в разных областях

Вероятностное содержание логарифмически нормального распределения в любой произвольной области можно вычислить с желаемой точностью, сначала преобразуя переменную в нормальную, а затем численно интегрируя с использованием метода трассировки лучей. ( код Матлаба )

Вероятности функций логнормальной переменной

Поскольку вероятность логарифмически нормального значения может быть вычислена в любой области, это означает, что CDF (и, следовательно, PDF и обратный CDF) любой функции логнормальной переменной также можно вычислить. ( код Матлаба )

Геометрические или мультипликативные моменты

Среднее геометрическое или мультипликативное логарифмически нормального распределения равно $\operatorname {GM} [X]=e^{\mu }=\mu ^{*}$. Оно равно медиане. Геометрическое или мультипликативное стандартное отклонение равно $\operatorname {GSD} [X]=e^{\sigma }=\sigma ^{*}$.

По аналогии с арифметической статистикой можно определить геометрическую дисперсию: $\operatorname {GVar} [X]=e^{\sigma ^{2}}$, и геометрический коэффициент вариации , $\operatorname {GCV} [X]=e^{\sigma }-1$, было предложено. Этот термин был задуман как аналог коэффициента вариации для описания мультипликативной вариации логарифмически нормальных данных, но это определение GCV не имеет теоретической основы в качестве оценки $\operatorname {CV}$ сам по себе (см. также Коэффициент вариации ).

Обратите внимание, что среднее геометрическое меньше среднего арифметического. Это связано с неравенством AM – GM и является следствием того, что логарифм является вогнутой функцией . Фактически,

$\operatorname {E} [X]=e^{\mu +{\frac {1}{2}}\sigma ^{2}}=e^{\mu }\cdot {\sqrt {e^{\sigma ^{2}}}}=\operatorname {GM} [X]\cdot {\sqrt {\operatorname {GVar} [X]}}.$

В финансах термин $e^{-{\frac {1}{2}}\sigma ^{2}}$ иногда интерпретируется как коррекция выпуклости . С точки зрения стохастического исчисления , это тот же поправочный член, что и в лемме Ито для геометрического броуновского движения .

Арифметические моменты

любого действительного или комплексного числа n момент n -й Для логарифмически нормально распределенной переменной X определяется выражением

$\operatorname {E} [X^{n}]=e^{n\mu +{\frac {1}{2}}n^{2}\sigma ^{2}}.$

В частности, среднее арифметическое, ожидаемый квадрат, арифметическая дисперсия и стандартное арифметическое отклонение логарифмически нормально распределенной переменной X соответственно определяются выражением:

${\begin{aligned}\operatorname {E} [X]&=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}},\\[4pt]\operatorname {E} [X^{2}]&=e^{2\mu +2\sigma ^{2}},\\[4pt]\operatorname {Var} [X]&=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=(\operatorname {E} [X])^{2}(e^{\sigma ^{2}}-1)=e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1),\\[4pt]\operatorname {SD} [X]&={\sqrt {\operatorname {Var} [X]}}=\operatorname {E} [X]{\sqrt {e^{\sigma ^{2}}-1}}=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}}{\sqrt {e^{\sigma ^{2}}-1}},\end{aligned}}$

Арифметический коэффициент вариации $\operatorname {CV} [X]$ это соотношение ${\tfrac {\operatorname {SD} [X]}{\operatorname {E} [X]}}$. Для логнормального распределения оно равно

$\operatorname {CV} [X]={\sqrt {e^{\sigma ^{2}}-1}}.$

Эту оценку иногда называют «геометрическим CV» (GCV). из-за использования геометрической дисперсии. В отличие от стандартного арифметического отклонения, арифметический коэффициент вариации не зависит от среднего арифметического.

Параметры μ и σ можно получить, если известны среднее арифметическое и дисперсия:

${\begin{aligned}\mu &=\ln \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {E} [X^{2}]}}}\right)=\ln \left({\frac {\operatorname {E} [X]^{2}}{\sqrt {\operatorname {Var} [X]+\operatorname {E} [X]^{2}}}}\right),\\[4pt]\sigma ^{2}&=\ln \left({\frac {\operatorname {E} [X^{2}]}{\operatorname {E} [X]^{2}}}\right)=\ln \left(1+{\frac {\operatorname {Var} [X]}{\operatorname {E} [X]^{2}}}\right).\end{aligned}}$

Распределение вероятностей не определяется однозначно моментами E[ X ^н ] = и ^{nμ + ⁠ 1 / 2 ⁠ n 2 п 2} для n ≥ 1 . То есть существуют другие распределения с таким же набором моментов. На самом деле существует целое семейство распределений с теми же моментами, что и логнормальное распределение.

Мода, медиана, квантиль

Сравнение среднего значения , медианы и моды двух логнормальных распределений с различной асимметрией .

Мода является точкой глобального максимума функции плотности вероятности. В частности, решив уравнение $(\ln f)'=0$, мы получаем следующее:

$\operatorname {Mode} [X]=e^{\mu -\sigma ^{2}}.$

Поскольку логарифмически преобразованная переменная $Y=\ln X$ имеет нормальное распределение, а квантили сохраняются при монотонных преобразованиях, квантили $X$ являются

$q_{X}(\alpha )=e^{\mu +\sigma q_{\Phi }(\alpha )}=\mu ^{*}(\sigma ^{*})^{q_{\Phi }(\alpha )},$

где $q_{\Phi }(\alpha )$ — квантиль стандартного нормального распределения.

В частности, медиана логарифмически нормального распределения равна его мультипликативному среднему:

$\operatorname {Med} [X]=e^{\mu }=\mu ^{*}~.$

Частичное ожидание

Частичное ожидание случайной величины $X$ относительно порога $k$ определяется как

$g(k)=\int _{k}^{\infty }xf_{X}(x\mid X>k)\,dx.$

Альтернативно, используя определение условного ожидания , его можно записать как $g(k)=\operatorname {E} [X\mid X>k]P(X>k)$. Для логнормальной случайной величины частичное математическое ожидание определяется выражением:

$g(k)=\int _{k}^{\infty }xf_{X}(x\mid X>k)\,dx=e^{\mu +{\tfrac {1}{2}}\sigma ^{2}}\,\Phi \!\left({\frac {\mu +\sigma ^{2}-\ln k}{\sigma }}\right)$

где $\Phi$ – нормальная кумулятивная функция распределения . Вывод формулы представлен на странице Обсуждение . Формула частных ожиданий имеет приложения в страховании и экономике , она используется при решении уравнения в частных производных, приводящего к формуле Блэка-Шоулза .

Условное ожидание

Условное математическое ожидание логнормальной случайной величины $X$— относительно порога $k$- это его частичное ожидание, разделенное на кумулятивную вероятность попадания в этот диапазон:

${\begin{aligned}E[X\mid X<k]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\ln(k)-\mu -\sigma ^{2}}{\sigma }}\right]}{\Phi \left[{\frac {\ln(k)-\mu }{\sigma }}\right]}}\\[8pt]E[X\mid X\geqslant k]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\mu +\sigma ^{2}-\ln(k)}{\sigma }}\right]}{1-\Phi \left[{\frac {\ln(k)-\mu }{\sigma }}\right]}}\\[8pt]E[X\mid X\in [k_{1},k_{2}]]&=e^{\mu +{\frac {\sigma ^{2}}{2}}}\cdot {\frac {\Phi \left[{\frac {\ln(k_{2})-\mu -\sigma ^{2}}{\sigma }}\right]-\Phi \left[{\frac {\ln(k_{1})-\mu -\sigma ^{2}}{\sigma }}\right]}{\Phi \left[{\frac {\ln(k_{2})-\mu }{\sigma }}\right]-\Phi \left[{\frac {\ln(k_{1})-\mu }{\sigma }}\right]}}\end{aligned}}$

Альтернативные параметризации

Помимо характеристики по $\mu ,\sigma$ или $\mu ^{*},\sigma ^{*}$, вот несколько способов параметризации логарифмически нормального распределения. ProbOnto , база знаний и онтология вероятностных распределений перечисляет семь таких форм:

Обзор параметризации логнормальных распределений.

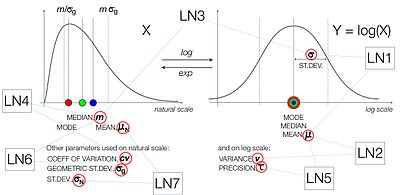
• LogNormal1(μ,σ) со средним значением µ и стандартным отклонением σ, оба в логарифмической шкале.

  $P(x;{\boldsymbol {\mu }},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left[-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right]$

• LogNormal2(μ,υ) со средним значением μ и дисперсией υ, оба в логарифмическом масштабе.

  $P(x;{\boldsymbol {\mu }},{\boldsymbol {v}})={\frac {1}{x{\sqrt {v}}{\sqrt {2\pi }}}}\exp \left[-{\frac {(\ln x-\mu )^{2}}{2v}}\right]$

• LogNormal3(m,σ) с медианой m в естественном масштабе и стандартным отклонением σ в логарифмическом масштабе.

  $P(x;{\boldsymbol {m}},{\boldsymbol {\sigma }})={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left[-{\frac {\ln ^{2}(x/m)}{2\sigma ^{2}}}\right]$

• LogNormal4(m,cv) с медианой m и коэффициентом вариации cv, оба в естественном масштабе.

  $P(x;{\boldsymbol {m}},{\boldsymbol {cv}})={\frac {1}{x{\sqrt {\ln(cv^{2}+1)}}{\sqrt {2\pi }}}}\exp \left[-{\frac {\ln ^{2}(x/m)}{2\ln(cv^{2}+1)}}\right]$

• LogNormal5(μ,τ) со средним значением μ и точностью τ, оба в логарифмическом масштабе.

  $P(x;{\boldsymbol {\mu }},{\boldsymbol {\tau }})={\sqrt {\frac {\tau }{2\pi }}}{\frac {1}{x}}\exp \left[-{\frac {\tau }{2}}(\ln x-\mu )^{2}\right]$

• LogNormal6(m,σg ₎ с медианой m и геометрическим стандартным отклонением σg _, оба в естественном масштабе.

  $P(x;{\boldsymbol {m}},{\boldsymbol {\sigma _{g}}})={\frac {1}{x\ln(\sigma _{g}){\sqrt {2\pi }}}}\exp \left[-{\frac {\ln ^{2}(x/m)}{2\ln ^{2}(\sigma _{g})}}\right]$

• LogNormal7(μ _N ,σ _N ) со средним значением μ _N и стандартным отклонением σ _N в естественной шкале.

  $P(x;{\boldsymbol {\mu _{N}}},{\boldsymbol {\sigma _{N}}})={\frac {1}{x{\sqrt {2\pi \ln \left(1+\sigma _{N}^{2}/\mu _{N}^{2}\right)}}}}\exp \left(-{\frac {{\Big [}\ln x-\ln {\frac {\mu _{N}}{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}}{\Big ]}^{2}}{2\ln(1+\sigma _{N}^{2}/\mu _{N}^{2})}}\right)$

Примеры повторной параметризации

Рассмотрим ситуацию, когда хотелось бы запустить модель с использованием двух разных оптимальных инструментов проектирования, например PFIM. и ПопЭД. Первый поддерживает параметризацию LN2, второй LN7 соответственно. Поэтому требуется повторная параметризация, иначе два инструмента дадут разные результаты.

Для перехода $\operatorname {LN2} (\mu ,v)\to \operatorname {LN7} (\mu _{N},\sigma _{N})$ следующие формулы имеют место ${\textstyle \mu _{N}=\exp(\mu +v/2)}$ и ${\textstyle \sigma _{N}=\exp(\mu +v/2){\sqrt {\exp(v)-1}}}$.

Для перехода $\operatorname {LN7} (\mu _{N},\sigma _{N})\to \operatorname {LN2} (\mu ,v)$ следующие формулы имеют место ${\textstyle \mu =\ln \left(\mu _{N}/{\sqrt {1+\sigma _{N}^{2}/\mu _{N}^{2}}}\right)}$ и ${\textstyle v=\ln(1+\sigma _{N}^{2}/\mu _{N}^{2})}$.

Все остальные формулы перепараметризации можно найти в спецификации на сайте проекта.

Множественная, взаимная, сила

• Умножение на константу: Если $X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$ затем $aX\sim \operatorname {Lognormal} (\mu +\ln a,\ \sigma ^{2})$ для $a>0.$
• Взаимное: если $X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$ затем ${\tfrac {1}{X}}\sim \operatorname {Lognormal} (-\mu ,\ \sigma ^{2}).$
• Сила: Если $X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$ затем $X^{a}\sim \operatorname {Lognormal} (a\mu ,\ a^{2}\sigma ^{2})$ для $a\neq 0.$

Умножение и деление независимых логнормальных случайных величин.

Если две независимые логнормальные переменные $X_{1}$ и $X_{2}$ умножаются [делятся], произведение [отношение] снова логарифмически нормальное, с параметрами $\mu =\mu _{1}+\mu _{2}$ [ $\mu =\mu _{1}-\mu _{2}$] и $\sigma$, где $\sigma ^{2}=\sigma _{1}^{2}+\sigma _{2}^{2}$. Это легко обобщить на произведение $n$ такие переменные.

В более общем смысле, если $X_{j}\sim \operatorname {Lognormal} (\mu _{j},\sigma _{j}^{2})$ являются $n$ независимые, логарифмически нормально распределенные переменные, тогда $Y=\textstyle \prod _{j=1}^{n}X_{j}\sim \operatorname {Lognormal} {\Big (}\textstyle \sum _{j=1}^{n}\mu _{j},\ \sum _{j=1}^{n}\sigma _{j}^{2}{\Big )}.$

Мультипликативная центральная предельная теорема

Смотрите также: закон Гибрата

Среднее геометрическое или мультипликативное значение $n$ независимые, одинаково распределенные, положительные случайные величины $X_{i}$ шоу, для $n\to \infty$, приблизительно логарифмически нормальное распределение с параметрами $\mu =E[\ln(X_{i})]$ и $\sigma ^{2}={\mbox{var}}[\ln(X_{i})]/n$, предполагая $\sigma ^{2}$ конечно.

На самом деле случайные величины не обязательно должны быть одинаково распределены. Этого достаточно для распределения $\ln(X_{i})$ чтобы все они имели конечную дисперсию и удовлетворяли другим условиям любого из многих вариантов центральной предельной теоремы .

Это широко известно как закон Гибрата .

Другой

Набор данных, возникающий в результате логарифмически нормального распределения, имеет симметричную кривую Лоренца (см. также коэффициент асимметрии Лоренца ).

Гармонический $H$, геометрический $G$ и арифметика $A$ средства этого распределения родственны; такое отношение определяется выражением

$H={\frac {G^{2}}{A}}.$

Логнормальные распределения бесконечно делимы . но они не являются стабильными дистрибутивами , из которых можно легко извлечь.

Связанные дистрибутивы

• Если $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ является нормальным распределением , то $\exp(X)\sim \operatorname {Lognormal} (\mu ,\sigma ^{2}).$
• Если $X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$ распределяется логнормально, тогда $\ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ является нормальной случайной величиной.
• Позволять $X_{j}\sim \operatorname {Lognormal} (\mu _{j},\sigma _{j}^{2})$ быть независимыми логарифмически нормально распределенными переменными с возможным изменением $\sigma$ и $\mu$ параметры и ${\textstyle Y=\sum _{j=1}^{n}X_{j}}$. Распределение $Y$ не имеет выражения в замкнутой форме, но может быть разумно аппроксимировано другим логнормальным распределением. $Z$ у правого хвоста. Его функция плотности вероятности в окрестности 0 была охарактеризована и оно не похоже ни на какое логарифмически нормальное распределение. Часто используемое приближение, предложенное Л.Ф. Фентоном (но ранее сформулированное Р.И. Уилкинсоном и математически обоснованное Марлоу). ) получается путем сопоставления среднего значения и дисперсии другого логарифмически нормального распределения: $${\begin{aligned}\sigma _{Z}^{2}&=\ln \!\left[{\frac {\sum e^{2\mu _{j}+\sigma _{j}^{2}}(e^{\sigma _{j}^{2}}-1)}{(\sum e^{\mu _{j}+\sigma _{j}^{2}/2})^{2}}}+1\right],\\\mu _{Z}&=\ln \!\left[\sum e^{\mu _{j}+\sigma _{j}^{2}/2}\right]-{\frac {\sigma _{Z}^{2}}{2}}.\end{aligned}}$$ В случае, если все $X_{j}$ имеют одинаковый параметр дисперсии $\sigma _{j}=\sigma$, эти формулы упрощаются до $${\begin{aligned}\sigma _{Z}^{2}&=\ln \!\left[(e^{\sigma ^{2}}-1){\frac {\sum e^{2\mu _{j}}}{(\sum e^{\mu _{j}})^{2}}}+1\right],\\\mu _{Z}&=\ln \!\left[\sum e^{\mu _{j}}\right]+{\frac {\sigma ^{2}}{2}}-{\frac {\sigma _{Z}^{2}}{2}}.\end{aligned}}$$

Для более точного приближения можно использовать метод Монте-Карло для оценки кумулятивной функции распределения, PDF и правого хвоста.

Сумма коррелированных случайных величин с логнормальным распределением также может быть аппроксимирована логнормальным распределением. $${\begin{aligned}S_{+}&=\operatorname {E} \left[\sum _{i}X_{i}\right]=\sum _{i}\operatorname {E} [X_{i}]=\sum _{i}e^{\mu _{i}+\sigma _{i}^{2}/2}\\\sigma _{Z}^{2}&=1/S_{+}^{2}\,\sum _{i,j}\operatorname {cor} _{ij}\sigma _{i}\sigma _{j}\operatorname {E} [X_{i}]\operatorname {E} [X_{j}]=1/S_{+}^{2}\,\sum _{i,j}\operatorname {cor} _{ij}\sigma _{i}\sigma _{j}e^{\mu _{i}+\sigma _{i}^{2}/2}e^{\mu _{j}+\sigma _{j}^{2}/2}\\\mu _{Z}&=\ln \left(S_{+}\right)-\sigma _{Z}^{2}/2\end{aligned}}$$

• Если $X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$ затем $X+c$ Говорят, что оно имеет трехпараметрическое логарифмически нормальное распределение с поддержкой $x\in (c,+\infty )$. $\operatorname {E} [X+c]=\operatorname {E} [X]+c$, $\operatorname {Var} [X+c]=\operatorname {Var} [X]$.
• Логнормальное распределение является частным случаем полуограниченного SU-распределения Джонсона .
• Если $X\mid Y\sim \operatorname {Rayleigh} (Y)$ с $Y\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$, затем $X\sim \operatorname {Suzuki} (\mu ,\sigma )$ ( Распространение Сузуки ).
• Заменитель логнормального, интеграл которого можно выразить через более элементарные функции. можно получить на основе логистического распределения , чтобы получить аппроксимацию CDF $$F(x;\mu ,\sigma )=\left[\left({\frac {e^{\mu }}{x}}\right)^{\pi /(\sigma {\sqrt {3}})}+1\right]^{-1}.$$ Это лог-логистическое распределение .

Статистический вывод

Оценка параметров

Для определения оценок максимального правдоподобия параметров логнормального распределения µ и σ мы можем использовать ту же процедуру, что и для нормального распределения . Обратите внимание, что $$L(\mu ,\sigma )=\prod _{i=1}^{n}{\frac {1}{x_{i}}}\varphi _{\mu ,\sigma }(\ln x_{i}),$$где $\varphi$ - функция плотности нормального распределения ${\mathcal {N}}(\mu ,\sigma ^{2})$. Следовательно, функция логарифмического правдоподобия равна $$\ell (\mu ,\sigma \mid x_{1},x_{2},\ldots ,x_{n})=-\sum _{i}\ln x_{i}+\ell _{N}(\mu ,\sigma \mid \ln x_{1},\ln x_{2},\dots ,\ln x_{n}).$$

Поскольку первый член постоянен по отношению к µ и σ , обеим логарифмическим функциям правдоподобия, $\ell$ и $\ell _{N}$, достигают своего максимума с тем же $\mu$ и $\sigma$. Следовательно, оценки максимального правдоподобия идентичны оценкам для нормального распределения наблюдений. $\ln x_{1},\ln x_{2},\dots ,\ln x_{n})$, $${\widehat {\mu }}={\frac {\sum _{i}\ln x_{i}}{n}},\qquad {\widehat {\sigma }}^{2}={\frac {\sum _{i}\left(\ln x_{i}-{\widehat {\mu }}\right)^{2}}{n}}.$$

Для конечного n оценка для $\mu$ является беспристрастным, но тот, который для $\sigma$ является предвзятым. Что касается нормального распределения, то несмещенная оценка $\sigma$ можно получить, заменив знаменатель n на n −1 в уравнении для ${\widehat {\sigma }}^{2}$.

Когда индивидуальные ценности $x_{1},x_{2},\ldots ,x_{n}$ недоступны, но среднее значение выборки ${\bar {x}}$ и стандартное отклонение s равно, то метод моментов можно использовать . Соответствующие параметры определяются по следующим формулам, полученным в результате решения уравнений на математическое ожидание $\operatorname {E} [X]$ и дисперсия $\operatorname {Var} [X]$ для $\mu$ и $\sigma$: $$\mu =\ln \left({\frac {\bar {x}}{\sqrt {1+{\widehat {\sigma }}^{2}/{\bar {x}}^{2}}}}\right),\qquad \sigma ^{2}=\ln \left(1+{{\widehat {\sigma }}^{2}}/{\bar {x}}^{2}\right).$$

Интервальные оценки

Дополнительная информация: Контрольный диапазон § Логнормальное распределение.

Самый эффективный способ получить интервальные оценки при анализе логарифмически нормально распределенных данных состоит в применении хорошо известных методов, основанных на нормальном распределении, к логарифмически преобразованным данным, а затем при необходимости обратного преобразования результатов.

Интервалы прогнозирования

Базовый пример — интервалы прогнозирования : для нормального распределения интервал $[\mu -\sigma ,\mu +\sigma ]$ содержит примерно две трети (68%) вероятности (или большой выборки) и $[\mu -2\sigma ,\mu +2\sigma ]$ содержат 95%. Следовательно, для логнормального распределения $$[\mu ^{*}/\sigma ^{*},\mu ^{*}\cdot \sigma ^{*}]=[\mu ^{*}{}^{\times }\!\!/\sigma ^{*}]$$ содержит 2/3, и $$[\mu ^{*}/(\sigma ^{*})^{2},\mu ^{*}\cdot (\sigma ^{*})^{2}]=[\mu ^{*}{}^{\times }\!\!/(\sigma ^{*})^{2}]$$ содержит 95% вероятности. Если использовать оценочные параметры, то в этих интервалах должны содержаться примерно одинаковые проценты данных.

Доверительный интервал для μ ^*

Используя этот принцип, обратите внимание, что доверительный интервал для $\mu$ является $[{\widehat {\mu }}\pm q\cdot {\widehat {\mathop {se} }}]$, где $\mathop {se} ={\widehat {\sigma }}/{\sqrt {n}}$ — стандартная ошибка, а q — 97,5%-ный квантиль распределения t с n-1 степенями свободы. Обратное преобразование приводит к доверительному интервалу для $\mu ^{*}$ (медиана) составляет: $$[{\widehat {\mu }}^{*}{}^{\times }\!\!/(\operatorname {sem} ^{*})^{q}]$$ с $\operatorname {sem} ^{*}=({\widehat {\sigma }}^{*})^{1/{\sqrt {n}}}$

Доверительный интервал для μ

В литературе обсуждается несколько вариантов расчета доверительного интервала для $\mu$ (среднее логарифмически нормального распределения). К ним относятся загрузочная загрузка , а также различные другие методы.

Экстремальный принцип энтропии для фиксации свободного параметра σ

В приложениях, $\sigma$ является параметром, который необходимо определить. Для растущих процессов, уравновешенных производством и диссипацией, использование экстремального принципа энтропии Шеннона показывает, что $$\sigma ={\frac {1}{\sqrt {6}}}$$

Затем это значение можно использовать для определения некоторого масштабного соотношения между точкой перегиба и максимальной точкой логарифмически нормального распределения. Это соотношение определяется основанием натурального логарифма, $e=2.718\ldots$и демонстрирует некоторое геометрическое сходство с принципом минимальной поверхностной энергии.Эти масштабные соотношения полезны для прогнозирования ряда процессов роста (распространение эпидемии, разбрызгивание капель, рост населения, скорость закручивания вихря в ванне, распределение языковых символов, профиль скорости турбулентности и т. д.).Например, логнормальная функция с такой $\sigma$ хорошо соответствует размеру вторично образующихся капель во время удара капли и распространение эпидемического заболевания.

Значение ${\textstyle \sigma =1{\big /}{\sqrt {6}}}$ используется для обеспечения вероятностного решения уравнения Дрейка.

Возникновение и применение

Логнормальное распределение важно при описании природных явлений. Многие процессы естественного роста обусловлены накоплением множества небольших процентных изменений, которые становятся аддитивными в логарифмическом масштабе. При соответствующих условиях регулярности распределение результирующих накопленных изменений будет все лучше аппроксимироваться логнормальным, как отмечалось выше в разделе « Мультипликативная центральная предельная теорема ». Это также известно как закон Гибрата , в честь Роберта Гибрата (1904–1980), который сформулировал его для компаний. Если скорость накопления этих небольших изменений не меняется со временем, рост становится независимым от размера. Даже если это предположение неверно, распределение размеров в любом возрасте вещей, которые растут с течением времени, имеет тенденцию быть логарифмически нормальным. Следовательно, референтные диапазоны для измерений у здоровых людей более точно оцениваются, если предположить логарифмически нормальное распределение, чем предполагая симметричное распределение относительно среднего значения.

Второе обоснование основано на наблюдении, что фундаментальные законы природы предполагают умножение и деление положительных переменных. Примерами могут служить простой закон гравитации, связывающий массы и расстояния с результирующей силой, или формула равновесных концентраций химических веществ в растворе, связывающая концентрации продуктов и продуктов. Предположение о логнормальном распределении задействованных переменных приводит в этих случаях к непротиворечивым моделям.

Конкретные примеры приведены в следующих подразделах. содержит обзор и таблицу логнормальных распределений из геологии, биологии, медицины, продуктов питания, экологии и других областей. представляет собой обзорную статью о логнормальном распределении в нейробиологии с аннотированной библиографией.

Поведение человека

• Длина комментариев, публикуемых на дискуссионных форумах в Интернете, подчиняется логарифмически нормальному распределению.
• Время пребывания пользователей на онлайн-статьях (шутки, новости и т. д.) подчиняется логарифмически нормальному распределению.
• Продолжительность шахматных партий имеет тенденцию подчиняться логарифмически нормальному распределению.
• Продолжительность начала акустических стимулов сравнения, соответствующих стандартному стимулу, соответствует логарифмически нормальному распределению.

Биология и медицина

• Меры размера живой ткани (длина, площадь кожи, вес).
• Инкубационный период заболеваний.
• Диаметры пятен банановых листьев, мучнистой росы на ячмене.
• Показано, что для высокозаразных эпидемий, таких как атипичная пневмония в 2003 году, если применяется государственная политика контроля вмешательства, число госпитализированных случаев удовлетворяет логарифмически нормальному распределению без свободных параметров, если предполагается энтропия, а стандартное отклонение определяется принцип максимальной скорости производства энтропии .
• Длина инертных придатков (волос, когтей, ногтей, зубов) биологических особей в направлении роста.
• Нормализованный подсчет считываний РНК-Seq для любой области генома может быть хорошо аппроксимирован логарифмически нормальным распределением.
• Длина считывания секвенирования PacBio соответствует логарифмически нормальному распределению.
• Определенные физиологические измерения, такие как артериальное давление взрослых людей (после разделения на мужские и женские субпопуляции).
• Несколько фармакокинетических переменных, таких как Cmax _и , период полувыведения константа скорости выведения .
• В нейробиологии распределение частоты срабатывания по популяции нейронов часто примерно логарифмически нормальное. Впервые это наблюдалось в коре головного мозга и полосатом теле. а затем в гиппокампе и энторинальной коре, и в других частях мозга. Кроме того, распределение внутреннего усиления и распределение синаптического веса кажутся логарифмически нормальными. также.
• Плотность нейронов в коре головного мозга из-за шумного процесса деления клеток во время развития нервной системы.
• В ведении операционных залов распределение продолжительности операции .
• По размерам лавин изломов в цитоскелете живых клеток наблюдается логнормальное распределение, при этом размеры раковых клеток значительно превышают размеры здоровых.

Химия

• Распределение частиц по размерам и распределение молярной массы .
• Концентрация редких элементов в минералах.
• Диаметры кристаллов в мороженом, капель масла в майонезе, пор в жмыхе какао.

Подобрано кумулятивное логарифмически нормальное распределение для максимального годового количества осадков за 1 день, см. подбор распределения.

Гидрология

• В гидрологии логарифмически нормальное распределение используется для анализа экстремальных значений таких переменных, как месячные и годовые максимальные значения суточного количества осадков и объемов речного стока.

Изображение справа, созданное с помощью CumFreq , иллюстрирует пример аппроксимации логарифмически нормального распределения для ранжированных годовых максимальных однодневных осадков, демонстрируя также 90% доверительный интервал, основанный на биномиальном распределении .

Данные об осадках представлены в виде координат на графике в рамках кумулятивного частотного анализа .

Социальные науки и демография

• В экономике есть данные, что доходы 97–99% населения распределяются логарифмически нормально. (Распределение людей с более высокими доходами соответствует распределению Парето ).
• Если распределение доходов соответствует логарифмически нормальному распределению со стандартным отклонением $\sigma$, то коэффициент Джини , обычно используемый для оценки неравенства доходов, можно рассчитать как $G=\operatorname {erf} \left({\frac {\sigma }{2}}\right)$ где $\operatorname {erf}$ — функция ошибок , поскольку $G=2\Phi \left({\frac {\sigma }{\sqrt {2}}}\right)-1$, где $\Phi (x)$ — кумулятивная функция распределения стандартного нормального распределения.
• В финансах , в частности в модели Блэка-Шоулза , изменения логарифма обменных курсов, индексов цен и индексов фондового рынка считаются нормальными. (эти переменные ведут себя как сложные проценты, а не как простые проценты, и поэтому являются мультипликативными). Однако некоторые математики, такие как Бенуа Мандельброт, утверждали, что что лог-распределения Леви с тяжелыми хвостами были бы более подходящей моделью, в частности, для анализа обвалов фондового рынка . Действительно, распределение цен на акции обычно имеет « толстый хвост» . Распределение изменений во время крахов фондового рынка с толстым хвостом делает недействительными предположения центральной предельной теоремы .
• В наукометрии количество цитирований журнальных статей и патентов подчиняется дискретному логнормальному распределению.
• Размеры городов (население) удовлетворяют закону Жибрата. Процесс роста размеров городов пропорционален и инвариантен относительно размера. Таким образом, согласно центральной предельной теореме , логарифм размера города имеет нормальное распределение.
• Число сексуальных партнеров, по-видимому, лучше всего описывается логнормальным распределением.

Технология

• В анализе надежности логарифмически нормальное распределение часто используется для моделирования времени ремонта ремонтопригодной системы.
• В беспроводной связи «локальная средняя мощность, выраженная в логарифмических значениях, таких как дБ или непер, имеет нормальное (т. е. гауссово) распределение». Кроме того, случайное препятствие радиосигналам из-за больших зданий и холмов, называемое затенением , часто моделируется как логарифмически нормальное распределение.
• Распределение частиц по размерам, полученное в результате измельчения случайными ударами, например, при шаровой мельнице .
• Распределение размеров общедоступных файлов аудио- и видеоданных ( типы MIME ) следует логарифмически нормальному распределению на пять порядков величины .
• Размеры файлов 140 миллионов файлов на персональных компьютерах под управлением ОС Windows, собранные в 1999 году.
• Размеры текстовых электронных писем (1990-е годы) и мультимедийных писем (2000-е годы).
• В компьютерных сетях и анализе интернет-трафика логарифмически нормальный считается хорошей статистической моделью, представляющей объем трафика в единицу времени. Это было показано путем применения надежного статистического подхода к большим группам реальных интернет-трасс. В этом контексте логарифмически нормальное распределение показало хорошую производительность в двух основных случаях использования: (1) прогнозирование доли времени, когда трафик превысит заданный уровень (для соглашения об уровне обслуживания или оценки пропускной способности канала), т. е. определение размеров канала на основе пропускной способности. обеспечение и (2) прогнозирование цен 95-го процентиля.
• при физическом тестировании , когда тест определяет время до отказа элемента при заданных условиях, данные часто лучше всего анализировать с использованием логнормального распределения.

См. также

• Распределение с тяжелым хвостом
• Модель потерь на трассе логарифмического расстояния
• Модифицированное логнормальное степенное распределение
• Медленное затухание

Дальнейшее чтение

• Кроу, Эдвин Л.; Симидзу, Кунио, ред. (1988), Логнормальные распределения, теория и приложения , Статистика: Учебники и монографии, вып. 88, Нью-Йорк: Marcel Dekker, Inc., стр. xvi+387, ISBN.  978-0-8247-7803-3 , МР   0939191 , Збл   0644.62014
• Эйчисон Дж. и Браун Дж. А. К. (1957) Логнормальное распределение , издательство Кембриджского университета.
• Лимперт, Э; Стахель, В; Эббт, М. (2001). «Логнормальные распределения в науках: ключи и подсказки» . Бионаука . 51 (5): 341–352. doi : 10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2 .
• Холгейт, П. (1989). «Логнормальная характеристическая функция». Коммуникации в статистике - теория и методы . 18 (12): 4539–4548. дои : 10.1080/03610928908830173 .
• Брукс, Роберт; Корсон, Джон; Донал, Уэльс (1994). «Цена индексных опционов, когда все базовые активы следуют логнормальной диффузии». Достижения в области исследований фьючерсов и опционов . 7 . ССРН   5735 .

Внешние ссылки

• Нормальное распределение – это логарифмически нормальное распределение.