Округление

Чтобы узнать о других значениях, см. Округление (значения) .

Графики результата y округления x с использованием различных методов. Для наглядности графики показаны смещенными от целочисленных y значений . В файле SVG наведите указатель мыши на метод, чтобы выделить его, а в браузерах с поддержкой SMIL щелкните его, чтобы выбрать или отменить выбор.

Округление или закругление означает замену числа значением приблизительным , которое имеет более короткое, простое или более явное представление. Например, заменив $ 23,4476 на $ 23,45 , дробь 312/937 на 1/3 или выражение √2 на 1,414 .

Округление часто выполняется для получения значения, которое легче сообщить и сообщить, чем исходное. Округление также может быть важным, чтобы избежать вводящего в заблуждение точного сообщения о вычисленном числе, измерении или оценке; например, количество, которое было вычислено как 123456 , но известно, что его точность составляет лишь несколько сотен единиц, обычно лучше указывать как «около 123500 ».

С другой стороны, округление точных чисел внесет некоторую ошибку округления в сообщаемый результат. Округление практически неизбежно при сообщении о большом количестве вычислений, особенно при делении двух чисел в целочисленной арифметике или арифметике с фиксированной запятой ; при вычислении математических функций , таких как квадратные корни , логарифмы и синусы ; или при использовании представления с плавающей запятой с фиксированным количеством значащих цифр . В последовательности вычислений эти ошибки округления обычно накапливаются и в некоторых плохо обусловленных случаях могут сделать результат бессмысленным.

Точное округление трансцендентных математических функций затруднено, поскольку количество дополнительных цифр, которые необходимо вычислить, чтобы решить, следует ли округлять в большую или меньшую сторону, не может быть известно заранее. Эта проблема известна как « дилемма столовщика ».

Округление имеет много общего с квантованием , которое происходит, когда физические величины необходимо закодировать числами или цифровыми сигналами .

Волнистый знак равенства ( ≈ приблизительно равно ) иногда используется для обозначения округления точных чисел, например 9,98 ≈ 10. Этот знак был введен Альфредом Джорджем Гринхиллом в 1892 году.

Идеальные характеристики методов округления включают в себя:

1. Округление должно выполняться функцией . Таким образом, когда одни и те же входные данные округляются в разных случаях, выходные данные не изменяются.
2. Расчеты, выполненные с округлением, должны быть близки к расчетам, выполненным без округления.
   • В результате (1) и (2) результат округления должен быть близок к входу, часто как можно ближе по некоторому показателю .
3. Чтобы считаться округлением, будет подмножеством домена , диапазон как правило, дискретным . Классический диапазон — это целые числа Z .
4. Округление должно сохранять симметрию , которая уже существует между доменом и диапазоном. При конечной точности (или дискретной области) это означает устранение смещения .
5. Метод округления должен быть полезен в информатике или человеческой арифметике, где используется конечная точность и скорость имеет большое значение.

Поскольку метод обычно не может удовлетворить всем идеальным характеристикам, существует множество различных методов округления.

Как правило, округление идемпотентно ; т. е. после округления числа повторное округление его до той же точности не изменит его значения. Функции округления также монотонны ; т. е. округление двух чисел с одинаковой абсолютной точностью не изменит их порядок (но может дать одно и то же значение). В общем случае дискретного диапазона они являются кусочно-постоянными функциями .

Виды округления

Типичные проблемы округления включают в себя:

Проблема округления	Пример ввода	Результат	Критерий округления
Приближение иррационального числа дробью	п	22/7	1-значный знаменатель
Приближение рационального числа дробью с меньшим знаменателем	399 / 941	3 / 7	1-значный знаменатель
Приближение дроби дробным десятичным числом	5 / 3	1.6667	4 десятичных знака
Приближение дробного десятичного числа единицей с меньшим количеством цифр	2.1784	2.18	2 десятичных знака
Приближение десятичного целого числа целым числом с большим количеством конечных нулей	23217	23200	3 значимые цифры
Приближение большого десятичного целого числа с использованием научной записи	300999999	3.01 × 10 8	3 значимые цифры
Приближение значения кратным указанной сумме	48.2	45	кратно 15
Приближение каждого из конечного набора действительных чисел целым числом так, чтобы сумма округленных чисел равнялась округленной сумме чисел.	⁠ ${\bigl \{}{\tfrac {3}{12}},{\tfrac {4}{12}},{\tfrac {5}{12}}{\bigr \}}$⁠	{0, 0, 1}	Сумма округленных элементов равна округленной сумме элементов

Округление до целого числа

Самая простая форма округления — замена произвольного числа целым числом. Все следующие режимы округления являются конкретными реализациями абстрактной процедуры round() с одним аргументом. Это настоящие функции (за исключением тех, которые используют случайность).

Направленное округление до целого числа

Эти четыре метода называются направленным округлением до целого числа , поскольку все смещения от исходного числа x до округленного значения y или от него направлены к одному и тому же предельному значению (0, +∞ или −∞) . Направленное округление используется в интервальной арифметике и часто требуется в финансовых расчетах.

Если x положительное значение, округление вниз аналогично округлению к нулю, а округление вверх аналогично округлению от нуля. Если x отрицательное значение, округление вниз аналогично округлению от нуля, а округление вверх аналогично округлению к нулю. В любом случае, если x — целое число, y — это просто x .

Если множество вычислений выполняется последовательно, выбор метода округления может оказать очень существенное влияние на результат. Известный случай связан с новым индексом , установленным Ванкуверской фондовой биржей в 1982 году. Первоначально он был установлен на уровне 1 000 000 (точность до трех знаков после запятой), а через 22 месяца упал примерно до 520, хотя рынок, казалось, рос. Проблема была вызвана тем, что индекс пересчитывался тысячи раз в день и всегда усекался (округлялся вниз) до трех знаков после запятой, таким образом, что накапливались ошибки округления. Пересчет индекса за тот же период с использованием округления до ближайшей тысячной, а не усечения, скорректировал значение индекса с 524,811 до 1098,892.

В приведенных ниже примерах sng( x ) относится к функции знака , примененной к исходному числу x .

Округление вниз

Можно округлить в меньшую сторону (или взять пол , или округлить в сторону отрицательной бесконечности ): y — наибольшее целое число, не превосходящее x .

$y=\mathrm {floor} (x)=\left\lfloor x\right\rfloor =-\left\lceil -x\right\rceil$

Например, 23,7 округляется до 23, а -23,2 округляется до -24.

Округление вверх

Можно также округлить в большую сторону (или взять максимальную величину , или округлить в сторону положительной бесконечности ): y — наименьшее целое число, не меньшее x .

$y=\operatorname {ceil} (x)=\left\lceil x\right\rceil =-\left\lfloor -x\right\rfloor$

Например, 23,2 округляется до 24, а -23,7 округляется до -23.

Округление к нулю

Можно также округлить к нулю (или усечь , или округлить от бесконечности ): y — целое число, ближайшее к x, такое, что оно находится между 0 и x (включительно); т.е. y — целая часть x без цифр дробной части.

$y=\operatorname {truncate} (x)=\operatorname {sgn}(x)\left\lfloor \left|x\right|\right\rfloor =-\operatorname {sgn}(x)\left\lceil -\left|x\right|\right\rceil ={\begin{cases}\left\lfloor x\right\rfloor &x\geq 0\\[5mu]\left\lceil x\right\rceil &x<0\end{cases}}$

Например, 23,7 округляется до 23, а -23,7 округляется до -23.

Округление от нуля

Можно также округлить от нуля (или округлить до бесконечности ): y — целое число, ближайшее к 0 (или, что эквивалентно, к x ), такое, что x находится между 0 и y (включительно).

$y=\operatorname {sgn}(x)\left\lceil \left|x\right|\right\rceil =-\operatorname {sgn}(x)\left\lfloor -\left|x\right|\right\rfloor ={\begin{cases}\left\lceil x\right\rceil &x\geq 0\\[5mu]\left\lfloor x\right\rfloor &x<0\end{cases}}$

Например, 23,2 округляется до 24, а -23,2 округляется до -24.

Округление до ближайшего целого числа

Эти шесть методов называются округлением до ближайшего целого числа . Для округления числа x до ближайшего целого числа требуется некоторое правило разрешения конфликтов для тех случаев, когда x находится ровно посередине между двумя целыми числами, то есть когда дробная часть x равна точно 0,5.

Если бы не дробные части по 0,5, ошибки округления, вносимые методом округления до ближайшего, были бы симметричными: для каждой дроби, округляемой в меньшую сторону (например, 0,268), существует дополнительная дробь (а именно 0,732), которая округляется на такую ​​же сумму.

При округлении большого набора чисел с фиксированной точкой с равномерно распределенными дробными частями ошибки округления по всем значениям, за исключением тех, которые имеют 0,5 дробной части, статистически компенсируют друг друга. Это означает, что ожидаемое (среднее) значение округленных чисел равно ожидаемому значению исходных чисел при удалении из набора чисел с дробной частью 0,5.

На практике обычно используются числа с плавающей запятой , которые имеют еще больше вычислительных нюансов, поскольку расположены не на одинаковом расстоянии друг от друга.

Округление половины вверх

Можно округлить половину в большую сторону (или округлить половину в сторону положительной бесконечности ). Это правило разрешения споров широко используется во многих дисциплинах. То есть средние значения x всегда округляются в большую сторону. Если дробная часть x равна ровно 0,5, то y = x + 0,5.

$y=\left\lfloor x+{\tfrac {1}{2}}\right\rfloor =-\left\lceil -x-{\tfrac {1}{2}}\right\rceil =\left\lceil {\tfrac {1}{2}}\lfloor 2x\rfloor \right\rceil$

Например, 23,5 округляется до 24, а -23,5 округляется до -23.

Некоторые языки программирования (например, Java и Python) используют слово «половина вверх» для обозначения округления половины от нуля , а не округления половины в сторону положительной бесконечности .

Этот метод требует проверки только одной цифры, чтобы определить направление округления в представлениях с дополнением до двух и подобных представлениях.

Округление половины вниз

Можно также округлить половину вниз (или округлить половину в сторону отрицательной бесконечности ) в отличие от более распространенного округления половины вверх . Если дробная часть x равна ровно 0,5, то y = x - 0,5.

$y=\left\lceil x-{\tfrac {1}{2}}\right\rceil =-\left\lfloor -x+{\tfrac {1}{2}}\right\rfloor =\left\lfloor {\tfrac {1}{2}}\lceil 2x\rceil \right\rfloor$

Например, 23,5 округляется до 23, а -23,5 округляется до -24.

Некоторые языки программирования (например, Java и Python) используют слово «половина вниз» для обозначения округления половины до нуля , а не округления половины до отрицательной бесконечности .

Округление половины в сторону нуля

Можно также округлить половину к нулю (или округлить половину от бесконечности ) в отличие от обычного округления половины от нуля . Если дробная часть x равна ровно 0,5, то y = x - 0,5, если x положителен, и y = x + 0,5, если x отрицателен.

$y=\operatorname {sgn}(x)\left\lceil \left|x\right|-{\tfrac {1}{2}}\right\rceil =-\operatorname {sgn}(x)\left\lfloor -\left|x\right|+{\tfrac {1}{2}}\right\rfloor$

Например, 23,5 округляется до 23, а -23,5 округляется до -23.

Этот метод обрабатывает положительные и отрицательные значения симметрично и, следовательно, не имеет общего положительного/отрицательного смещения, если исходные числа являются положительными или отрицательными с равной вероятностью. Однако он все еще имеет смещение к нулю.

Округление половины от нуля

Можно также округлить половину от нуля (или округлить половину в сторону бесконечности ), это правило разрешения конфликтов, которое обычно преподается и используется, а именно: если дробная часть x равна точно 0,5, то y = x + 0,5, если x положителен. и y = x - 0,5, если x отрицательное значение.

$y=\operatorname {sgn}(x)\left\lfloor \left|x\right|+{\tfrac {1}{2}}\right\rfloor =-\operatorname {sgn}(x)\left\lceil -\left|x\right|-{\tfrac {1}{2}}\right\rceil$

Например, 23,5 округляется до 24, а -23,5 округляется до -24.

Это может быть более эффективно на компьютерах, которые используют представление знаковых величин для округляемых значений, поскольку необходимо учитывать только первую пропущенную цифру, чтобы определить, округляется ли она в большую или меньшую сторону. Это один из методов округления до значащих цифр из-за его простоты.

Этот метод, также известный как коммерческое округление , обрабатывает положительные и отрицательные значения симметрично и, следовательно, не имеет общего положительного/отрицательного смещения, если исходные числа являются положительными или отрицательными с равной вероятностью. Однако он все еще имеет отклонение от нуля.

Он часто используется для конвертации валют и округления цен (когда сумма сначала конвертируется в наименьшую значительную часть валюты, например, в центы евро), поскольку это легко объяснить, просто рассматривая первую дробную цифру, независимо от дополнительных цифр. точные цифры или знак суммы (для строгой эквивалентности плательщика и получателя суммы).

Округление половины до четного

Можно также округлить половину до четного , правило разрешения ничьей без положительного/отрицательного смещения и без смещения в сторону/от нуля. Согласно этому соглашению, если дробная часть x равна 0,5, то y — четное целое число, ближайшее к x . Так, например, 23,5 становится 24, как и 24,5; однако -23,5 становится -24, как и -24,5. Эта функция минимизирует ожидаемую ошибку при суммировании округленных чисел, даже если входные данные в основном положительные или в основном отрицательные, при условии, что они не являются ни преимущественно четными, ни преимущественно нечетными.

Этот вариант метода округления до ближайшего также называется сходящимся округлением , статистическим округлением , голландским округлением , гауссовским округлением , нечетно-четным округлением , или банковское округление .

Это режим округления по умолчанию, используемый в операциях IEEE 754 для результатов в двоичных форматах с плавающей запятой.

Устраняя предвзятость, повторное сложение или вычитание независимых чисел, как при одномерном случайном блуждании , даст округленный результат с ошибкой, которая имеет тенденцию расти пропорционально квадратному корню из числа операций, а не линейно.

Однако это правило искажает распределение, увеличивая вероятность четов по сравнению с шансами. Обычно это менее важно чем погрешности, которые устраняются этим методом.

Округление половины до нечетной

Можно также округлить половину до нечетного — аналогичное правило для округления половины до четного. В этом подходе, если дробная часть x равна 0,5, то y — нечетное целое число, ближайшее к x . Так, например, 23,5 становится 23, как и 22,5; в то время как -23,5 становится -23, как и -22,5.

Этот метод также свободен от положительного/отрицательного смещения и смещения в сторону/от нуля, при условии, что числа, подлежащие округлению, не являются ни преимущественно четными, ни преимущественно нечетными. Он также разделяет свойство округления от половины до чета, искажая исходное распределение, поскольку увеличивает вероятность шансов по сравнению с четами. Этот метод использовался для расчета банковских балансов в Соединенном Королевстве при десятичной дроби своей валюты. .

Этот вариант почти никогда не используется в вычислениях, за исключением ситуаций, когда хочется избежать увеличения масштаба чисел с плавающей запятой, которые имеют ограниченный диапазон показателей. При округлении от половины до четного небесконечное число округляется до бесконечности, а небольшое денормализованное значение округляется до нормального ненулевого значения. По сути, этот режим предпочитает сохранять существующую шкалу связующих чисел, избегая, когда это возможно, результатов, выходящих за пределы допустимого диапазона, для систем счисления с четным основанием (например, двоичной и десятичной). .

Округление для подготовки к меньшей точности

Этот режим округления используется, чтобы избежать получения потенциально неправильного результата после нескольких округлений . Этого можно добиться, если все округления, кроме финального, выполняются с использованием RPSP, и только финальное округление использует режим, запрошенный извне.

При десятичной арифметике избегаются последние цифры 0 и 5; если имеется выбор между числами, младшая цифра которых равна 0 или 1, 4 или 5, 5 или 6, 9 или 0, то выбирается цифра, отличная от 0 или 5; в противном случае выбор произволен. IBM определяет, что в последнем случае должна выбираться цифра с меньшим значением. RPSP может применяться с шагом между двумя последовательными округлениями, составляющим одну цифру (например, округление до 1/10 может применяться после округления до 1/100).Например, при округлении до целого числа:

• 20,0 округляется до 20;
• 20.01, 20.1, 20.9, 20.99, 21, 21.01, 21.9, 21.99 округляются до 21;
• 22,0, 22,1, 22,9, 22,99 округляются до 22;
• 24,0, 24,1, 24,9, 24,99 округляются до 24;
• 25,0 округляется до 25;
• 25.01, 25.1 округляются до 26.

В примере из раздела « Двойное округление » округление 9,46 до десятичной дроби дает 9,4, а округление до целого числа, в свою очередь, дает 9.

В двоичной арифметике это округление также называется «округлением до нечетного» (не путать с « округлением до половины до нечетного »). Например, при округлении до 1/4 (0,01 в двоичном формате)

• x = 2,0 ⇒ результат — 2 (10,00 в двоичном формате).
• 2,0 < x < 2,5 ⇒ результат 2,25 (10,01 в двоичном формате).
• x = 2,5 ⇒ результат 2,5 (10,10 в двоичном формате).
• 2,5 < x < 3,0 ⇒ результат 2,75 (10,11 в двоичном формате).
• x = 3,0 ⇒ результат — 3 (11,00 в двоичном формате).

Для получения правильных результатов на каждом этапе округления необходимо удалять не менее 2 двоичных цифр, в противном случае могут появиться неправильные результаты. Например,

• От 3,125 RPSP до 1/4 ⇒ результат 3,25.
• С 3,25 RPSP до 1/2 ⇒ результат 3,5.
• 3,5 раунда от половины до чета до 1 ⇒ результат 4 (неверно).

Если ошибочный средний шаг удален, последнее округление до целого числа округляет 3,25 до правильного значения 3.

RPSP реализован аппаратно в IBM zSeries и pSeries .

Рандомизированное округление до целого числа

Попеременный тай-брейк

Один из методов, более неясный, чем большинство других, заключается в изменении направления при округлении числа на 0,5 дробной части. Все остальные округляются до ближайшего целого числа. Если дробная часть равна 0,5, выполните поочередное округление в большую или меньшую сторону: для первого появления дробной части 0,5 округляйте в большую сторону, для второго — округляйте в меньшую сторону и так далее. Альтернативно, первое округление на 0,5 дробной части может быть определено случайным начальным числом . «Вверх» и «вниз» могут быть любые два метода округления, противоположные друг другу – в сторону положительной бесконечности и в сторону от нуля или в сторону и в сторону от нуля.

Если появления 0,5 дробных частей происходят значительно чаще, чем перезапуск «подсчета» вхождений, то система фактически свободна от смещения. При гарантированном нулевом смещении это полезно, если числа необходимо суммировать или усреднять.

Случайный тай-брейк

Если дробная часть x равна 0,5, выберите y случайным образом между x + 0,5 и x − 0,5 с равной вероятностью. Все остальные округляются до ближайшего целого числа.

Подобно округлению половины до четного и округления половины до нечетного, это правило, по сути, лишено общей предвзятости, но оно также справедливо для четных и нечетных y значений . Преимущество по сравнению с альтернативным решением тай-брейка состоит в том, что последнее направление округления дробной части 0,5 не нужно «запоминать».

Стохастическое округление

Округление следующим образом до одного из ближайшего целого числа в сторону отрицательной бесконечности и ближайшего целого числа в сторону положительной бесконечности с вероятностью, зависящей от близости, называется стохастическим округлением и в среднем дает несмещенный результат.

$\operatorname {Round} (x)={\begin{cases}\lfloor x\rfloor &{\text{ with probability }}1-(x-\lfloor x\rfloor )=\lfloor x\rfloor -x+1\\[5mu]\lfloor x\rfloor +1&{\text{ with probability }}{x-\lfloor x\rfloor }\end{cases}}$

Например, 1,6 будет округлено до 1 с вероятностью 0,4 и до 2 с вероятностью 0,6.

Стохастическое округление может быть таким точным, каким никогда не может быть функция округления . Например, предположим, что кто-то начал с 0 и добавил к этому значению 0,3 сто раз, округляя промежуточную сумму между каждым добавлением. Результатом будет 0 при обычном округлении, но при стохастическом округлении ожидаемый результат будет 30, что соответствует тому же значению, полученному без округления. Это может быть полезно в машинном обучении , где при обучении можно итеративно использовать арифметику низкой точности. Стохастическое округление также является способом достижения одномерного сглаживания .

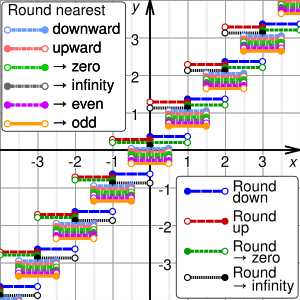
Сравнение подходов округления до целого числа

Ценить	Функциональные методы											Рандомизированные методы
	Направленное округление				Округлить до ближайшего						Закругление для подготовки к более короткой точности	Попеременный тай-брейк		Случайный тай-брейк		Стохастический
	Вниз (в сторону − ∞ )	Вверх (в сторону + ∞ )	К 0	Вдали от 0	Половина вниз (в сторону − ∞ )	Половина вверх (в сторону + ∞ )	Половина к 0	На полпути от 0	Половина к чету	Половина к нечетному		Средний	СД	Средний	СД	Средний	СД
+1.8	+1	+2	+1	+2	+2	+2	+2	+2	+2	+2	+1	+2	0	+2	0	+1.8	0.04
+1.5					+1		+1			+1		+1.505	0	+1.5	0.05	+1.5	0.05
+1.2						+1		+1	+1			+1	0	+1	0	+1.2	0.04
+0.8	0	+1	0	+1												+0.8	0.04
+0.5					0		0		0			+0.505	0	+0.5	0.05	+0.5	0.05
+0.2						0		0		0		0	0	0	0	+0.2	0.04
−0.2	−1	0		−1							−1					−0.2	0.04
−0.5					−1			−1		−1		−0.495	0	−0.5	0.05	−0.5	0.05
−0.8						−1	−1		−1			−1	0	−1	0	−0.8	0.04
−1.2	−2	−1	−1	−2												−1.2	0.04
−1.5					−2			−2	−2			−1.495	0	−1.5	0.05	−1.5	0.05
−1.8						−2	−2			−2		−2	0	−2	0	−1.8	0.04

Округление до других значений

Округление до заданного кратного

Самый распространенный тип округления — округление до целого числа; или, в более общем смысле, до целого числа, кратного некоторому приращению, например, округления до целых десятых долей секунды, сотых долей доллара, до целых кратных 1/2 или 1/8 дюйма, до целых десятков или тысяч и т. д.

В общем, округление числа x до кратного некоторому заданному положительному значению m влечет за собой следующие шаги:

$\mathrm {roundToMultiple} (x,m)=\mathrm {round} (x/m)\times m$

Например, округление x = 2,1784 доллара до целых центов (т. е. до кратного 0,01) влечет за собой вычисление 2,1784/0,01 = 217,84 , затем округление до 218 и, наконец, вычисление 218 × 0,01 = 2,18 .

При округлении до заранее определенного количества значащих цифр приращение m зависит от величины округляемого числа (или округленного результата).

Приращение m обычно представляет собой конечную дробь в любой системе счисления, используемой для представления чисел. Для отображения людям это обычно означает десятичную систему счисления (т. е. m — это целое число, умноженное на степень 10, например 1/1000 или 25/100). Для промежуточных значений, хранящихся в цифровых компьютерах, это часто означает двоичную систему счисления ( m — целое число, умноженное на степень 2).

Абстрактная функция round() с одним аргументом, которая возвращает целое число из произвольного действительного значения, имеет как минимум дюжину различных конкретных определений, представленных в разделе округления до целого числа . Здесь формально определена абстрактная функция roundToMultiple() с двумя аргументами, но во многих случаях она используется с неявным значением m = 1 для приращения, а затем сводится к эквивалентной абстрактной функции с одним аргументом, также с той же дюжиной. четкие конкретные определения.

Логарифмическое округление

Округление до указанной степени

Округление до указанной степени сильно отличается от округления до заданного кратного ; например, при вычислениях часто требуется округлить число до целой степени 2. В целом шаги по округлению положительного числа x до степени некоторого положительного числа b, отличного от 1, следующие:

$\mathrm {roundToPower} (x,b)=b^{\mathrm {round} (\log _{b}x)},x>0,b>0,b\neq 1$

Многие предостережения, применимые к округлению до кратного, применимы и к округлению в степень.

Масштабированное округление

Этот вид округления, который еще называют округлением в логарифмическом масштабе , представляет собой вариант округления в заданную степень . Округление по логарифмической шкале осуществляется путем взятия логарифма суммы и выполнения обычного округления до ближайшего значения логарифмической шкалы.

Например, резисторы поставляются с предпочтительными номерами в логарифмическом масштабе. В частности, для резисторов с точностью до 10% поставляют номиналы 100, 120, 150, 180, 220 и т.д., округленные до кратных 10 ( серия Е12 ). Если расчет показывает, что требуется резистор сопротивлением 165 Ом, тогда log(150) = 2,176 , log(165) = 2,217 и log(180) = 2,255 . Логарифм 165 ближе к логарифму 180, поэтому резистор сопротивлением 180 Ом будет первым выбором, если нет других соображений.

Округляется ли значение x ∈ ( a , b ) до a или b, зависит от того, является ли квадрат значения x ² больше или меньше произведения ab . В примере с резисторами значение 165 округляется до 180, поскольку 165 ² = 27225 больше, чем 150 × 180 = 27000 .

Округление с плавающей запятой

В арифметике с плавающей запятой цель округления — превратить заданное значение x в значение y с указанным количеством значащих цифр. Другими словами, y должно быть кратно числу m , которое зависит от величины x . Число m представляет собой степень по основанию (обычно 2 или 10) представления с плавающей запятой.

Помимо этой детали, все варианты округления, рассмотренные выше, применимы и к округлению чисел с плавающей запятой. Алгоритм такого округления представлен в разделе «Масштабированное округление» выше, но с постоянным коэффициентом масштабирования s = 1 и целочисленным основанием b > 1 .

Если округленный результат переполняет результат направленного округления, это либо соответствующая бесконечность со знаком при «округлении от нуля», либо наибольшее представимое положительное конечное число (или наименьшее представимое отрицательное конечное число, если x отрицательно), когда «округление» к нулю». Результатом переполнения для обычного случая округления до ближайшего всегда является соответствующая бесконечность.

Округление до простой дроби

В некоторых контекстах желательно округлить данное число x до «чистой» дроби, то есть до ближайшей дроби y = m / n, числитель m и знаменатель которой которой не превышают заданный максимум. Эта проблема существенно отличается от проблемы округления значения до фиксированного числа десятичных или двоичных цифр или до числа, кратного заданной единице m . Эта проблема связана с последовательностями Фарея , деревом Штерна–Броко и цепными дробями .

Округление до доступного значения

Готовые пиломатериалы , писчая бумага, конденсаторы и многие другие товары обычно продаются только в нескольких стандартных размерах.

Многие процедуры проектирования описывают, как вычислить приблизительное значение, а затем «округлить» до некоторого стандартного размера, используя такие фразы, как «округлить до ближайшего стандартного значения», «округлить до ближайшего стандартного значения» или «округлить до ближайшего стандартного значения». .

Когда набор предпочтительных значений равномерно распределен по логарифмической шкале, выбор наиболее близкого предпочтительного значения к любому заданному значению можно рассматривать как форму масштабированного округления . Такие округленные значения можно вычислить напрямую.

Произвольные контейнеры

Более общие правила округления могут разделять значения в произвольных точках останова, что используется, например, при объединении данных . Связанный математически формализованный инструмент — это последовательности указателей , которые используют понятия расстояния, отличные от простой разности — например, последовательность может округляться до целого числа с наименьшей относительной (процентной) ошибкой.

Округление в других контекстах

Дизеринг и диффузия ошибок

При оцифровке непрерывных сигналов , таких как звуковые волны, общий эффект ряда измерений более важен, чем точность каждого отдельного измерения. В таких случаях сглаживание и связанный с ним метод — диффузия ошибок обычно используются . Похожий метод, называемый широтно-импульсной модуляцией, используется для получения выходного сигнала аналогового типа от инерционного устройства путем быстрой подачи импульсов мощности с переменным рабочим циклом.

Распространение ошибок пытается обеспечить минимизацию ошибки в среднем. При плавном наклоне от единицы до нуля выходной сигнал будет нулевым для первых нескольких членов, пока сумма ошибки и текущее значение не станут больше 0,5, и в этом случае на выходе выводится 1, а разность вычитается из ошибки. до сих пор. Сглаживание Флойда – Стейнберга — популярная процедура диффузии ошибок при оцифровке изображений.

В качестве одномерного примера предположим, что числа 0,9677 , 0,9204 , 0,7451 и 0,3091 встречаются по порядку, и каждое из них необходимо округлить до кратного 0,01 . В этом случае совокупные суммы 0,9677 , 1,8881 = 0,9677 + 0,9204 , 2,6332 = 0,9677 + 0,9204 + 0,7451 и 2,9423 = 0,9677 + 0,9204 + 0,7451 + 0,3091 являются каждым раундом. кратно 0,01 : 0,97 , 1,89 , 2,63 и 2.94 . Первое из них и разность соседних значений дают желаемые округленные значения: 0,97 , 0,92 = 1,89 - 0,97 , 0,74 = 2,63 - 1,89 и 0,31 = 2,94 - 2,63 .

Арифметика Монте-Карло

Арифметика Монте-Карло — это метод метода Монте-Карло , при котором округление производится случайным образом в большую или меньшую сторону. Стохастическое округление можно использовать для арифметики Монте-Карло, но в целом чаще используется просто округление в большую или меньшую сторону с равной вероятностью. Повторные прогоны дадут случайное распределение результатов, что может указывать на стабильность вычислений.

Точные вычисления с округленной арифметикой

Можно использовать округленную арифметику для вычисления точного значения функции с целочисленным доменом и диапазоном. Например, если известно, что целое число n является точным квадратом, его квадратный корень можно вычислить путем преобразования n с плавающей запятой в значение z , вычисления приблизительного квадратного корня x из z с плавающей запятой, а затем округления x до ближайшее целое число y . Если n не слишком велико, ошибка округления с плавающей запятой в x будет меньше 0,5, поэтому округленное значение y будет точным квадратным корнем из n . По сути, именно поэтому логарифмические линейки можно использовать для точной арифметики.

Двойное округление

Двойное округление числа подряд до разных уровней точности, причем последняя точность является более грубой, не гарантирует того же результата, что и однократное округление до конечной точности, за исключением случая направленного округления. Например, округление 9,46 до одной десятичной дроби дает 9,5, а затем 10 при округлении до целого числа с использованием округления от половины до четного, но дает 9 при непосредственном округлении до целого числа. Борман и Чатфилд обсудить последствия двойного округления при сравнении данных, округленных до одного десятичного знака, с пределами спецификации, выраженными с использованием целых чисел.

В делах Мартинес против Олстейт и Сендехо против Фармерс , которые рассматривались в период с 1995 по 1997 год, страховые компании утверждали, что двойное округление страховых взносов допустимо и фактически необходимо. Суды США вынесли решение против страховых компаний и обязали их принять правила, обеспечивающие единое округление.

Некоторые компьютерные языки и стандарт IEEE 754-2008 требуют, чтобы при простых вычислениях результат не округлялся дважды. приходилось использовать специальные приемы программирования . x87 Это была особая проблема с Java, поскольку она спроектирована для одинакового запуска на разных машинах, и для достижения этого с плавающей запятой Язык Java был изменен, чтобы разрешить получение разных результатов там, где разница не имеет значения, и потребовать strictfp использования квалификатора , когда результаты должны точно соответствовать; строгая плавающая запятая была восстановлена ​​в Java 17.

В некоторых алгоритмах промежуточный результат вычисляется с большей точностью, а затем его необходимо округлить до конечной точности. Двойного округления можно избежать, выбрав подходящее округление для промежуточных вычислений. Это заключается в том, чтобы избежать округления до средних точек для окончательного округления (за исключением случаев, когда средняя точка является точной). В двоичной арифметике идея состоит в том, чтобы округлить результат в сторону нуля и установить младший бит равным 1, если округленный результат неточен; такое округление называется липким округлением . Эквивалентно, он состоит в возврате промежуточного результата, когда он точно представим, и ближайшего числа с плавающей запятой с нечетным мантиссом в противном случае; вот почему это также известно как округление до нечетного . Конкретная реализация этого подхода для двоичной и десятичной арифметики реализована как округление для подготовки к меньшей точности .

Дилемма столовщика

Уильям М. Кахан ввёл термин «Дилемма столовщика» для обозначения неизвестной стоимости округления трансцендентных функций :

Никто не знает, сколько будет стоить вычислить y. ^В правильно округляется для каждых двух аргументов с плавающей запятой, при которых не происходит переполнения/недополнения. Вместо этого авторитетные математические библиотеки вычисляют элементарные трансцендентные функции в основном в пределах чуть более половины ulp и почти всегда в пределах одного ulp. Почему ты не можешь ^В округляться с точностью до половины, как SQRT? Потому что никто не знает, сколько это будет стоить вычислений... Не существует общего способа предсказать, сколько дополнительных цифр придется перенести, чтобы вычислить трансцендентное выражение и правильно округлить его до некоторого заранее заданного количества цифр. Даже тот факт (если это правда), что конечного числа дополнительных цифр в конечном итоге будет достаточно, может оказаться глубокой теоремой.

Стандарт IEEE 754 для операций с плавающей запятой гарантирует, что сложение, вычитание, умножение, деление, объединенное умножение-сложение , квадратный корень и остаток с плавающей запятой дадут правильно округленный результат операции с бесконечной точностью. В стандарте 1985 года такой гарантии не было дано для более сложных функций, и они обычно имеют точность в лучшем случае только до последнего бита. Однако стандарт 2008 года гарантирует, что соответствующие реализации будут давать правильно округленные результаты, соответствующие активному режиму округления; однако реализация функций не является обязательной.

Используя теорему Гельфонда-Шнайдера и теорему Линдеманна-Вейерштрасса , можно доказать, что многие стандартные элементарные функции возвращают трансцендентные результаты, за исключением некоторых хорошо известных аргументов; поэтому с теоретической точки зрения всегда можно правильно округлить такие функции. Однако для реализации такой функции определение предела заданной точности того, насколько точные результаты должны быть вычислены, прежде чем можно будет гарантировать правильно округленный результат, может потребовать много времени вычислений или может быть недосягаемым. На практике, когда этот предел неизвестен (или известна только очень большая граница), при реализации необходимо принять какое-то решение (см. ниже); но согласно вероятностной модели правильное округление может быть обеспечено с очень высокой вероятностью при использовании промежуточной точности, до удвоенного количества цифр целевого формата плюс некоторая небольшая константа (после учета особых случаев).

Некоторые пакеты программирования предлагают правильное округление. Пакет GNU MPFR дает правильно округленные результаты произвольной точности. Некоторые другие библиотеки реализуют элементарные функции с правильным округлением в двойной точности IEEE 754 (binary64):

• IBM ml4j и Моше Ольшанским в , что означает Математическая библиотека для Java , написанная Авраамом Зивом 1999 году, правильно округляется только до ближайшего значения. Эта библиотека была заявлена ​​как портативная, но были предоставлены только двоичные файлы для PowerPC / AIX , SPARC / Solaris и x86 / Windows NT . Согласно документации, эта библиотека использует первый шаг с точностью немного большей двойной точности, второй шаг основан на арифметике double-double и третий шаг с точностью 768 бит основан на массивах двойной точности IEEE 754. числа с плавающей запятой.
• IBM Портативная математическая библиотека Accurate (сокращенно APMathLib или просто MathLib), также называемый либултимом, только с округлением до ближайшего. Эта библиотека использует до 768 бит рабочей точности. Он был включен в библиотеку GNU C в 2001 году. а вот «медленные пути» (при условии правильного округления) убрали с 2018 на 2021 год.
• CRlibm, написанная старой командой Arénaire (LIP, ENS Lyon ), впервые распространенная в 2003 году. Он поддерживает 4 режима округления и проверен с использованием знаний о самых сложных для округления случаях. Более эффективен, чем IBM MathLib. На смену ему пришла Metalibm (2014), которая автоматизирует формальные доказательства.
• libmcr от Sun Microsystems 2004 года, в 4 режимах округления. В сложных случаях эта библиотека также использует множественную точность, и количество слов увеличивается на 2 каждый раз, когда возникает дилемма Составителя таблиц (с неопределенным поведением в том очень маловероятном случае, когда достигается некоторый предел машины).
• Проект CORE-MATH (2022 г.) предоставляет некоторые правильно округленные функции в четырех режимах округления для процессоров x86-64 . Доказано с использованием знаний самых сложных для решения случаев.
• LLVM libc предоставляет некоторые правильно округленные функции в 4 режимах округления.

Существуют вычислимые числа , для которых невозможно определить округленное значение, сколько бы цифр ни вычислялось. Конкретные примеры привести невозможно, но это следует из неразрешимости проблемы остановки . Например, если гипотеза Гольдбаха верна, но , то результат округления следующего значения n недоказуема до следующего целого числа не может быть определен: либо n =1+10 ^{- к} где k — первое четное число, большее 4, которое не является суммой двух простых чисел, или n = 1, если такого числа нет. Округленный результат равен 2, если такое число k существует, и 1 в противном случае. Однако значение до округления может быть аппроксимировано с любой заданной точностью, даже если гипотеза недоказуема.

Взаимодействие со строковым поиском

Округление может отрицательно повлиять на строковый поиск числа. Например, π, округленное до четырех цифр, — это «3,1416», но простой поиск по этой строке не обнаружит «3,14159» или любое другое значение π, округленное до более чем четырех цифр. Напротив, усечение не страдает от этой проблемы; например, простой поиск строки по запросу «3,1415», представляющему собой число π, усеченное до четырех цифр, обнаружит значения π, усеченные до более чем четырех цифр.

История

Концепция округления очень старая, возможно, старше, чем сама концепция деления. Некоторые древние глиняные таблички, найденные в Месопотамии, содержат таблицы с округленными значениями обратных величин и квадратными корнями по основанию 60. Округленные приближения к π , длине года и длине месяца также являются древними — см. примеры по основанию 60 .

Метод округления от половины до чета используется в качестве американского стандарта Z25.1 и стандарта ASTM E-29 с 1940 года. Происхождение терминов « несмещенное округление» и «статистическое округление» достаточно понятно. В четвертом издании « Вероятности и теории ошибок» 1906 года Роберт Симпсон Вудворд назвал это «правилом компьютера». что указывает на то, что тогда он широко использовался людьми-компьютерами для расчета математических таблиц. Например, это было рекомендовано в книге Саймона Ньюкомба c. Книга 1882 года «Логарифмические и другие математические таблицы» . Люциуса Таттла 1916 года В «Теории измерений» это названо «универсально принятым правилом» записи физических измерений. Черчилль Эйзенхарт отметил, что эта практика уже «хорошо укоренилась» в анализе данных к 1940-м годам.

Происхождение термина «банковское округление» остается более неясным. Если этот метод округления когда-либо был стандартом в банковской сфере, найти доказательства оказалось чрезвычайно трудно. Напротив, раздел 2 доклада Европейской комиссии « Введение евро и округление денежных сумм» предполагает, что ранее в банковской сфере не существовало стандартного подхода к округлению; и в нем указано, что «половинные» суммы следует округлять в большую сторону.

До 1980-х годов метод округления, используемый в компьютерной арифметике с плавающей запятой, обычно фиксировался аппаратным обеспечением, был плохо документирован, непоследователен и различен для каждой марки и модели компьютера. Ситуация изменилась после того, как стандарт IEEE 754 с плавающей запятой был принят большинством производителей компьютеров. Стандарт позволяет пользователю выбирать один из нескольких режимов округления и в каждом случае точно определяет, как следует округлять результаты. Эти функции сделали численные вычисления более предсказуемыми и машинонезависимыми, а также сделали возможным эффективную и последовательную реализацию интервальной арифметики .

В настоящее время во многих исследованиях принято округлять числа, кратные 5 или 2. Например, Йорг Батен во многих исследованиях использовал возрастную кучу для оценки уровня умения считать у древних популяций. Он придумал индекс ABCC , который позволяет сравнивать навыки счета населения . грамотность между регионами без каких-либо исторических источников, в которых измерялась

Функции округления в языках программирования

Большинство языков программирования предоставляют функции или специальный синтаксис для округления дробных чисел различными способами. Самые ранние числовые языки, такие как FORTRAN и C , предоставляли только один метод, обычно усечение (в сторону нуля). Этот метод по умолчанию может подразумеваться в определенных контекстах, например, при присвоении дробного числа целочисленной переменной или использовании дробного числа в качестве индекса массива . Другие виды округления нужно было запрограммировать явно; например, округление положительного числа до ближайшего целого числа можно реализовать путем добавления 0,5 и усечения.

Однако в последние десятилетия синтаксис и стандартные библиотеки большинства языков обычно предоставляют как минимум четыре основные функции округления (вверх, вниз, до ближайшего и к нулю). Метод разрешения конфликтов может варьироваться в зависимости от языка и версии или может быть выбран программистом. Некоторые языки следуют примеру стандарта IEEE 754 с плавающей запятой и определяют эти функции как принимающие аргумент с плавающей запятой двойной точности и возвращающие результат того же типа, который затем при необходимости может быть преобразован в целое число. Этот подход позволяет избежать ложных переполнений , поскольку типы с плавающей запятой имеют больший диапазон, чем целочисленные типы. Некоторые языки, такие как PHP , предоставляют функции, которые округляют значение до указанного количества десятичных цифр (например, от 4321,5678 до 4321,57 или 4300). Кроме того, многие языки предоставляют функцию printf или аналогичную функцию форматирования строк, которая позволяет преобразовать дробное число в строку, округленную до заданного пользователем количества десятичных знаков ( точность ). С другой стороны, усечение (округление до нуля) по-прежнему является методом округления по умолчанию, используемым во многих языках, особенно для деления двух целочисленных значений.

Напротив, CSS и SVG не определяют какой-либо конкретной максимальной точности для чисел и измерений, которые они обрабатывают и отображают в своей DOM и в своем IDL- интерфейсе как строки, как если бы они имели бесконечную точность , и не делают различия между целыми числами и числами с плавающей запятой. ценности; однако реализации этих языков обычно преобразуют эти числа в значения с плавающей запятой двойной точности IEEE 754, прежде чем предоставлять вычисленные цифры с ограниченной точностью (особенно в стандартном JavaScript или ECMAScript). привязки интерфейса).

Другие стандарты округления

Некоторые дисциплины или учреждения издали стандарты или директивы по округлению.

наблюдения за погодой в США

В руководстве, выпущенном в середине 1966 г., Управление Федерального координатора по метеорологии США определило, что данные о погоде следует округлять до ближайшего круглого числа с использованием правила разделения «половина вверх». Например, 1,5, округленное до целого числа, должно стать 2, а -1,5 должно стать -1. До этой даты правило тай-брейка было «на половине раунда от нуля».

Отрицательный ноль в метеорологии

Основная статья: Знаковый ноль § В округленных значениях, таких как температура.

Некоторые метеорологи могут писать «-0», чтобы указать температуру от 0,0 до -0,5 градусов (исключительно), округленную до целого числа. Это обозначение используется, когда отрицательный знак считается важным, независимо от того, насколько мала его величина; например, при округлении температуры по шкале Цельсия , где ниже нуля указывает на замерзание.

См. также

• Округление денежных средств , связанное с отсутствием монет чрезвычайно низкой стоимости.
• Биннинг данных , аналогичная операция
• Точные таблицы Гала
• Защитная цифра
• Интервальная арифметика
• ИСО/МЭК 80000
• Алгоритм суммирования Кахана
• Пропорциональное представительство в партийных списках - тщательно исследованное применение округления целых чисел.
• Знаковое представление цифр
• Усечение

Внешние ссылки

• Вайсштейн, Эрик В. «Округление» . Математический мир .
• Введение в различные алгоритмы округления , доступное широкой аудитории, но особенно полезное для тех, кто изучает информатику и электронику.
• Как реализовать пользовательские процедуры округления от Microsoft (не работает)