Дигидрокатион

Дигидрокатион

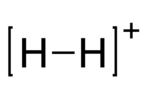Идентификаторы
Номер CAS	12184-90-6 DД2 + : 12184-84-8
3D model ( JSmol )	Интерактивное изображение 1 Ч 2 + : Интерактивное изображение DД2 + : Интерактивное изображение Т 2 + : Интерактивное изображение
ЧЭБИ	ЧЕБИ:29293 1 Ч 2 + : ЧЭБИ:29297 DД2 + : ЧЕБИ:29295 Т 2 + : ЧЭБИ:29296
Панель управления CompTox ( EPA )	DTXSID9029643
показывать ИнЧИ InChI=1S/H2/h1H/q+1 Key: ZZIJOQHRUPVPQC-UHFFFAOYSA-N 1H2+: InChI=1S/H2/h1H/q+1/i1+0H Key: ZZIJOQHRUPVPQC-HXFQMGJMSA-N D2+: InChI=1S/H2/h1H/q+1/i1+1D Key: ZZIJOQHRUPVPQC-VVKOMZTBSA-N T2+: InChI=1S/H2/h1H/q+1/i1+2T Key: ZZIJOQHRUPVPQC-JMRXTUGHSA-N
показывать УЛЫБКИ [HH+] 1H2+: [1H][1H+] D2+: [2H][2H+] T2+: [3H][3H+]
Характеристики
Химическая формула	Ч 2 +
Молярная масса	2.015  g·mol −1
Если не указано иное, данные приведены для материалов в стандартном состоянии (при 25 °C [77 °F], 100 кПа). Ссылки на инфобоксы

Катион диводорода или молекулярный ион водорода представляет собой катион (положительный ион ) с формулой H ⁺
₂ . Он состоит из двух водорода ядер ( протонов ), каждое из которых имеет один общий электрон . Это простейший молекулярный ион .

Ион может образоваться в результате ионизации нейтральной молекулы водорода ( H
₂ ) электронным ударом. Обычно он образуется в молекулярных облаках в космосе под действием космических лучей .

Дигидрокатион представляет большой исторический, теоретический и экспериментальный интерес.Исторически он представляет интерес тем, что, имея только один электрон, уравнения квантовой механики , описывающие его структуру, могут быть решены приближенно и относительно прямолинейно, если пренебречь движением ядер, релятивистскими и квантовыми электродинамическими эффектами. Первое такое решение было получено О. Буррау в 1927 году, всего через год после публикации волновой теории квантовой механики.

Теоретический интерес возникает потому, что возможно точное математическое описание, учитывающее квантовое движение всех составляющих, а также взаимодействие электрона с полем излучения. Точность описания неуклонно улучшалась на протяжении более полувека, что в конечном итоге привело к созданию теоретической основы, позволяющей со сверхвысокой точностью предсказать энергии вращательных и колебательных уровней в основном электронном состоянии, которые в основном метастабильны.

Параллельно экспериментальный подход к изучению катиона претерпел фундаментальную эволюцию по сравнению с более ранними экспериментальными методами, использовавшимися в 1960-х и 1980-х годах. Используя передовые методы, такие как захват ионов и лазерное охлаждение, вращательные и колебательные переходы можно исследовать в чрезвычайно мелких деталях. Соответствующие частоты переходов можно точно измерить, а результаты сравнить с точными теоретическими предсказаниями. Другой подход к прецизионной спектроскопии основан на охлаждении в криогенной магнитоэлектрической ловушке ( ловушка Пеннинга ); здесь движение катионов охлаждается резистивно, а внутренняя вибрация и вращение затухают за счет спонтанного излучения. Тогда можно будет точно изучить переходы электронного спинового резонанса.

Эти достижения превратили катионы диводорода в еще одно семейство связанных систем, важных для определения фундаментальных констант атомной и ядерной физики, после семейства атомов водорода (включая водородоподобные ионы ) и семейства атомов гелия .

Физические свойства

Склеивание в H ⁺
₂ можно описать как ковалентную одноэлектронную связь которой , формальный порядок связи равен половине.

Энергия основного состояния иона равна -0,597 Хартри .

Длина связи в основном состоянии равна 2,00 боровского радиуса .

изотопологи

Катион диводорода имеет шесть изотопологов . Каждое из двух ядер может быть одним из следующих: протон (p, наиболее распространенный), дейтрон (d) или тритон (t).

• Ч + 2 = ¹ H + 2 (катион диводорода, общий)
• [HD] ⁺ = [ ¹ ЧАС ² ЧАС] ⁺ (катион водорода-дейтерия)
• Д + 2 = ² H + 2 (катион дидейтерия)
• [ХТ] ⁺ = [ ¹ ЧАС ³ ЧАС] ⁺ (катион водорода трития)
• [ДТ] ⁺ = [ ² ЧАС ³ ЧАС] ⁺ (катион дейтерия-трития)
• Т + 2 = ³ H + 2 (катион дитрита)

Квантово-механический анализ

Приближение зажатых ядер

Приблизительное описание диводородного катиона начинается с пренебрежения движением ядер — так называемое приближение зажатых ядер. Это хорошее приближение, поскольку ядра (протон, дейтрон или тритон) более чем в 1000 раз тяжелее электрона. Поэтому сначала рассматривается движение электрона для заданного (произвольного) расстояния ядро-ядро R . Электронная энергия молекулы E и расчет повторяется для разных значений R. вычисляется , Энергия ядро-ядерного отталкивания e ² /(4 π ε ₀ R ) необходимо добавить к электронной энергии, в результате чего получится полная энергия молекулы E _tot ( R ).

Энергия E является собственным значением уравнения Шредингера для одиночного электрона. Уравнение можно решить относительно простым способом из-за отсутствия электрон-электронного отталкивания ( электронной корреляции ). Волновое уравнение ( уравнение в частных производных ) распадается на два связанных обыкновенных дифференциальных уравнения при использовании вытянутых сфероидальных координат вместо декартовых координат.Аналитическое решение уравнения, волновая функция , следовательно, пропорционально произведению двух бесконечных степенных рядов . Численную оценку ряда можно легко выполнить на компьютере.Аналитические решения для собственных значений электронной энергии также являются обобщением . W-функции Ламберта который можно получить с помощью системы компьютерной алгебры в рамках экспериментального математического подхода.

В учебниках по квантовой химии и физике связывание молекулы в основном электронном состоянии обычно рассматривается с помощью простейшего возможного анзаца для волновой функции: (нормированной) суммы двух волновых функций водорода 1s с центрами на каждом ядре. Этот анзац правильно воспроизводит переплет, но численно неудовлетворителен.

Исторические заметки

Ранние попытки лечения H ⁺
₂ с использованием старой квантовой теории были опубликованы в 1922 году Карелом Ниссеном. и Вольфганг Паули , и в 1925 году Гарольдом Юри .

Первое успешное квантовомеханическое лечение H ⁺
₂ был опубликован датским физиком Ойвиндом Буррау в 1927 году. всего через год после публикации Эрвина Шрёдингера «Волновая механика» .

В 1928 году Лайнус Полинг опубликовал обзор, объединивший работу Буррау с работами Уолтера Хайтлера и Фрица Лондона по молекуле водорода. Полное математическое решение проблемы электронной энергии для H ⁺
₂ в приближении зажатых ядер была предоставлена ​​Уилсоном (1928) и Яффе (1934). Джонсон (1940) дает краткое изложение своего решения.

Решения уравнения Шредингера с зажатыми ядрами

Молекулярный ион водорода H ⁺
₂ с зажатыми ядрами A и B , межъядерным расстоянием R плоскостью симметрии M. и

Электронное волновое уравнение Шрёдингера для молекулярного иона водорода H ⁺
₂ с двумя фиксированными ядерными центрами, обозначенными A и B , и одним электроном, можно записать как

$\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V\right)\psi =E\psi ~,$

где V – электронно-ядерная функция потенциальной энергии Кулона:

$V=-{\frac {e^{2}}{4\pi \varepsilon _{0}}}\left({\frac {1}{r_{a}}}+{\frac {1}{r_{b}}}\right)$

и E - (электронная) энергия данного квантовомеханического состояния (собственного состояния), с функцией электронного состояния ψ = ψ ( r ) в зависимости от пространственных координат электрона. Аддитивный термин ⁠ 1 / R ⁠ , которое является постоянным для фиксированного межъядерного расстояния R , было исключено из потенциала V , поскольку оно просто смещает собственное значение. Расстояния между электроном и ядрами обозначаются r _a и r _b . В атомных единицах ( ħ = m = e = 4 π ε ₀ = 1) волновое уравнение имеет вид

$\left(-{\tfrac {1}{2}}\nabla ^{2}+V\right)\psi =E\psi \qquad {\mbox{with}}\qquad V=-{\frac {1}{r_{a}}}-{\frac {1}{r_{b}}}\;.$

В качестве начала координат выберем середину между ядрами. Из общих принципов симметрии следует, что волновые функции можно охарактеризовать своим поведением симметрии относительно операции обращения точечной группы i ( r ↦ − r ). Существуют волновые функции ψ _g ( r ), симметричные относительно i , и есть волновые функции ψ _u ( r ), которые антисимметричны относительно этой операции симметрии:

$\psi _{g/u}(-{\mathbf {r} })={}\pm \psi _{g/u}({\mathbf {r} })\;.$

Суффиксы g и u от немецкого gerade и ungerade ), встречающиеся здесь, обозначают поведение симметрии при операции инверсии точечной группы i . Их использование является стандартной практикой для обозначения электронных состояний двухатомных молекул, тогда как для атомных состояний термины четное и нечетное используются . Основное состояние (самое низкое состояние) H ⁺
₂ обозначается X ² С ⁺
_г или 1sσ _g и это гераде. Существует также первое возбужденное состояние A ² С ⁺
_u (2pσ _u ), что является негерадным.

Полные энергии ( E _tot , в единицах Хартри, атомная единица энергии) низших состояний молекулярного иона водорода H ⁺
₂ как функция межъядерного расстояния ( R , в боровских радиусах, атомная единица длины). Подробности смотрите в тексте.

Асимптотически (суммарные) собственные энергии E _{g / u} для этих двух нижних состояний имеют одинаковое асимптотическое разложение по обратным степеням межъядерного расстояния R :

$E_{g/u}=-{\frac {1}{2}}-{\frac {9}{4R^{4}}}+O\left(R^{-6}\right)+\cdots$

Эта и энергетические кривые включают межъядерный член 1/R . Фактическая разница между этими двумя энергиями называется расщеплением обменной энергии и определяется выражением:

$\Delta E=E_{u}-E_{g}={\frac {4}{e}}\,R\,e^{-R}\left[\,1+{\frac {1}{2R}}+O\left(R^{-2}\right)\,\right]$

межъядерного расстояния R. которое экспоненциально исчезает с увеличением Ведущий термин ⁠ 4 / e ⁠ Re ^{− Р} впервые был получен методом Гольштейна–Херринга . Аналогично, асимптотические разложения по степеням ⁠ 1 / R ⁠ были получены в высоком порядке Cizek et al. для десяти нижних дискретных состояний молекулярного иона водорода (случай зажатых ядер). Таким образом, для обычных двухатомных и многоатомных молекулярных систем обменную энергию очень трудно рассчитать на больших межъядерных расстояниях, но, тем не менее, она необходима для дальнодействующих взаимодействий, включая исследования, связанные с магнетизмом и эффектами перезарядки. Они имеют особое значение в физике звезд и атмосферы.

Энергии самых низких дискретных состояний показаны на графике выше. Их можно получить с любой точностью, используя компьютерную алгебру из обобщенной функции Ламберта W (см. уравнение (3) на этом сайте и ссылку. ). Первоначально они были получены численным методом с точностью до двойной точности с помощью самой точной доступной программы, а именно ODKIL. Красные сплошные линии — это ² С ⁺
_г говорится. Зеленые пунктирные линии ² С ⁺
_ты утверждаешь. Синяя пунктирная линия – это ² Π _u состояние, а розовая пунктирная линия — это ² Π _г состояние. Обратите внимание, что хотя обобщенные решения для собственных значений функции Ламберта W заменяют эти асимптотические разложения, на практике они наиболее полезны вблизи длины связи .

Полный гамильтониан H ⁺
₂ (как и для всех центросимметричных молекул) не коммутирует с операцией обращения точечной группы i из-за влияния ядерного сверхтонкого гамильтониана. Ядерный сверхтонкий гамильтониан может смешивать вращательные уровни электронных состояний g и u (так называемое орто - пара -смешивание) и вызывать орто - пара -переходы.

Приближение Борна-Оппенгеймера

Как только энергетическая функция E _tot ( R ) получена, можно вычислить квантовые состояния вращательного и колебательного движения ядер и, следовательно, молекулы в целом. Соответствующее «ядерное» уравнение Шредингера представляет собой одномерное обыкновенное дифференциальное уравнение, в котором расстояние ядро-ядро R. независимой координатой является Уравнение описывает движение фиктивной частицы с массой, равной приведенной массе двух ядер, в потенциале E _tot ( R )+ V _L ( R ), где второй член — центробежный потенциал, обусловленный вращением с угловым моментом описывается квантовым L. числом Собственные энергии этого уравнения Шредингера представляют собой полные энергии всей молекулы, электронной плюс ядерной.

Теория ab initio высокой точности

Приближение Борна-Оппенгеймера непригодно для описания дигидрокатиона достаточно точно, чтобы объяснить результаты прецизионной спектроскопии.

Полное уравнение Шредингера для этого катиона без приближения зажатых ядер гораздо более сложное, но тем не менее может быть решено численно практически точно с использованием вариационного подхода. Тем самым точно рассматривается одновременное движение электрона и ядер. Когда решения ограничиваются орбиталью с самой низкой энергией, можно получить энергии и волновые функции вращательных и колебательных состояний. Численная неопределенность энергий и волновых функций, найденных таким способом, незначительна по сравнению с систематической ошибкой, возникающей при использовании уравнения Шредингера, а не принципиально более точных уравнений. Действительно, уравнение Шрёдингера не включает в себя всю значимую физику, как это известно из проблемы атома водорода. Более точные методы лечения должны учитывать физику, описываемую уравнением Дирака или, что еще точнее, квантовой электродинамикой. Наиболее точные решения вращательно-колебательных состояний находятся с помощью нерелятивистской квантовой электродинамики ( NRQED ).

Для сравнения с экспериментом необходимы различия энергий состояний, т.е. частот переходов. Для переходов между вращательно-колебательными уровнями, имеющими малые вращательные и умеренные колебательные квантовые числа, частоты были рассчитаны с теоретической дробной неопределенностью примерно 8 × 10. ⁻¹² . Дополнительный вклад в неопределенность предсказанных частот возникает из-за неопределенностей фундаментальных констант , которые учитываются в теоретических расчетах, особенно из-за соотношения массы протона и массы электрона.

Используя сложный формализм ab initio, можно также точно рассчитать сверхтонкие энергии, см. Ниже.

Экспериментальные исследования

Прецизионная спектроскопия

Из-за своей относительной простоты катион диводорода является наиболее точно изученной молекулой в том смысле, что теоретические расчеты его энергетических уровней соответствуют экспериментальным результатам с наивысшим уровнем согласия.

В частности, спектроскопически определенные частоты чистых вращательных и колебательных переходов конкретного изотополога HD. ⁺ согласуются с теоретически рассчитанными частотами перехода. Четыре высокоточных эксперимента дали сравнения с общей погрешностью между 2 × 10 ⁻¹¹ и 5 × 10 ⁻¹¹ , дробно. Уровень согласия фактически ограничен ни теорией, ни экспериментом, а, скорее, неопределенностью текущих значений масс частиц, которые используются в качестве входных параметров расчета.

Чтобы измерить частоты переходов с высокой точностью, спектроскопию диводородного катиона пришлось проводить в особых условиях. Следовательно, ансамбли HD ⁺ Ионы были пойманы в квадрупольную ионную ловушку в сверхвысоком вакууме, сочувственно охлаждены ионами бериллия, охлажденными лазером , и исследованы с использованием определенных спектроскопических методов.

Сверхтонкая структура гомоядерного изотополога H ₂ ⁺ была тщательно и точно измерена Джеффертсом в 1969 году. Наконец, в 2021 году расчеты теории ab initio смогли предоставить количественные детали структуры с неопределенностью меньшей, чем неопределенность экспериментальных данных, 1 кГц . Теоретически подтверждены некоторые вклады в измеренную сверхтонкую структуру на уровне примерно 50 Гц .

m d _, Следствием этих соглашений является то, что можно вывести спектроскопическое значение отношения массы электрона к приведенной массе протона и дейтрона, me / что _{является} входными данными _для m p + me / теории _ab initio. Соотношение подбирается таким образом, чтобы теоретические предсказания и экспериментальные результаты согласовывались. Неопределенность полученного отношения сравнима с неопределенностью, полученной из прямых измерений масс протона, дейтрона, электрона и HD. ⁺ посредством циклотронного резонанса в ловушках Пеннинга .

Появление в космосе

Формирование

Ион диводорода образуется в природе при взаимодействии космических лучей и молекулы водорода. Электрон выбивается, оставляя катион.

H ₂ + космические лучи → H ⁺
₂₊ и ⁻ + космический луч.

Частицы космических лучей обладают достаточной энергией, чтобы ионизировать многие молекулы, прежде чем они остановятся.

Энергия ионизации молекулы водорода равна 15,603 эВ. Высокоскоростные электроны также вызывают ионизацию молекул водорода с пиковым сечением около 50 эВ. Пиковое сечение ионизации высокоскоростных протонов составляет 70 000 эВ при сечении 2,5 × 10 ⁻¹⁶ см ² . Протон космических лучей с более низкой энергией также может оторвать электрон от нейтральной молекулы водорода с образованием нейтрального атома водорода и катиона диводорода ( p ⁺ + Ч2 _→ Ч + Ч ⁺
₂ ) с пиковым сечением около эВ 8 × 8000 10 ⁻¹⁶ см ² .

Разрушение

В природе ион разрушается в результате реакции с другими молекулами водорода:

ЧАС ⁺
₂ + Ч ₂ → Ч ⁺
₃ + Х.

Производство в лаборатории

В лаборатории ион легко получить путем бомбардировки электронами из электронной пушки.

Искусственная плазменная разрядная ячейка также может производить ион.

См. также

• Симметрия двухатомных молекул
• Модель функции Дельта Дирака (одномерная версия H ⁺
  ₂ )
• Ди-позитроний
• Задача трех тел Эйлера (классический аналог)
• Малочастичные системы
• Атом гелия
• Ион гидрида гелия
• Триводородный катион
• Трехатомный водород
• Функция Ламберта W
• Молекулярная астрофизика
• Метод Гольштейна – Херринга
• Задача трех тел
• Список квантовомеханических систем с аналитическими решениями