Принцип Харди -Вайнберг

Пропорции Харди -Вейнберга для двух аллелей : горизонтальная ось показывает две частоты аллеля P и Q , а вертикальная ось показывают ожидаемые частоты генотипа . Каждая строка показывает один из трех возможных генотипов.

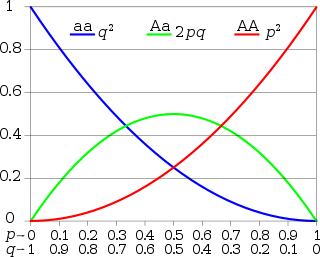
В генетике популяции принцип Харди -Вейнберга , также известный как равновесие Харди -Вайнберг , модель , теорема или закон , утверждает, что частоты аллеля и генотипа в популяции останутся постоянными от генерации до поколения в отсутствие других эволюционных влияний. Эти влияния включают генетический дрейф , выбор товарища , ассортативное спаривание , естественный отбор , половой отбор , мутацию , поток генов , мейотическое привод , генетическое автостопное управление , узкое место населения , эффект основателя , инбридинги и превзойдя депрессию .

В простейшем случае одного локуса с двумя аллелями , обозначенными A и A с частотами f (a) = p и f (a) = q , соответственно ожидаемые частоты генотипа при случайном спаривании являются f (aa) = p ² для AA -гомозигот , f (aa) = q ² Для гомозигот АА и F (AA) = 2 pq для гетерозигот . В отсутствие отбора, мутации, генетического дрейфа или других сил частоты аллелей P и Q постоянны между поколениями, поэтому достигается равновесие.

Принцип назван в честь Г.Х. Харди и Вильгельма Вайнберга , которые впервые продемонстрировали его математически. Документ Харди была сосредоточена на том, чтобы разоблачить мнение о том, что доминирующий аллель будет автоматически увеличиваться в частоте (точка зрения, возможно, на основе неверно истолкованного вопроса на лекции ) Сегодня тесты на частоты генотипа Харди-Вайнберга используются главным образом для проверки на стратификацию популяции и другие формы спаривания, не связанных с ними.

Вывод

Рассмотрим популяцию монодомных диплоидов , где каждый организм производит мужские и женские гаметы с одинаковой частотой и имеют два аллеля в каждом локусе гена. Мы предполагаем, что население настолько велика, что его можно рассматривать как бесконечное. Организмам размножается случайным союзом гамет (популяционная модель «генов»). Локус в этой популяции имеет два аллеля, a и a, которые встречаются с начальными частотами f ₀ (a) = p и f ₀ (a) = q соответственно. Частоты аллелей в каждом поколении получают путем объединения аллелей из каждого генотипа одного и того же поколения в соответствии с ожидаемым вкладом гомозиготы и гетерозиготных генотипов, которые составляют 1 и 1/2 соответственно:

$f_{t}({\text{A}})=f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})$ ( 1 )

$f_{t}({\text{a}})=f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})$ ( 2 )

Длина P , Q соответствует частотам аллеля (здесь p = 0,6, Q = 0,4 ). Затем область прямоугольника представляет частоты генотипа (таким образом, AA: AA: AA = 0,36: 0,48: 0,16 ).

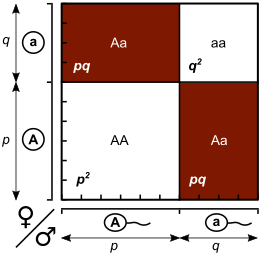
Различные способы формирования генотипов для следующего поколения могут быть показаны на квадрате Паннетта , где доля каждого генотипа равна продукту частот аллелей строк и столбцов из текущего поколения.

Таблица 1: Пуннетт -сквер для Харди -Вейнберга

		Женщины
		A ( P )	A ( Q )
Мужчины	A ( P )	Аа ( с 2 )	AA ( PQ )
	A ( Q )	AA ( QP )	АА ( кв 2 )

Сумма записей ² + 2 pq + q ² = 1 , так как частота генотипа должна суммироваться до одного.

Обратите внимание, что как p + q = 1 , биномиальное расширение ( P + Q ) ² = р ² + 2 pq + q ² = 1 дает те же отношения.

Суммируя элементы площади Паннетта или биномиальной экспансии, мы получаем ожидаемые пропорции генотипа среди потомства после одного поколения:

$f_{1}({\text{AA}})=p^{2}=f_{0}({\text{A}})^{2}$ ( 3 )

$f_{1}({\text{Aa}})=pq+qp=2pq=2f_{0}({\text{A}})f_{0}({\text{a}})$ ( 4 )

$f_{1}({\text{aa}})=q^{2}=f_{0}({\text{a}})^{2}$ ( 5 )

Эти частоты определяют равновесие Харди -Вайнберга. Следует упомянуть, что частоты генотипа после первого поколения не должны равняться частотам генотипа из начального поколения, например, F ₁ (AA) ≠ F ₀ (AA) . Тем не менее, частоты генотипа для всех будущих времен будут равны частотам выносливо -Вейнберга, например, f _t (aa) = f ₁ (aa) для t > 1 . Это следует, поскольку частоты генотипа следующего поколения зависят только от частот аллелей текущего поколения, которые, как рассчитываются уравнениями ( 1 ) и ( 2 ), сохраняются из начальной генерации:

${\begin{aligned}f_{1}({\text{A}})&=f_{1}({\text{AA}})+{\tfrac {1}{2}}f_{1}({\text{Aa}})=p^{2}+pq=p(p+q)=p=f_{0}({\text{A}})\\f_{1}({\text{a}})&=f_{1}({\text{aa}})+{\tfrac {1}{2}}f_{1}({\text{Aa}})=q^{2}+pq=q(p+q)=q=f_{0}({\text{a}})\end{aligned}}$

общего случая диологических диплоидов , которые размножаются путем случайного спаривания индивиду мужчинами, либо женщинами ] Для более организмов являются либо [ Любой пол, взвешенный в результате ожидаемого вклада генотипа каждого такого спаривания. Эквивалентно, кто учитывает шесть уникальных диплоид-диплоидных комбинаций:

$\left[({\text{AA}},{\text{AA}}),({\text{AA}},{\text{Aa}}),({\text{AA}},{\text{aa}}),({\text{Aa}},{\text{Aa}}),({\text{Aa}},{\text{aa}}),({\text{aa}},{\text{aa}})\right]$

и строит квадрат Паннетта для каждого, чтобы рассчитать его вклад в генотипы следующего поколения. Эти вклады взвешены в соответствии с вероятностью каждой диплоид-диплоидной комбинации, которая следует за многономиальным распределением с k = 3 . Например, вероятность комбинации спаривания (AA, AA) составляет 2 F _T (AA) F _T (AA) , и она может привести только к генотипу AA : [0,1,0] . В целом, полученные частоты генотипа рассчитываются как:

${\begin{aligned}&\left[f_{t+1}({\text{AA}}),f_{t+1}({\text{Aa}}),f_{t+1}({\text{aa}})\right]=\\&\qquad =f_{t}({\text{AA}})f_{t}({\text{AA}})\left[1,0,0\right]+2f_{t}({\text{AA}})f_{t}({\text{Aa}})\left[{\tfrac {1}{2}},{\tfrac {1}{2}},0\right]+2f_{t}({\text{AA}})f_{t}({\text{aa}})\left[0,1,0\right]\\&\qquad \qquad +f_{t}({\text{Aa}})f_{t}({\text{Aa}})\left[{\tfrac {1}{4}},{\tfrac {1}{2}},{\tfrac {1}{4}}\right]+2f_{t}({\text{Aa}})f_{t}({\text{aa}})\left[0,{\tfrac {1}{2}},{\tfrac {1}{2}}\right]+f_{t}({\text{aa}})f_{t}({\text{aa}})\left[0,0,1\right]\\&\qquad =\left[\left(f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)^{2},2\left(f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)\left(f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right),\left(f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)^{2}\right]\\&\qquad =\left[f_{t}({\text{A}})^{2},2f_{t}({\text{A}})f_{t}({\text{a}}),f_{t}({\text{a}})^{2}\right]\end{aligned}}$

Как и прежде, можно показать, что частоты аллелей в момент времени t + 1 равны тем, что в момент времени t , и поэтому они постоянны во времени. Точно так же частоты генотипа зависят только от частот аллелей, и поэтому после времени t = 1 также постоянны во времени.

Если в монодомных или диологических организмах, пропорции аллеля или генотипа изначально неравны в любом поне, можно показать, что постоянные пропорции получают после одного поколения случайного спаривания. Если диологические организмы являются гетерогаметическими , а локус генов расположен на Х -хромосоме , можно показать, что если частоты аллелей изначально неравны у двух полов [ , XX самки и самцы XY, как у людей], F например а) В гетерогаметическом положении «Чозбы» f (а) в гомогаметическом полу предыдущего поколения, пока равновесие не будет достигнуто при средневзвешенном уровне двух начальных частот.

Отклонения от равновесия Харди -Вайнберга

Семь допущений, лежащих в основе равновесия Харди -Вайнберга, следующие:

• Организмы диплоидны
• происходит только сексуальное воспроизведение
• Поколения не перекрываются
• Спаривание случайно
• Размер популяции бесконечно большой
• Частоты аллелей равны по полу
• нет миграции, потока генов, примесь, мутации или отбора

Нарушения допущений Харди -Вейнберга могут вызвать отклонения от ожидания. То, как это влияет на население, зависит от предположений, которые нарушаются.

• Случайное спаривание . HWP утверждает, что популяция будет иметь данные генотипические частоты (называемые пропорциями Харди -Вайнберга) после одного поколения случайного спаривания в популяции. Когда предположение о случайном спаривании нарушено, население не будет иметь пропорции Харди -Вайнберга. Распространенной причиной неспособности спаривания является инбридинга , что вызывает увеличение гомозиготности для всех генов.

Если население нарушает одно из следующих четырех допущений, население может продолжать иметь пропорции Харди -Вейнберга каждого поколения, но частоты аллелей будут меняться со временем.

• отбор В целом приводит к изменению частот аллелей, часто довольно быстро. В то время как направленный отбор в конечном итоге приводит к потере всех аллелей, за исключением предпочтительного (если только один аллель не является доминирующим, и в этом случае рецессивные аллели могут выжить на низких частотах), некоторые формы отбора, такие как баланс отбора , приводят к равновесию без потери аллели.
• Мутация будет оказывать очень тонкое влияние на частоты аллелей посредством введения нового аллеля в популяцию. Скорость мутаций порядок 10 ⁻⁴ до 10 ⁻⁸ и изменение частоты аллелей будет, в большинстве случаев, одинаковым порядком. Рецидивирующая мутация будет поддерживать аллели в популяции, даже если есть сильный выбор против них.
• Миграция генетически связывает две или более популяций вместе. В целом, частоты аллелей станут более однородными среди населения. Некоторые модели для миграции по своей природе включают нерушительное спаривание ( эффект Wahlund например, ). Для этих моделей пропорции Харди -Вайнберга обычно не будут действительны.
• Небольшой размер популяции может вызвать случайное изменение частот аллелей. Это связано с эффектом отбора проб и называется генетическим дрейфом . Эффекты отбора проб наиболее важны, когда аллель присутствует в небольшом количестве копий.

В данных генотипа в реальном мире отклонения от равновесия Харди -Вайнберга могут быть признаком ошибки генотипирования.

Половая связь

В тех случаях, когда ген A связан с сексом , гетерогаметический пол ( например , самцы млекопитающих; птицы) имеют только одну копию гена (и называются гемизиготными), в то время как гомогаметический пол ( например , у людей ) есть две копии. Частоты генотипа в равновесии являются P и Q для гетерогаметического пола, но P ² , 2 pq и q ² Для гомогаметического секса.

Например, у людей красный-зеленый цветовой пузырь -это рецессивная черта X. У мужчин в Западной Европе этот признак поражает около 1 на 12 ( Q = 0,083), тогда как она поражает около 1 из 200 женщин (0,005 по сравнению с Q ² = 0,007), очень близко к пропорциям Харди -Вейнберга.

Если популяция объединяется с мужчинами и женщинами с частотой аллелей в каждой субпопуляции (мужчин или женщин), частота аллеля среди мужского населения в следующем поколении будет следовать за частотой женской популяции, потому что каждый сын получает свою Х -хромосому от его мать. Население очень быстро сходится на равновесие.

Обобщения

Простой вывод выше может быть обобщен для более чем двух аллелей и полиплоидии .

Обобщение для более чем двух аллелей

Паннетт Площадь для дела с тремя аллелью (слева) и четырехлель (справа). Белые районы - гомозиготы. Цветные участки - гетерозиготы.

Рассмотрим дополнительную частоту аллелей, р . Случай с двумя аллелями- биномиальное расширение ( P + Q ) ² и, таким образом, случай с тремя аллелью является триномиальным расширением ( P + Q + R ) ² .

$(p+q+r)^{2}=p^{2}+q^{2}+r^{2}+2pq+2pr+2qr\,$

В более общем плане, рассмотрим аллели A ₁ , ..., _n, данный частотами аллелей P ₁ до P _n ;

$(p_{1}+\cdots +p_{n})^{2}\,$

дает всем гомозиготы :

$f(A_{i}A_{i})=p_{i}^{2}\,$

и для всех гетерозигот :

$f(A_{i}A_{j})=2p_{i}p_{j}\,$

Обобщение для полиплоидии

Принцип Харди -Вайнберга также может быть обобщен в полиплоидных системах, то есть для организмов, которые имеют более двух копий каждой хромосомы. Рассмотрим еще раз только два аллеля. Диплоидный случай является биномиальным расширением :

$(p+q)^{2}\,$

и, следовательно, полиплоидный случай является биномиальным расширением:

$(p+q)^{c}\,$

где C - плоидия , например, с тетраплоидом ( C = 4):

Таблица 2: Ожидаемые частоты генотипа для тетраплоидии

Генотип	Частота
Аааа	$p^{4}$
Аааа	$4p^{3}q$
Аааа	$6p^{2}q^{2}$
Аааа	$4pq^{3}$
аааа	$q^{4}$

Является ли организм «истинным» тетраплоидом или амфидиплоидом, будет определять, сколько времени потребуется, чтобы популяция достигнет равновесия Харди - Вайнберга.

Полное обобщение

Для $n$ Отдельные аллели в $c$-ploids, частоты генотипа в равновесии Харди -Вейнберга приводятся отдельными терминами в многономиальном расширении . $(p_{1}+\cdots +p_{n})^{c}$:

$(p_{1}+\cdots +p_{n})^{c}=\sum _{k_{1},\ldots ,k_{n}\ \in \mathbb {N} :k_{1}+\cdots +k_{n}=c}{c \choose k_{1},\ldots ,k_{n}}p_{1}^{k_{1}}\cdots p_{n}^{k_{n}}$

Тесты значимости для отклонения

Отклонение тестирования от HWP обычно выполняется с использованием теста хи-квадрата Пирсона , используя наблюдаемые частоты генотипа, полученные из данных, и ожидаемые частоты генотипа, полученные с использованием HWP. Для систем, в которых существует большое количество аллелей, это может привести к данным с множеством пустых возможных генотипов и низким уровнем генотипа, потому что в выборке часто не хватает людей, чтобы адекватно представлять все классы генотипа. Если это так, то асимптотическое предположение о распределении хи-квадрат , больше не будет удерживать, и может потребоваться использование формы точного теста Фишера , который требует компьютер решать ряд методов тестирования . Совсем недавно был предложен на отклонений от HWP (Guo & Thompson, 1992; Wigginton et al. 2005)

Пример тест хи-квадрат для отклонения

Эти данные взяты из EB Ford (1971) на алой тигровой моли , для которой были зарегистрированы фенотипы выборки популяции. Предполагается, что различие генотипа -фенотипа является незначительным. Нулевая гипотеза заключается в том, что население находится в пропорциях Харди -Вейнберга, и альтернативная гипотеза заключается в том, что население не в пропорциях Харди -Вайнберга.

Таблица 3: Пример принципа примера Харди -Вайнберга

Фенотип	Белые уколы (AA)	Промежуточный (AA)	Маленькое обнаружение (АА)	Общий
Число	1469	138	5	1612

Из этого можно рассчитать частоты аллеля:

${\begin{aligned}p&={2\times \mathrm {obs} ({\text{AA}})+\mathrm {obs} ({\text{Aa}}) \over 2\times (\mathrm {obs} ({\text{AA}})+\mathrm {obs} ({\text{Aa}})+\mathrm {obs} ({\text{aa}}))}\\\\&={2\times 1469+138 \over 2\times (1469+138+5)}\\\\&={3076 \over 3224}\\\\&=0.954\end{aligned}}$

и

${\begin{aligned}q&=1-p\\&=1-0.954\\&=0.046\end{aligned}}$

Итак, выносливо -Вейнберг Ожидается :

${\begin{aligned}\mathrm {Exp} ({\text{AA}})&=p^{2}n=0.954^{2}\times 1612=1467.4\\\mathrm {Exp} ({\text{Aa}})&=2pqn=2\times 0.954\times 0.046\times 1612=141.2\\\mathrm {Exp} ({\text{aa}})&=q^{2}n=0.046^{2}\times 1612=3.4\end{aligned}}$

Тест на хи-квадрат Пирсона гласит:

${\begin{aligned}\chi ^{2}&=\sum {(O-E)^{2} \over E}\\&={(1469-1467.4)^{2} \over 1467.4}+{(138-141.2)^{2} \over 141.2}+{(5-3.4)^{2} \over 3.4}\\&=0.001+0.073+0.756\\&=0.83\end{aligned}}$

Существует 1 степень свободы (степени свободы для испытания пропорций Харди -Вейнберга - # генотипы - # аллели). 5% Уровень значимости для 1 градуса свободы составляет 3,84, и, поскольку χ ² Ценность меньше, чем эта, нулевая гипотеза о том, что популяция находится на частотах Харди -Вайнберга, не отклоняется.

Точный тест Фишера (вероятностный тест)

Точный тест Фишера может быть применен для тестирования для пропорций Харди -Вейнберга. Поскольку тест является условным на частотах аллелей, P и Q , проблему можно рассматривать как тестирование на соответствующее количество гетерозигот. Таким образом, гипотеза пропорций Харди -Вейнберга отклоняется, если количество гетерозигот слишком большое или слишком мало. Условные вероятности гетерозиготы, учитывая частоты аллелей, приведены в Emigh (1980) как

$\operatorname {prob} [n_{12}\mid n_{1}]={\frac {\binom {n}{n_{11},n_{12},n_{22}}}{\binom {2n}{n_{1},n_{2}}}}2^{n_{12}},$

где n ₁₁ , n ₁₂ , n ₂₂ являются наблюдаемыми числами трех генотипов: AA, AA и AA, соответственно, а N ₁ - это число аллелей, где $n_{1}=2n_{11}+n_{12}$.

Пример Используя один из примеров из Emigh (1980), Мы можем рассмотреть случай, где n = 100 и p = 0,34. Возможные наблюдаемые гетерозиготы и их точный уровень значимости приведены в таблице 4.

Таблица 4: Пример точного теста Фишера на n = 100, p = 0,34.

Количество гетерозигот	Уровень значимости
0	0.000
2	0.000
4	0.000
6	0.000
8	0.000
10	0.000
12	0.000
14	0.000
16	0.000
18	0.001
20	0.007
22	0.034
34	0.067
24	0.151
32	0.291
26	0.474
30	0.730
28	1.000

Используя эту таблицу, необходимо найти уровень значимости теста на основе наблюдаемого количества гетерозигот. Например, если один наблюдал 20 гетерозигот, уровень значимости для теста составляет 0,007. Как типично для точного теста Фишера для небольших образцов, градация уровней значимости довольно грубая.

Тем не менее, такая таблица должна быть создана для каждого эксперимента, поскольку таблицы зависят как от N так и от P. ,

Эквивалентные тесты

Тесты эквивалентности разработаны для того, чтобы установить достаточно хорошее согласие наблюдаемых частот генотипа и равновесия Харди Вайнберга. Позволять ${\mathcal {M}}$ Обозначите семейство распределений генотипов в предположении о равновесии Харди Вайнберга. Расстояние между распределением генотипа $p$ и равновесие Харди Вайнберга определяется $d(p,{\mathcal {M}})=\min _{q\in {\mathcal {M}}}d(p,q)$, где $d$ это какое -то расстояние. Проблема тестирования эквивалентности задается $H_{0}=\{d(p,{\mathcal {M}})\geq \varepsilon \}$ и $H_{1}=\{d(p,{\mathcal {M}})<\varepsilon \}$, где $\varepsilon >0$ это параметр толерантности. Если гипотеза $H_{0}$ Может быть отклонен, тогда популяция находится близко к равновесию Харди Вайнберга с высокой вероятностью. Тесты эквивалентности для биаллельного случая развиваются среди других в Wellek (2004). Тесты эквивалентности для случая нескольких аллелей предлагаются в Островском (2020).

Коэффициент инбридинга

Коэффициент инбридинга, $F$ (См. Также F -Статистика ), является одним из минус наблюдаемой частоты гетерозигот по сравнению с ожидаемым от уравновешивания Харди -Вайнберга.

$F={\frac {\operatorname {E} {(f({\text{Aa}}))}-\operatorname {O} (f({\text{Aa}}))}{\operatorname {E} (f({\text{Aa}}))}}=1-{\frac {\operatorname {O} (f({\text{Aa}}))}{\operatorname {E} (f({\text{Aa}}))}},$

где ожидаемое значение от равновесия Харди -Вайнберга дается

$\operatorname {E} (f({\text{Aa}}))=2pq$

Например, для данных Форда выше:

$F=1-{138 \over 141.2}=0.023.$

Для двух аллелей эквивалентен тесту на инбридинг, эквивалент теста на инбридинг $F=0$.

Коэффициент инбридинга нестабилен, поскольку ожидаемое значение приближается к нулю и, следовательно, не полезно для редких и очень распространенных аллелей. Для: $F{\big |}_{E=0,O=0}=-\infty$; $F{\big |}_{E=0,O>0}$ не определен.

История

Mendelian Genetics была заново открыта в 1900 году. Однако она оставалась несколько спорной в течение нескольких лет, так как тогда она не была известна, как это могло вызвать непрерывные характеристики. Удни Йул (1902) выступил против менделизма, потому что он думал, что доминирующие аллели будут расти среди населения. Американский отбора Уильям Э. Касл (1903) показал, что без частоты генотипа останутся стабильными. Карл Пирсон (1903) обнаружил одну позицию равновесия со значениями p = Q = 0,5. Реджинальд Паннетт , неспособный противостоять точке зрения Юля, представил проблему Г.Х. Харди , британскому математику , с которым он играл в крикет . Харди был чистым математиком и держал прикладную математику в некотором презрении; Его взгляд на использование биологов на математику встречается в его статье 1908 года, где он описывает это как «очень простое»:

Редактору науки: я неохотно вторжусь в дискуссию по вопросам, о которых у меня нет экспертных знаний, и я должен был ожидать очень простого момента, который я хотел бы, чтобы он был знаком биологам. Тем не менее, некоторые замечания г -на Удни Йуле, на что мистер Р.К. Паннетт привлек мое внимание, предполагают, что это все еще стоит сделать ...

Предположим, что АА является парой мендельских персонажей, доминирующим, и что в любом данном поколении количество чистых доминантов (AA), гетерозигот (AA) и чистых повторяющихся (AA) составляют P : 2 Q : r . Наконец, предположим, что цифры довольно большие, так что спаривание может рассматриваться как случайное, что полов равномерно распределены между тремя сортами и что все одинаково плодородны. Небольшой математики типа умноженного стола достаточно, чтобы показать, что в следующем поколении цифры будут как ( P + Q ) ² : 2 ( P + Q ) ( Q + R ) :( Q + R ) ² , или как P ₁ : 2 Q ₁ : R ₁ , скажем.

Интересный вопрос: в каких обстоятельствах это распределение будет таким же, как и в поколении? Легко увидеть, что условие для этого Q ² = пр . И с 1 _года. ² = p ₁ r ₁ , были значения P , Q R и какими бы ни , распределение в любом случае останется без изменений после второго поколения

Таким образом, этот принцип был известен как закон Харди в англоязычном мире до 1943 года, когда Курт Стерн указал, что он впервые был сформулирован независимо в 1908 году немецким врачом Вильгельмом Вайнбергом . Уильям Касл в 1903 году также получил соотношения для особого случая частот равных аллелей, и иногда это (но редко) называется законодательством Харди -Вейнберга -Каска.

Вывод уравнений Харди

Заявление Харди начинается с рецидива для частот P , 2 Q и r . Эти рецидивовые отношения следуют из фундаментальных концепций в вероятности, особенно независимости и условной вероятности . Например, рассмотрим вероятность потомства из поколения $\textstyle t$ быть гомозиготным доминирующим. Аллели унаследованы независимо от каждого родителя. Доминирующий аллель может быть унаследован от гомозиготного доминирующего родителя с вероятностью 1 или от гетерозиготного родителя с вероятностью 0,5. Чтобы представить эту рассуждения в уравнении, пусть $\textstyle A_{t}$ представляют наследование доминирующего аллеля от родителя. Кроме того, пусть $\textstyle AA_{t-1}$ и $\textstyle Aa_{t-1}$ Представляют потенциальные родительские генотипы в предыдущем поколении.

${\begin{aligned}p_{t}&=P(A_{t},A_{t})=P(A_{t})^{2}\\&=\left(P(A_{t}\mid AA_{t-1})P(AA_{t-1})+P(A_{t}\mid Aa_{t-1})P(Aa_{t-1})\right)^{2}\\&=\left((1)p_{t-1}+(0.5)2q_{t-1}\right)^{2}\\&=\left(p_{t-1}+q_{t-1}\right)^{2}\end{aligned}}$

То же самое рассуждения, применяемые к другим генотипам, дает два оставшихся рецидивовых отношения. Равновесие происходит, когда каждая пропорция постоянна между последующими поколениями. Более формально, население находится в равновесии в поколении $\textstyle t$ когда

$\textstyle 0=p_{t}-p_{t-1}$, $\textstyle 0=q_{t}-q_{t-1}$, и $\textstyle 0=r_{t}-r_{t-1}$

Благодаря решению этих уравнений, необходимых, и можно определить достаточные условия для равновесия. Опять же, рассмотрим частоту гомозиготных доминирующих животных. Равновесие подразумевает

${\begin{aligned}0&=p_{t}-p_{t-1}\\&=p_{t-1}^{2}+2p_{t-1}q_{t-1}+q_{t-1}^{2}-p_{t-1}\end{aligned}}$

Сначала рассмотрим случай, где $\textstyle p_{t-1}=0$и обратите внимание, что это подразумевает, что $\textstyle q_{t-1}=0$ и $\textstyle r_{t-1}=1$Полем Теперь рассмотрим оставшийся случай, где $\textstyle p_{t-1}\neq \textstyle 0$:

${\begin{aligned}0&=p_{t-1}(p_{t-1}+2q_{t-1}+q_{t-1}^{2}/p_{t-1}-1)\\&=q_{t-1}^{2}/p_{t-1}-r_{t-1}\end{aligned}}$

где окончательное равенство сохраняется, потому что пропорции аллеля должны суммироваться одному. В обоих случаях, $\textstyle q_{t-1}^{2}=p_{t-1}r_{t-1}$Полем Можно показать, что два других условия равновесия подразумевают одно и то же уравнение. Вместе растворы трех уравнений равновесия подразумевают достаточность состояния Харди для равновесия. Поскольку условие всегда сохраняется для второго поколения, все последующие поколения имеют одинаковые пропорции.

Числовой пример

Оценка распределения генотипа

Примером вычисления распределения генотипа, приведенное исходными уравнениями Харди, является поучительным. Распределение фенотипа из таблицы 3 выше будет использоваться для вычисления первоначального распределения генотипа Харди. Обратите внимание, что значения P и Q , используемые Hardy, не то же самое, что используются выше.

${\begin{aligned}{\text{sum}}&={\mathrm {obs} ({\text{AA}})+2\times \mathrm {obs} ({\text{Aa}})+\mathrm {obs} ({\text{aa}})}={1469+2\times 138+5}\\[5pt]&=1750\end{aligned}}$

${\begin{aligned}p&={1469 \over 1750}=0.83943\\[5pt]2q&={2\times 138 \over 1750}=0.15771\\[5pt]r&={5 \over 1750}=0.00286\end{aligned}}$

В качестве проверки на распределение вычислите

$p+2q+r=0.83943+0.15771+0.00286=1.00000\,$

и

$E_{0}=q^{2}-pr=0.00382.\,$

Для следующего поколения уравнения Харди дают

${\begin{aligned}q&={0.15771 \over 2}=0.07886\\\\p_{1}&=(p+q)^{2}=0.84325\\[5pt]2q_{1}&=2(p+q)(q+r)=0.15007\\[5pt]r_{1}&=(q+r)^{2}=0.00668.\end{aligned}}$

Снова, как проверяет распределение, вычислите

$p_{1}+2q_{1}+r_{1}=0.84325+0.15007+0.00668=1.00000\,$

и

$E_{1}=q_{1}^{2}-p_{1}r_{1}=0.00000\,$

которые являются ожидаемыми значениями. Читатель может продемонстрировать, что последующее использование значений второго поколения для третьего поколения даст идентичные результаты.

Оценка частоты носителей

Принцип Харди -Вайнберга также может быть использован для оценки частоты носителей аутосомно -рецессивного состояния в популяции, основанной на частоте страданий.

Давайте предположим $\textstyle {\frac {1}{2500}}$ Младенцы рождаются с муковисцидозом , речь идет о частоте гомозиготных людей, наблюдаемых в северной европейской популяции. Мы можем использовать уравнения Харди -Вайнберга для оценки частоты носителей, частоты гетерозиготных людей, $\textstyle 2pq$.

${\begin{aligned}&q^{2}={\frac {1}{2500}}\\[5pt]&q={\frac {1}{50}}\\[5pt]&p=1-q\end{aligned}}$

Как $\textstyle {\frac {1}{50}}$ маленький, мы можем взять П , $\textstyle 1-{\frac {1}{50}}$, чтобы быть 1.

${\begin{aligned}2pq=2\cdot {\frac {1}{50}}\\[5pt]2pq={\frac {1}{25}}\end{aligned}}$

Поэтому мы оцениваем скорость носителей $\textstyle {\frac {1}{25}}$, которая о частоте, наблюдаемой в северной европейской популяции.

Это может быть упрощено до частоты носителей, которая примерно вдвое превышает квадратный корень частоты рождения.

Графическое представление

Диаграмма De Finetti, представляющая распределение частот генотипа

Можно представлять распределение частот генотипа для биоаллельного локуса в популяции графически с использованием диаграммы De Finetti . В нем используется треугольный график (также известный как трилинейный, трехосный или тройной график ) представлять распределение трех частот генотипа по отношению друг к другу. Это отличается от многих других подобных графиков тем, что направление одной из оси было изменено. Изогнутая линия на диаграмме - парабола Харди -Вайнберг и представляет состояние, где аллели находятся в равновесии Харди -Вейнберга. Можно представлять влияние естественного отбора и его влияния на частоту аллелей на такие графики. Диаграмма De Finetti была разработана и широко использовалась AWF Edwards в его книге «Фонды математической генетики» .

Смотрите также

• F-статистика
• Индекс фиксации
• QST_ (генетика)
• Эффект Wahlund
• Регрессия к среднему
• Многономиальное распределение (Харди -Вайнберг является триномиальным распределением с вероятностями $(\theta ^{2},2\theta (1-\theta ),(1-\theta )^{2})$)
• Аддитивное неравновесное и z статистика
• Генетика популяции
• Генетическое разнообразие
• Эффект основателя
• Население узкого места
• Генетический дрейф
• Внедовая депрессия
• Коэффициент инбридинга
• Коэффициент отношений
• Естественный отбор
• Фитнес
• Генетическая нагрузка

Ссылки

Источники

• Замок, мы (1903). «Законы Гальтона и Менделя и некоторые законы, регулирующие улучшение рас в результате отбора». Труды Американской академии искусств и наук . 35 : 233–242.
• Кроу, JF (июль 1999 г.). «Харди, Вайнберг и языковые препятствия» . Генетика . 152 (3): 821–5. doi : 10.1093/Genetics/152.3.821 . ISSN   0016-6731 . PMC   1460671 . PMID   10388804 .
• Эдвардс, AWF 1977. Основы математической генетики. Издательство Кембриджского университета, Кембридж (2 -е изд., 2000). ISBN   0-521-775444-2
• Emigh, TH (1980). «Сравнение тестов на равновесие Харди - Вейнберг». Биометрия . 36 (4): 627–642. doi : 10.2307/2556115 . JSTOR   2556115 . PMID   25856832 .
• Ford, EB (1971). Экологическая генетика , Лондон.
• Го, SW; Томпсон, Элизабет А. (июнь 1992 г.). «Выполнение точного теста пропорции Харди -Вейнберга для нескольких аллелей». Биометрия . 48 (2): 361–72. doi : 10.2307/2532296 . ISSN   0006-341X . JSTOR   2532296 . PMID   1637966 .
• Харди, GH (июль 1908 г.). «Мендельские пропорции в смешанной популяции» (PDF) . Наука . 28 (706): 49–50. Bibcode : 1908sci .... 28 ... 49H . doi : 10.1126/science.28.706.49 . ISSN   0036-8075 . PMC   2582692 . PMID   17779291 .
• ИНЕЙХЕН, Роберт; Batschelet, Eduard (1975). «Генетический отбор и диаграммы де Финетти». Журнал математической биологии . 2 : 33–39. doi : 10.1007/bf00276014 . S2CID   123415153 .
• Масел, Джоанна (2012). «Переосмысление Харди -Вейнберга и генетического дрейфа в биологии бакалавриата». Биологии . 34 (8): 701–10. doi : 10.1002/bies.201100178 . PMID   22576789 . S2CID   28513167 .
• Пирсон, К. (1903). «Математический вклад в теорию эволюции. XI. О влиянии естественного отбора на изменчивость и корреляцию органов». Философские транзакции Королевского общества а . 200 (321–330): 1–66. Bibcode : 1903rspta.200 .... 1p . doi : 10.1098/rsta.1903.0001 .
• Стерн, С. (1943). «Закон Харди -Вейнберг». Наука . 97 (2510): 137–138. Bibcode : 1943sci .... 97..137S . doi : 10.1126/science.97.2510.137 . JSTOR   1670409 . PMID   17788516 .
• Вайнберг, У. (1908). «О доказательстве наследования у людей». Ежегодные выпуски Ассоциации патриотической естественной истории в Вюртемберге . 64 : 368–382.
• Виггинтон, JE; Катлер, DJ; Абекасис, гр (май 2005 г.). «Примечание о точных тестах равновесия Харди - Вейнберга» . Американский журнал человеческой генетики . 76 (5): 887–93. doi : 10.1086/429864 . ISSN   0002-9297 . PMC   1199378 . PMID   15789306 .
• Йул, Гу (1902). «Законы Менделя и их вероятное отношение к внутрирасовой наследственности» . Новый фитол . 1 (193–207): 222–238. doi : 10.1111/j.1469-8137.1902.tb07336.x .

Внешние ссылки

• Evolutionsolution (внизу страницы)
• Харди - Вейнбергский калькулятор равновесия
• Генетическая популяционная генетика симулятор
• Hardy C Внедрение Guo & Thompson 1992
• Исходный код (C/C ++/Fortran/R) для Wigginton et al. 2005
• Онлайн -генератор диаграммы де -финетти и тесты на равновесие Харди - Вайнберг
• Онлайн -тест на равновесие онлайн и рисунок диаграмм De Finetti Archived 26 мая 2015 года на машине Wayback
• Харди - Вейнбергский калькулятор равновесия