Геодезические на эллипсоиде

Геодезическая на сплюснутом эллипсоиде

Учение о геодезических на эллипсоиде возникло в связи с геодезией именно с решением сетей триангуляции . Фигура Земли хорошо аппроксимируется сплюснутым эллипсоидом , слегка приплюснутой сферой. Геодезическая – это кратчайший путь между двумя точками на искривленной поверхности, аналогичный прямой линии на плоской поверхности. Таким образом, решение триангуляционной сети на эллипсоиде представляет собой комплекс упражнений по сфероидальной тригонометрии ( Эйлер 1755 ).

Если Землю рассматривать как сферу , геодезические представляют собой большие круги (все из которых замкнуты), и проблемы сводятся к задачам сферической тригонометрии . Однако Ньютон (1687) показал, что под действием вращения Земли она напоминает слегка сплюснутый эллипсоид: в этом случае экватор и меридианы представляют собой единственные простые замкнутые геодезические. Более того, кратчайший путь между двумя точками на экваторе не обязательно проходит вдоль экватора. Наконец, если эллипсоид еще больше исказить и превратить в трехосный эллипсоид (с тремя различными полуосями), замкнутыми будут только три геодезические.

Геодезические на эллипсоиде вращения.

Существует несколько способов определения геодезических ( Hilbert & Cohn-Vossen 1952 , стр. 220–221 ). Простое определение: кратчайший путь между двумя точками на поверхности. Однако зачастую полезнее определять их как пути с нулевой геодезической кривизной , т. е. как аналог прямых на искривленной поверхности. Это определение охватывает геодезические, перемещающиеся по поверхности эллипсоида настолько далеко, что они начинают возвращаться к исходной точке, так что другие маршруты становятся более прямыми, и включает пути, которые пересекаются или повторяют сами себя. Достаточно короткие сегменты геодезической по-прежнему являются кратчайшим маршрутом между своими конечными точками, но геодезические не обязательно являются глобально минимальными (т.е. кратчайшими среди всех возможных путей). Каждый глобально кратчайший путь является геодезической, но не наоборот.

К концу XVIII века эллипсоид вращения (также используется термин сфероид ) был общепринятым приближением к фигуре Земли . Настройка сетей триангуляции повлекла за собой приведение всех измерений к эталонному эллипсоиду и решение полученной двумерной задачи в качестве упражнения по сфероидальной тригонометрии ( Бомфорд 1952 , глава 3) ( Лейк и др. 2015 , §4.5).

Рис. 1. Геодезическая AB на эллипсоиде вращения. N — северный полюс, а EFH находится на экваторе.

Различные геодезические задачи можно свести к одному из двух типов. Рассмотрим две точки: А на широте φ ₁ и долготе λ ₁ и Б на широте φ ₂ и долготе λ ₂ (см. рис. 1). Соединяющей геодезической (от A до B ) является AB длиной s ₁₂ , которая имеет азимуты α ₁ и α ₂ в двух конечных точках. Обычно рассматриваются две геодезические задачи:

1. прямая геодезическая задача или первая геодезическая задача , заданные A , α ₁ и s ₁₂ , определяют B и α ₂ ;
2. обратная геодезическая задача или вторая геодезическая задача , учитывая A и B , определяют s ₁₂ , α ₁ и α ₂ .

Как видно из рис. 1, эти задачи предполагают решение треугольника NAB по одному углу α ₁ для прямой задачи и λ ₁₂ = λ ₂ − λ ₁ для обратной задачи и двум его прилегающим сторонам.Для сферы решением этих задач являются простые упражнения сферической тригонометрии , решение которых дается формулами решения сферического треугольника . (См. статью о навигации по большому кругу .)

Для эллипсоида вращения характеристическая константа, определяющая геодезическую, была найдена Клеро (1735) . Систематическое решение путей геодезических было дано Лежандром (1806 г.) и Ориани (1806 г.) (и последующими статьями 1808 и 1810 гг .).Полное решение прямой задачи (вместе с расчетными таблицами и разработанным примером) дано Бесселем (1825) .

В XVIII веке геодезические линии обычно назывались «кратчайшими линиями».Термин «геодезическая линия» (собственно, кривая ) был введен Лапласом (1799b) :

мы назовем геодезической Эту линию .

Эта терминология была введена в английский язык либо как «геодезическая линия», либо как «геодезическая линия», например ( Hutton 1811 , стр. 115 ),

Линия, прочерченная тем способом, который мы сейчас описали, или выведенная из тригонометрических мер указанными нами средствами, называется геодезической или геодезической линией: она обладает свойством быть кратчайшей, которую можно провести между двумя ее концами на поверхность Земли; и поэтому это правильная маршрутная мера расстояния между этими двумя пунктами.

При его принятии в других областях геодезической линии , часто сокращаемой до геодезической предпочтение отдавалось .

В этом разделе рассматривается задача об эллипсоиде вращения (как сплюснутом, так и вытянутом). Задача о трехосном эллипсоиде рассматривается в следующем разделе.

Уравнения геодезической

Рис. 2. Дифференциальный элемент меридионального эллипса.

Рис. 3. Дифференциальный элемент геодезической на эллипсоиде.

Здесь разрабатываются уравнения геодезической; этот вывод очень похож на вывод Бесселя (1825 г.) . Джордан и Эггерт (1941) , Багратуни (1962 , §15), Ганьшин (1967 , гл. 5), Кракивский и Томсон (1974 , §4), Рапп (1993 , §1.2), Джекели (2012) и Борре и Странг (2012) также приводят вывод этих уравнений.

Рассмотрим эллипсоид вращения с экваториальным радиусом a и полярной полуосью b . Определим сплющивание f , эксцентриситет e и второй эксцентриситет e ′ :

$f={\frac {a-b}{a}},\quad e={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\sqrt {f(2-f)}},\quad e'={\frac {\sqrt {a^{2}-b^{2}}}{b}}={\frac {e}{1-f}}.$

(В большинстве приложений в геодезии эллипсоид считается сплюснутым, a > b ; однако теория без изменений применима к вытянутым эллипсоидам, a < b , и в этом случае f , e ² , и е ′ ² отрицательные.)

Пусть элементарный отрезок пути на эллипсоиде имеет длину ds . Из рис. 2 и 3, мы видим, что если его азимут равен α , то ds связано с dφ и dλ соотношением

$\cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,$ (1)

где ρ — меридиональный радиус кривизны , R = ν cos φ — радиус круга широты φ , а ν — нормальный радиус кривизны .Таким образом, элементарный сегмент определяется выражением

$ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}$

или

${\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}$

где φ ′ = dφ / dλ и функция Лагранжа L зависит от φ через ρ( φ ) и R ( φ ) . Длина произвольного пути между ( φ ₁ , λ ₁ ) и ( φ ₂ , λ ₂ ) определяется выражением

$s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,$

где φ — функция от λ, удовлетворяющая φ ( λ ₁ ) = φ ₁ и φ ( λ ₂ ) = φ ₂ . Кратчайший путь или геодезическая влечет за собой нахождение той функции φ ( λ ), которая минимизирует s ₁₂ . Это упражнение в вариационном исчислении , а условие минимизации задается тождеством Бельтрами :

$L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}$

Подставив L и используя уравнения. (1) дает

$R\sin \alpha ={\text{const.}}$

Клеро (1735) нашел это соотношение , используя геометрическую конструкцию; аналогичный вывод представлен Люстерником (1964 , §10). Дифференцирование этого отношения дает

$d\alpha =\sin \varphi \,d\lambda .$

Это вместе с уравнениями (1) , приводит к системе обыкновенных дифференциальных уравнений для геодезической

${\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.$

Мы можем выразить R через широту параметрическую β , используя

$R=a\cos \beta ,$

и соотношение Клеро тогда становится

$\sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.$

Рис. 4. Геодезическая задача, отображенная на вспомогательную сферу.

Рис. 5. Элементарная задача геодезии на вспомогательной сфере.

Это правило синуса сферической тригонометрии, связывающее две стороны треугольника NAB (см. рис. 4), NA = 1 ⁄ 2 π − β ₁ и NB = 1 ⁄ 2 π - β ₂ и противоположные им углы B знак равно π - α ₂ и A = α ₁ .

Чтобы найти соотношение для третьей стороны AB = σ ₁₂ , длины сферической дуги , и угла N = ω ₁₂ , сферической долготы , полезно рассмотреть треугольник NEP, представляющий геодезическую, начинающуюся с экватора; см. рис. 5. На этом рисунке переменные, относящиеся к вспомогательной сфере, показаны, а соответствующие величины для эллипсоида указаны в скобках.Величины без индексов относятся к произвольной точке P ; E , точка, в которой геодезическая пересекает экватор в направлении на север, используется в качестве начала координат для σ , s и ω .

Рис. 6. Дифференциальный элемент геодезической на сфере.

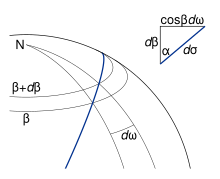
сторону EP Если расширить бесконечно малым перемещением P (см. рис. 6), получим

$\cos \alpha \,d\sigma =d\beta ,\quad \sin \alpha \,d\sigma =\cos \beta \,d\omega .$ (2)

Объединение уравнений. (1) и (2) дают дифференциальные уравнения для s и λ

${\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\frac {\sin \beta }{\sin \varphi }}.$

Связь между β и φ такова:

$\tan \beta ={\sqrt {1-e^{2}}}\tan \varphi =(1-f)\tan \varphi ,$

что дает

${\frac {\sin \beta }{\sin \varphi }}={\sqrt {1-e^{2}\cos ^{2}\beta }},$

так что дифференциальные уравнения геодезической принимают вид

${\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\sqrt {1-e^{2}\cos ^{2}\beta }}.$

Последний шаг — использовать σ в качестве независимого параметра в обоих этих дифференциальных уравнениях и тем самым выразить s и λ как интегралы. Применение правила синусов к вершинам E и G сферического треугольника EGP на рис. 5 дает

$\sin \beta =\sin \beta (\sigma ;\alpha _{0})=\cos \alpha _{0}\sin \sigma ,$

где α ₀ — азимут на E .Подставив это в уравнение для ds / d σ и проинтегрировав результат, получим

${\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',$ (3)

где

$k=e'\cos \alpha _{0},$

а пределы интеграла выбраны так, что s ( σ = 0) = 0 . Лежандр (1811 , стр. 180 ) указывал, что уравнение для s такое же, как уравнение для дуги эллипса с полуосями b √ 1 + e ′ ² потому что ² α ₀ и б . Чтобы выразить уравнение для λ через σ , запишем

$d\omega ={\frac {\sin \alpha _{0}}{\cos ^{2}\beta }}\,d\sigma ,$

что следует из уравнения 2 и соотношение Клеро.Это дает

$\lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',$ (4)

а пределы на интегралы выбраны так, что λ = λ ₀ при пересечении экватора, σ = 0 .

На этом решение пути геодезической с помощью вспомогательной сферы завершено. С помощью этого устройства большой круг можно точно отобразить на геодезической линии эллипсоида вращения.

Существует также несколько способов аппроксимации геодезических на земном эллипсоиде (с небольшим уплощением) ( Рапп 1991 , §6); некоторые из них описаны в статье о географическом расстоянии . Однако по сложности они обычно сравнимы с методом точного решения ( Jekeli 2012 , §2.1.4).

Поведение геодезических

Рис. 7. Меридианы и экватор — единственные замкнутые геодезические. (Для сильно уплощенных эллипсоидов существуют и другие замкнутые геодезические; см. рис. 11 и 12).

Геодезическая на сплюснутом эллипсоиде ( f = 1 ⁄ 50 ) с α ₀ = 45° .

Рис. 8. Проход по геодезической на эллипсоиде около 5 витков.

Рис. 9. Та же геодезическая примерно через 70 обходов.

Рис. 10. Геодезическая на вытянутом эллипсоиде ( f = − 1 ⁄ 50 ) с α ₀ = 45° . Сравните с рис. 8.

На рис. 7 показаны простые замкнутые геодезические, состоящие из меридианов (зеленый) и экватора (красный). (Здесь определение «простой» означает, что геодезическая замыкается сама на себя без промежуточного самопересечения.) Это следует из уравнений геодезических, приведенных в предыдущем разделе.

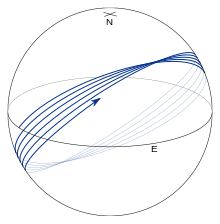
Все остальные геодезические характеризуются рис. 8 и 9, на которых показана геодезическая, начинающаяся на экваторе с углом α ₀ = 45° . Геодезическая колеблется вокруг экватора. Экваториальные пересечения называются узлами , а точки максимальной или минимальной широты — вершинами ; параметрические широты вершин определяются выражением β = ±( 1 ⁄ 2 π - |α ₀ |) . Геодезическая совершает одно полное колебание по широте до того, как долгота увеличится на 360° . Таким образом, при каждом последующем пересечении экватора на север (см. рис. 8) λ отстает от полного обхода экватора примерно на 2 π f sinα ₀ (для вытянутого эллипсоида эта величина отрицательна и λ завершает более чем полную схему см. рис. 10). Почти для всех значений α ₀ геодезическая заполнит ту часть эллипсоида между двумя широтами вершин (см. рис. 9).

Две дополнительные замкнутые геодезические для сплюснутого эллипсоида. b ⁄ a = 2 ⁄ 7 .

Рис. 11. Вид сбоку.

Рис. 12. Вид сверху.

Если эллипсоид достаточно сплюснут, т. е. б ⁄ а < 1 ⁄ 2 , возможен другой класс простых замкнутых геодезических ( Клингенберг 1982 , §3.5.19). Две такие геодезические показаны на рис. 11 и 12. Здесь b ⁄ a = 2 ⁄ 7 , а экваториальный азимут α ₀ для зеленой (соответственно синей) геодезической выбран равным 53,175° (соответственно 75,192° ), так что геодезическая совершает 2 (соответственно 3) полных колебания вокруг экватора на один контур эллипсоида.

Рис. 13. Геодезические (синие) из одной точки для f = 1 ⁄ 10 , φ ₁ = −30° ; геодезические круги показаны зеленым цветом, а разрез - красным.

На рис. 13 показаны геодезические линии (синим цветом), исходящие из A с α _1, кратным 15° , до точки, в которой они перестают быть кратчайшими путями. (Сглаживание было увеличено до 1 ⁄ 10 , чтобы подчеркнуть эллипсоидные эффекты.) Также показаны (зеленым цветом) кривые постоянной s ₁₂ , которые представляют собой геодезические круги с центром A . Гаусс (1828) показал, что на любой поверхности геодезические линии и геодезическая окружность пересекаются под прямым углом.

Красная линия — это разрезное геометрическое место , геометрическое место точек, которые имеют несколько (в данном случае две) кратчайших геодезических A. из На сфере разрез является точкой. На сплюснутом эллипсоиде (показанном здесь) это сегмент круга широты с центром в точке, A , противоположной φ = − φ ₁ . Протяженность разреза в продольном направлении составляет приблизительно λ ₁₂ ∈ [ π (1 − f cos φ ₁ ), π (1 + f cos φ ₁ )] . Если A лежит на экваторе, φ ₁ = 0 , это соотношение точное и, как следствие, экватор является кратчайшей геодезической, если | λ ₁₂ | ≤ π (1 - ж ) . Для вытянутого эллипсоида разрезом является отрезок антимеридиана с центром в точке, антиподальной к A , λ ₁₂ = π , и это означает, что меридиональные геодезические перестают быть кратчайшими путями до того, как будет достигнута антиподальная точка.

Дифференциальные свойства геодезических

Различные проблемы, связанные с геодезическими, требуют знания их поведения при возмущениях. Это полезно при тригонометрических корректировках ( Ehlert 1993 ), определении физических свойств сигналов, следующих за геодезическими, и т. д. Рассмотрим опорную геодезическую, параметризованную s , и вторую геодезическую, расположенную на небольшом расстоянии t ( s ) от нее. Гаусс (1828) показал, что t ( s ) подчиняется уравнению Гаусса-Якоби

${\frac {d^{2}t(s)}{ds^{2}}}+K(s)t(s)=0,$

Рис. 14. Определение приведенной длины и геодезического масштаба.

где K ( s ) — гауссова кривизна в точке s . Как линейное однородное дифференциальное уравнение второго порядка, его решение может быть выражено как сумма двух независимых решений.

$t(s_{2})=Cm(s_{1},s_{2})+DM(s_{1},s_{2})$

где

${\begin{aligned}m(s_{1},s_{1})&=0,\quad \left.{\frac {dm(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=1,\\M(s_{1},s_{1})&=1,\quad \left.{\frac {dM(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=0.\end{aligned}}$

Величина m ( s1 _собой , s2 ₎ = m12 _{представляет} так называемую длину , а ( s1 , _. s2 ) _{приведенную} = — _M12 геодезический масштаб M Их основные определения показаны на рис. 14.

Гауссова кривизна эллипсоида вращения равна

$K={\frac {1}{\rho \nu }}={\frac {{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}{b^{2}}}={\frac {b^{2}}{a^{4}{\bigl (}1-e^{2}\cos ^{2}\beta {\bigr )}^{2}}}.$

Гельмерт (1880 г. , уравнение (6.5.1.)) решил для этого случая уравнение Гаусса-Якоби, что позволило m ₁₂ и M ₁₂ выразить в виде интегралов.

Как видим из рис. 14 (верхний подрисунок), расстояние между двумя геодезическими, начинающимися в одной точке, с азимутами, отличающимися на d α _{1 ,} составляет m ₁₂ d α ₁ . На замкнутой поверхности, такой как эллипсоид, m ₁₂ колеблется около нуля. Точка, в которой m ₁₂ становится нулевой, является точкой, сопряженной с начальной точкой. Для того чтобы геодезическая между A и B длиной s12 _{была кратчайшим путем ,} она должна удовлетворять условию Якоби ( Якоби 1837 ) ( Якоби 1866 , §6) ( Форсайт 1927 , §§26–27) ( Блисс 1916) нет точки, сопряженной A. ), что между A и B с Если это условие не выполнено, то существует ближайший путь (не обязательно геодезический), который короче. Таким образом, условие Якоби является локальным свойством геодезической и является лишь необходимым условием того, что геодезическая является глобальной кратчайшей. Необходимыми и достаточными условиями того, что геодезическая является кратчайшим путем, являются:

• для сплюснутого эллипсоида, | σ ₁₂ | ≤ π ;
• для вытянутого эллипсоида, | λ ₁₂ | ≤ π , если α ₀ ≠ 0 ; если α ₀ = 0 , дополнительное условие m ₁₂ ≥ 0 требуется, если | λ ₁₂ | = π .

Конверт геодезических

Геодезические из одной точки ( f = 1 ⁄ 10 , φ ₁ = −30° )

Рис. 15. Огибающая геодезических из точки А при φ ₁ = −30° .

Рис. 16. Четыре геодезические, соединяющие А и точку В , φ ₂ = 26° , λ ₁₂ = 175° .

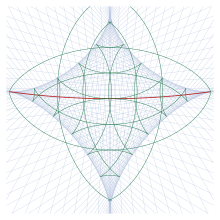
Геодезические из конкретной точки A, если продолжить их за разрез, образуют огибающую, показанную на рис. 15. Здесь геодезические, для которых α ₁ кратно 3 °, показаны голубым цветом. (Геодезические показаны только для первого прохождения вблизи точки противоположности, а не для последующих.) Некоторые геодезические круги показаны зеленым цветом; они образуют выступы на конверте. Локус разреза показан красным. Огибающая — это геометрическое место точек, сопряженных с A ; точки на огибающей можно вычислить, найдя точку на , в которой m ₁₂ = 0 геодезической . Якоби (1891) называет эту звездообразную фигуру, образуемую оболочкой, астроидой .

Вне астроиды в каждой точке пересекаются две геодезические; есть две геодезические (длиной примерно половина окружности эллипсоида) таким образом, между А и этими точками . Это соответствует ситуации на сфере, где существуют «короткие» и «длинные» маршруты по большому кругу между двумя точками. Внутри астроиды в каждой точке пересекаются четыре геодезические. Четыре таких геодезических показаны на рис. 16, где геодезические пронумерованы в порядке возрастания длины. (На этом рисунке используется то же положение А , что и на рис. 13, и он нарисован в той же проекции.) Две более короткие геодезические устойчивы , т. е. m ₁₂ > 0 , так что не существует ближайшего пути, соединяющего две точки, который был бы короче ; два других нестабильны. Только самая короткая линия (первая) имеет σ ₁₂ ≤ π . Все геодезические касаются оболочки, которая на рисунке показана зеленым цветом.

Астроида — это (внешняя) эволюта геодезических кругов с центром в A. точке Точно так же геодезические круги являются развертками астроиды.

Площадь геодезического многоугольника

См. Также: Равновеликая карта.

Геодезический многоугольник – это многоугольник, стороны которого являются геодезическими. Это аналог сферического многоугольника , стороны которого представляют собой большие круги. Площадь такого многоугольника можно найти, сначала вычислив площадь между геодезическим сегментом и экватором, т. е. площадь четырехугольника AFHB на рис. 1 ( Danielsen 1989 ). Как только эта площадь известна, площадь многоугольника можно вычислить путем суммирования вкладов всех краев многоугольника.

Здесь выражение для площади S ₁₂ AFHB Sjöberg разработано согласно (2006) . Площадь любой замкнутой области эллипсоида равна

$T=\int dT=\int {\frac {1}{K}}\cos \varphi \,d\varphi \,d\lambda ,$

где dT — элемент площади поверхности, а K — гауссова кривизна . Теперь теорема Гаусса – Бонне, примененная к состояниям геодезического многоугольника.

$\Gamma =\int K\,dT=\int \cos \varphi \,d\varphi \,d\lambda ,$

где

$\Gamma =2\pi -\sum _{j}\theta _{j}$

— геодезический эксцесс, а — _θj внешний угол в вершине j . Умножив уравнение для Γ на R ₂ ² , где R ₂ — аутентичный радиус , и вычитание его из уравнения для T дает

${\begin{aligned}T&=R_{2}^{2}\,\Gamma +\int \left({\frac {1}{K}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda \\&=R_{2}^{2}\,\Gamma +\int \left({\frac {b^{2}}{{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda ,\end{aligned}}$

где значение K для эллипсоида подставлено .Применяя эту формулу к четырехугольнику AFHB , отмечая, что Γ = α ₂ − α ₁ , и выполняя интеграл по φ, получаем

$S_{12}=R_{2}^{2}(\alpha _{2}-\alpha _{1})+b^{2}\int _{\lambda _{1}}^{\lambda _{2}}\left({\frac {1}{2{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}}}+{\frac {\tanh ^{-1}(e\sin \varphi )}{2e\sin \varphi }}-{\frac {R_{2}^{2}}{b^{2}}}\right)\sin \varphi \,d\lambda ,$

где интеграл ведется по геодезической линии (так что φ неявно является функцией λ ). Интеграл можно выразить как ряд, действительный для малых f ( Danielsen 1989 ) ( Karney 2013 , §6 и приложение).

Площадь геодезического многоугольника определяется суммированием S ₁₂ по его краям. Этот результат справедлив при условии, что многоугольник не содержит полюса; если да, то 2 π R ₂ ² необходимо добавить к сумме. Если ребра заданы своими вершинами, то удобным выражением для геодезического избытка E ₁₂ = α ₂ − α ₁ будет

$\tan {\frac {E_{12}}{2}}={\frac {\sin {\tfrac {1}{2}}(\beta _{2}+\beta _{1})}{\cos {\tfrac {1}{2}}(\beta _{2}-\beta _{1})}}\tan {\frac {\omega _{12}}{2}}.$

Решение прямой и обратной задач

Дополнительная информация: Географическое расстояние § Формулы эллипсоидальной поверхности.

Смотрите также: Азимут § В геодезии.

Решение геодезических задач влечет за собой отображение геодезической на вспомогательной сфере и решение соответствующей проблемы навигации по большому кругу .При решении «элементарного» сферического треугольника для NEP на рис. 5 правила Нейпира для квадрантных треугольников можно использовать :

${\begin{aligned}\sin \alpha _{0}&=\sin \alpha \cos \beta =\tan \omega \cot \sigma ,\\\cos \sigma &=\cos \beta \cos \omega =\tan \alpha _{0}\cot \alpha ,\\\cos \alpha &=\cos \omega \cos \alpha _{0}=\cot \sigma \tan \beta ,\\\sin \beta &=\cos \alpha _{0}\sin \sigma =\cot \alpha \tan \omega ,\\\sin \omega &=\sin \sigma \sin \alpha =\tan \beta \tan \alpha _{0}.\end{aligned}}$

Отображение геодезической включает в себя вычисление интегралов для расстояния s и долготы λ , уравнения. (3) и (4) и они зависят от параметра α ₀ .

Решение прямой задачи несложно, поскольку α ₀ можно определить непосредственно из заданных величин φ ₁ и α ₁ ; пример расчета см. в Karney (2013) .

В случае обратной задачи λ ₁₂ задано ; это нелегко связать с эквивалентным сферическим углом ω ₁₂ , поскольку α ₀ неизвестен. Таким образом, решение задачи требует, чтобы α ₀ было найдено итеративно ( нахождение корня ); см . в Karney (2013) подробности .

В геодезических приложениях, где f мало, интегралы обычно оцениваются как ряды ( Лежандр 1806 ) ( Ориани 1806 ) ( Бессель 1825 ) ( Хельмерт 1880 ) ( Рейнсфорд 1955 ) ( Рапп 1993 ). Для произвольного f интегралы (3) и (4) можно найти с помощью числовой квадратуры или выразив их через эллиптические интегралы ( Лежандр 1806 ) ( Кейли 1870 ) ( Карни 2024 ).

Винсенти (1975) предлагает решения прямых и обратных задач; они основаны на последовательном разложении, осуществляемом до третьего порядка при уплощении, и обеспечивают точность около 0,1 мм для эллипсоида WGS84 ; однако обратный метод не сходится почти в противоположных точках.

Карни (2013) продолжает расширение до шестого порядка, которого достаточно для обеспечения полной точности двойной точности для | ж | ≤ 1 ⁄ 50 и улучшает решение обратной задачи так, что оно сходится во всех случаях. Карни (2013 , приложение) расширяет метод, используя эллиптические интегралы, которые можно применять к эллипсоидам с произвольным уплощением.

Геодезические на трехосном эллипсоиде

Решение геодезической задачи для эллипсоида вращения математически просто: из-за симметрии геодезические имеют константу движения , определяемую соотношением Клеро, позволяющую свести задачу к квадратуре . К началу 19 века (благодаря работам Лежандра , Ориани , Бесселя и др.) сложилось полное понимание свойств геодезических на эллипсоиде вращения.

С другой стороны, геодезические на трехосном эллипсоиде (с тремя неравными осями) не имеют очевидной константы движения и, таким образом, представляли собой сложную нерешенную проблему в первой половине XIX века. В замечательной статье Якоби (1839) обнаружил константу движения, позволяющую свести и эту задачу к квадратуре ( Клингенберг 1982 , §3.5).

Система координат трехосного эллипсоида

См. Также: Геодезические координаты и Эллипсоидно-гармонические координаты.

Рис. 17. Трехосные эллипсоидные координаты.

Рассмотрим эллипсоид, определяемый формулой

$h={\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}+{\frac {Z^{2}}{c^{2}}}=1,$

где ( X , Y , Z ) — декартовы координаты с центром на эллипсоиде и, без ограничения общности, a ≥ b ≥ c > 0 . Якоби (1866 , §§26–27)использовали (трехосные) эллипсоидальные координаты (с трехосной эллипсоидной широтой и трехосной эллипсоидной долготой , β , ω ), определенные формулой

${\begin{aligned}X&=a\cos \omega {\frac {\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {a^{2}-c^{2}}}},\\Y&=b\cos \beta \sin \omega ,\\Z&=c\sin \beta {\frac {\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {a^{2}-c^{2}}}}.\end{aligned}}$

В пределе b → a для сплюснутого эллипсоида , β становится параметрической широтой поэтому использование символа β согласуется с предыдущими разделами. Однако ω отличается . от сферической долготы, определенной выше

Линии сетки постоянных β (синий цвет) и ω (зеленый цвет) показаны на рис. 17. Они представляют собой ортогональную систему координат: линии сетки пересекаются под прямым углом. Главные сечения эллипсоида, определяемые X = 0 и Z = 0, показаны красным. Третье главное сечение Y = 0 покрыто линиями β = ±90° и ω = 0° или ±180° . Эти линии встречаются в четырех точках шлангокабеля (две из которых видны на этом рисунке), где главные радиусы кривизны равны. Здесь и на других рисунках этого раздела параметры эллипсоида равны a : b : c = 1,01:1:0,8 , и он рассматривается в ортогональной проекции из точки выше φ = 40° , λ = 30° .

Линии сетки эллипсоидальных координат можно интерпретировать в трехразные способы:

1. Они представляют собой «линии кривизны» на эллипсоиде: они параллельны направлениям главной кривизны ( Монж, 1796 ).
2. Они также являются пересечениями эллипсоида с софокусными системами одно- и двухлистных гиперболоидов ( Дюпен 1813 , Часть 5 ).
3. Наконец, это геодезические эллипсы и гиперболы, определяемые с использованием двух соседних точек пуповины ( Гильберт и Кон-Фоссен 1952 , стр. 188 ). Например, линии постоянного β на рис. 17 могут быть созданы с помощью знакомой конструкции струны для эллипсов с концами струны, прикрепленными к двум точкам шлангокабеля.

Решение Якоби

Якоби показал, что уравнения геодезических, выраженные в эллипсоидальных координатах, разделимы. Вот как он рассказал о своем открытии своему другу и соседу Бесселю ( Якоби 1839 , Письмо Бесселю):

Позавчера я свел к квадратуре задачу о геодезических линиях на эллипсоиде с тремя неравными осями . Это самые простые формулы в мире, абелевы интегралы , которые становятся хорошо известными эллиптическими интегралами, если две оси считаются равными.

Кенигсберг , 28 декабря 38 г.

Решение, данное Якоби ( Якоби 1839 ) ( Якоби 1866 , §28), есть

${\begin{aligned}\delta &=\int {\frac {{\sqrt {b^{2}\sin ^{2}\beta +c^{2}\cos ^{2}\beta }}\,d\beta }{{\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {{\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta -\gamma }}}}\\[6pt]&\quad -\int {\frac {{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega }}\,d\omega }{{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {{\bigl (}a^{2}-b^{2}{\bigr )}\sin ^{2}\omega +\gamma }}}}.\end{aligned}}$

Как отмечает Якоби, «функция угла β равна функции угла ω . Эти две функции являются просто абелевыми интегралами...» две константы δ и γ В решении появляются . Обычно δ равно нулю, если нижние пределы интегралов считаются начальной точкой геодезической, а направление геодезической определяется γ . Однако для геодезических, начинающихся в точках пуповины, мы имеем γ = 0 , а δ определяет направление в точке пуповины.Константа γ может быть выражена как

$\gamma ={\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta \sin ^{2}\alpha -{\bigl (}a^{2}-b^{2}{\bigl )}\sin ^{2}\omega \cos ^{2}\alpha ,$

где α — угол, образуемый геодезической с линиями постоянной ω . В пределе b → a это сводится к sinα cos β = const. , знакомое соотношение Клеро. Вывод результата Якоби дан Дарбу (1894 , §§583–584 ); он дает решение, найденное Лиувиллем (1846 г.) для общих квадратичных поверхностей.

Съемка трехосных геодезических

Циркумполярные геодезические, ω ₁ = 0° , α ₁ = 90° .

Рис. 18. β ₁ = 45,1° .

Рис. 19. β ₁ = 87,48° .

На трехосном эллипсоиде есть только три простые замкнутые геодезические, три главных сечения эллипсоида, заданные X = 0 , Y = 0 и Z = 0 . Для съемки других геодезических удобно рассматривать геодезические, пересекающие среднее главное сечение Y = 0 под прямым углом. Такие геодезические показаны на рис. 18–22, где используются те же параметры эллипсоида и то же направление взгляда, что и на рис. 17. Кроме того, на каждом из этих рисунков красным показаны три главных эллипса.

Если отправной точкой является β ₁ ∈ (−90°, 90°) , ω ₁ = 0 и α ₁ = 90° , то γ > 0 и геодезическая окружает эллипсоид в «цирцимполярном» смысле. Геодезическая колеблется к северу и югу от экватора; при каждом колебании он совершает чуть меньше полного оборота вокруг эллипсоида, что в типичном случае приводит к заполнению геодезической области, ограниченной двумя линиями широты β = ± β ₁ . Два примера приведены на рис. 18 и 19. На рис. 18 показано практически то же поведение, что и для сплюснутого эллипсоида вращения (поскольку a ≈ b ); сравните с рис. 9.Однако если начальная точка находится на более высокой широте (рис. 18), то искажения, возникающие из-за a ≠ b, очевидны. Все касательные к циркумполярной геодезической касаются конфокального однополостного гиперболоида, который пересекает эллипсоид в точке β = β ₁ ( Chasles 1846 ) ( Hilbert & Cohn-Vossen 1952 , стр. 223–224 ).

Трансполярные геодезические, β ₁ = 90° , α ₁ = 180° .

Рис. 20. ω ₁ = 39,9° .

Рис. 21. ω ₁ = 9,966° .

Если начальной точкой является β ₁ = 90° , ω ₁ ∈ (0°, 180°) и α ₁ = 180° , то γ < 0 и геодезическая окружает эллипсоид в «трансполярном» смысле. Геодезическая колеблется к востоку и западу от эллипса X = 0 ; при каждом колебании он совершает чуть больше полного оборота вокруг эллипсоида. В типичном случае это приводит к заполнению геодезической областью, ограниченной двумя долготными линиями ω = ω ₁ и ω = 180° − ω ₁ .Если a = b , все меридианы являются геодезическими; эффект a ≠ b заставляет такие геодезические колебаться на восток и запад.Два примера приведены на рис. 20 и 21. Сужение геодезической вблизи полюса исчезает в пределе b → c ; в этом случае эллипсоид становится вытянутым эллипсоидом, и рис. 20 будет напоминать рис. 10 (повернутый набок). Все касательные к трансполярной геодезической касаются софокусного двуполостного гиперболоида, который пересекает эллипсоид в точке ω = ω ₁ .

Рис. 22. Умбиликальная геодезическая, β ₁ = 90° , ω ₁ = 0° , α ₁ = 135° .

Если начальная точка равна β ₁ = 90° , ω ₁ = 0° (точка пуповины) и α ₁ = 135° (геодезическая выходит из эллипса Y = 0 под прямым углом), то γ = 0 и геодезическая повторно пересекает противоположную точку пуповины и возвращается в исходную точку. Однако на каждом контуре угол, под которым она пересекает Y = 0, становится ближе к 0° или 180°, так что асимптотически геодезическая лежит на эллипсе Y = 0 ( Hart 1849 ) ( Arnold 1989 , стр. 265 ), как показано в Рис. 22. Одна геодезическая не заполняет область эллипсоида. Все касательные к омбилическим геодезическим касаются конфокальной гиперболы, пересекающей эллипсоид в омбилических точках.

Пупочные геодезические обладают несколькими интересными свойствами.

• Через любую точку эллипсоида проходят две пупочные геодезические.
• Геодезическое расстояние между противоположными пупочными точками одинаково независимо от начального направления геодезической.
• В то время как замкнутые геодезические на эллипсах X = 0 и Z = 0 устойчивы (геодезическая, изначально близкая к эллипсу и почти параллельная ему, остается близкой к эллипсу), замкнутая геодезическая на эллипсе Y = 0 , проходящая через все 4 точки пупка экспоненциально неустойчивы . Если его поколебать, он вылетит из плоскости Y = 0 и перевернется, прежде чем вернуться вплотную к плоскости. (Это поведение может повторяться в зависимости от природы начального возмущения.)

Если начальная точка A геодезической не является точкой пупка, ее оболочка представляет собой астроиду с двумя точками возврата, лежащими на β = − β ₁ , а двумя другими на ω = ω ₁ + π . Локус разреза для A — это часть линии β = − β ₁ между точками возврата.

Приложения

Прямая и обратная геодезические задачи больше не играют той центральной роли в геодезии, которую они играли когда-то. Вместо решения настройки геодезических сетей как двумерной задачи сфероидальной тригонометрии, эти проблемы теперь решаются трехмерными методами ( Винсенти и Боуринг 1978 ).Тем не менее, наземная геодезия по-прежнему играет важную роль в нескольких областях:

• для измерения расстояний и площадей в географических информационных системах ;
• определение морских границ ( UNCLOS 2006 );
• в правилах Федерального управления гражданской авиации по зональной навигации ( RNAV 2007 );
• метод измерения расстояний в Спортивном кодексе ФАИ ( ФАИ 2018 ).
• помочь мусульманам найти направление в сторону Мекки

По принципу наименьшего действия многие задачи физики можно сформулировать в виде вариационной задачи, аналогичной задаче геодезической. Действительно, геодезическая задача эквивалентна движению частицы, вынужденной двигаться по поверхности, но в остальном не подверженной никаким силам ( Лаплас 1799а ) ( Гильберт и Кон-Фоссен 1952 , стр. 222 ).По этой причине геодезические на простых поверхностях, таких как эллипсоиды вращения или трехосные эллипсоиды, часто используются в качестве «тестовых примеров» для изучения новых методов. Примеры включают в себя:

• развитие эллиптических интегралов ( Лежандр, 1811 ) и эллиптических функций ( Вейерштрасс, 1861 );
• развитие дифференциальной геометрии ( Гаусс 1828 ) ( Кристофель 1869 );
• методы решения систем дифференциальных уравнений заменой независимых переменных ( Якоби, 1839 );
• изучение каустики ( Якоби, 1891 );
• исследования числа и устойчивости периодических орбит ( Пуанкаре, 1905 );
• в пределе c → 0 геодезические на трехосном эллипсоиде сводятся к случаю динамического биллиарда ;
• расширения до произвольного числа измерений ( Кноррер, 1980 );
• геодезический поток на поверхности ( Бергер 2010 , гл. 12).

См. также

• Пути секции земли
• Фигура Земли
• Географическое расстояние
• Навигация по большому кругу
• Большой эллипс
• геодезический
• Геодезия
• Картографическая проекция
  • Картографическая проекция трехосного эллипсоида
• Меридианная дуга
• Румбовидная линия
• Формулы Винсенти

Ссылки

• Арнольд, VI (1989). Математические методы классической механики . Перевод Фогтманна К.; Вайнштейн, А. (2-е изд.). Спрингер-Верлаг. ISBN  978-0-387-96890-2 . ОСЛК   4037141 .
• Багратуни, Г. В. (1967) [1962]. Курс сфероидальной геодезии . дои : 10.5281/zenodo.32371 . OCLC   6150611 . Перевод с русского языка Курса сфероидной геодезии (Москва, 1962 г.) ВВС США ( FTD-MT-64-390 )
• Бергер, М. (2010). Геометрия раскрыта . Перевод Сенешала, Л. Дж. Спрингера. дои : 10.1007/978-3-540-70997-8 . ISBN  978-3-540-70996-1 .
• Бессель, Ф.В. (2010) [1825]. «Расчет долготы и широты по геодезическим измерениям». Астрономические Нахрихтен . 331 (8). Перевод Карни, CFF; Дикин, RE: 852–861. arXiv : 0908.1824 . Бибкод : 2010AN....331..852K . дои : 10.1002/asna.201011352 . S2CID   118760590 . Английский перевод Астрона. Нахр. 4 , 241–254 (1825) . Ошибка .
• Блисс, Джорджия (1916). «Условие Якоби для задач вариационного исчисления в параметрической форме» . Труды Американского математического общества . 17 (2): 195–206. дои : 10.1090/S0002-9947-1916-1501037-4 .
• Бомфорд, Г. (1952). Геодезия . Оксфорд: Кларендон. OCLC   1396190 .
• Борре, К.; Стрэнг, РГ (2012). «11. Геометрия эллипсоида» (PDF) . Алгоритмы глобального позиционирования . Уэлсли-Кембридж Пресс. ISBN  978-0-9802327-3-8 . OCLC   795014501 .
• Кэли, А. (1870). «О геодезических линиях на сплюснутом сфероиде» . Философский журнал . 4-я серия. 40 (268): 329–340. дои : 10.1080/14786447008640411 .
• Чарльз, М. (1846). «О геодезических линиях и линиях кривизны поверхностей второй степени» . Журнал чистой и прикладной математики (на французском языке). 11 :5–20. PDF .
• Кристоффель, Э. Б. (1869). «Общая теория геодезических треугольников» . Трактаты Королевской академии наук в Берлине (на немецком языке): 119–176.
• Клеро, AC (1735 г.). «Геометрическое определение перпендикуляра к меридиану, проведенного Жаком Кассини» . Мемуары Королевской академии наук Парижа 1733 г. (на французском языке): 406–416.
• Дэниэлсен, Дж. С. (1989). «Площадь под геодезией». Обзор опроса . 30 (232): 61–66. дои : 10.1179/003962689791474267 .
• Дарбу, Ж.Г. (1894). Уроки общей теории поверхностей [ Уроки общей теории поверхностей ] (на французском языке). Полет. 3. Париж: Готье-Виллар. OCLC   8566228 .
• Дюпен, ПКФ (1813). Développements de Géométrie [ Развития геометрии ] (на французском языке). Париж: Курьер. OCLC   560800801 .
• Элерт, Д. (1993). триангуляции Методы эллипсоидной (Технический отчет). Серия Б: Прикладная геодезия, выпуск № 292 (на немецком языке). Немецкая геодезическая комиссия . OCLC   257615376 .
• Эйлер, Л. (1755). «Элементы сфероидальной тригонометрии, взятые из метода максимумов и минимумов» . Мемуары Королевской академии наук Берлина 1753 г. (на французском языке). 9 : 258–293. Цифры .
• ФАИ (2018). «Раздел 8.2.3». Спортивный кодекс ФАИ (PDF) (Технический отчет). Лозанна, Швейцария: Международная авиационная федерация.
• Форсайт, Арканзас (1927). Вариационное исчисление . Кембриджский университет. Нажимать. ISBN  978-1-107-64083-2 . OCLC   250050479 .
• Ганьшин, В. В. (1969) [1967]. Геометрия земного эллипсоида . Перевод Уиллиса, Дж. М. Сент-Луис: Аэронавигационный картографический и информационный центр. дои : 10.5281/zenodo.32854 . OCLC   493553 . Перевод с русского языка Геометрия земного эллипсоида (Москва, 1967).
• Гаусс, CF (1902) [1828]. Общие исследования криволинейных поверхностей 1827 и 1825 годов . Перевод Морхеда, Дж. К.; Хилтебейтель, AM Принстонский университет. Либ. OCLC   7824448 . PDF . Английский перевод Disquisitiones Generales Circa Superficies Curvas (Дитерих, Геттинген, 1828 г.).
• Харт, А.С. (1849 г.). «Геометрическая демонстрация некоторых свойств геодезических линий» . Кембриджский и Дублинский математический журнал . 4 : 80–84.
• Гельмерт, Ф.Р. (1964) [1880]. Математические и физические теории высшей геодезии . Том 1. Сент-Луис: Центр аэронавигационных карт и информации. дои : 10.5281/zenodo.32050 . OCLC   17273288 . Английский перевод «Математических и физических теорий высшей геодезии» , Том 1 (Тойбнер, Лейпциг, 1880 г.).
• Гильберт, Д .; Кон-Воссен, С. (1952). Геометрия и воображение . Перевод Неменьи, П. Нью-Йорк: Челси. ISBN  9780828400879 . OCLC   301610346 .
• Хаттон, К. (1811). Курс математики в трех томах, составленный для использования Королевской военной академией . Том. 3. Лондон: ФК и Дж. Ривингтон. OCLC   18031510 .
• Якоби, CGJ (1837). «Теория вариационного исчисления и дифференциальных уравнений» . Журнал чистой и прикладной математики (на немецком языке). 1837 (17): 68–82. дои : 10.1515/crll.1837.17.68 . S2CID   119469290 .
• Якоби, CGJ (1839). «Заметка из геодезической об эллипсоиде и различные применения замечательной аналитической подстановки » . Журнал чистой и прикладной математики (на немецком языке). 1839 (19): 309–313. дои : 10.1515/crll.1839.19.309 . S2CID   121670851 . Письмо Бесселю , декабрь. 28, 1838 г. Французский перевод (1841 г.).
• Якоби, CGJ (2009) [1866]. А. Клебш (ред.). Лекции по динамике . Перевод Балагагадхарана К. Нью-Дели: Книжное агентство Индостан. ISBN  978-81-85931-91-3 . МР2569315   . OCLC   440645889 . Английский перевод «Лекций по динамике» (Реймер, Берлин, 1866 г.). Ошибка .
• Якоби, CGJ (1891). «О кривой, касающейся всех геодезических линий эллипсоида вращения, исходящих из точки» [Огибающая геодезических линий, исходящих из одной точки эллипсоида]. В KTW Weierstrass (ред.). Собрание сочинений Якоби (на немецком языке). Том 7. Берлин: Реймер. стр. 72–87. OCLC   630416023 . Оп. пост., выполнено FHA Wangerin . PDF .
• Джекели, К. (2012), Геометрические системы отсчета в геодезии , Университет штата Огайо, hdl : 1811/51274
• Джордан, В .; Эггерт, О. (1962) [1941]. Справочник по геодезии . Том. 3. Перевод Carta, MW Вашингтон, округ Колумбия: Армейская картографическая служба. Бибкод : 1962hage.book.....J . дои : 10.5281/zenodo.35316 . ОСЛК   34429043 . Английский перевод Handbuch der Vermessungskunde , 8-е издание (Мецлер, Штутгарт, 1941).
• Карни, CFF (2013). «Алгоритмы геодезических работ» . Журнал геодезии . 87 (1): 43–55. arXiv : 1109.4448 . Бибкод : 2013JGeod..87...43K . дои : 10.1007/s00190-012-0578-z . Дополнения .
• Карни, CFF (2015). «Географическая библиотека» . Версия 1.44.
• Карни, CFF (2024). «Геодезика на произвольном эллипсоиде вращения» . Журнал геодезии . 98 (1): 4:1–14. arXiv : 2208.00492 . дои : 10.1007/s00190-023-01813-2 .
• Клингенберг, WPA (1982). Риманова геометрия . де Грюйер. ISBN  978-3-11-008673-7 . МР   0666697 . OCLC   8476832 .
• Кнёррер, Х. (1980). «Геодезика на эллипсоиде». Математические изобретения . 59 (2): 119–143. Бибкод : 1980InMat..59..119K . дои : 10.1007/BF01390041 . S2CID   118792545 .
• Краковский, Э.Дж.; Томсон, Д.Б. (1974), Расчеты геодезического положения (PDF) , Кафедра геодезии и инженерной геоматики, Конспекты лекций, Фредериктон, Нью-Йорк: Univ. Нью-Брансуик, Bibcode : 1974gpc..book.....K
• Лаплас, PS (1829) [1799a]. «Книга 1, §8». . Трактат по небесной механике . Том. 1. Перевод Боудича, Н. Бостон: Хиллард, Грей, Литтл и Уилкинс. OCLC   1294937 .
• Лаплас, PS (1799b). Трактат ( по небесной механике на французском языке). Полет. 2. Париж: Крепле. п. 112. OCLC   25448952 .
• Лежандр, AM (1806 г.). «Анализ сфероидальных треугольников» . Mémoires de l'Institut National de France (на французском языке) (1-й семестр): 130–161.
• Лежандр, AM (1811 г.). Упражнения по интегральному исчислению с различными порядками трансцендентов и квадратурами [ Упражнения по интегральному исчислению ] (на французском языке). Париж: Курьер. OCLC   312469983 .
• Лейк, А.; Рапопорт, Л.; Татарников, Д. (2015). Спутниковая съемка GPS (4-е изд.). Уайли. ISBN  978-1-119-01828-5 .
• Лиувилл, Дж. (1846 г.). «О частных случаях, когда уравнения движения точечной частицы могут быть проинтегрированы» . Журнал чистой и прикладной математики (на французском языке). 11 : 345–378. PDF
• Lyusternik, L. (1964). Shortest Paths: Variational Problems . Popular Lectures in Mathematics. Vol. 13. Translated by Collins, P.; Brown, R. B. New York: Macmillan. MR  0178386 . OCLC  1048605 . Translation from Russian of Кратчайшие Линии: Вариационные Задачи (Moscow, 1955).
• Монж, Г. (1850) [1796]. «О линиях кривизны на поверхности эллипсоида». В Дж. Лиувилле (ред.). Применение анализа к геометрии (на французском языке) (5-е изд.). Париж: Бакалавр. стр. 139–160. ОСЛК   2829112 . ( Рис. 1–2 , Рис. 3–4 ). Издание 1796 года ( рис. 1–2 , рис. 3–4 ). PDF-фигуры .
• Национальная геодезическая служба (2012). «Геодезические утилиты: обратное и прямое» . Версия 3.0.
• Ньютон, И. (1848) [1687]. «Книга 3, Предложение 19, Задача 3» . Математические принципы натуральной философии . Перевод Мотта А. Нью-Йорк: Ади. стр. 405–409. Английский перевод Philosophiæ Naturalis Principia Mathematica . Liber Tertius, положение XIX. Проб. II. стр. 422–424 .
• Ориани, Б. (1806). «Элементы сфероидальной тригонометрии. Ч. 1» [Элементы сфероидальной тригонометрии]. Мемуары Итальянского национального института (на итальянском языке). 1 (1): 118–198.
• Ориани, Б. (1808). «Элементы сфероидальной тригонометрии. Ч. 2» [Элементы сфероидальной тригонометрии]. Мемуары Итальянского национального института (на итальянском языке). 2 (1): 1–58.
• Ориани, Б. (1810). «Элементы сфероидальной тригонометрии. Ч. 3» [Элементы сфероидальной тригонометрии]. Мемуары Итальянского национального института (на итальянском языке). 2 (2): 1–58.
• Пуанкаре, Х. (1905). «Sur les lignes géodésiques des Surfaces выпуклых» [Геодезические линии на выпуклых поверхностях]. Труды Американского математического общества (на французском языке). 6 (3): 237–274. дои : 10.2307/1986219 . JSTOR   1986219 .
• Рейнсфорд, Х.Ф. (1955). «Длинная геодезическая на эллипсоиде». Бюллетень геодезии . 37 (1): 12–22. Бибкод : 1955BGeod..29...12R . дои : 10.1007/BF02527187 . S2CID   122111614 .
• Рэпп, Р.Х. (1991), Геометрическая геодезия, часть I , Университет штата Огайо, hdl : 1811/24333
• Рэпп, Р.Х. (1993), Геометрическая геодезия, часть II , Университет штата Огайо, hdl : 1811/24409
• РНКВ (2007). «Приложение 2.». Заказ 8260.54A, Стандарт зональной навигации США (PDF) (Технический отчет). Вашингтон, округ Колумбия: Федеральное управление гражданской авиации США.
• Сьоберг, Л.Е. (2006). «Определение площадей на плоскости, сфере и эллипсоиде». Обзор опроса . 38 (301): 583–593. дои : 10.1179/003962606780732100 .
• ЮНКЛОС (2006). Руководство по техническим аспектам Конвенции Организации Объединенных Наций по морскому праву 1982 г. (PDF) (Технический отчет) (4-е изд.). Монако: Международное гидрографическое бюро. Архивировано из оригинала (PDF) 24 мая 2013 г. Проверено 15 августа 2013 г.
• Винсенти, Т. (1975). «Прямые и обратные решения геодезических на эллипсоиде с применением вложенных уравнений» (PDF) . Обзор опроса . 23 (176): 88–93. Бибкод : 1975SurRv..23...88V . дои : 10.1179/sre.1975.23.176.88 . Приложение: Обзор обзора 23 (180): 294 (1976).
• Винсент, Т .; Боуринг, БР (1978). Применение трехмерной геодезии для корректировки горизонтальных сетей (PDF) (Технический отчет). НОАА. НОС НГС-13.
• Вейерштрасс, KTW (1861 г.). «О геодезических линиях на трехосном эллипсоиде» [Геодезические линии на трехосном эллипсоиде]. Ежемесячные отчеты Королевской академии наук в Берлине (на немецком языке): 986–997.

Внешние ссылки

• Геодезическая онлайн-библиография книг и статей по геодезии на эллипсоидах.
• Тестовый набор для геодезических , набор из 500000 геодезических для эллипсоида WGS84, рассчитанный с использованием высокоточной арифметики.
• Инструмент NGS, реализующий Vincenty (1975) .
• geod(1) , справочная страница утилиты PROJ для геодезических расчетов.
• Реализация Karney в GeographicLib ( 2013) .
• Рисование геодезических на Google Maps.