Равновеликая проекция

В картографии эквивалентная равновеликая , аутентичная или проекция — это картографическая проекция , которая сохраняет относительную меру площади между любыми и всеми областями карты. Эквивалентные проекции широко используются для тематических карт, показывающих распределение сценариев, таких как население, распределение сельскохозяйственных угодий, лесные массивы и т. д., поскольку карта равной площади не меняет видимую плотность картируемого явления.
По Гаусса теореме Egregium проекция равной площади не может быть конформной . Это означает, что проекция равной площади неизбежно искажает формы. Даже если точка или точки, или путь или пути на карте могут не иметь искажений, чем больше площадь отображаемого региона, тем больше и очевиднее неизбежно становится искажение форм.

Описание
[ редактировать ]Чтобы картографическая проекция сферы была равновеликой, ее порождающие формулы должны удовлетворять условию типа Коши-Римана : [ 1 ]
где является постоянным по всей карте. Здесь, представляет широту; представляет долготу; и и - это проекционные (плоские) координаты для данного координатная пара.
Например, синусоидальная проекция — это очень простая проекция равной площади. Его производящие формулы:
где это радиус земного шара. Вычисление частных производных,
и так
с принимая значение константы .
Для равновеликой карты эллипсоида соответствующее дифференциальное условие, которое должно быть выполнено, следующее: [ 1 ]
где – эксцентриситет эллипсоида вращения.
Статистическая сетка
[ редактировать ]Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( апрель 2020 г. ) |
Термин «статистическая сетка» относится к дискретной сетке (глобальной или локальной) представления поверхности равной площади, используемой для визуализации данных , геокодирования и статистического пространственного анализа . [ 2 ] [ 3 ] [ 4 ] [ 5 ] [ 6 ]
Список равновеликих проекций
[ редактировать ]Вот некоторые проекции, сохраняющие площадь:
- Азимутальный
- Ламберта азимутально-равновеликий
- Вихель (псевдоазимутальный)
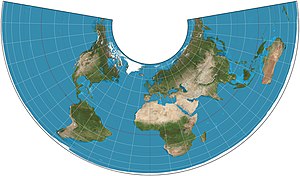
- Конический


- Цилиндрическая (с широтой без искажений)
- Ламбертовский цилиндрический равновеликий (0°)
- Берманн (30°)
- Хобо – Дайер (37 ° 30 ')
- Галл – Питерс (45 °)
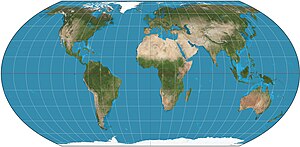
- Псевдоцилиндрический
- Другой
- Эккерт Грайфендорф
- Плоскополярная квартическая проекция Макбрайда-Томаса [ 7 ]
- Молоток
- Стремление 1995
- Равновеликая проекция Снайдера , используемая для геодезических сеток .
См. также
[ редактировать ]- Аутентичная широта
- Аутентичный радиус
- Равноплощадная карта (математика)
- Динамическая система, сохраняющая меру
- Площадь геодезического полигона
Ссылки
[ редактировать ]- ^ Jump up to: а б Снайдер, Джон П. (1987). Картографические проекции — Рабочее руководство . Профессиональная бумага USGS. Том. 1395. Вашингтон: Типография правительства США. п. 28. дои : 10.3133/pp1395 .
- ^ «Служба поддержки INSPIRE | INSPIRE» . Архивировано из оригинала 22 января 2021 года . Проверено 1 декабря 2019 г.
- ^ http://scorus.org/wp-content/uploads/2012/10/2010JurmalaP4.5.pdf. [ мертвая ссылка ]
- ^ БИГС (2016), «Статистическая сетка». Файл
grade_estatistica.pdfна FTP или HTTP, Censo 2010. Архивировано 2 декабря 2019 г. на Wayback Machine. - ^ Цулос, Лисандрос (2003). «Равноплощадная проекция для статистического картирования в ЕС» . В Аннони, Алессандро; Люзе, Клод; Гублер, Эрих (ред.). Картографические проекции Европы . Объединенный исследовательский центр Европейской комиссии. стр. 50–55.
- ^ Бродзик, Мэри Дж.; Биллингсли, Брендан; Харан, Терри; Рауп, Брюс; Савойя, Мэтью Х. (13 марта 2012 г.). «EASE-Grid 2.0: дополнительные, но значительные улучшения для наборов данных с привязкой к Земле» . Международный геоинформационный журнал ISPRS . 1 (1). МДПИ АГ: 32–45. дои : 10.3390/ijgi1010032 . ISSN 2220-9964 .
- ^ «Плоскополярная квартическая проекция Макбрайда-Томаса — MATLAB» . www.mathworks.com . Проверено 3 января 2024 г.













