Архимедова спираль

Спираль Архимеда (также известная как арифметическая спираль ) — это спираль жившего в III веке до нашей эры , названная в честь греческого математика Архимеда, . Это локус , соответствующий местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью . Эквивалентно, в полярных координатах $(r, θ)$ это можно описать уравнением

r=b\cdot \theta

с действительным числом

b

. Изменение параметра

b

управляет расстоянием между циклами.

Таким образом, из приведенного выше уравнения можно сказать: положение частицы от начальной точки пропорционально углу $θ$ с течением времени.

Архимед описал такую спираль в своей книге « О спиралях» . Конон Самосский был его другом, и Папп утверждает, что эту спираль открыл Конон. ^[1]

Вывод общего уравнения спирали [ править ]

Ниже используется физический подход для понимания понятия архимедовых спиралей.

Предположим, точечный объект движется в декартовой системе с постоянной скоростью $v$ , направленной параллельно $оси x$ , относительно $плоскости xy$ . Пусть в момент времени $t = 0$ объект находился в произвольной точке $(c, 0, 0)$ . Если $плоскость xy$ вращается с постоянной угловой скоростью $ω$ вокруг $оси z$ , то скорость точки относительно $оси z$ можно записать как:

{\begin{aligned}|v_{0}|&={\sqrt {v^{2}+\omega ^{2}(vt+c)^{2}}}\\v_{x}&=v\cos \omega t-\omega (vt+c)\sin \omega t\\v_{y}&=v\sin \omega t+\omega (vt+c)\cos \omega t\end{aligned}}

Как показано на рисунке рядом, у нас есть $vt + c$ , представляющий модуль вектора положения частицы в любой момент времени $t$ , с $v x$ и $v y$ в качестве компонентов скорости вдоль осей x и y соответственно.

{\begin{aligned}\int v_{x}\,dt&=x\\\int v_{y}\,dt&=y\end{aligned}}

Приведенные выше уравнения можно проинтегрировать, применив интегрирование по частям , что приводит к следующим параметрическим уравнениям:

{\begin{aligned}x&=(vt+c)\cos \omega t\\y&=(vt+c)\sin \omega t\end{aligned}}

Возведение двух уравнений в квадрат, а затем добавление (и некоторые небольшие изменения) приводит к декартову уравнению

{\sqrt {x^{2}+y^{2}}}={\frac {v}{\omega }}\cdot \arctan {\frac {y}{x}}+c

(используя тот факт, что

ωt = θ

и

θ = arctan .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}y / x

) или

\tan \left(\left({\sqrt {x^{2}+y^{2}}}-c\right)\cdot {\frac {\omega }{v}}\right)={\frac {y}{x}}

Его полярная форма

r={\frac {v}{\omega }}\cdot \theta +c.

Длина и кривизна дуги [ править ]

Учитывая параметризацию в декартовых координатах

f\colon \theta \mapsto (r\,\cos \theta ,r\,\sin \theta )=(b\,\theta \,\cos \theta ,b\,\theta \,\sin \theta )

дуги длина от

θ 1

до

θ 2

равна

{\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right]_{\theta _{1}}^{\theta _{2}}

или, что то же самое:

{\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\operatorname {arsinh} \theta \right]_{\theta _{1}}^{\theta _{2}}.

общая длина от

θ 1 = 0

до

θ 2 = θ

Таким образом, равна

{\frac {b}{2}}\left[\theta \,{\sqrt {1+\theta ^{2}}}+\ln \left(\theta +{\sqrt {1+\theta ^{2}}}\right)\right].

Кривизна определяется выражением

\kappa ={\frac {\theta ^{2}+2}{b\left(\theta ^{2}+1\right)^{\frac {3}{2}}}}

Характеристики [ править ]

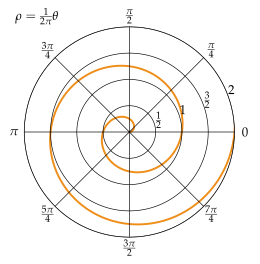
Спираль Архимеда обладает тем свойством, что любой луч из начала координат пересекает последовательные витки спирали в точках с постоянным расстоянием разделения (равным $2 πb$ , если $θ$ измеряется в радианах ), отсюда и название «арифметическая спираль». В отличие от этого в логарифмической спирали эти расстояния, а также расстояния точек пересечения, отсчитываемые от начала координат, образуют геометрическую прогрессию .

Спираль Архимеда имеет два рукава: один для $θ > 0$ и один для $θ < 0$ . Оба плеча плавно соединены в начале. На прилагаемом графике показана только одна рука. Если зеркально отобразить эту руку по $оси Y$ , получится другая рука.

При больших $θ$ точка движется с хорошо аппроксимированным равномерным ускорением вдоль спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью. ^[2] (см. вклад Михаила Гайченкова).

По мере роста архимедовой спирали ее эволюция асимптотически приближается к окружности радиусом $| в | / о$ .

Общая спираль Архимеда [ править ]

Иногда термин «спираль Архимеда» используется для обозначения более общей группы спиралей.

r=a+b\cdot \theta ^{\frac {1}{c}}.

Обычная спираль Архимеда возникает, когда $c = 1$ . Другие спирали, попадающие в эту группу, включают гиперболическую спираль ( $c = -1$ ), спираль Ферма ( $c = 2$ ) и литуус ( $c = -2$ ).

Приложения [ править ]

Один из методов квадратуры круга , предложенный Архимедом, использует спираль Архимеда. Архимед также показал, как с помощью спирали можно разделить угол на три части . Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах. ^[3]

Спираль Архимеда имеет множество практических применений. Спиральные компрессоры , используемые для сжатия газов, имеют роторы, которые могут быть изготовлены из двух чередующихся спиралей Архимеда, эвольвент круга одинакового размера, почти напоминающих спирали Архимеда. ^[4] или гибридные кривые.

Архимедовы спирали можно найти в спиральных антеннах , которые могут работать в широком диапазоне частот.

Витки часов пружин баланса и канавки очень ранних граммофонных пластинок образуют архимедовы спирали, делая канавки равномерно расположенными (хотя позже было введено переменное расстояние между дорожками, чтобы максимизировать количество музыки, которую можно было записать на пластинку). ^[5]

Попросить пациента нарисовать спираль Архимеда — это способ количественной оценки человеческого тремора ; эта информация помогает в диагностике неврологических заболеваний.

Архимедовы спирали также используются в проекционных системах цифровой обработки света (DLP), чтобы минимизировать « эффект радуги », создавая впечатление, будто несколько цветов отображаются одновременно, хотя на самом деле красный, зеленый и синий чередуются очень быстро. . ^[6] Кроме того, спирали Архимеда используются в пищевой микробиологии для количественного определения концентрации бактерий с помощью спирального планшета. ^[7]

Они также используются для моделирования узора, который возникает в рулоне бумаги или ленте постоянной толщины, обернутом вокруг цилиндра. ^[8]^[9]

Многие динамические спирали (такие как спираль Паркера солнечного ветра или узор колеса Екатерины ) являются архимедовыми. Например, звезда LL Пегаса демонстрирует примерную архимедову спираль в окружающих ее пылевых облаках, которые, как полагают, являются выброшенным веществом из звезды, которая была превращена в спираль другой звездой-компаньоном как часть двойной звездной системы. ^[10]

См. также [ править ]

Винт Архимеда – Механизм для откачки воды ^[11]
Спираль Ферма - спираль, охватывающая равную площадь за оборот.
Золотая спираль - Самоподобная кривая, связанная с золотым сечением.
Гиперболическая спираль - Спираль, асимптотическая прямой.
Список спиралей
Логарифмическая спираль – Самоподобная кривая роста
Спираль Теодора – многоугольная кривая, состоящая из прямоугольных треугольников.
Символ тройной спирали — различные символы с тройной вращательной симметрией.

Ссылки [ править ]

^ Балмер-Томас, Айвор . «Конон Самосский». Словарь научной биографии . Том. 3. п. 391.
^ Слоан, Нью-Джерси (ред.). «Последовательность A091154» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
^ Бойер, Карл Б. (1968). История математики . Принстон, Нью-Джерси: Издательство Принстонского университета. стр. 140–142. ISBN 0-691-02391-3 .
^ Саката, Хироцугу; Окуда, Масаюки. «Устройство для сжатия жидкости, имеющее коаксиальные спиральные элементы» . Проверено 25 ноября 2006 г.
^ Пенндорф, Рон. «Раннее развитие LP» . Архивировано из оригинала 5 ноября 2005 года . Проверено 25 ноября 2005 г. . См. отрывок о Variable Groove .
^ Баллоу, Глен (2008), Справочник для звукорежиссеров , CRC Press, стр. 1586, ISBN 9780240809694
^ Гилкрист, Дж. Э.; Кэмпбелл, Дж. Э.; Доннелли, CB; Пилер, Дж. Т.; Делани, Дж. М. (1973). «Метод определения бактерий на спиральных пластинах» . Прикладная микробиология . 25 (2): 244–52. дои : 10.1128/АЕМ.25.2.244-252.1973 . ПМК 380780 . ПМИД 4632851 .
^ Перессини, Тони (3 февраля 2009 г.). «Проблема Джоан с рулоном бумаги» (PDF) . Архивировано из оригинала (PDF) 3 ноября 2013 года . Проверено 6 октября 2014 г.
^ Уолзер, Х.; Хилтон, П.; Педерсен, Дж. (2000). Симметрия . Математическая ассоциация Америки. п. 27 . ISBN 9780883855324 . Проверено 6 октября 2014 г.
^ Ким, Хёсон; Трехо, Альфонсо; Лю, Шэн-Юань; Сахай, Рагвендра; Таам, Рональд Э.; Моррис, Марк Р.; Хирано, Наоми; Се, И-Та (март 2017 г.). «Крупномасштабная небулярная структура двойной сверхветра на эксцентричной орбите». Природная астрономия . 1 (3): 0060. arXiv : 1704.00449 . Бибкод : 2017НатАс...1Е..60К . дои : 10.1038/s41550-017-0060 . S2CID 119433782 .
^

Внешние ссылки [ править ]

[1] Балмер-Томас, Айвор . «Конон Самосский». Словарь научной биографии . Том. 3. п. 391.

[2] Слоан, Нью-Джерси (ред.). «Последовательность A091154» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

[boyer-3] Бойер, Карл Б. (1968). История математики . Принстон, Нью-Джерси: Издательство Принстонского университета. стр. 140–142. ISBN 0-691-02391-3 .

[4] Саката, Хироцугу; Окуда, Масаюки. «Устройство для сжатия жидкости, имеющее коаксиальные спиральные элементы» . Проверено 25 ноября 2006 г.

[5] Пенндорф, Рон. «Раннее развитие LP» . Архивировано из оригинала 5 ноября 2005 года . Проверено 25 ноября 2005 г. . См. отрывок о Variable Groove .

[6] Баллоу, Глен (2008), Справочник для звукорежиссеров , CRC Press, стр. 1586, ISBN 9780240809694

[7] Гилкрист, Дж. Э.; Кэмпбелл, Дж. Э.; Доннелли, CB; Пилер, Дж. Т.; Делани, Дж. М. (1973). «Метод определения бактерий на спиральных пластинах» . Прикладная микробиология . 25 (2): 244–52. дои : 10.1128/АЕМ.25.2.244-252.1973 . ПМК 380780 . ПМИД 4632851 .

[uiuc-8] Перессини, Тони (3 февраля 2009 г.). «Проблема Джоан с рулоном бумаги» (PDF) . Архивировано из оригинала (PDF) 3 ноября 2013 года . Проверено 6 октября 2014 г.

[google-9] Уолзер, Х.; Хилтон, П.; Педерсен, Дж. (2000). Симметрия . Математическая ассоциация Америки. п. 27 . ISBN 9780883855324 . Проверено 6 октября 2014 г.

[10] Ким, Хёсон; Трехо, Альфонсо; Лю, Шэн-Юань; Сахай, Рагвендра; Таам, Рональд Э.; Моррис, Марк Р.; Хирано, Наоми; Се, И-Та (март 2017 г.). «Крупномасштабная небулярная структура двойной сверхветра на эксцентричной орбите». Природная астрономия . 1 (3): 0060. arXiv : 1704.00449 . Бибкод : 2017НатАс...1Е..60К . дои : 10.1038/s41550-017-0060 . S2CID 119433782 .

[11] ^

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]