Функция ошибки

Не путать с функцией потери .

В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf , представляет собой функцию, определяемую как:

$$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t.$$

Функция ошибки
График функции ошибок
Общая информация
Общее определение	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t$
Области применения	Вероятность, термодинамика, цифровая связь
Домен, кодомен и изображение
Домен	$\mathbb {R}$
Изображение	$\left(-1,1\right)$
Основные характеристики
Паритет	Странный
Особенности
Корень	0
Производная	${\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}$
Первообразная	$\int \operatorname {erf} z\,dz=z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}+C$
Определение серии
Серия Тейлора	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}$

Некоторые авторы определяют $\operatorname {erf}$ без фактора $2/{\sqrt {\pi }}$. Этот неэлементарный интеграл представляет собой сигмовидную функцию, которая часто встречается в уравнениях вероятности , статистике и уравнениях в частных производных . Во многих из этих приложений аргументом функции является действительное число. Если аргумент функции вещественный, то и значение функции также вещественное.

В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y , которая обычно распределяется со средним значением 0 и стандартным отклонением. 1 / √ 2 , erf x — это вероятность того, что Y попадает в диапазон [− x , x ] .

Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как

$$\operatorname {erfc} z=1-\operatorname {erf} z,$$

и мнимая функция ошибок ( erfi ), определяемая как

$$\operatorname {erfi} z=-i\operatorname {erf} iz,$$

где я — мнимая единица .

Имя

Название «функция ошибки» и ее аббревиатура erf были предложены Дж. У. Л. Глейшером в 1871 году из-за ее связи с «теорией вероятностей, и особенно с теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона легкости» ошибок, плотность которых определяется выражением

$$f(x)=\left({\frac {c}{\pi }}\right)^{1/2}e^{-cx^{2}}$$

( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q , как:

$$\left({\frac {c}{\pi }}\right)^{\frac {1}{2}}\int _{p}^{q}e^{-cx^{2}}\,\mathrm {d} x={\tfrac {1}{2}}\left(\operatorname {erf} \left(q{\sqrt {c}}\right)-\operatorname {erf} \left(p{\sqrt {c}}\right)\right).$$

График функции ошибок Erf(z) в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

Приложения

Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, то erf ( a / σ √ 2 ) — это вероятность того, что ошибка одного измерения лежит между − a и + a , для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.

Функции ошибок и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности , когда граничные условия задаются ступенчатой ​​функцией Хевисайда .

Функция ошибок и ее аппроксимации могут использоваться для оценки результатов, которые справедливы с высокой или низкой вероятностью. Учитывая случайную величину X ~ Norm[ µ , σ ] (нормальное распределение со средним значением µ и стандартным отклонением σ ) и константу L > µ , это можно показать посредством интегрирования путем подстановки:

$${\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}$$

где A и B — некоторые числовые константы. Если L достаточно далеко от среднего значения, а именно µ − L ≥ σ √ ln k , то:

$$\Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}$$

поэтому вероятность стремится к 0 при k → ∞ .

Вероятность того, что X находится в интервале [ L _a , L _b ], может быть получена как

$${\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}$$

Свойства

Участки в сложной плоскости

Интегральная функция exp(− z ² )

Эрф З

Свойство erf (− z ) = −erf z означает, что функция ошибок является нечетной функцией . Это непосредственно следует из того, что подынтегральная функция e ^{− т 2} является четной функцией (первообразная четной функции, равная нулю в начале координат, является нечетной функцией и наоборот).

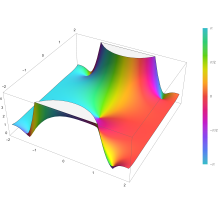
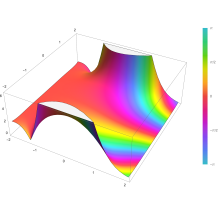
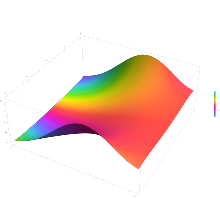
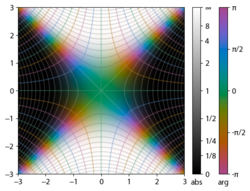
Поскольку функция ошибок представляет собой целую функцию , которая преобразует действительные числа в действительные числа, для любого комплексного числа z :

$$\operatorname {erf} {\overline {z}}={\overline {\operatorname {erf} z}}$$

где z — комплексно-сопряженное число z .

Подынтегральная функция f = exp(− z ² ) и f = erf z показаны на комплексной z -плоскости на рисунках справа с раскраской области .

Функция ошибок в точке +∞ равна ровно 1 (см. интеграл Гаусса ). На действительной оси erf z приближается к единице при z → +∞ и к −1 при z → −∞ . На мнимой оси оно стремится к ± i ∞ .

Серия Тейлора

Функция ошибки — это целая функция ; он не имеет особенностей (кроме точки на бесконечности), и его разложение Тейлора всегда сходится, но он широко известен «[...] своей плохой сходимостью, если x > 1 ».

Определяющий интеграл не может быть вычислен в замкнутом виде через элементарные функции (см. теорему Лиувилля ), а путем разложения подынтегральной функции e ^{- г 2} в ряд Маклорена и интегрируя почленно, можно получить ряд Маклорена функции ошибок как:

$${\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}$$

которое справедливо для любого комплексного числа   z . Членами знаменателя являются последовательность A007680 в OEIS .

Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:

$${\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}$$

потому что −(2 k − 1) z ² / k (2 k + 1) выражает множитель, превращающий k- й член в ( k + 1) -й член (считая z первым).

Функция мнимой ошибки имеет очень похожий ряд Маклорена:

$${\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}$$

которое справедливо для любого комплексного числа   z .

Производная и интеграл

Производная функции ошибок следует непосредственно из ее определения:

$${\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}.$$

Отсюда сразу же выводится и производная мнимой функции ошибок:

$${\frac {d}{dz}}\operatorname {erfi} z={\frac {2}{\sqrt {\pi }}}e^{z^{2}}.$$

Первообразная функции ошибок, получаемая интегрированием по частям , равна

$$z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.$$

Первообразная мнимой функции ошибок, которую также можно получить интегрированием по частям, равна

$$z\operatorname {erfi} z-{\frac {e^{z^{2}}}{\sqrt {\pi }}}.$$

Производные более высокого порядка имеют вид

$$\operatorname {erf} ^{(k)}z={\frac {2(-1)^{k-1}}{\sqrt {\pi }}}{\mathit {H}}_{k-1}(z)e^{-z^{2}}={\frac {2}{\sqrt {\pi }}}{\frac {\mathrm {d} ^{k-1}}{\mathrm {d} z^{k-1}}}\left(e^{-z^{2}}\right),\qquad k=1,2,\dots$$

где H физиков — полиномы Эрмита .

Серия Бюрмана

Расширение, которое сходится быстрее для всех действительных значений x , чем разложение Тейлора, получается с помощью Ганса Генриха Бюрмана : теоремы

$${\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}$$

где sn — знаковая функция . Оставив только первые два коэффициента и выбрав c ₁ = 31/200 ​ и = c ₂ − 341/8000 : , , полученное приближение показывает наибольшую относительную ошибку при x = ±1,3796 где она меньше 0,0036127

$$\operatorname {erf} x\approx {\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+{\frac {31}{200}}e^{-x^{2}}-{\frac {341}{8000}}e^{-2x^{2}}\right).$$

Обратные функции

Обратная функция ошибок

Учитывая комплексное число z , не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x < 1 существует уникальное действительное число, обозначаемое erf. ⁻¹ х удовлетворение

$$\operatorname {erf} \left(\operatorname {erf} ^{-1}x\right)=x.$$

Обратная функция ошибок обычно определяется в области (−1,1) и ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить и на диск | г | <1 комплексной плоскости с использованием ряда Маклорена

$$\operatorname {erf} ^{-1}z=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},$$

где c ₀ = 1 и

$${\begin{aligned}c_{k}&=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}\\[1ex]&=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},{\frac {34807}{16200}},\ldots \right\}.\end{aligned}}$$

Итак, мы имеем разложение в ряд (в числителях и знаменателях убраны общие множители):

$$\operatorname {erf} ^{-1}z={\frac {\sqrt {\pi }}{2}}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).$$

(После отмены дроби числителя/знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ±∞ равно ±1 .

Для | г | < 1 , мы имеем erf(erf ⁻¹ z ) знак равно z .

Обратная дополнительная функция ошибок определяется как

$$\operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}z.$$

Для действительного x существует уникальное действительное число erfi ⁻¹ x удовлетворяет erfi(erfi ⁻¹ Икс ) знак равно Икс . Обратная функция мнимой ошибки определяется как erfi ⁻¹ Икс .

Для любого действительного x метод Ньютона можно использовать для вычисления erfi. ⁻¹ x , а при −1 ≤ x ≤ 1 сходится следующий ряд Маклорена:

$$\operatorname {erfi} ^{-1}z=\sum _{k=0}^{\infty }{\frac {(-1)^{k}c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},$$

где c _k определяется, как указано выше.

Асимптотическое

Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :

$${\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}$$

где (2 n − 1)!! — двойной факториал числа (2 n − 1) , который является произведением всех нечётных чисел до (2 n − 1) . Этот ряд расходится для каждого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 имеет место

$$\operatorname {erfc} x={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}}+R_{N}(x)$$

где остаток

$$R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{1-2N}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,$$

что легко следует по индукции, записав

$$e^{-t^{2}}=-(2t)^{-1}\left(e^{-t^{2}}\right)'$$

и интегрируем по частям.

Асимптотическое поведение остаточного члена в обозначениях Ландау имеет вид

$$R_{N}(x)=O\left(x^{-(1+2N)}e^{-x^{2}}\right)$$

при Икс → ∞ . Это можно найти по

$$R_{N}(x)\propto \int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t=e^{-x^{2}}\int _{0}^{\infty }(t+x)^{-2N}e^{-t^{2}-2tx}\,\mathrm {d} t\leq e^{-x^{2}}\int _{0}^{\infty }x^{-2N}e^{-2tx}\,\mathrm {d} t\propto x^{-(1+2N)}e^{-x^{2}}.$$

Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения для получения хорошего приближения erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).

дроби

Разложение непрерывную дробь : дополнительной функции ошибки в

$$\operatorname {erfc} z={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {1}{z^{2}+{\cfrac {a_{1}}{1+{\cfrac {a_{2}}{z^{2}+{\cfrac {a_{3}}{1+\dotsb }}}}}}}},\qquad a_{m}={\frac {m}{2}}.$$

функции ошибок с функцией

$$\int _{-\infty }^{\infty }\operatorname {erf} \left(ax+b\right){\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x=\operatorname {erf} {\frac {a\mu +b}{\sqrt {1+2a^{2}\sigma ^{2}}}},\qquad a,b,\mu ,\sigma \in \mathbb {R}$$

что, по-видимому, связано с Нг и Геллером, формула 13 в разделе 4.3. с заменой переменных.

Факториальный ряд

Обратный факториальный ряд :

$${\begin{aligned}\operatorname {erfc} z&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}Q_{n}}{{\left(z^{2}+1\right)}^{\bar {n}}}}\\[1ex]&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\left[1-{\frac {1}{2}}{\frac {1}{(z^{2}+1)}}+{\frac {1}{4}}{\frac {1}{\left(z^{2}+1\right)\left(z^{2}+2\right)}}-\cdots \right]\end{aligned}}$$

сходится для Re( z ² ) > 0 . Здесь

$${\begin{aligned}Q_{n}&{\overset {\text{def}}{{}={}}}{\frac {1}{\Gamma {\left({\frac {1}{2}}\right)}}}\int _{0}^{\infty }\tau (\tau -1)\cdots (\tau -n+1)\tau ^{-{\frac {1}{2}}}e^{-\tau }\,d\tau \\[1ex]&=\sum _{k=0}^{n}\left({\frac {1}{2}}\right)^{\bar {k}}s(n,k),\end{aligned}}$$

С ^н обозначает возрастающий факториал , а s ( n , k ) обозначает знаковое число Стирлинга первого рода . Также существует представление бесконечной суммой, содержащей двойной факториал :

$$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-2)^{n}(2n-1)!!}{(2n+1)!}}z^{2n+1}$$

Численные аппроксимации

Приближение элементарными функциями

• Абрамовиц и Стегун дают несколько аппроксимаций различной точности (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке возрастания точности они следующие:
  $$\operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}\right)^{4}}},\qquad x\geq 0$$
  (максимальная ошибка: 5 × 10 ⁻⁴ )

  где а ₁ = 0,278393 , а ₂ = 0,230389 , а ₃ = 0,000972 , а ₄ = 0,078108

  $$\operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+a_{3}t^{3}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}},\qquad x\geq 0$$
  (максимальная ошибка: 2,5 × 10 ⁻⁵ )

  где p = 0,47047 , a ₁ = 0,3480242 , a ₂ = -0,0958798 , a ₃ = 0,7478556

  $$\operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6}\right)^{16}}},\qquad x\geq 0$$
  (максимальная ошибка: 3 × 10 ⁻⁷ )

  где a ₁ = 0,0705230784 , a ₂ = 0,0422820123 , a ₃ = 0,0092705272 , a ₄ = 0,0001520143 , a ₅ = 0,0002765672 , a ₆ = 0,0000430638

  $$\operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}}$$
  (максимальная ошибка: 1,5 × 10 ⁻⁷ )

  где p = 0,3275911 , a ₁ = 0,254829592 , a ₂ = -0,284496736 , a ₃ = 1,421413741 , a ₄ = -1,453152027 , a ₅ = 1,061405429

  Все эти приближения справедливы для x ≥ 0 . Чтобы использовать эти приближения для отрицательных x , используйте тот факт, что erf x является нечетной функцией, поэтому erf x = −erf(− x ) .

• Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок задаются выражением
  $${\begin{aligned}\operatorname {erfc} x&\leq {\frac {1}{2}}e^{-2x^{2}}+{\frac {1}{2}}e^{-x^{2}}\leq e^{-x^{2}},&\quad x&>0\\[1.5ex]\operatorname {erfc} x&\approx {\frac {1}{6}}e^{-x^{2}}+{\frac {1}{2}}e^{-{\frac {4}{3}}x^{2}},&\quad x&>0.\end{aligned}}$$
• Вышеупомянутое было обобщено на суммы N экспонент. с возрастающей точностью в терминах N , так что erfc x может быть точно аппроксимирован или ограничен 2 Q̃ ( √ 2 x ) , где
  $${\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.$$
  В частности, существует систематическая методология решения числовых коэффициентов {( a _n , b _n )} ^Н
  _{n = 1} , которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a _n , b _n )} ^Н
  _{n = 1} для многих вариантов экспоненциальных приближений и границы до N = 25 были выпущены в открытый доступ в виде комплексного набора данных.
• Точная аппроксимация дополнительной функции ошибок для x ∈ [0,∞) дана Карагианнидисом и Лиумпасом (2007). который показал при соответствующем выборе параметров { A , B } , что
  $$\operatorname {erfc} x\approx {\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi }}x}}.$$
  Они определили { A , B } = {1,98,1,135} , что дало хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
• Одночленная нижняя граница равна
  $$\operatorname {erfc} x\geq {\sqrt {\frac {2e}{\pi }}}{\frac {\sqrt {\beta -1}}{\beta }}e^{-\beta x^{2}},\qquad x\geq 0,\quad \beta >1,$$
  где параметр β можно выбрать так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
• Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
  $$\operatorname {erf} x\approx \operatorname {sgn} x\cdot {\sqrt {1-\exp \left(-x^{2}{\frac {{\frac {4}{\pi }}+ax^{2}}{1+ax^{2}}}\right)}}$$
  где
  $$a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.$$
  Это разработано так, чтобы быть очень точным в окрестности 0 и окрестности бесконечности, а относительная ошибка составляет менее 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.

  Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:

  $$\operatorname {erf} ^{-1}x\approx \operatorname {sgn} x\cdot {\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)^{2}-{\frac {\ln \left(1-x^{2}\right)}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)}}.$$

• Аппроксимация с максимальной погрешностью 1,2 × 10 ⁻⁷ для любого реального аргумента:
  $$\operatorname {erf} x={\begin{cases}1-\tau &x\geq 0\\\tau -1&x<0\end{cases}}$$
  с
  $${\begin{aligned}\tau &=t\cdot \exp \left(-x^{2}-1.26551223+1.00002368t+0.37409196t^{2}+0.09678418t^{3}-0.18628806t^{4}\right.\\&\left.\qquad \qquad \qquad +0.27886807t^{5}-1.13520398t^{6}+1.48851587t^{7}-0.82215223t^{8}+0.17087277t^{9}\right)\end{aligned}}$$
  и
  $$t={\frac {1}{1+{\frac {1}{2}}|x|}}.$$
• Приближение $\operatorname {erfc}$ с максимальной относительной погрешностью менее $2^{-53}$ $\left(\approx 1.1\times 10^{-16}\right)$ по абсолютной величине составляет: для $x\geq 0$,
  $${\begin{aligned}\operatorname {erfc} \left(x\right)&=\left({\frac {0.56418958354775629}{x+2.06955023132914151}}\right)\left({\frac {x^{2}+2.71078540045147805x+5.80755613130301624}{x^{2}+3.47954057099518960x+12.06166887286239555}}\right)\\&\left({\frac {x^{2}+3.47469513777439592x+12.07402036406381411}{x^{2}+3.72068443960225092x+8.44319781003968454}}\right)\left({\frac {x^{2}+4.00561509202259545x+9.30596659485887898}{x^{2}+3.90225704029924078x+6.36161630953880464}}\right)\\&\left({\frac {x^{2}+5.16722705817812584x+9.12661617673673262}{x^{2}+4.03296893109262491x+5.13578530585681539}}\right)\left({\frac {x^{2}+5.95908795446633271x+9.19435612886969243}{x^{2}+4.11240942957450885x+4.48640329523408675}}\right)e^{-x^{2}}\\\end{aligned}}$$
  и для $x<0$
  $$\operatorname {erfc} \left(x\right)=2-\operatorname {erfc} \left(-x\right)$$
• Простую аппроксимацию вещественных аргументов можно выполнить с помощью гиперболических функций :
  $$\operatorname {erf} \left(x\right)\approx z(x)=\tanh \left({\frac {2}{\sqrt {\pi }}}\left(x+{\frac {11}{123}}x^{3}\right)\right)$$
  который сохраняет абсолютную разницу $\left|\operatorname {erf} \left(x\right)-z(x)\right|<0.000358,\,\forall x$.

Таблица значений

Дополнительная информация: интервальная оценка , вероятность покрытия и правило 68–95–99,7.

Икс	двор х	1 − ярд х
0	0	1
0.02	0.022 564 575	0.977 435 425
0.04	0.045 111 106	0.954 888 894
0.06	0.067 621 594	0.932 378 406
0.08	0.090 078 126	0.909 921 874
0.1	0.112 462 916	0.887 537 084
0.2	0.222 702 589	0.777 297 411
0.3	0.328 626 759	0.671 373 241
0.4	0.428 392 355	0.571 607 645
0.5	0.520 499 878	0.479 500 122
0.6	0.603 856 091	0.396 143 909
0.7	0.677 801 194	0.322 198 806
0.8	0.742 100 965	0.257 899 035
0.9	0.796 908 212	0.203 091 788
1	0.842 700 793	0.157 299 207
1.1	0.880 205 070	0.119 794 930
1.2	0.910 313 978	0.089 686 022
1.3	0.934 007 945	0.065 992 055
1.4	0.952 285 120	0.047 714 880
1.5	0.966 105 146	0.033 894 854
1.6	0.976 348 383	0.023 651 617
1.7	0.983 790 459	0.016 209 541
1.8	0.989 090 502	0.010 909 498
1.9	0.992 790 429	0.007 209 571
2	0.995 322 265	0.004 677 735
2.1	0.997 020 533	0.002 979 467
2.2	0.998 137 154	0.001 862 846
2.3	0.998 856 823	0.001 143 177
2.4	0.999 311 486	0.000 688 514
2.5	0.999 593 048	0.000 406 952
3	0.999 977 910	0.000 022 090
3.5	0.999 999 257	0.000 000 743

Связанные функции

Дополнительная функция ошибок

Дополнительная функция ошибок , обозначаемая erfc , определяется как

График дополнительной функции ошибок Erfc(z) в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

$${\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}$$

который также определяет erfcx , масштабированную дополнительную функцию ошибок (который можно использовать вместо erfc, чтобы избежать арифметического опустошения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:

$$\operatorname {erfc} (x\mid x\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}\right)\,\mathrm {d} \theta .$$

Это выражение действительно только для положительных значений x , но его можно использовать в сочетании с erfc x = 2 − erfc(− x ) для получения erfc( x ) для отрицательных значений. Эта форма выгодна тем, что область интегрирования фиксирована и конечна. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:

$$\operatorname {erfc} (x+y\mid x,y\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}-{\frac {y^{2}}{\cos ^{2}\theta }}\right)\,\mathrm {d} \theta .$$

Функция мнимой ошибки

Мнимая функция ошибок , обозначаемая erfi , определяется как

График мнимой функции ошибок Erfi(z) в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

$${\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}$$

где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).

Несмотря на название «мнимая функция ошибки», erfi x действительна, когда x действительна.

Когда функция ошибок вычисляется для произвольных комплексных аргументов z , результирующая комплексная функция ошибок обычно рассматривается в масштабированной форме как функция Фаддеевой :

$$w(z)=e^{-z^{2}}\operatorname {erfc} (-iz)=\operatorname {erfcx} (-iz).$$

распределения

Функция ошибок по существу идентична стандартной нормальной функции кумулятивного распределения , обозначаемой Φ , также называемой нормой ( x ) в некоторых языках программирования. , поскольку они отличаются только масштабированием и переводом. Действительно,

нормальная кумулятивная функция распределения, построенная на комплексной плоскости

$${\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}$$

или переставить для erf и erfc :

$${\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}$$

Следовательно, функция ошибок также тесно связана с Q-функцией , которая представляет собой хвостовую вероятность стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как

$${\begin{aligned}Q(x)&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} {\frac {x}{\sqrt {2}}}\\&={\frac {1}{2}}\operatorname {erfc} {\frac {x}{\sqrt {2}}}.\end{aligned}}$$

Обратная функция Φ функция известна как нормальная функция квантиля или пробит- и может быть выражена через обратную функцию ошибок как

$$\operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\operatorname {erfc} ^{-1}(2p).$$

Стандартный нормальный CDF чаще используется в теории вероятности и статистике, а функция ошибок чаще используется в других разделах математики.

Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как вырожденная гипергеометрическая функция (функция Куммера):

$$\operatorname {erf} x={\frac {2x}{\sqrt {\pi }}}M\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).$$

Оно имеет простое выражение через интеграл Френеля .

В терминах регуляризованной гамма-функции P и -функции неполной гамма

$$\operatorname {erf} x=\operatorname {sgn} x\cdot P\left({\tfrac {1}{2}},x^{2}\right)={\frac {\operatorname {sgn} x}{\sqrt {\pi }}}\gamma {\left({\tfrac {1}{2}},x^{2}\right)}.$$

Sign x — знаковая функция .

Обобщенные функции ошибок

График обобщенных функций ошибок E _n ( x ) :

• серая кривая: E ₁ ( x ) = 1 - и ^{− х} / √ π
• красная кривая: E ₂ ( x ) = erf( x )
• зеленая кривая: E ₃ ( x )
• синяя кривая: E ₄ ( x )
• золотая кривая: E ₅ ( x ) .

Некоторые авторы обсуждают более общие функции:

$$E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}.$$

Известные случаи:

• E ₀ ( x ) — прямая линия, проходящая через начало координат: E ₀ ( x ) = х / е √ π
• E ₂ ( x ) — функция ошибок, erf x .

После деления на n ! , все En _n для нечетных выглядят похожими ( но не идентичными) друг другу. Аналогично, En _n для четных выглядят похожими (но не идентичными) друг другу после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне x графика.

Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :

$$E_{n}(x)={\frac {1}{\sqrt {\pi }}}\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right),\qquad x>0.$$

Следовательно, мы можем определить функцию ошибок через неполную гамма-функцию:

$$\operatorname {erf} x=1-{\frac {1}{\sqrt {\pi }}}\Gamma \left({\tfrac {1}{2}},x^{2}\right).$$

интегралы дополнительной

Повторные интегралы дополнительной функции ошибок определяются формулой

$${\begin{aligned}i^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }i^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]i^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\i^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\i^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}$$

Общая рекуррентная формула:

$$2n\cdot i^{n}\!\operatorname {erfc} z=i^{n-2}\!\operatorname {erfc} z-2z\cdot i^{n-1}\!\operatorname {erfc} z$$

У них есть степенной ряд

$$i^{n}\!\operatorname {erfc} z=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\,\Gamma \left(1+{\frac {n-j}{2}}\right)}},$$

откуда следуют свойства симметрии

$$i^{2m}\!\operatorname {erfc} (-z)=-i^{2m}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}$$

и

$$i^{2m+1}\!\operatorname {erfc} (-z)=i^{2m+1}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}.$$

Реализации

Как реальная функция реального аргумента

• В POSIX -совместимых операционных системах заголовок math.h объявит и математическую библиотеку libm должен обеспечивать функции erf и erfc ( двойная точность ), а также их с одинарной точностью и расширенной точностью. аналоги erff, erfl и erfcf, erfcl.
• GNU Научная библиотека предоставляет erf, erfc, log(erf)и масштабированные функции ошибок.

Как сложная функция сложного аргумента

• libcerf, числовая библиотека C для сложных функций ошибок, предоставляет сложные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью примерно 13–14 цифр, на основе функции Фаддеевой , реализованной в пакете MIT Faddeeva Package.
• Функцию для комплексных аргументов можно вычислить численно следующим образом:
  $$\operatorname {erf} \left(a+bi\right)={\frac {2}{\sqrt {\pi }}}e^{b^{2}}\int _{0}^{a}e^{-x^{2}}\cos \left(2bx\right)\,dx+i\left(\operatorname {erfi} \left(b\right)-{\frac {2}{\sqrt {\pi }}}e^{b^{2}}\int _{0}^{a}e^{-x^{2}}\sin \left(2bx\right)\,dx\right)$$

См. также

Связанные функции

• Интеграл Гаусса по всей действительной линии
• Функция Гаусса , производная
• Функция Доусона , перенормированная функция мнимой ошибки
• Интеграл Гудвина – Стейтона

Вероятно

• Нормальное распределение
• Нормальная кумулятивная функция распределения , масштабированная и сдвинутая форма функции ошибок.
• Пробит , обратная или квантильная функция нормального CDF.
• Q-функция , хвостовая вероятность нормального распределения
• Стандартная оценка

Дальнейшее чтение

• Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. п. 297. ИСБН  978-0-486-61272-0 . LCCN   64-60036 . МР   0167642 . LCCN   65-12253 .
• Пресс, Уильям Х.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8 , архивировано из оригинала 11 августа 2011 года , получено 9 августа 2011 года.
• Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля» , в Олвере, Фрэнке У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .

Внешние ссылки

• Таблица интегралов функций ошибок