Аэродинамика

«Аэродинамический» перенаправляется сюда. Чтобы узнать о других значениях, см. Аэродинамика (значения) .

Исследование НАСА турбулентности в следе на острове Уоллопс в 1990 году. Вихрь создается при прохождении крыла самолета, обнаруживаемый дымом. Вихри — одно из многих явлений, связанных с изучением аэродинамики.

Аэродинамика ( древнегреческий : ἀήρ aero (воздух) + древнегреческий : δυναμική (динамика)) — это изучение движения воздуха , особенно под воздействием твердого объекта, такого как крыло самолета . Он включает в себя темы, охватываемые областью гидродинамики и ее раздела газодинамики , и является важной областью исследований в области аэронавтики . Термин «аэродинамика» часто используется как синоним газовой динамики, с той разницей, что «газодинамика» применяется к изучению движения всех газов, а не ограничивается воздухом. Формальное изучение аэродинамики в современном смысле началось в восемнадцатом веке, хотя наблюдения за фундаментальными понятиями, такими как аэродинамическое сопротивление, были зафиксированы гораздо раньше. Большинство первых усилий в области аэродинамики были направлены на достижение полета тяжелее воздуха , что впервые было продемонстрировано Отто Лилиенталем в 1891 году. С тех пор использование аэродинамики посредством математического анализа, эмпирических приближений, экспериментов в аэродинамической трубе и компьютерного моделирования сформировало рациональную основу для развития полетов тяжелее воздуха и ряда других технологий. Недавние работы в области аэродинамики были сосредоточены на вопросах, связанных со сжимаемым потоком , турбулентностью и пограничными слоями , и носили все более вычислительный характер.

История

Основная статья: История аэродинамики

Современная аэродинамика возникла только в семнадцатом веке, но аэродинамические силы использовались людьми на протяжении тысячелетий в парусных лодках и ветряных мельницах. образы и рассказы о бегстве появляются на протяжении всей записанной истории, например, древнегреческая легенда об Икаре и Дедале . Фундаментальные понятия континуума , сопротивления и градиентов давления появляются в работах Аристотеля и Архимеда .

В 1726 году сэр Исаак Ньютон стал первым человеком, разработавшим теорию сопротивления воздуха. что сделало его одним из первых аэродинамиков. Голландско - швейцарский математик Даниэль Бернулли в 1738 году создал «Гидродинамику» , в которой описал фундаментальную взаимосвязь между давлением, плотностью и скоростью потока для несжимаемого потока, известную сегодня как принцип Бернулли , который обеспечивает один из методов расчета аэродинамической подъемной силы. В 1757 году Леонард Эйлер опубликовал более общие уравнения Эйлера , которые можно было применять как к сжимаемым, так и к несжимаемым потокам. Уравнения Эйлера были расширены, чтобы включить эффекты вязкости в первой половине 1800-х годов, что привело к уравнениям Навье-Стокса . Уравнения Навье – Стокса являются наиболее общими определяющими уравнениями потока жидкости, но их трудно решить для обтекания всех форм, кроме самых простых.

Копия Райт братьев аэродинамической трубы выставлена ​​в Центре авиации и космонавтики Вирджинии. Аэродинамические трубы сыграли ключевую роль в разработке и проверке законов аэродинамики.

В 1799 году сэр Джордж Кэли стал первым человеком, определившим четыре аэродинамические силы полета ( вес , подъемная сила , сопротивление и тяга ), а также взаимосвязь между ними. и тем самым наметил путь к достижению полета тяжелее воздуха в следующем столетии. В 1871 году Фрэнсис Герберт Уэнам построил первую аэродинамическую трубу , позволившую точно измерять аэродинамические силы. Теорию сопротивления разработал Жан ле Рон д'Аламбер . Густав Кирхгоф , и лорд Рэлей . В 1889 году Шарль Ренар , французский авиационный инженер, стал первым человеком, который обоснованно предсказал мощность, необходимую для продолжительного полета. Отто Лилиенталь , первый человек, добившийся больших успехов в полетах на планерах, был также первым, кто предложил тонкие изогнутые крылья , обеспечивающие высокую подъемную силу и низкое сопротивление. Опираясь на эти разработки, а также на исследования, проведенные в собственной аэродинамической трубе, братья Райт 17 декабря 1903 года подняли в воздух первый самолет с двигателем.

Во времена первых полетов Фредерика Ланчестера , Мартин Кутта и Николай Жуковский независимо друг от друга создали теории, связывающие циркуляцию потока жидкости с подъемной силой. Кутта и Жуковский разработали двумерную теорию крыла. Развивая работы Ланчестера, Людвигу Прандтлю приписывают развитие математики. за теории тонкого профиля и подъемной линии, а также работу с пограничными слоями .

Плакат Минавиапрома по аэродинамике.

По мере увеличения скорости самолета конструкторы начали сталкиваться с проблемами, связанными со сжимаемостью воздуха на скоростях, близких к скорости звука. Различия в потоках воздуха в таких условиях приводят к проблемам в управлении самолетом, увеличению лобового сопротивления из-за ударных волн и угрозе разрушения конструкции из-за аэроупругого флаттера . Отношение скорости потока к скорости звука было названо числом Маха в честь Эрнста Маха, который одним из первых исследовал свойства сверхзвукового потока . Маккуорн Рэнкин и Пьер Анри Гюгонио независимо друг от друга разработали теорию свойств потока до и после ударной волны , а Якоб Акерет возглавил первоначальную работу по расчету подъемной силы и сопротивления сверхзвуковых аэродинамических профилей. Теодор фон Карман и Хью Латимер Драйден ввели термин «трансзвуковой» для описания скоростей потока между критическим числом Маха и 1 Маха, при которых сопротивление быстро увеличивается. Такое быстрое увеличение сопротивления привело к тому, что аэродинамики и авиаторы разошлись во мнениях относительно того, достижим ли сверхзвуковой полет, пока звуковой барьер в 1947 году не был преодолен с помощью самолета Bell X-1 .

К тому времени, когда звуковой барьер был преодолен, понимание аэродинамиками дозвукового и низкого сверхзвукового потока созрело. Холодная война побудила к разработке постоянно развивающейся линейки высокопроизводительных самолетов. Вычислительная гидродинамика началась как попытка определить свойства потока вокруг сложных объектов и быстро выросла до такой степени, что весь самолет можно спроектировать с использованием компьютерного программного обеспечения с испытаниями в аэродинамической трубе, за которыми следуют летные испытания для подтверждения компьютерных прогнозов. Понимание сверхзвуковой и гиперзвуковой аэродинамики созрело с 1960-х годов, и цели аэродинамиков сместились от поведения потока жидкости к разработке транспортного средства, которое предсказуемо взаимодействует с потоком жидкости. Проектирование самолетов для сверхзвуковых и гиперзвуковых условий, а также стремление улучшить аэродинамическую эффективность существующих самолетов и двигательных установок продолжают мотивировать новые исследования в области аэродинамики, в то время как продолжаются работы над важными проблемами базовой аэродинамической теории, связанными с турбулентностью потока. существование и единственность аналитических решений уравнений Навье – Стокса.

Фундаментальные понятия

Полетные силы на самолете с двигателем в горизонтальном полете без ускорения

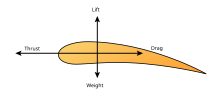
Понимание движения воздуха вокруг объекта (часто называемого полем потока) позволяет рассчитать силы и моменты, действующие на объект. Во многих задачах аэродинамики интересующими силами являются фундаментальные силы полета: подъемная сила , сопротивление , тяга и вес . Из них подъемная сила и сопротивление представляют собой аэродинамические силы, то есть силы, возникающие вследствие потока воздуха над твердым телом. Расчет этих величин часто основывается на предположении, что поле течения ведет себя как континуум. Поля непрерывного потока характеризуются такими свойствами, как скорость потока , давление , плотность и температура , которые могут быть функциями положения и времени. Эти свойства могут быть прямо или косвенно измерены в экспериментах по аэродинамике или рассчитаны, исходя из уравнений сохранения массы, импульса и энергии в воздушных потоках. Плотность, скорость потока и дополнительное свойство вязкость используются для классификации полей потока.

Классификация потоков

Скорость потока используется для классификации потоков по скоростному режиму. Дозвуковые течения – это поля течения, в которых поле скорости воздуха всегда ниже местной скорости звука. Трансзвуковые течения включают как области дозвукового течения, так и области, в которых локальная скорость потока превышает локальную скорость звука. Сверхзвуковые потоки определяются как потоки, в которых скорость потока повсюду превышает скорость звука. Четвертая классификация — гиперзвуковые течения — относится к течениям, скорость которых намного превышает скорость звука. Аэродинамики расходятся во мнениях относительно точного определения гиперзвукового потока.

Сжимаемый поток учитывает различную плотность внутри потока. Дозвуковые течения часто идеализируются как несжимаемые, т. е. плотность предполагается постоянной. Трансзвуковые и сверхзвуковые потоки сжимаемы, и расчеты, не учитывающие изменения плотности в этих полях течения, дадут неточные результаты.

Вязкость связана с силами трения в потоке. В некоторых полях течения вязкие эффекты очень малы, и приближенные решения могут смело пренебрегать вязкими эффектами. Эти приближения называются невязкими течениями. Течения, для которых не пренебрегают вязкостью, называются вязкими течениями. Наконец, аэродинамические проблемы также можно классифицировать по среде потока. Внешняя аэродинамика — это изучение обтекания твердых объектов различной формы (например, вокруг крыла самолета), а внутренняя аэродинамика — изучение течения через каналы внутри твердых объектов (например, через реактивный двигатель).

Предположение о континууме

В отличие от жидкостей и твердых тел, газы состоят из дискретных молекул , которые занимают лишь небольшую часть объема, заполненного газом. На молекулярном уровне поля потока состоят из столкновений множества отдельных молекул газа между собой и с твердыми поверхностями. Однако в большинстве приложений аэродинамики дискретная молекулярная природа газов игнорируется, и предполагается, что поле течения ведет себя как континуум . Это допущение позволяет определять такие свойства жидкости, как плотность и скорость потока, повсюду в потоке.

Обоснованность предположения о континууме зависит от плотности газа и рассматриваемого применения. Чтобы предположение о непрерывности было действительным, средняя длина свободного пробега должна быть намного меньше масштаба длины рассматриваемого приложения. Например, многие приложения аэродинамики имеют дело с самолетами, летающими в атмосферных условиях, где средняя длина свободного пробега составляет порядка микрометров, а тело на порядки больше. В этих случаях масштаб длины летательного аппарата составляет от нескольких метров до нескольких десятков метров, что значительно превышает среднюю длину свободного пробега. Для таких приложений разумно предположение о континууме. Предположение о непрерывности менее справедливо для потоков с чрезвычайно низкой плотностью, например, с теми, с которыми сталкиваются транспортные средства на очень больших высотах (например, 300 000 футов/90 км). или спутники на низкой околоземной орбите . В этих случаях статистическая механика является более точным методом решения проблемы, чем аэродинамика сплошной среды. Число Кнудсена можно использовать для выбора между статистической механикой и непрерывной формулировкой аэродинамики.

Законы сохранения

Предположение о континууме жидкости позволяет решать задачи аэродинамики, используя законы сохранения гидродинамики . Используются три принципа консервации:

Сохранение массы

Сохранение массы требует, чтобы масса не создавалась и не уничтожалась внутри потока; математическая формулировка этого принципа известна как уравнение неразрывности массы .

Сохранение импульса

Математическая формулировка этого принципа может рассматриваться как применение Второго закона Ньютона . Импульс внутри потока изменяется только внешними силами, которые могут включать как поверхностные силы , такие как силы вязкости ( трения ), так и объемные силы , такие как вес . Принцип сохранения импульса может быть выражен либо в виде векторного уравнения, либо разделен на набор из трех скалярных уравнений (компоненты x, y, z).

Сохранение энергии

Уравнение сохранения энергии утверждает, что энергия не создается и не уничтожается внутри потока, и что любое добавление или вычитание энергии в объеме потока вызвано передачей тепла или работой в интересующую область и из нее.

Вместе эти уравнения известны как уравнения Навье – Стокса , хотя некоторые авторы определяют этот термин как включающий только уравнение(я) импульса. Уравнения Навье-Стокса не имеют известного аналитического решения и решаются в современной аэродинамике с использованием вычислительных методов . Поскольку вычислительные методы с использованием высокоскоростных компьютеров исторически не были доступны, а теперь, когда они доступны, высокая вычислительная стоимость решения этих сложных уравнений, упрощения уравнений Навье – Стокса использовались и продолжают использоваться. Уравнения Эйлера представляют собой набор аналогичных уравнений сохранения, в которых пренебрегается вязкость и которые могут использоваться в случаях, когда ожидается, что влияние вязкости будет небольшим. Дальнейшие упрощения приводят к уравнению Лапласа и теории потенциального потока . Кроме того, уравнение Бернулли является одномерным решением уравнений сохранения импульса и энергии.

Закон идеального газа или другое подобное уравнение состояния часто используется в сочетании с этими уравнениями для формирования определенной системы, которая позволяет найти решение для неизвестных переменных.

Разделы аэродинамики

компьютерное моделирование

Аэродинамические проблемы классифицируются по среде течения или свойствам потока, включая скорость потока , сжимаемость и вязкость . Внешняя аэродинамика – это изучение обтекания твердых тел различной формы. Оценка подъемной силы и сопротивления самолета примерами или ударных волн , образующихся перед носом ракеты, являются внешней аэродинамики. Внутренняя аэродинамика — это изучение течения через каналы в твердых объектах. Например, внутренняя аэродинамика включает изучение потока воздуха через реактивный двигатель или через трубу кондиционирования воздуха .

Аэродинамические проблемы также можно классифицировать в зависимости от того, находится ли скорость потока ниже, вблизи или выше скорости звука . Задача называется дозвуковой, если все скорости в задаче меньше скорости звука, трансзвуковой , если присутствуют скорости как ниже, так и выше скорости звука (обычно, когда характерная скорость примерно равна скорости звука), сверхзвуковой , когда Характерная скорость потока больше скорости звука, а гиперзвуковая — когда скорость потока значительно превышает скорость звука. Аэродинамики расходятся во мнениях относительно точного определения гиперзвукового потока; грубое определение считает, что потоки с числами Маха выше 5 являются гиперзвуковыми.

Влияние вязкости на текучесть диктует третью классификацию. Некоторые проблемы могут сталкиваться лишь с очень небольшими эффектами вязкости, и в этом случае вязкость можно считать незначительной. Приближения к этим задачам называются невязкими течениями . Течения, для которых вязкостью нельзя пренебречь, называются вязкими течениями.

Несжимаемая аэродинамика

Дополнительная информация: несжимаемый поток.

Несжимаемый поток – это поток, плотность которого постоянна как во времени, так и в пространстве. Хотя все реальные жидкости сжимаемы, поток часто аппроксимируется как несжимаемый, если эффект изменения плотности вызывает лишь небольшие изменения в расчетных результатах. Это с большей вероятностью будет правдой, когда скорости потока значительно ниже скорости звука. Эффекты сжимаемости более значительны на скоростях, близких к скорости звука или превышающих ее. Число Маха используется для оценки того, можно ли предполагать несжимаемость, в противном случае необходимо учитывать эффекты сжимаемости.

Дозвуковой поток

Дозвуковая (или низкоскоростная) аэродинамика описывает движение жидкости в потоках, скорость которых во всем потоке значительно ниже скорости звука. Существует несколько ветвей дозвукового течения, но возникает особый случай, когда течение невязкое , несжимаемое и безвихревое . Этот случай называется потенциальным потоком и позволяет дифференциальным уравнениям , описывающим поток, представлять собой упрощенную версию уравнений гидродинамики , тем самым предоставляя аэродинамикам ряд быстрых и простых решений.

При решении дозвуковой задачи специалист по аэродинамике должен принять одно решение: учитывать ли эффекты сжимаемости. Сжимаемость – это описание величины изменения плотности потока. Когда влияние сжимаемости на раствор невелико, можно предположить, что плотность постоянна. Тогда проблема заключается в задаче аэродинамики несжимаемой жидкости на малых скоростях. Когда плотность может изменяться, поток называется сжимаемым. В воздухе эффекты сжимаемости обычно игнорируются, когда число Маха в потоке не превышает 0,3 (около 335 футов (102 м) в секунду или 228 миль (366 км) в час при 60 ° F (16 ° C)). При скорости выше 0,3 Маха проблемный поток следует описывать с помощью сжимаемой аэродинамики.

Сжимаемая аэродинамика

Основная статья: Сжимаемый поток

Согласно теории аэродинамики поток считается сжимаемым, если плотность изменяется вдоль линии тока . Это означает, что – в отличие от несжимаемого потока – учитываются изменения плотности. В общем случае это тот случай, когда число Маха части или всего потока превышает 0,3. Значение 0,3 Маха довольно условно, но оно используется потому, что потоки газа с числом Маха ниже этого значения демонстрируют изменения плотности менее 5%. Более того, максимальное изменение плотности на 5% происходит в точке застоя (точке объекта, где скорость потока равна нулю), в то время как изменения плотности вокруг остальной части объекта будут значительно ниже. Трансзвуковые, сверхзвуковые и гиперзвуковые потоки являются сжимаемыми потоками.

Трансзвуковой поток

Основная статья: Трансоник

Термин «трансзвуковой» относится к диапазону скоростей потока чуть ниже и выше местной скорости звука (обычно принимается равной 0,8–1,2 Маха ). Он определяется как диапазон скоростей между критическим числом Маха , когда некоторые части воздушного потока над самолетом становятся сверхзвуковыми , и более высокой скоростью, обычно около 1,2 Маха , когда весь воздушный поток является сверхзвуковым. Между этими скоростями часть воздушного потока является сверхзвуковой, а часть воздушного потока не является сверхзвуковой.

Сверхзвуковой поток

Основная статья: Сверхзвуковой

Сверхзвуковые аэродинамические проблемы связаны со скоростью потока, превышающей скорость звука. Расчет подъемной силы Конкорда во время крейсерского полета может быть примером сверхзвуковой аэродинамической задачи.

Сверхзвуковой поток ведет себя совсем иначе, чем дозвуковой. Жидкости реагируют на разницу в давлении; Изменения давления — это то, как жидкости «приказывают» реагировать на окружающую среду. Следовательно, поскольку звук , по сути, представляет собой бесконечно малую разницу давлений, распространяющуюся через жидкость, скорость звука в этой жидкости можно считать самой высокой скоростью, с которой «информация» может перемещаться в потоке. Наиболее явно это различие проявляется при попадании жидкости на объект. Перед этим объектом жидкость создает застойное давление , поскольку удар о объект приводит движущуюся жидкость в состояние покоя. В жидкости, движущейся с дозвуковой скоростью, это возмущение давления может распространяться вверх по течению, изменяя структуру потока перед объектом и создавая впечатление, что жидкость «знает», что объект находится там, по-видимому, корректируя свое движение и обтекая его. Однако в сверхзвуковом потоке возмущение давления не может распространяться вверх по потоку. Таким образом, когда жидкость наконец достигает объекта, она ударяется о него, и жидкость вынуждена изменить свои свойства – температура , плотность , давление и число Маха — чрезвычайно сильным и необратимым образом, называемым ударной волной . Наличие ударных волн, наряду с эффектами сжимаемости жидкостей с высокой скоростью потока (см. число Рейнольдса ), является центральным различием между сверхзвуковыми и дозвуковыми режимами аэродинамики.

Гиперзвуковой поток

Основная статья: Гиперзвуковой

В аэродинамике гиперзвуковые скорости — это скорости, в высокой степени сверхзвуковые. В 1970-х годах этот термин обычно обозначал скорость 5 Маха (в 5 раз превышающую скорость звука) и выше. Гиперзвуковой режим является разновидностью сверхзвукового режима. Гиперзвуковое течение характеризуется высокотемпературным течением за ударной волной, вязким взаимодействием и химической диссоциацией газа.

Сопутствующая терминология

Различные типы анализа обтекания профиля:

   потенциального потока Теория

   течения в пограничном слое Теория

   турбулентного следа Анализ

Режимы несжимаемого и сжимаемого течения вызывают множество сопутствующих явлений, таких как пограничные слои и турбулентность.

Пограничные слои

Основная статья: Пограничный слой

Понятие пограничного слоя важно во многих задачах аэродинамики. Вязкость и жидкостное трение в воздухе считаются существенными только в этом тонком слое. Это предположение делает описание такой аэродинамики гораздо более поддающимся математическому анализу.

Турбулентность

Основная статья: Турбулентность

В аэродинамике турбулентность характеризуется хаотичным изменением свойств потока. К ним относятся диффузия с низким импульсом, конвекция с высоким импульсом и быстрое изменение давления и скорости потока в пространстве и времени. Поток, не являющийся турбулентным, называется ламинарным .

Аэродинамика в других областях

Инженерное проектирование

Дополнительная информация: Автомобильная аэродинамика.

Аэродинамика является важным элементом конструкции транспортных средств , в том числе дорожных и грузовых автомобилей , где основной целью является снижение коэффициента лобового сопротивления транспортного средства , и гоночных автомобилей , где помимо снижения лобового сопротивления целью является также увеличение общего уровня прижимной силы . Аэродинамика также важна для прогнозирования сил и моментов, действующих на парусные суда . Он используется при проектировании механических компонентов, таких как головки жестких дисков . Инженеры-строители прибегают к аэродинамике, и особенно к аэроупругости , при расчете ветровых нагрузок при проектировании больших зданий, мостов и ветряных турбин .

Аэродинамика внутренних каналов важна в системах отопления/вентиляции , газопроводах и в автомобильных двигателях , где детальная структура потока сильно влияет на производительность двигателя.

Экологический дизайн

Городскую аэродинамику изучают градостроители и дизайнеры, стремящиеся улучшить удобства открытых пространств или создать городской микроклимат для уменьшения воздействия городского загрязнения. Область экологической аэродинамики описывает способы, которыми атмосферная циркуляция и механика полета влияют на экосистемы.

Аэродинамические уравнения используются в численном прогнозе погоды .

Контроль мяча в спорте

Виды спорта, в которых аэродинамика имеет решающее значение, включают футбол , настольный теннис , крикет , бейсбол и гольф , в которых большинство игроков могут контролировать траекторию мяча, используя « эффект Магнуса ».

См. также

• Воздухоплавание
• Аэростатика
• Авиация
• Полет насекомых – как летают жуки
• Список тем аэрокосмической техники
• Список инженерных тем
• Конструкция носового конуса
• Гидродинамика
• Вычислительная гидродинамика

Дальнейшее чтение

Общая аэродинамика

• Андерсон, Джон Д. (2007). Основы аэродинамики (4-е изд.). МакГроу-Хилл. ISBN  978-0-07-125408-3 . OCLC   60589123 .
• Бертен, Джей-Джей; Смит, М.Л. (2001). Аэродинамика для инженеров (4-е изд.). Прентис Холл. ISBN  0-13-064633-4 . OCLC   47297603 .
• Смит, Хьюберт К. (1991). Иллюстрированное руководство по аэродинамике (2-е изд.). МакГроу-Хилл. ISBN  0-8306-3901-2 . ОСЛК   24319048 .
• Крейг, Гейл (2003). Введение в аэродинамику . Регенеративный пресс. ISBN  0-9646806-3-7 . OCLC   53083897 .

Дозвуковая аэродинамика

• Кац, Джозеф; Плоткин, Аллен (2001). Аэродинамика малых скоростей (2-е изд.). Издательство Кембриджского университета. ISBN  0-521-66552-3 . OCLC   43970751 .
• Оберт, Эд (2009). Аэродинамический дизайн транспортных самолетов в Google Книгах . Делфт; О практической аэродинамике в промышленности и ее влиянии на конструкцию самолетов. ISBN   978-1-58603-970-7 .

Трансзвуковая аэродинамика

• Молден, Тревор Х. (1990). Основы трансзвукового потока . Издательство Кригер. ISBN  0-89464-441-6 . ОСЛК   20594163 .
• Коул, Джулиан Д; Кук, Л. Памела (1986). Трансзвуковая аэродинамика . Северная Голландия. ISBN  0-444-87958-7 . ОСЛК   13094084 .

Сверхзвуковая аэродинамика

• Ферри, Антонио (2005). Элементы аэродинамики сверхзвуковых потоков (изд. Феникса). Дуврские публикации. ISBN  0-486-44280-2 . OCLC   58043501 .
• Шапиро, Ашер Х. (1953). Динамика и термодинамика течения сжимаемой жидкости, Том 1 . Рональд Пресс. ISBN  978-0-471-06691-0 . OCLC   11404735 .
• Андерсон, Джон Д. (2004). Современный сжимаемый поток . МакГроу-Хилл. ISBN  0-07-124136-1 . OCLC   71626491 .
• Липманн, HW ; Рошко, А. (2002). Элементы газодинамики . Дуврские публикации. ISBN  0-486-41963-0 . OCLC   47838319 .
• фон Мизес, Ричард (2004). Математическая теория течения сжимаемой жидкости . Дуврские публикации. ISBN  0-486-43941-0 . OCLC   56033096 .
• Ходж, Британская Колумбия; Кениг К. (1995). Динамика сжимаемой жидкости с приложениями для персонального компьютера . Прентис Холл. ISBN  0-13-308552-Х . OCLC   31662199 .

Гиперзвуковая аэродинамика

• Андерсон, Джон Д. (2006). Гиперзвуковая и высокотемпературная газодинамика (2-е изд.). АААА. ISBN  1-56347-780-7 . OCLC   68262944 .
• Хейс, Уоллес Д .; Пробштейн, Рональд Ф. (2004). Гиперзвуковое невязкое течение . Дуврские публикации. ISBN  0-486-43281-5 . OCLC   53021584 .

История аэродинамики

• Шанют, Октава (1997). Прогресс в летательных аппаратах . Дуврские публикации. ISBN  0-486-29981-3 . OCLC   37782926 .
• фон Карман, Теодор (2004). Аэродинамика: избранные темы в свете их исторического развития . Дуврские публикации. ISBN  0-486-43485-0 . OCLC   53900531 .
• Андерсон, Джон Д. (1997). История аэродинамики: и ее влияние на летательные аппараты . Издательство Кембриджского университета. ISBN  0-521-45435-2 . OCLC   228667184 .

Аэродинамика, связанная с техникой

Наземная техника

• Кац, Джозеф (1995). Аэродинамика гоночного автомобиля: проектирование для скорости . Издательство Бентли. ISBN  0-8376-0142-8 . OCLC   181644146 .
• Барнард, Р.Х. (2001). Аэродинамический дизайн дорожных транспортных средств (2-е изд.). Издательство Мехаэро. ISBN  0-9540734-0-1 . OCLC   47868546 .

Самолеты

• Эшли, Холт; Ландал, Мартен (1985). Аэродинамика крыльев и тел (2-е изд.). Дуврские публикации. ISBN  0-486-64899-0 . OCLC   12021729 .
• Эбботт, Ира Х.; фон Дёнхофф, AE (1959). Теория секций крыла: включая сводные данные о профиле крыла . Дуврские публикации. ISBN  0-486-60586-8 . OCLC   171142119 .
• Клэнси, ЖЖ (1975). Аэродинамика . Питман Паблишинг Лимитед. ISBN  0-273-01120-0 . OCLC   16420565 .

Вертолеты

• Лейшман, Дж. Гордон (2006). Принципы аэродинамики вертолетов (2-е изд.). Издательство Кембриджского университета. ISBN  0-521-85860-7 . OCLC   224565656 .
• Праути, Раймонд В. (2001). Характеристики, устойчивость и управляемость вертолета . Издательство Кригера. ISBN  1-57524-209-5 . OCLC   212379050 .
• Седдон, Дж.; Ньюман, Саймон (2001). Базовая аэродинамика вертолета: описание основных принципов механики жидкости и динамики полета одновинтового вертолета . АААА. ISBN  1-56347-510-3 . OCLC   47623950 .

Ракеты

• Нильсон, Джек Н. (1988). Аэродинамика ракет . АААА. ISBN  0-9620629-0-1 . OCLC   17981448 .

Модель самолета

• Саймонс, Мартин (1999). Аэродинамика моделей самолетов (4-е изд.). Трансатлантические публикации, Inc. ISBN  1-85486-190-5 . OCLC   43634314 .

Связанные отрасли аэродинамики

Аэротермодинамика

• Хиршель, Эрнст Х. (2004). Основы аэротермодинамики . Спрингер. ISBN  3-540-22132-8 . OCLC   228383296 .
• Бертин, Джон Дж. (1993). Гиперзвуковая аэротермодинамика . АААА. ISBN  1-56347-036-5 . ОСЛК   28422796 .

Аэроупругость

• Бисплингхофф, Раймонд Л.; Эшли, Холт; Халфман, Роберт Л. (1996). Аэроупругость . Дуврские публикации. ISBN  0-486-69189-6 . OCLC   34284560 .
• Фунг, Ю.К. (2002). Введение в теорию аэроупругости (изд. Феникса). Дуврские публикации. ISBN  0-486-49505-1 . OCLC   55087733 .

Пограничные слои

• Янг, AD (1989). Пограничные слои . АААА. ISBN  0-930403-57-6 . OCLC   19981526 .
• Розенхед, Л. (1988). Ламинарные пограничные слои . Дуврские публикации. ISBN  0-486-65646-2 . ОСЛК   17619090 .

Турбулентность

• Теннекес, Х. ; Ламли, Дж. Л. (1972). Первый курс турбулентности . Массачусетский технологический институт Пресс. ISBN  0-262-20019-8 . ОСЛК   281992 .
• Папа, Стивен Б. (2000). Турбулентные потоки . Издательство Кембриджского университета. ISBN  0-521-59886-9 . OCLC   174790280 .

Внешние ссылки

• Руководство НАСА по аэродинамике . Архивировано 15 июля 2012 г. в Wayback Machine .
• Аэродинамика для студентов
• Аэродинамика для пилотов (в архиве)
• Аэродинамика и тюнинг гоночных автомобилей (в архиве)
• Проекты, связанные с аэродинамикой . Архивировано 13 декабря 2018 г. в Wayback Machine .
• eFluids Аэродинамика велосипеда . Архивировано 15 декабря 2009 г. в Wayback Machine .
• Применение аэродинамики в Формуле-1 (F1) (в архиве)
• Аэродинамика в автогонках . Архивировано 6 декабря 2009 г. в Wayback Machine .
• Аэродинамика птиц . Архивировано 24 марта 2010 г. в Wayback Machine .
• Индекс аэродинамики НАСА