число Маха

Число Маха ( М или Ма ), часто только Маха , ( / m ɑː k / ; Немецкий: [max] ) — безразмерная величина в гидродинамике, представляющая собой отношение скорости потока за границей к местной скорости звука . ^[1]^[2]Назван в честь чешского физика и философа Эрнста Маха .

\mathrm {M} ={\frac {u}{c}},

где:

M – местное число Маха,

u

- локальная скорость потока относительно границ (внутренних, например, объекта, погруженного в поток, или внешнего, например, канала), и

c

— скорость звука в среде, которая в воздухе изменяется пропорционально квадратному корню из термодинамической температуры .

По определению, при скорости 1 Маха локальная скорость потока $u$ равна скорости звука. При скорости 0,65 $Маха u$ составляет 65% скорости звука (дозвуковая), а при скорости 1,35 $Маха u$ на 35% быстрее скорости звука (сверхзвуковой). Пилоты высотных аэрокосмических транспортного средства аппаратов используют число Маха полета, чтобы выразить истинную воздушную скорость , но поле потока вокруг транспортного средства варьируется в трех измерениях с соответствующими вариациями местного числа Маха.

Локальная скорость звука и, следовательно, число Маха зависят от температуры окружающего газа. Число Маха в основном используется для определения приближения, с помощью которого поток можно рассматривать как несжимаемый поток . Среда может быть газом или жидкостью. Граница может перемещаться в среде или быть неподвижной, пока среда течет вдоль нее, или они могут двигаться обе с разными скоростями : значение имеет их относительная скорость по отношению друг к другу. Граница может быть границей объекта, погруженного в среду, или канала, такого как сопло , диффузор или аэродинамическая труба, направляющая среду. Поскольку число Маха определяется как отношение двух скоростей, оно является безразмерной величиной. Если M <0,2–0,3 и поток квазистационарный и изотермический , эффекты сжимаемости будут небольшими, и можно использовать упрощенные уравнения потока несжимаемой жидкости. ^[1]^[2]

Этимология

Число Маха названо в честь физика и философа Эрнста Маха. ^[3] по предложению авиационного инженера Якоба Акерета в 1929 году. ^[4] Слово Мах всегда пишется с заглавной буквы, поскольку оно происходит от имени собственного, а поскольку число Маха является безразмерной величиной, а не единицей измерения , это число следует после слова Мах; второе число Маха - Маха 2 вместо 2 Маха (или Маха). Это чем-то напоминает раннюю современную единицу измерения глубины океана (синоним сажени ), которая также указывалась на единицу измерения и, возможно, повлияла на использование термина Мах. В течение десятилетия, предшествовавшего полету человека со скоростью, превышающей скорость звука , авиационные инженеры называли скорость звука числом Маха , а не 1 Маха . ^[5]

Обзор

Число Маха является мерой характеристик сжимаемости потока жидкости : жидкость (воздух) ведет себя под влиянием сжимаемости аналогичным образом при заданном числе Маха, независимо от других переменных. ^[6] Согласно модели Международной стандартной атмосферы , сухой воздух на среднем уровне моря , стандартная температура 15 °C (59 °F), скорость звука составляет 340,3 метра в секунду (1116,5 футов/с; 761,23 миль в час; 1225,1 км/ч; 661,49 кун). ^[7] Скорость звука не является константой; в газе она увеличивается пропорционально квадратному корню из абсолютной температуры , а поскольку температура атмосферы обычно снижается с увеличением высоты от уровня моря до 11 000 метров (36 089 футов), скорость звука также уменьшается. Например, в стандартной модели атмосферы температура снижается до -56,5 ° C (-69,7 ° F) на высоте 11 000 метров (36 089 футов) с соответствующей скоростью звука ( 1 Маха) 295,0 метров в секунду (967,8 футов / с); 659,9 миль в час; 1062 км/ч; 573,4 узла), 86,7% от значения уровня моря.

Появление в уравнении неразрывности

В качестве меры сжимаемости потока число Маха может быть получено из соответствующего масштабирования уравнения неразрывности . ^[8] Полное уравнение неразрывности для общего потока жидкости: ${\partial \rho \over {\partial t}}+\nabla \cdot (\rho {\bf {u}})=0\equiv -{1 \over {\rho }}{D\rho \over {Dt}}=\nabla \cdot {\bf {u}}$ где $D/Dt$ является материальной производной , $\rho$ плотность а , ${\bf {u}}$ это скорость потока . Для изэнтропическим давлением, изменений плотности, вызванных $dp=c^{2}d\rho$ где $c$ это скорость звука. Тогда уравнение неразрывности можно немного изменить, чтобы учесть это соотношение: $-{1 \over {\rho c^{2}}}{Dp \over {Dt}}=\nabla \cdot {\bf {u}}$ Следующим шагом является обезразмеривание переменных как таковых: ${\bf {x}}^{*}={\bf {x}}/L,\quad t^{*}=Ut/L,\quad {\bf {u}}^{*}={\bf {u}}/U,\quad p^{*}=(p-p_{\infty })/\rho _{0}U^{2},\quad \rho ^{*}=\rho /\rho _{0}$ где $L$ – характерный масштаб длины, $U$ – характерный масштаб скорости, $p_{\infty }$ - эталонное давление, и $\rho _{0}$ – эталонная плотность. Тогда безразмерная форма уравнения неразрывности может быть записана как: $-{U^{2} \over {c^{2}}}{1 \over {\rho ^{*}}}{Dp^{*} \over {Dt^{*}}}=\nabla ^{*}\cdot {\bf {u}}^{*}\implies -{\text{M}}^{2}{1 \over {\rho ^{*}}}{Dp^{*} \over {Dt^{*}}}=\nabla ^{*}\cdot {\bf {u}}^{*}$ где число Маха ${\text{M}}=U/c$ . В том пределе, что ${\text{M}}\rightarrow 0$ , уравнение неразрывности сводится к $\nabla \cdot {\bf {u}}=0$ — это стандартное требование для несжимаемого потока .

Классификация режимов Маха

Хотя термины «дозвуковой» и «сверхзвуковой» в чистом смысле относятся к скоростям ниже и выше местной скорости звука соответственно, аэродинамики часто используют одни и те же термины, чтобы говорить об определенных диапазонах значений Маха. Это происходит из-за наличия трансзвукового режима вокруг полета (набегающего потока) M = 1, где аппроксимации уравнений Навье-Стокса, используемые для дозвукового проектирования, больше не применимы; Самое простое объяснение состоит в том, что обтекание планера локально начинает превышать M = 1, хотя число Маха набегающего потока ниже этого значения.

Между тем, сверхзвуковой режим обычно используется, чтобы говорить о наборе чисел Маха, для которых можно использовать линеаризованную теорию, где, например, поток ( воздуха ) не вступает в химическую реакцию и где теплообменом между воздухом и транспортным средством можно разумно пренебречь. в расчетах.

В следующей таблице режимы или диапазоны значений Маха указаны , а не чистые значения слов «дозвуковой» и «сверхзвуковой» .

Как правило, НАСА определяет высокий гиперзвук как любое число Маха от 10 до 25, а скорость входа в атмосферу - как любое число, превышающее 25 Маха. К самолетам, работающим в этом режиме, относятся космические шаттлы и различные космические самолеты, находящиеся в стадии разработки.

Режим	Скорость полета					Общие характеристики самолета
Режим	(Мах)	(узлы)	(миль в час)	(км/ч)	(РС)	Общие характеристики самолета
Дозвуковой	<0,8	<530	<609	<980	<273	Чаще всего это винтовые и коммерческие турбовентиляторные самолеты с тонкими крыльями с большим удлинением и закругленными деталями, такими как носовая и передняя кромки. Диапазон дозвуковых скоростей - это диапазон скоростей, в котором весь поток воздуха над самолетом составляет менее 1 Маха. Критическое число Маха (Mcrit) - это наименьшее число Маха набегающего потока, при котором поток воздуха над любой частью самолета впервые достигает Маха. 1. Итак, в диапазон дозвуковых скоростей входят все скорости, меньшие Мкрит.
околозвуковой	0.8–1.2	530–794	609–914	980–1,470	273–409	Трансзвуковые самолеты почти всегда имеют стреловидные крылья , вызывающие задержку расхождения сопротивления, и часто имеют конструкцию, соответствующую принципам правила зоны Уиткомба . Трансзвуковой диапазон скоростей — это диапазон скоростей, в котором обтекание различных частей летательного аппарата воздушным потоком находится между дозвуковыми и сверхзвуковыми. Поэтому режим полета от Мкрита до 1,3 Маха называется трансзвуковым диапазоном.
сверхзвуковой	1.2–5.0	794–3,308	915–3,806	1,470–6,126	410–1,702	Диапазон сверхзвуковых скоростей — это диапазон скоростей, в котором весь поток воздуха над самолетом является сверхзвуковым (более 1 Маха). Но воздушный поток, встречающийся с передними кромками, изначально замедляется, поэтому скорость набегающего потока должна быть немного больше 1 Маха, чтобы весь поток над самолетом был сверхзвуковым. Принято считать, что диапазон сверхзвуковых скоростей начинается со скорости набегающего потока, превышающей 1,3 Маха. Самолеты, предназначенные для полетов со сверхзвуковыми скоростями, демонстрируют большие различия в своей аэродинамической конструкции из-за радикальных различий в поведении потоков со скоростью выше 1 Маха. Острые кромки, тонкие аэродинамические секции и цельноповоротное хвостовое оперение / переднее оперение являются обычным явлением. Современные боевые самолеты должны идти на компромисс, чтобы поддерживать управляемость на малых скоростях; «Настоящие» сверхзвуковые проекты включают F-104 Starfighter , МиГ-31 , North American XB-70 Valkyrie , SR-71 Blackbird и BAC/Aérospatiale Concorde .
Гиперзвуковой	5.0–10.0	3,308–6,615	3,806–7,680	6,126–12,251	1,702–3,403	Х -15 со скоростью 6,72 Маха является одним из самых быстрых пилотируемых самолетов. Также охлаждаемая никель - титановая кожа; высокоинтегрированные (из-за доминирования интерференционных эффектов: нелинейное поведение означает, что суперпозиция результатов для отдельных компонентов недействительна), маленькие крылья, такие как у X-51A Waverider со скоростью 5 Маха .
Высоко-гиперзвуковой	10.0–25.0	6,615–16,537	7,680–19,031	12,251–30,626	3,403–8,508	NASA X-43 со скоростью 9,6 Маха является одним из самых быстрых самолетов. Температурный контроль становится доминирующим фактором при проектировании. Конструкция должна быть либо рассчитана на работу в горячем состоянии, либо защищена специальной силикатной плиткой или чем-то подобным. Химически реагирующий поток также может вызвать коррозию обшивки автомобиля, поскольку свободный атомарный кислород присутствует в очень высокоскоростных потоках. Гиперзвуковые конструкции часто вынуждены принимать тупые конфигурации из-за аэродинамического нагрева, возрастающего при уменьшении радиуса кривизны .
повторного входа Скорость	>25,0	>16 537	>19 031	>30 626	>8508	Абляционный теплозащитный экран ; маленькие крылья или их отсутствие; тупая форма. российский «Авангард» (гиперзвуковой планирующий аппарат) Утверждается, что способен развивать скорость до 27 Маха.

Высокоскоростное обтекание объектов

Полет можно условно разделить на шесть категорий:

Режим	Дозвуковой	околозвуковой	Скорость звука	сверхзвуковой	Гиперзвуковой	Гиперскорость
Мах	<0,8	0.8–1.2	1.0	1.2–5.0	5.0–10.0	>8,8

Для сравнения: необходимая скорость для низкой околоземной орбиты составляет примерно 7,5 км/с = 25,4 Маха в воздухе на больших высотах.

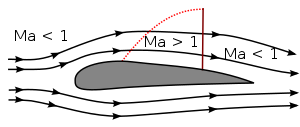
На околозвуковых скоростях поле течения вокруг объекта включает как дозвуковую, так и сверхзвуковую части. Трансзвуковой период начинается с появлением вокруг объекта первых зон течения М > 1. В случае аэродинамического профиля (например, крыла самолета) это обычно происходит над крылом. Сверхзвуковой поток может замедлиться до дозвукового только при нормальном толчке; обычно это происходит перед задней кромкой. (Рис.1а)

С увеличением скорости зона течения М > 1 увеличивается как в сторону передней, так и в сторону задней кромки. При достижении и прохождении М = 1 нормальный скачок достигает задней кромки и становится слабым косым скачком: течение над скачком замедляется, но остается сверхзвуковым. Впереди объекта создается нормальный скачок уплотнения, и единственной дозвуковой зоной в поле потока является небольшая область вокруг передней кромки объекта. (Рис.1б)


(а)	(б)

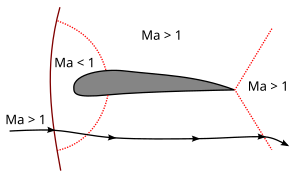
Рис. 1. Число Маха при околозвуковом обтекании профиля; М < 1 (а) и М > 1 (б).

Когда самолет превышает 1 Маха (т.е. звуковой барьер ), прямо перед самолетом создается большая разница давления . Эта резкая разница давлений, называемая ударной волной , распространяется назад и наружу от самолета в форме конуса (так называемый конус Маха ). Именно эта ударная волна вызывает звуковой удар , слышимый, когда над головой пролетает быстро движущийся самолет. Человек внутри самолета этого не услышит. Чем выше скорость, тем уже конус; при чуть большем M = 1 это вообще не конус, а ближе к слегка вогнутой плоскости.

На полностью сверхзвуковой скорости ударная волна начинает принимать форму конуса и течение либо полностью сверхзвуковое, либо (в случае тупого объекта) между носовой частью объекта и создаваемой им впереди ударной волной остается лишь очень маленькая дозвуковая область потока. самого себя. (В случае острого предмета между носом и ударной волной воздуха нет: ударная волна начинается от носа.)

По мере увеличения числа Маха увеличивается и сила ударной волны , и конус Маха становится все более узким. Когда поток жидкости пересекает ударную волну, его скорость уменьшается, а температура, давление и плотность увеличиваются. Чем сильнее шок, тем значительнее изменения. При достаточно больших числах Маха температура над ударной волной возрастает настолько, что начинаются ионизация и диссоциация молекул газа за ударной волной. Такие течения называются гиперзвуковыми.

Понятно, что любой объект, движущийся с гиперзвуковой скоростью, будет также подвергаться воздействию тех же экстремальных температур, что и газ за носовой ударной волной, и, следовательно, выбор термостойких материалов становится важным.

Высокоскоростное течение в канале

Когда поток в канале становится сверхзвуковым, происходит одно существенное изменение. Сохранение массового расхода заставляет ожидать, что сжатие канала потока приведет к увеличению скорости потока (т.е. сужение канала приводит к более быстрому потоку воздуха), и на дозвуковых скоростях это справедливо. Однако как только поток становится сверхзвуковым, соотношение площади потока и скорости меняется на противоположное: расширение канала фактически увеличивает скорость.

Очевидный результат: для ускорения потока до сверхзвука необходимо сужающееся-расширяющееся сопло, в котором сужающаяся часть ускоряет поток до звуковых скоростей, а расширяющаяся часть продолжает ускорение. Такие сопла называются соплами де Лаваля , и в крайних случаях они способны развивать гиперзвуковую скорость (13 Маха (15 900 км/ч; 9 900 миль в час) при 20 ° C).

Авиационный махометр или электронная система полетной информации ( EFIS ) может отображать число Маха, полученное на основе давления торможения ( трубка Пито ) и статического давления.

Расчет

Если известна скорость звука, число Маха, с которым летит самолет, можно рассчитать по формуле

\mathrm {M} ={\frac {u}{c}}

где:

М — число Маха

u - скорость движущегося самолета,

c — скорость звука на данной высоте (точнее, температура)

а скорость звука зависит от термодинамической температуры как:

c={\sqrt {\gamma \cdot R_{*}\cdot T}},

где:

\gamma \,

- отношение удельной теплоты газа при постоянном давлении к теплоте при постоянном объеме (1,4 для воздуха)

R_{*}

– удельная газовая постоянная воздуха.

T,

– статическая температура воздуха.

Если скорость звука неизвестна, число Маха можно определить путем измерения различных давлений воздуха (статического и динамического) и использования следующей формулы, полученной из уравнения Бернулли для чисел Маха менее 1,0. Предполагая, что воздух является идеальным газом , формула для расчета числа Маха в дозвуковом сжимаемом потоке выглядит следующим образом: ^[9]

\mathrm {M} ={\sqrt {{\frac {2}{\gamma -1}}\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {\gamma -1}{\gamma }}-1\right]}}\,

где:

q _c – ударное давление (динамическое давление),

p — статическое давление

\gamma \,

- отношение удельной теплоты газа при постоянном давлении к теплоте при постоянном объеме (1,4 для воздуха)

Формула для расчета числа Маха в сверхзвуковом сжимаемом потоке получена из сверхзвукового уравнения Пито Рэлея :

{\frac {p_{t}}{p}}=\left[{\frac {\gamma +1}{2}}\mathrm {M} ^{2}\right]^{\frac {\gamma }{\gamma -1}}\cdot \left[{\frac {\gamma +1}{1-\gamma +2\gamma \,\mathrm {M} ^{2}}}\right]^{\frac {1}{\gamma -1}}

Расчет числа Маха по давлению в трубке Пито

Число Маха является функцией температуры и истинной воздушной скорости. самолета летные приборы Однако работают, используя перепад давления для расчета числа Маха, а не температуру.

Предполагая, что воздух является идеальным газом , формула для расчета числа Маха в дозвуковом сжимаемом потоке находится из уравнения Бернулли для M <1 (выше): ^[9]

\mathrm {M} ={\sqrt {5\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {2}{7}}-1\right]}}\,

Формулу для расчета числа Маха в сверхзвуковом сжимаемом потоке можно найти из сверхзвукового уравнения Пито Рэлея (см. выше) с использованием параметров для воздуха:

\mathrm {M} \approx 0.88128485{\sqrt {\left({\frac {q_{c}}{p}}+1\right)\left(1-{\frac {1}{7\,\mathrm {M} ^{2}}}\right)^{2.5}}}

где:

q _c — динамическое давление, измеренное за нормальным скачком.

Как можно видеть, M появляется в обеих частях уравнения, и для практических целей для численного решения необходимо использовать алгоритм поиска корня (уравнение представляет собой септическое уравнение в M ² и хотя некоторые из них можно решить явно, теорема Абеля–Руффини гарантирует, что не существует общей формы корней этих многочленов). Сначала определяется, действительно ли M превышает 1,0, путем расчета M из дозвукового уравнения. Если в этой точке M больше 1,0, то значение M из дозвукового уравнения используется в качестве начального условия для итерации сверхзвукового уравнения с фиксированной точкой, которое обычно сходится очень быстро. ^[9] Альтернативно метод Ньютона можно использовать .

См. также

Критическое число Маха - концепция аэродинамики
Махметр – Летательный прибор
Ramjet - сверхзвуковой атмосферный реактивный двигатель.
ГПВРД - реактивный двигатель, в котором сгорание происходит в сверхзвуковом потоке воздуха.
Скорость звука - Скорость звуковой волны в упругой среде.
Истинная воздушная скорость - скорость самолета относительно воздушной массы, через которую он летит.
Порядки величины (скорости) - Сравнение широкого диапазона скоростей.

Примечания

^ Перейти обратно: ^а ^б Янг, Дональд Ф.; Мансон, Брюс Р.; Окииси, Теодор Х .; Хюбш, Уэйд В. (21 декабря 2010 г.). Краткое введение в механику жидкости (5-е изд.). Джон Уайли и сыновья. п. 95. ИСБН 978-0-470-59679-1 . LCCN 2010038482 . OCLC 667210577 . ОЛ 24479108М .
^ Перейти обратно: ^а ^б Гребель, Уильям П. (19 января 2001 г.). Инженерная механика жидкости (1-е изд.). ЦРК Пресс . п. 16. ISBN 978-1-56032-733-2 . OCLC 1034989004 . ОЛ 9794889М .
^ «Эрнст Мах» . Британская энциклопедия . 2016 . Проверено 6 января 2016 г.
^ Якоб Акерет: Сопротивление воздуха на очень высоких скоростях. Schweizerische Bauzeitung 94 (октябрь 1929 г.), стр. 179–183. См. также: Н. Ротт: Якоб Аккерт и история числа Маха. Ежегодный обзор механики жидкости 17 (1985), стр. 1–9.
^ Боди, Уоррен М., Lockheed P-38 Lightning , Widewing Publications ISBN 0-9629359-0-5 .
^ Нэнси Холл (ред.). «Число Маха» . НАСА .
^ Клэнси, LJ (1975), Аэродинамика, Таблица 1, Pitman Publishing, Лондон, ISBN 0-273-01120-0
^ Кунду, ПиДжей; Коэн, ИМ; Даулинг, Д.Р. (2012). Механика жидкости (5-е изд.). Академическая пресса. стр. 148–149. ISBN 978-0-12-382100-3 .
^ Перейти обратно: ^а ^б ^с Олсон, Уэйн М. (2002). «AFFTC-TIH-99-02, Летные испытания летательных аппаратов ». ( ПДФ ). Летно-испытательный центр ВВС, авиабаза Эдвардс, Калифорния, ВВС США. Архивировано 4 сентября 2011 года в Wayback Machine.

Внешние ссылки

Gas Dynamics Toolbox Рассчитать число Маха и параметры нормальной ударной волны для смесей идеальных и несовершенных газов.
Страница НАСА, посвященная числу Маха . Интерактивный калькулятор числа Маха.
Калькулятор стандартной атмосферы NewByte и преобразователь скорости

[Young_et_al-1] Перейти обратно: ^а ^б Янг, Дональд Ф.; Мансон, Брюс Р.; Окииси, Теодор Х .; Хюбш, Уэйд В. (21 декабря 2010 г.). Краткое введение в механику жидкости (5-е изд.). Джон Уайли и сыновья. п. 95. ИСБН 978-0-470-59679-1 . LCCN 2010038482 . OCLC 667210577 . ОЛ 24479108М .

[Graebel-2] Перейти обратно: ^а ^б Гребель, Уильям П. (19 января 2001 г.). Инженерная механика жидкости (1-е изд.). ЦРК Пресс . п. 16. ISBN 978-1-56032-733-2 . OCLC 1034989004 . ОЛ 9794889М .

[3] «Эрнст Мах» . Британская энциклопедия . 2016 . Проверено 6 января 2016 г.

[4] Якоб Акерет: Сопротивление воздуха на очень высоких скоростях. Schweizerische Bauzeitung 94 (октябрь 1929 г.), стр. 179–183. См. также: Н. Ротт: Якоб Аккерт и история числа Маха. Ежегодный обзор механики жидкости 17 (1985), стр. 1–9.

[5] Боди, Уоррен М., Lockheed P-38 Lightning , Widewing Publications ISBN 0-9629359-0-5 .

[NASA-6] Нэнси Холл (ред.). «Число Маха» . НАСА .

[7] Клэнси, LJ (1975), Аэродинамика, Таблица 1, Pitman Publishing, Лондон, ISBN 0-273-01120-0

[8] Кунду, ПиДжей; Коэн, ИМ; Даулинг, Д.Р. (2012). Механика жидкости (5-е изд.). Академическая пресса. стр. 148–149. ISBN 978-0-12-382100-3 .

[Olson-9] Перейти обратно: ^а ^б ^с Олсон, Уэйн М. (2002). «AFFTC-TIH-99-02, Летные испытания летательных аппаратов ». ( ПДФ ). Летно-испытательный центр ВВС, авиабаза Эдвардс, Калифорния, ВВС США. Архивировано 4 сентября 2011 года в Wayback Machine.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]