Число Нуссельта

В термогидродинамике ( число Нуссельта Nu , по имени Вильгельма Нуссельта отношение общей теплопередачи к кондуктивной теплопередаче на границе жидкости ) — . Полный теплообмен сочетает в себе проводимость и конвекцию . Конвекция включает в себя как адвекцию (движение жидкости), так и диффузию (проводимость). Проводящая составляющая измеряется в тех же условиях, что и конвективная, но для гипотетически неподвижной жидкости. Это безразмерное число жидкости , тесно связанное с числом Рэлея .

Число Нуссельта первого порядка представляет собой передачу тепла за счет чистой проводимости. Значение от 1 до 10 характерно для снарядного или ламинарного течения . Большее число Нуссельта соответствует более активной конвекции, с турбулентным потоком обычно в диапазоне 100–1000.

Аналогичным безразмерным свойством является число Био , которое касается теплопроводности твердого тела, а не жидкости. Массопереносным . числа Нуссельта является число Шервуда аналогом

Определение

Число Нуссельта представляет собой отношение общей теплопередачи (конвекция + проводимость) к кондуктивной теплопередаче через границу. Тепловые потоки конвекции и проводимости параллельны друг другу и нормали к граничной поверхности, а все перпендикулярны среднему потоку в простом случае жидкости.

$\mathrm {Nu} _{L}={\frac {\mbox{Total heat transfer }}{\mbox{Conductive heat transfer }}}={\frac {h}{k/L}}={\frac {hL}{k}}$

где h – коэффициент конвективной теплоотдачи потока, L – характерная длина , k – теплопроводность жидкости.

• Выбор характерной длины следует производить в направлении роста (или толщины) пограничного слоя; Некоторыми примерами характерной длины являются: внешний диаметр цилиндра в (внешнем) поперечном потоке (перпендикулярно оси цилиндра), длина вертикальной пластины, подвергающейся естественной конвекции , или диаметр сферы. Для сложных форм длину можно определить как объем жидкого тела, разделенный на площадь поверхности.
• Теплопроводность жидкости обычно (но не всегда) оценивается по температуре пленки , которая для инженерных целей может быть рассчитана как среднее значение температуры объемной жидкости и температуры поверхности стенки.

В отличие от определения, данного выше, известного как среднее число Нуссельта , локальное число Нуссельта определяется путем принятия длины за расстояние от границы поверхности. до местной достопримечательности.

$\mathrm {Nu} _{x}={\frac {h_{x}x}{k}}$

Среднее : или среднее число получается путем интегрирования выражения по интересующему диапазону, например

${\overline {\mathrm {Nu} }}={\frac {{\frac {1}{L}}\int _{0}^{L}h_{x}\ dx\ L}{k}}={\frac {{\overline {h}}L}{k}}$

Контекст

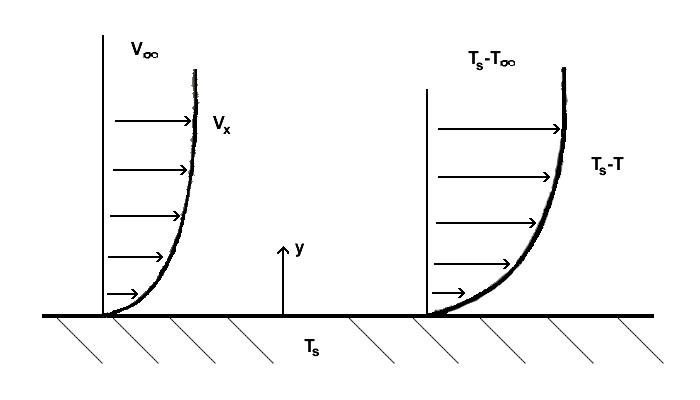
Понимание конвективных пограничных слоев необходимо для понимания конвективного теплопереноса между поверхностью и жидкостью, протекающей мимо нее. Тепловой пограничный слой образуется, если температура набегающего потока жидкости и температура поверхности различаются. Температурный профиль существует благодаря обмену энергией, возникающему в результате этой разницы температур.

Тепловой пограничный слой

Скорость теплопередачи можно записать с помощью закона охлаждения Ньютона как

$Q_{y}=hA\left(T_{s}-T_{\infty }\right)$,

где h — коэффициент теплопередачи , а A — площадь поверхности теплопередачи. Поскольку передача тепла на поверхности осуществляется за счет проводимости, ту же величину можно выразить через теплопроводность k :

$Q_{y}=-kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}$.

Эти два термина равны; таким образом

$-kA{\frac {\partial }{\partial y}}\left.\left(T-T_{s}\right)\right|_{y=0}=hA\left(T_{s}-T_{\infty }\right)$.

Перестановка,

${\frac {h}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\left(T_{s}-T_{\infty }\right)}}$.

Умножение на репрезентативную длину L дает безразмерное выражение:

${\frac {hL}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\frac {\left(T_{s}-T_{\infty }\right)}{L}}}$.

Правая часть теперь представляет собой отношение градиента температуры на поверхности к эталонному градиенту температуры, а левая часть аналогична модулю Био. Это становится отношением кондуктивного теплового сопротивления к конвективному тепловому сопротивлению жидкости, также известному как число Нуссельта, Nu.

$\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}$.

Вывод

Число Нуссельта можно получить путем безразмерного анализа закона Фурье , поскольку оно равно безразмерному градиенту температуры на поверхности:

$q=-kA\nabla T$, где q – скорость теплопередачи , k – постоянная теплопроводность и T жидкости – температура .

Действительно, если: $\nabla '=L\nabla$ и $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$

мы приходим к

$-\nabla 'T'={\frac {L}{kA(T_{h}-T_{c})}}q={\frac {hL}{k}}$

тогда мы определяем

$\mathrm {Nu} _{L}={\frac {hL}{k}}$

поэтому уравнение становится

$\mathrm {Nu} _{L}=-\nabla 'T'$

Интегрируясь по поверхности тела:

${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$,

где $S'={\frac {S}{L^{2}}}$.

Эмпирические корреляции

Обычно для свободной конвекции среднее число Нуссельта выражается как функция числа Рэлея и числа Прандтля и записывается как:

$\mathrm {Nu} =f(\mathrm {Ra} ,\mathrm {Pr} )$

В противном случае для принудительной конвекции число Нуссельта обычно является функцией числа Рейнольдса и числа Прандтля , или

$\mathrm {Nu} =f(\mathrm {Re} ,\mathrm {Pr} )$

эмпирические Доступны корреляции для самых разных геометрий, которые выражают число Нуссельта в вышеупомянутых формах.

Свободная конвекция

Свободная конвекция у вертикальной стены

Цитируется как исходило от Черчилля и Чу:

${\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.663\,\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{8}$

Свободная конвекция от горизонтальных пластин

Если характеристическая длина определена

$L\ ={\frac {A_{s}}{P}}$

где $\mathrm {A} _{s}$ - площадь поверхности пластины и $P$ это его периметр.

Затем для верхней поверхности горячего объекта в более холодной среде или нижней поверхности холодного объекта в более горячей среде.

${\overline {\mathrm {Nu} }}_{L}\ =0.54\,\mathrm {Ra} _{L}^{1/4}\,\quad 10^{4}\leq \mathrm {Ra} _{L}\leq 10^{7}$

${\overline {\mathrm {Nu} }}_{L}\ =0.15\,\mathrm {Ra} _{L}^{1/3}\,\quad 10^{7}\leq \mathrm {Ra} _{L}\leq 10^{11}$

И для нижней поверхности горячего объекта в более холодной среде или верхней поверхности холодного объекта в более горячей среде.

${\overline {\mathrm {Nu} }}_{L}\ =0.52\,\mathrm {Ra} _{L}^{1/5}\,\quad 10^{5}\leq \mathrm {Ra} _{L}\leq 10^{10}$

Свободная конвекция из шкафа с подогревом снизу

Цитируется как из Бежана:

${\overline {\mathrm {Nu} }}_{L}\ =0.069\,\mathrm {Ra} _{L}^{1/3}Pr^{0.074}\,\quad 3*10^{5}\leq \mathrm {Ra} _{L}\leq 7*10^{9}$

Это уравнение «выполняется, когдагоризонтальный слой достаточно широк, чтобы эффект коротких вертикальных сторонявляется минимальным».

Это было эмпирически определено Глоубом и Дропкиным в 1959 году: «Испытания проводились в цилиндрических контейнерах с медными верхом и дном и изолирующими стенками». Используемые контейнеры имели диаметр около 5 дюймов и высоту 2 дюйма.

Плоская пластина в ламинарном потоке

Локальное число Нуссельта для ламинарного течения над плоской пластиной на расстоянии $x$ ниже по течению от края пластины, определяется выражением

$\mathrm {Nu} _{x}\ =0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)$

Среднее число Нуссельта для ламинарного течения над плоской пластиной от края пластины до расстояния вниз по потоку. $x$, определяется

${\overline {\mathrm {Nu} }}_{x}\ ={2}\cdot 0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3}\ =0.664\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm {Pr} >0.6)$

Сфера в конвективном потоке

В некоторых приложениях, таких как испарение сферических капель жидкости в воздухе, используется следующая корреляция:

$\mathrm {Nu} _{D}\ ={2}+0.4\,\mathrm {Re} _{D}^{1/2}\,\mathrm {Pr} ^{1/3}\,$

Вынужденная конвекция в турбулентном потоке трубы

Корреляция Гнелинского

Соотношение Гнелинского для турбулентного течения в трубах:

$\mathrm {Nu} _{D}={\frac {\left(f/8\right)\left(\mathrm {Re} _{D}-1000\right)\mathrm {Pr} }{1+12.7(f/8)^{1/2}\left(\mathrm {Pr} ^{2/3}-1\right)}}$

где f — коэффициент трения Дарси , который можно получить либо из диаграммы Муди , либо для гладких трубок из корреляции, разработанной Петуховым:

$f=\left(0.79\ln \left(\mathrm {Re} _{D}\right)-1.64\right)^{-2}$

Корреляция Гнелинского справедлива для:

$0.5\leq \mathrm {Pr} \leq 2000$

$3000\leq \mathrm {Re} _{D}\leq 5\times 10^{6}$

Уравнение Диттуса – Бёлтера

Уравнение Диттуса-Бельтера (для турбулентного потока), введенное У.Х. Макадамсом. — явная функция для вычисления числа Нуссельта. Эту задачу легко решить, но она менее точна, если существует большая разница температур жидкости. Он предназначен для гладких труб, поэтому его использование для шероховатых труб (большинство коммерческих применений) рекомендуется с осторожностью. Уравнение Диттуса – Бёлтера:

$\mathrm {Nu} _{D}=0.023\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{n}$

где:

$D$ внутренний диаметр круглого воздуховода

$\mathrm {Pr}$ это число Прандтля

$n=0.4$ для нагреваемой жидкости, и $n=0.3$ для охлаждаемой жидкости.

Уравнение Диттуса–Бельтера справедливо для

$0.6\leq \mathrm {Pr} \leq 160$

$\mathrm {Re} _{D}\gtrsim 10\,000$

${\frac {L}{D}}\gtrsim 10$

Уравнение Диттуса-Бельтера является хорошим приближением, при котором разница температур между объемной жидкостью и поверхностью теплопередачи минимальна, что позволяет избежать сложности уравнения и итеративного решения. Берем воду со средней температурой объемной жидкости 20 °C (68 °F), вязкостью 10,07 × 10. ⁻⁴ Па·с и температура поверхности теплопередачи 40 °C (104 °F) (вязкость 6,96 × 10 ⁻⁴ Па.с , поправочный коэффициент вязкости для $({\mu }/{\mu _{s}})$ можно получить как 1,45. Это значение увеличивается до 3,57 при температуре поверхности теплопередачи 100 °C (212 °F) (вязкость 2,82 × 10 ⁻⁴ Па·с ), что существенно влияет на число Нуссельта и коэффициент теплопередачи.

Корреляция Зидера – Тейта

Корреляция Зидера-Тейта для турбулентного потока является неявной функцией , поскольку она анализирует систему как нелинейную краевую задачу . Результат Зидера-Тейта может быть более точным, поскольку он учитывает изменение вязкости ( $\mu$ и $\mu _{s}$) из-за изменения температуры между средней температурой объемной жидкости и температурой поверхности теплопередачи соответственно. Корреляция Зидера-Тейта обычно решается с помощью итерационного процесса, поскольку коэффициент вязкости будет меняться при изменении числа Нуссельта.

$\mathrm {Nu} _{D}=0.027\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{1/3}\left({\frac {\mu }{\mu _{s}}}\right)^{0.14}$

где:

$\mu$ вязкость жидкости при температуре объемной жидкости

$\mu _{s}$ - вязкость жидкости при температуре граничной поверхности теплопередачи

Корреляция Зидера-Тейта справедлива для

$0.7\leq \mathrm {Pr} \leq 16\,700$

$\mathrm {Re} _{D}\geq 10\,000$

${\frac {L}{D}}\gtrsim 10$

Вынужденная конвекция в полностью развитом ламинарном потоке трубы

Для полностью развитого внутреннего ламинарного течения числа Нуссельта стремятся к постоянному значению для длинных труб.

Для внутреннего потока:

$\mathrm {Nu} ={\frac {hD_{h}}{k_{f}}}$

где:

D _h = Гидравлический диаметр

k _f = теплопроводность жидкости

h = коэффициент конвективной теплопередачи

Конвекция с равномерной температурой для круглых трубок

От Incropera & DeWitt,

$\mathrm {Nu} _{D}=3.66$

Последовательность OEIS A282581 дает это значение как $\mathrm {Nu} _{D}=3.6567934577632923619...$.

Конвекция с равномерным тепловым потоком для круглых трубок

В случае постоянного поверхностного теплового потока

$\mathrm {Nu} _{D}=4.36$

См. также

• Число Шервуда (число массообмена Нуссельта)
• Уравнение Черчилля – Бернштейна
• Номер Биота
• Число Рейнольдса
• Конвективный теплообмен
• Коэффициент теплопередачи
• Теплопроводность

Внешние ссылки

• Простой вывод числа Нуссельта из закона охлаждения Ньютона (по состоянию на 23 сентября 2009 г.)
• ThermoTurb – Калькулятор коэффициентов теплопередачи