Степень (угол)
| Степень | |
|---|---|
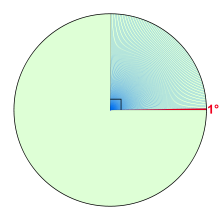 Один градус (показан красным) и восемьдесят девять градусов (показан синим). Обведенная область представляет собой прямой угол . | |
| Общая информация | |
| Система единиц | Не принятая единица SI |
| Единица | Угол |
| Символ | ° [1] [2] , ты [3] |
| Конверсии | |
| 1° [1] [2] в ... | ... равно... |
| поворачивается | 1/360 поворот |
| радианы | π / 180 рад ≈ 0,01745.. рад |
| миллирадианы | 50· π / 9 мрад ≈ 17,45.. мрад |
| гул | 10 / 9 г |
Градус или (полностью градус дуги , градус дуги градус дуги ), обычно обозначаемый ° ( символ градуса ), представляет собой измерение плоского угла , при котором один полный оборот составляет 360 градусов. [4]
Это не единица СИ — единицей угловой меры СИ является радиан , — но она упоминается в брошюре СИ как принятая единица . [5] Поскольку полный оборот равен 2 π радиан, один градус эквивалентен π / 180 радиан.
История
[ редактировать ]
Первоначальная мотивация выбора градуса как единицы вращения и угла неизвестна. Одна теория утверждает, что это связано с тем фактом, что 360 — это примерно количество дней в году. Древние астрономы заметили, что Солнце, которое эклиптики в течение года следует по траектории , кажется, продвигается по своему пути примерно на один градус каждый день. Некоторые древние календари , такие как персидский календарь и вавилонский календарь , использовали 360 дней в году. Использование календаря на 360 дней может быть связано с использованием шестидесятеричных чисел. [4]
Другая теория состоит в том, что вавилоняне разделили круг, используя угол равностороннего треугольника в качестве основной единицы, а затем разделили последний на 60 частей, следуя своей шестидесятеричной системе счисления. [7] [8] Самая ранняя тригонометрия , использовавшаяся вавилонскими астрономами и их греческими преемниками, была основана на хордах окружности. Хорда длиной, равной радиусу, представляет собой естественную базовую величину. Одна шестидесятая часть этого числа, если использовать стандартное шестидесятеричное деление, составляла степень.
Аристарх Самосский и Гиппарх, похоже, были одними из первых греческих ученых, систематически использовавших вавилонские астрономические знания и методы. [9] [10] Тимохарис , Аристарх, Аристилл , Архимед и Гиппарх были первыми греками, которые, как известно, разделили круг на 360 градусов по 60 угловых минут . [ нужна ссылка ] Эратосфен использовал более простую шестидесятеричную систему, делящую круг на 60 частей. [ нужна ссылка ]
Другой причиной выбора числа 360 могло быть то, что оно легко делится : у 360 24 делителя . [примечание 1] что делает его одним из семи чисел, так что ни одно число, меньшее чем в два раза, не имеет больше делителей (последовательность A072938 в OEIS ). [11] Кроме того, оно делится на все числа от 1 до 10, кроме 7. [примечание 2] Это свойство имеет множество полезных применений, например, деление мира на 24 часовых пояса , каждый из которых номинально составляет 15° долготы , для соответствия установленному 24-часовому сутку .
Наконец, может случиться так, что в игру вступил более чем один из этих факторов. Согласно этой теории, это число составляет примерно 365 из-за кажущегося движения Солнца относительно небесной сферы, и оно было округлено до 360 по некоторым математическим причинам, упомянутым выше.
Подразделения
[ редактировать ]Для многих практических целей градус — это достаточно маленький угол, чтобы целые градусы обеспечивали достаточную точность. Когда это не так, как в астрономии или для географических координат ( широта и долгота ), градусные измерения могут быть записаны с использованием десятичных градусов ( нотация DD ); например, 40,1875°.
В качестве альтернативы можно использовать традиционные шестидесятеричные единицы деления: один градус делится на 60 минут (угловых) , а одна минута - на 60 секунд (угловых) . Использование градусов-минут-секунд также называется обозначением DMS . Эти подразделения, также называемые угловой минутой и угловой секундой , представлены одинарным штрихом (′) и двойным штрихом (″) соответственно. Например, 40,1875° = 40° 11′ 15″ . Дополнительную точность можно обеспечить, используя десятичные доли угловой секунды.
Морские карты отмечены в градусах и десятичных минутах для облегчения измерений; 1 минута широты равна 1 морской миле . В приведенном выше примере будет 40° 11,25’ (обычно пишется как 11’25 или 11’,25). [12]
Более старая система третей , четвертей и т. д., продолжающая шестидесятеричную систему деления, использовалась аль-Каши. [ нужна ссылка ] и других древних астрономов, но сегодня используется редко. Эти подразделения обозначались путем написания римской цифры числа шестидесятых в верхнем индексе: 1. я для « простого числа » (угловой минуты) 1 II на секунду , 1 III за треть , 1 IV за четвертого и т. д. [13] Следовательно, современные символы минуты и секунды дуги, а также слово «секунда» также относятся к этой системе. [14]
Префиксы SI также могут применяться, например, миллиградусы , микроградусы и т. д.
Альтернативные единицы
[ редактировать ]
В большинстве математических работ, выходящих за рамки практической геометрии, углы обычно измеряются в радианах, а не в градусах. Это происходит по разным причинам; например, тригонометрические функции имеют более простые и «естественные» свойства, когда их аргументы выражены в радианах. Эти соображения перевешивают удобную делимость числа 360. Один полный оборот (360°) равен 2 π радианам, поэтому 180° равны π радианам, или, что то же самое, степень является математической константой : 1° = π ⁄ 180 .
Один оборот (соответствующий циклу или обороту) равен 360°.
С изобретением метрической системы , основанной на степенях десяти, во Франции и близлежащих странах была предпринята попытка замены градусов десятичными «градусами». [примечание 3] где число в прямом углу равно 100 гон, а в полном круге 400 гон (1° = 10/9 гон . ) Это называлось грейд (нуво) или град . Из-за путаницы с существующим термином grad(e) в некоторых странах Северной Европы (что означает стандартную степень, 1/360 на ( оборота), новая единица называлась Neugrad ( немецком языке тогда как «старая» степень называлась Altgrad ), аналогично nygrad на датском , шведском и норвежском языках также gradian ), и nýgráða на исландском языке . название «Гон» Чтобы положить конец путанице, позже для нового подразделения было принято . Хотя Наполеон отказался от этой идеи метрификации, оценки продолжали использоваться в нескольких областях, и их поддерживают многие научные калькуляторы . Дециградирует ( 1/4000 . войну ) использовались с французскими артиллерийскими прицелами в Первую мировую
Угловой мил , который чаще всего используется в военных целях, имеет как минимум три конкретных варианта: от 1 ⁄ 6400 до 1 ⁄ 6000 . Он примерно равен одному миллирадиану ( ок. 1 / 6,283 ). Мил измерения 1/6000 . , революции зародилось в императорской русской армии где равносторонняя хорда делилась на десятые, чтобы дать круг в 600 единиц Это можно увидеть на подкладочном самолете (раннем устройстве для наведения артиллерийского огня с закрытых позиций ), датируемом примерно 1900 годом в Санкт-Петербургском Артиллерийском музее.
| Повороты | радианы | Степени | Градианы |
|---|---|---|---|
| 0 ход | 0 рад | 0° | 0 г |
| 1/72 поворота | π / 36 рад | 5° | 5 + 5 / 9 г |
| 1/24 поворота | π / 12 рад | 15° | 16 + 2 / 3 г |
| 1/16 поворот | π / 8 рад | 22.5° | 25 г |
| 1/12 поворот | π / 6 рад | 30° | 33 + 1 / 3 г |
| 1/10 поворот | π / 5 рад | 36° | 40 г |
| 1/8 поворота | π / 4 рад | 45° | 50 г |
| 1/2 τ π или поворот | 1 рад | ок. 57,3° | ок. 63,7 г |
| 1 / 6 поворот | π / 3 рад | 60° | 66 + 2 / 3 г |
| 1/5 поворот | 2 π или τ / 5 рад | 72° | 80 г |
| 1/4 поворота | π / 2 рад | 90° | 100 г |
| 1/3 поворота | 2 π или τ / 3 рад | 120° | 133 + 1 / 3 г |
| 2 / 5 поворот | 4 π или α / 5 рад | 144° | 160 г |
| 1/2 поворота | п рад | 180° | 200 г |
| 3 / 4 поворот | 3 π или ρ / 2 рад | 270° | 300 г |
| 1 ход | т или 2 п рад | 360° | 400 г |
См. также
[ редактировать ]- Компас
- Степень кривизны
- Градусов в секунду
- Географическая система координат
- Градиан
- Меридианная дуга
- Квадратный градус
- Квадратная минута
- Квадратная секунда
- стерадиан
Примечания
[ редактировать ]- ^ Делители числа 360: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360.
- ^ Сравните это с относительно громоздким числом 2520 , которое является наименьшим общим кратным для каждого числа от 1 до 10.
- ^ Эти новые десятичные «градусы» не следует путать с десятичными градусами .
Ссылки
[ редактировать ]- ^ HP Series 48G – Руководство пользователя (UG) (8-е изд.). Хьюлетт-Паккард . Декабрь 1994 г. [1993]. HP 00048-90126, (00048-90104) . Проверено 6 сентября 2015 г.
- ^ Руководство пользователя графического калькулятора HP 50g (UG) (1-е изд.). Хьюлетт-Паккард . 1 апреля 2006 г. HP F2229AA-90006 . Проверено 10 октября 2015 г.
- ^ Руководство пользователя графического калькулятора HP Prime (UG) (PDF) (1-е изд.). Hewlett-Packard Development Company, LP , октябрь 2014 г. HP 788996-001. Архивировано из оригинала (PDF) 3 сентября 2014 года . Проверено 13 октября 2015 г.
- ^ Перейти обратно: а б Вайсштейн, Эрик В. «Степень» . mathworld.wolfram.com . Проверено 31 августа 2020 г.
- ^ Международное бюро мер и весов , Международная система единиц (СИ) / Международная система единиц (СИ) , 9-е изд. [ постоянная мертвая ссылка ] (Севр: 2019 г.), ISBN 978-92-822-2272-0 , гр. 4, стр. 145–146.
- ^ Евклид (2008). «Книга 4». Элементы геометрии Евклида [ Euclidis Elementa, editit et Latin Interpatus est IL Heiberg, в aedibus BG Teubneri 1883–1885 ]. Перевод Хейберга, Йохана Людвига ; Фитцпатрик, Ричард (2-е изд.). Издательство Принстонского университета . ISBN 978-0-6151-7984-1 . [1]
- ^ Джинсы, Джеймс Хопвуд (1947). Рост физической науки . Издательство Кембриджского университета (CUP). п. 7 .
- ^ Мурнаган, Фрэнсис Доминик (1946). Аналитическая геометрия . п. 2.
- ^ Роулинз, Деннис. «Об Аристархе» . ДИО — Международный журнал научной истории .
- ^ Тумер, Джеральд Джеймс . Гиппарх и вавилонская астрономия .
- ^ Брефельд, Вернер. « Делимость весьма сложных чисел» (на немецком языке).
- ^ Хопкинсон, Сара (2012). Справочник шкипера RYA - парус . Хэмбл: Королевская яхтенная ассоциация . п. 76. ИСБН 9781-9051-04949 .
- ^ Аль-Бируни (1879) [1000]. Хронология древних народов . Перевод Сахау, К. Эдварда. стр. 147–149.
- ^ Флегг, Грэм Х. (1989). Числа сквозь века . Международное высшее образование Макмиллана . стр. 156–157. ISBN 1-34920177-4 .
Внешние ссылки
[ редактировать ]- «Градусы как мера угла» . , с интерактивной анимацией
- Грей, Меган; Меррифилд, Майкл; Мориарти, Филип (2009). «° Степень угла» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .