Профиль

Примеры аэродинамических профилей в природе и на различных транспортных средствах. Плавник дельфина внизу слева подчиняется тем же принципам в другой жидкой среде; это пример судна на подводных крыльях .

Продолжительность: 1 минута 54 секунды. 1:54

Линии обтекаемости профиля, визуализированные с помощью дымовой аэродинамической трубы

Аэродинамический профиль ( американский английский ) или аэродинамический профиль ( британский английский ) — это обтекаемое тело, способное создавать значительно большую подъемную силу, чем сопротивление . Крылья, паруса и лопасти винта являются примерами аэродинамических профилей. Крылья аналогичной функции, в которых в качестве рабочей жидкости используется вода, называются подводными крыльями .

При ориентации под подходящим углом твердое тело, движущееся через жидкость, отклоняет встречную жидкость (для самолетов - нисходящую силу), в результате чего на крыло действует сила в направлении, противоположном отклонению. Эта сила известна как аэродинамическая сила и может быть разделена на две составляющие: подъемная сила ( перпендикулярная потока скорости набегающего ) и сопротивление ( параллельное скорости набегающего потока).

Подъемная сила профиля в первую очередь зависит от угла атаки . Большинству форм крыла для создания подъемной силы требуется положительный угол атаки, но изогнутые крылья могут создавать подъемную силу при нулевом угле атаки. Профили аэродинамических профилей можно спроектировать для использования на разных скоростях, изменив их геометрию: профили для дозвуковых полетов обычно имеют закругленную переднюю кромку , а те, которые предназначены для сверхзвуковых полетов, имеют тенденцию быть тоньше и с острой передней кромкой. Все они имеют острую заднюю кромку.

Воздух, отклоняемый аэродинамическим профилем, заставляет его создавать «тень» с более низким давлением над собой и позади себя. Эта разница давлений сопровождается разницей скоростей в соответствии с принципом Бернулли , поэтому результирующее поле потока вокруг аэродинамического профиля имеет более высокую среднюю скорость на верхней поверхности, чем на нижней поверхности. В некоторых ситуациях (например, невязкий потенциальный поток ) подъемная сила может быть напрямую связана со средней разницей скоростей верхней и нижней части без вычисления давления с использованием концепции циркуляции и теоремы Кутты-Жуковского .

Обзор

Обтекает профиль NACA 0012 при умеренном угле атаки.

Кривые подъема и сопротивления для типичного профиля крыла

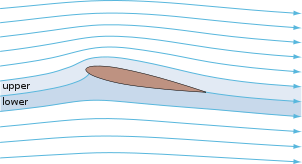
Крылья и стабилизаторы самолетов , а также лопасти винтов вертолетов имеют поперечное сечение аэродинамической формы. Аэродинамические профили также встречаются в пропеллерах, вентиляторах , компрессорах и турбинах . Паруса также являются аэродинамическими профилями, а подводные поверхности парусников, такие как шверт , руль направления и киль , схожи по поперечному сечению и действуют по тем же принципам, что и аэродинамические профили. Плавающие и летающие существа и даже многие растения и сидячие организмы используют аэродинамические крылья/подводные крылья: распространенными примерами являются крылья птиц, тела рыб и форма песчаных долларов . Крыло в форме аэродинамического профиля может создавать прижимную силу на автомобиле или другом транспортном средстве, улучшая тягу .

Когда ветру препятствует такой объект, как плоская плита, здание или настил моста, объект будет испытывать сопротивление , а также аэродинамическую силу, перпендикулярную ветру. Это не означает, что объект квалифицируется как аэродинамический профиль. Аэродинамические профили представляют собой высокоэффективные подъемные формы, способные создавать большую подъемную силу, чем плоские пластины аналогичного размера и той же площади, и способны создавать подъемную силу со значительно меньшим сопротивлением. Профили используются при проектировании самолетов, пропеллеров, лопастей несущего винта, ветряных турбин и других приложений авиационной техники.

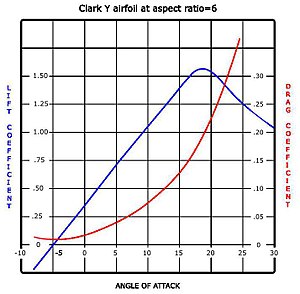
Кривая подъемной силы и сопротивления, полученная при испытаниях в аэродинамической трубе, показана справа. Кривая представляет собой профиль с положительным развалом, поэтому при нулевом угле атаки создается некоторая подъемная сила. С увеличением угла атаки подъемная сила увеличивается примерно в линейной зависимости, называемой наклоном кривой подъемной силы. Примерно при 18 градусах этот профиль глохнет, и после этого подъемная сила быстро падает. Падение подъемной силы можно объяснить действием пограничного слоя верхней поверхности , который отделяется и сильно утолщается над верхней поверхностью при угле сваливания и за его пределами. утолщенного пограничного слоя Толщина смещения изменяет эффективную форму профиля, в частности, уменьшает его эффективный изгиб , что изменяет общее поле потока, уменьшая циркуляцию и подъемную силу. Более толстый пограничный слой также приводит к значительному увеличению сопротивления давления , так что общее сопротивление резко увеличивается вблизи точки срыва и после нее.

Конструкция аэродинамического профиля является важным аспектом аэродинамики . Различные профили предназначены для разных режимов полета. Асимметричные профили могут создавать подъемную силу при нулевом угле атаки, тогда как симметричный профиль лучше подходит для частых перевернутых полетов, например, на пилотажном самолете. В районе элеронов и возле законцовки крыла можно использовать симметричный профиль для увеличения диапазона углов атаки штопора предотвращения и . Таким образом, можно использовать широкий диапазон углов без разделения пограничного слоя . Дозвуковые профили имеют круглую переднюю кромку, которая, естественно, нечувствительна к углу атаки. Однако поперечное сечение не является строго круглым: радиус кривизны увеличивается до того, как крыло достигнет максимальной толщины, чтобы минимизировать вероятность отрыва пограничного слоя. Это удлиняет крыло и смещает точку максимальной толщины назад от передней кромки.

Сверхзвуковые профили имеют гораздо более угловатую форму и могут иметь очень острую переднюю кромку, которая очень чувствительна к углу атаки. Сверхкритический профиль имеет максимальную толщину вблизи передней кромки и имеет большую длину, чтобы медленно возвращать сверхзвуковой поток до дозвуковых скоростей. Обычно такие трансзвуковые профили, а также сверхзвуковые профили имеют небольшой развал, чтобы уменьшить расхождение лобового сопротивления . Крылья современных самолетов могут иметь разные секции профиля по размаху крыла, каждая из которых оптимизирована для условий в каждой секции крыла.

Подвижные механизаторы, закрылки , а иногда и предкрылки , установлены на крыльях почти каждого самолета. Закрылок задней кромки действует аналогично элеронам; однако его, в отличие от элеронов, можно частично убрать в крыло, если он не используется.

Крыло с ламинарным обтеканием имеет максимальную толщину в средней линии развала. Анализ уравнений Навье–Стокса в линейном режиме показывает, что отрицательный градиент давления вдоль потока оказывает тот же эффект, что и уменьшение скорости. Так что при максимальном развале посередине возможно поддержание ламинарного обтекания большей части крыла на более высокой крейсерской скорости. Однако некоторое поверхностное загрязнение нарушит ламинарный поток, сделав его турбулентным. Например, при дожде на крыле поток будет турбулентным. При определенных условиях остатки насекомых на крыле также могут вызвать потерю небольших участков ламинарного потока. До исследований НАСА в 1970-х и 1980-х годах сообщество разработчиков самолетов из попыток применения в эпоху Второй мировой войны поняло, что конструкции крыльев с ламинарным потоком непрактичны с использованием общих производственных допусков и дефектов поверхности. Это мнение изменилось после того, как были разработаны новые методы производства с использованием композитных материалов (например, аэродинамические профили с ламинарным потоком, разработанные профессором Францем Вортманном для использования с крыльями из армированного волокном пластика ). Были также внедрены методы механической обработки металла. Исследования НАСА в 1980-х годах выявили практичность и полезность конструкций крыльев с ламинарным потоком и открыли путь для применения ламинарного потока на современных практических поверхностях самолетов, от дозвуковых самолетов гражданской авиации до трансзвуковых больших транспортных самолетов и сверхзвуковых конструкций.

Были разработаны схемы для определения аэродинамических профилей — примером является система NACA . Также используются различные системы формирования профиля. Примером профиля профиля общего назначения, который находит широкое применение и предшествует системе NACA, является Clark-Y . Сегодня аэродинамические профили можно проектировать для выполнения определенных функций с помощью компьютерных программ.

Терминология аэродинамического профиля

Номенклатура профиля крыла

Ниже даны определения различных терминов, связанных с аэродинамическими профилями:

• Поверхность всасывания (также известная как верхняя поверхность) обычно связана с более высокой скоростью и более низким статическим давлением.
• Поверхность давления (также известная как нижняя поверхность) имеет сравнительно более высокое статическое давление, чем поверхность всасывания. Градиент давления между этими двумя поверхностями способствует созданию подъемной силы, создаваемой данным профилем.

Геометрия профиля описывается различными терминами:

• Передняя кромка — это точка в передней части профиля, имеющая максимальную кривизну (минимальный радиус).
• — Задняя кромка это точка профиля, наиболее удаленная от передней кромки. Угол между верхней и нижней поверхностями задней кромки является углом задней кромки .
• Хорда . – это прямая линия, соединяющая переднюю и заднюю кромки Длина хорды , или просто хорды , $c$, — длина хорды. Это базовый размер сечения аэродинамического профиля.

Различные определения толщины профиля.

Профиль для винглетов (PSU 90-125WL)

Форма профиля определяется с использованием следующих геометрических параметров:

• Средняя линия развала или средняя линия — это геометрическое положение точек на полпути между верхней и нижней поверхностями. Его форма зависит от распределения толщины по хорде;
• Толщина . профиля меняется вдоль хорды Его можно измерить одним из двух способов:
  • Толщина измеряется перпендикулярно линии развала. Иногда это называют «американской конвенцией»;
  • Толщина измеряется перпендикулярно линии хорды. Иногда это называют «Британской конвенцией».

Некоторыми важными параметрами для описания формы аэродинамического профиля являются его выпуклость и толщина . Например, профиль 4-значной серии NACA, такой как NACA 2415 (читается как 2–4–15), описывает профиль с выпуклостью хорды 0,02, расположенный на хорде 0,40, с хордой максимальной толщины 0,15.

Наконец, важными понятиями, используемыми для описания поведения профиля при движении через жидкость, являются:

• Аэродинамический центр , который представляет собой положение по хорде, относительно которого момент тангажа не зависит от коэффициента подъемной силы и угла атаки.
• Центр давления , который является местом по хорде, вокруг которого момент тангажа на мгновение равен нулю. На изогнутом профиле центр давления не является фиксированным, поскольку он перемещается в ответ на изменения угла атаки и коэффициента подъемной силы.

При двумерном обтекании однородного крыла бесконечного размаха наклон кривой подъемной силы определяется в первую очередь углом задней кромки . Наклон наибольший, если угол равен нулю; и уменьшается с увеличением угла. Для крыла конечного размаха удлинение крыла также существенно влияет на наклон кривой. По мере уменьшения соотношения сторон наклон также уменьшается.

Теория тонкого профиля

На законцовке самолета Денни Китфокс , построенного в 1991 году, видна часть профиля крыла.

Профиль Ка-26. нижней лопасти вертолета

Теория тонкого профиля — это простая теория профиля, которая связывает угол атаки с подъемной силой для несжимаемых, невязких потоков . Он был разработан немецким математиком Максом Мунком и усовершенствован британским аэродинамиком Германом Глауэртом и другими. в 1920-е годы. Теория идеализирует обтекание профиля как двумерное обтекание тонкого профиля. Это можно представить как обращение к аэродинамическому профилю нулевой толщины и бесконечному размаху крыльев .

Теория тонкого профиля была особенно примечательна в свое время, поскольку она обеспечила прочную теоретическую основу для следующих важных свойств профилей в двумерном невязком потоке:

1. на симметричном профиле центр давления и аэродинамический центр совпадают и лежат ровно на четверть хорды позади передней кромки.
2. на изогнутом профиле аэродинамический центр лежит ровно на четверть хорды позади передней кромки, но положение центра давления перемещается при изменении угла атаки.
3. наклон коэффициента подъемной силы в зависимости от угла линии атаки равен $2\pi \!$ единиц на радиан.

Как следствие (3), коэффициент подъемной силы сечения тонкого симметричного профиля бесконечного размаха крыла равен:

$\ c_{l}=2\pi \alpha$

где $c_{l}\!$ - коэффициент подъемной силы секции,

$\alpha \!$ — угол атаки в радианах, измеренный относительно линии хорды .

(Вышеупомянутое выражение также применимо к изогнутому аэродинамическому профилю, где $\alpha \!$ — угол атаки, измеренный относительно линии нулевой подъемной силы, а не линии хорды.)

Кроме того, как следствие (3), коэффициент подъемной силы сечения изогнутого профиля крыла бесконечного размаха составляет:

$\ c_{l}=c_{l_{0}}+2\pi \alpha$

где $\ c_{l_{0}}$ – коэффициент подъемной силы секции при угле атаки, равном нулю.

Теория тонкого профиля предполагает, что воздух представляет собой невязкую жидкость , поэтому не учитывает срыв профиля, который обычно происходит при угле атаки от 10 ° до 15 ° для типичных профилей. Однако в середине-конце 2000-х годов Уоллес Дж. Моррис II в своей докторской диссертации предложил теорию, предсказывающую возникновение срыва на переднем крае. Последующие уточнения Морриса содержат подробности текущего состояния теоретических знаний о феномене срыва на переднем крае. Теория Морриса предсказывает критический угол атаки для начала срыва передней кромки как условие, при котором в решении для внутреннего потока прогнозируется глобальная зона отрыва. Теория Морриса показывает, что дозвуковое обтекание тонкого профиля можно описать как внешнюю область вокруг большей части хорды профиля и внутреннюю область вокруг носовой части, которые асимптотически соответствуют друг другу. Поскольку течение во внешней области определяется классической теорией тонкого профиля, уравнения Морриса демонстрируют многие компоненты теории тонкого профиля.

Вывод

Сверху вниз: * Профиль с ламинарным потоком для флаера парка радиоуправления Профиль с * ламинарным потоком для пилота с пилоном на радиоуправлении * Профиль с ламинарным потоком для винтокрылого самолета с экипажем * Ламинарный профиль на профиле реактивного авиалайнера * Стабильный профиль, используемый для летающих крыльев * Загруженная корма профиль, позволяющий использовать большой основной лонжерон и позднее сваливание * Трансзвуковой сверхкритический профиль * Сверхзвуковой профиль передней кромки

  ламинарный поток

  турбулентный поток

  дозвуковой поток

  объем сверхзвукового потока

В теории тонкого профиля ширина (2D) профиля предполагается незначительной, а сам профиль заменяется лопастью 1D вдоль линии его развала, ориентированной под углом атаки α . Пусть положение вдоль лопасти будет x в диапазоне от 0 в передней части крыла до c на задней кромке; развал аэродинамического профиля, dy ⁄ dx предполагается достаточно малым, поэтому нет необходимости различать x и положение относительно фюзеляжа.

Поток через профиль создает циркуляцию вокруг лопасти, которую можно смоделировать как вихревой лист с изменяющейся в положении силой γ( x ) . Условие Кутты подразумевает, что γ( c )=0 , но прочность сингулярна на передней части лезвия, причем γ( x )∝ 1 ⁄ √ Икс для Икс ≈ 0 . Если основной поток V имеет плотность ρ , то по теореме Кутты–Жуковского общая подъемная сила F пропорциональна $$\rho V\int _{0}^{c}\gamma (x)\,dx$$и его момент M относительно передней кромки, пропорциональный $$\rho V\int _{0}^{c}x\;\gamma (x)\,dx.$$

Согласно закону Био-Савара , завихренность γ( x ) создает поле течения $$w(x)={\frac {1}{2\pi }}\int _{0}^{c}{\frac {\gamma (x')}{x-x'}}\,dx'{\text{,}}$$ ориентирован нормально к профилю в точке x . Поскольку профиль представляет собой непроницаемую поверхность , поток $w(x)$ должен уравновешивать обратный поток от V . В малоугловом приближении V наклонена под углом α- dy / dx относительно лопасти в положении x , а нормальная составляющая соответственно (α- dy ⁄ dx ) V . Таким образом, γ( x ) должно удовлетворять свертки уравнению $$\left(\alpha -{\frac {dy}{dx}}\right)V=-w(x)=-{\frac {1}{2\pi }}\int _{0}^{c}{\frac {\gamma (x')}{x-x'}}\,dx'{\text{,}}$$ что однозначно определяет его в терминах известных величин.

Явное решение можно получить, сначала заменив переменные $$x=c\cdot {\frac {1+\cos(\theta )}{2}},$$а затем расширяя оба dy ⁄ dx и γ( x ) как безразмерный ряд Фурье по θ с измененным ведущим членом: $${\begin{aligned}&{\frac {dy}{dx}}=A_{0}+A_{1}\cos(\theta )+A_{2}\cos(2\theta )+\dots \\&\gamma (x)=2(\alpha +A_{0})\left({\frac {\sin \theta }{1+\cos \theta }}\right)+2A_{1}\sin(\theta )+2A_{2}\sin(2\theta )+\dots {\text{.}}\end{aligned}}$$ Результирующая подъемная сила и момент зависят только от первых нескольких членов этого ряда.

Коэффициент подъемной силы удовлетворяет $$C_{L}=2\pi \left(\alpha +A_{0}+{\frac {A_{1}}{2}}\right)=2\pi \alpha +2\int _{0}^{\pi }{{\frac {dy}{dx}}\cdot (1+\cos \theta )\,d\theta }$$ и коэффициент момента $$C_{M}=-{\frac {\pi }{2}}\left(\alpha +A_{0}+A_{1}-{\frac {A_{2}}{2}}\right)=-{\frac {\pi }{2}}\alpha -\int _{0}^{\pi }{{\frac {dy}{dx}}\cdot \cos(\theta )(1+\cos \theta )\,d\theta }{\text{.}}$$ Таким образом, момент относительно точки 1/4 хорды будет равен $$C_{M}(1/4c)=-\pi /4(A_{1}-A_{2}){\text{.}}$$ Отсюда следует, что центр давления находится позади точки «четверть хорды» на 0,25 с , на $$\Delta x/c=\pi /4((A_{1}-A_{2})/C_{L}){\text{.}}$$ Аэродинамическим центром называется положение, при котором момент тангажа М ' не изменяется при изменении коэффициента подъемной силы: $${\frac {\partial (C_{M'})}{\partial (C_{L})}}=0{\text{.}}$$ Теория тонкого профиля показывает, что в двумерном невязком потоке аэродинамический центр находится в положении четверти хорды.

См. также

• Крыло контроля циркуляции
• Судно на подводных крыльях
• Профиль Клайна – Фоглемана
• Эффект Кюсснера
• Парафойл
• Конфигурация крыла

Ссылки

Общие источники

• Эбботт, Ира Герберт ; Фон Дёнхофф, Альберт Эдвард (1959). Теория сечений крыла, включая сводные данные о профиле крыла . Дувр. ISBN  978-0-486-60586-9 .
• Олд, Дуглас; Шринивас (1995). «Теория двумерного тонкого аэродинамического профиля» . Аэродинамика для студентов . Университет Сиднея.
• Бабинский, Хольгер (ноябрь 2003 г.). «Как работают крылья?» (PDF) . Физическое образование . 38 (6): 497–503. Бибкод : 2003PhyEd..38..497B . дои : 10.1088/0031-9120/38/6/001 . S2CID   1657792 .
• Бэтчелор, Джордж. К (1967). Введение в гидродинамику . Кембриджский университет. стр. 467–471.
• Бертин, Джон Дж.; Каммингс, Рассел М. (2009). Аэродинамика для инженеров (5-е изд.). Пирсон Прентис Холл. ISBN  978-0-13-227268-1 .
• Клэнси, ЖЖ (1975). Аэродинамика . Лондон: Питман. ISBN  0-273-01120-0 .
• Холлидей, Дэвид; Резник, Роберт (1988). Основы физики (3-е изд.). Джон Уайли и сыновья.
• Хоутон, Эл.; Карпентер, П.В.; Колликотт, Стивен Х.; Валентин, Дэниел (2012). Аэродинамика для студентов-инженеров (6-е изд.). Эльзевир. ISBN  978-0-08-096633-5 .
• Моррис, Уоллес Дж. II (2009). Универсальный прогноз начала сваливания аэродинамических профилей в широком диапазоне чисел Рейнольдса (доктор философии). Гарвардский университет. Бибкод : 2009PhDT.......146M .
• Моррис, Уоллес Дж.; Русак, Цви (октябрь 2013 г.). «Начало сваливания на аэродинамических крыльях при потоках числа Рейнольдса от низкого до умеренно высокого». Журнал механики жидкости . 733 : 439–472. Бибкод : 2013JFM...733..439M . дои : 10.1017/jfm.2013.440 . ISSN   0022-1120 . S2CID   122817884 .
• Филлипс, Уоррен Ф. (2004). Механика полета . Джон Уайли и сыновья. ISBN  978-0-471-33458-3 .
• Скотт, Джефф (10 августа 2003 г.). «Вопрос № 136: Коэффициент подъемной силы и теория тонкого профиля» . Спросите ученого-ракетчика: Аэродинамика. Aerospaceweb.org.
• Трауб, Лэнс В. (24 марта 2016 г.). «Полуэмпирический прогноз гистерезиса профиля» . Аэрокосмическая промышленность . 3 (2): 9. Бибкод : 2016Аэрос...3....9Т . doi : 10.3390/aerospace3020009 .
• Вельтнер, Клаус; Ингельман-Сундберг, Мартин (1999). «Физика полета – еще раз» . Архивировано из оригинала 29 сентября 2011 года . Проверено 25 апреля 2021 г.

Дальнейшее чтение

• Андерсон, Джон, Д. (2007). Основы аэродинамики . МакГроу-Хилл. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Али Камранпай, Алиреза Мехрабади. Численный анализ профиля NACA 0012 при различных углах атаки и получение его аэродинамических коэффициентов. Журнал мехатроники и автоматизации. 2019 год; 6(3): 8–16п.
• Бирман, Мэтт (2019). «Плыть по течению? Вклад Великобритании в исследования ламинарного потока, 1930–1947». Историк авиации (29): 74–87. ISSN   2051-1930 .

Внешние ссылки

• База данных координат профилей UIUC
• Эталонное приложение для аэродинамических и подводных крыльев
• FoilSim Симулятор аэродинамического профиля от НАСА.
• Детская площадка с аэродинамическим профилем — интерактивное веб-приложение
• Десктопаэро
• Воздушный поток через крыло (Кембриджский университет)