Список правильных многогранников
В этой статье перечислены соединения правильных многогранников в евклидовом, сферическом и гиперболическом пространствах.
Двумерные соединения
[ редактировать ]Для любого натурального числа n существуют n-лучевые правильные многоугольные звезды с символами Шлефли {n/m} для всех m такие, что m < n/2 (строго говоря, {n/m}={n/(n−m) }) и m и n взаимно просты . Если m и n не являются взаимно простыми, полученный звездчатый многоугольник будет правильным многоугольником с n / m сторонами. Новую фигуру получают поворотом этих правильных n / m -угольников на одну вершину влево в исходном многоугольнике до тех пор, пока количество повернутых вершин не станет равно n / m минус одна, и объединением этих фигур. Крайним случаем является случай, когда n / m равно 2, что дает фигуру, состоящую из n /2 отрезков прямой; это называется вырожденным звездчатым многоугольником .
В других случаях, когда n и m звездчатый многоугольник для меньшего n имеют общий коэффициент, получается , и повернутые версии могут быть объединены. Эти фигуры называются звездчатыми фигурами , неправильными звездчатыми многоугольниками или составными многоугольниками . Для них часто используется одно и то же обозначение { n / m }, хотя такие авторитеты, как Грюнбаум (1994), считают (с некоторым обоснованием) форму k { n } более правильной, где обычно k = m .
Дальнейшее усложнение возникает, когда мы соединяем два или более звездчатых многоугольника, как, например, две пентаграммы, отличающиеся поворотом на 36°, вписанные в десятиугольник. Это правильно записывается в форме k { n / m }, как 2{5/2}, а не как обычно используемый {10/4}.
Расширенное обозначение Коксетера для соединений имеет форму c { m , n ,...}[ d { p , q ,...}] e { s , t ,...}, что указывает на то, что d различные { p , q ,...} вместе покрывают вершины { m , n ,...} c раз и грани { s , t ,...} e раз. Если регулярных { m , n ,...} не существует, первая часть обозначения удаляется, остается [ d { p , q ,...}] e { s , t ,...}; обратное справедливо, если регулярных { s , t ,...} не существует. Двойственным к c { m , n ,...}[ d { p , q ,...}] e { s , t ,...} является e { t , s ,...}[ d { q , p ,...}] c { n , m ,...}. Если c или e равны 1, их можно опустить. Для составных многоугольников это обозначение сводится к { nk }[ k { n / m }]{ nk }: например, гексаграмму можно записать так: {6}[2{3}]{6}.
 2{2} |
3{2} |
 4{2} |
5{2} |
 6{2} |
7{2} |
 8{2} |
9{2} |
 10{2} |
 11{2} |
 12{2} |
 13{2} |
 14{2} |
 15{2} | |
2{3} |
 3{3} |
 4{3} |
 5{3} |
6{3} |
 7{3} |
 8{3} |
 9{3} |
 10{3} |
 2{4} |
 3{4} |
 4{4} |
 5{4} |
 6{4} |
 7{4} |
2{5} |
 3{5} |
 4{5} |
 5{5} |
 6{5} |
2{5/2} |
 3{5/2} |
 4{5/2} |
 5{5/2} |
 6{5/2} |
 2{6} |
3{6} |
 4{6} |
 5{6} | |
2{7} |
 3{7} |
 4{7} |
2{7/2} |
 3{7/2} |
 4{7/2} |
2{7/3} |
 3{7/3} |
 4{7/3} |
 2{8} |
 3{8} |
 2{8/3} |
 3{8/3} | ||
2{9} |
 3{9} |
2{9/2} |
 3{9/2} |
2{9/4} |
 3{9/4} |
 2{10} |
 3{10} |
 2{10/3} |
 3{10/3} | |||||
 2{11} |
 2{11/2} |
 2{11/3} |
 2{11/4} |
 2{11/5} |
 2{12} |
 2{12/5} |
 2{13} |
 2{13/2} |
 2{13/3} |
 2{13/4} |
 2{13/5} |
 2{13/6} | ||
 2{14} |
 2{14/3} |
 2{14/5} |
 2{15} |
 2{15/2} |
 2{15/4} |
 2{15/7} |
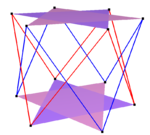
Правильные косые многоугольники также создают соединения, видимые на краях призматического соединения антипризм , например:
| Сложный перекос квадратов |
Сложный перекос шестиугольников |
Сложный перекос десятиугольников | |
| Два {2}#{ } | Три {2}#{ } | Два {3}#{ } | Два {5/3}#{ } |

|

|
|

|
Трехмерные соединения
[ редактировать ] этого раздела Фактическая точность оспаривается . ( январь 2024 г. ) |
Составной правильный многогранник можно определить как составной элемент, который, как и правильный многогранник, является транзитивным по вершинам , транзитивным по ребрам и транзитивным по граням . Согласно этому определению, существует 5 правильных соединений.
| Симметрия | [4,3], О ч | [5,3] + , я | [5,3], I h | ||
|---|---|---|---|---|---|
| Двойственность | Самодвойственный | Двойные пары | |||
| Изображение | 
|

|

|

|

|
| сферический | 
|

|

|

|

|
| Многогранники | 2 {3,3} | 5 {3,3} | 10 {3,3} | 5 {4,3} | 5 {3,4} |
| Коксетер | {4,3} [2 {3,3} ] {3,4} | {5,3} [5 {3,3} ] {3,5} | 2 {5,3} [10 {3,3} ]2 {3,5} | 2 {5,3} [5 {4,3} ] | [5 {3,4} ]2 {3,5} |
Обозначения Коксетера для регулярных соединений приведены в таблице выше с использованием символов Шлефли . Материал внутри квадратных скобок [ d { p , q } ] обозначает компоненты соединения: d отдельные { p , q }. Материал перед квадратными скобками обозначает расположение вершин соединения: c { m , n } [ d { p , q }] представляет собой соединение d { p , q }, разделяющее вершины { m , n } посчитано c раз. Материал после квадратных скобок обозначает расположение граней соединения: [ d { p , q }] e { s , t } представляет собой соединение d { p , q }, имеющих общие грани { s , t }, посчитанные е раз. Их можно комбинировать: таким образом, c { m , n }[ d { p , q }] e { s , t } представляет собой соединение d { p , q }, разделяющее вершины { m , n }, подсчитанные c раз. и грани { s , t } посчитаны e раз. Эти обозначения можно обобщить на соединения любого количества измерений. [ 1 ]
Евклидовы и гиперболические плоские соединения
[ редактировать ]Существует восемнадцать двухпараметрических семейств правильных составных мозаик евклидовой плоскости. В гиперболической плоскости известны пять однопараметрических семейств и семнадцать изолированных случаев, но полнота этого списка пока не доказана.
Евклидовы и гиперболические составные семейства 2 { p , p } (4 ≤ p ≤ ∞, p целое число) аналогичны сферической звезде-октангуле , 2 {3,3}.
| Самодвойственный | Дуалы | Самодвойственный | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞,∞} |

|

|

|

|
| {{4,4}} или {4,4} или {4,4}[2{4,4}]{4,4} |
[2{6,3}]{3,6} | а{6,3} или {6,3}[2{3,6}] |
{{∞,∞}} или a{∞,∞} или {4,∞}[2{∞,∞}]{∞,4} |
| 3 {6,3} | 3 {3,6} | 3 {∞,∞} | |

|

|

| |
| 2{3,6}[3{6,3}]{6,3} | {3,6}[3{3,6}]2{6,3} |
||
Четырехмерные соединения
[ редактировать ]
|

|
| 75 {4,3,3} | 75 {3,3,4} |
|---|
Коксетер перечисляет 32 правильных соединения правильных 4-многогранников в своей книге «Регулярные многогранники» . [ 2 ] Макмаллен добавляет шесть в своей статье « Новые регулярные соединения 4-многогранников» , в которой он также доказывает, что список теперь полон. [ 3 ] В следующих таблицах верхний индекс (var) указывает на то, что помеченные соединения отличаются от других соединений с такими же символами.
| Сложный | Составляющая | Симметрия | Расположение вершин | Расположение ячеек |
|---|---|---|---|---|
| 120 {3,3,3} | 5-клеточный | [5,3,3], порядок 14400 [ 2 ] | {5,3,3} | {3,3,5} |
| 120 {3,3,3} (наш) | 5-клеточный | заказать 1200 [ 3 ] | {5,3,3} | {3,3,5} |
| 720 {3,3,3} | 5-клеточный | [5,3,3], порядок 14400 [ 3 ] | 6{5,3,3} | 6{3,3,5} |
| 5 {3,4,3} | 24-ячеечный | [5,3,3], порядок 14400 [ 2 ] | {3,3,5} | {5,3,3} |
| Соединение 1 | Соединение 2 | Симметрия | Расположение вершин (1) | Расположение ячеек (1) | Расположение вершин (2) | Расположение ячеек (2) |
|---|---|---|---|---|---|---|
| 3 {3,3,4} [ 4 ] | 3 {4,3,3} | [3,4,3], порядок 1152 [ 2 ] | {3,4,3} | 2{3,4,3} | 2{3,4,3} | {3,4,3} |
| 15 {3,3,4} | 15 {4,3,3} | [5,3,3], порядок 14400 [ 2 ] | {3,3,5} | 2{5,3,3} | 2{3,3,5} | {5,3,3} |
| 75 {3,3,4} | 75 {4,3,3} | [5,3,3], порядок 14400 [ 2 ] | 5{3,3,5} | 10{5,3,3} | 10{3,3,5} | 5{5,3,3} |
| 75 {3,3,4} | 75 {4,3,3} | [5,3,3], порядок 14400 [ 2 ] | {5,3,3} | 2{3,3,5} | 2{5,3,3} | {3,3,5} |
| 75 {3,3,4} | 75 {4,3,3} | заказать 600 [ 3 ] | {5,3,3} | 2{3,3,5} | 2{5,3,3} | {3,3,5} |
| 300 {3,3,4} | 300 {4,3,3} | [5,3,3] + , заказ 7200 [ 2 ] | 4{5,3,3} | 8{3,3,5} | 8{5,3,3} | 4{3,3,5} |
| 600 {3,3,4} | 600 {4,3,3} | [5,3,3], порядок 14400 [ 2 ] | 8{5,3,3} | 16{3,3,5} | 16{5,3,3} | 8{3,3,5} |
| 25 {3,4,3} | 25 {3,4,3} | [5,3,3], порядок 14400 [ 2 ] | {5,3,3} | 5{5,3,3} | 5{3,3,5} | {3,3,5} |
Существует два разных соединения 75 тессерактов: один разделяет вершины 120-ячейки, а другой - общие вершины 600-ячейки. Отсюда сразу следует, что соответствующие дуальные соединения 75 16-клеток также различны.
| Сложный | Симметрия | Расположение вершин | Расположение ячеек |
|---|---|---|---|
| 5 {5,5/2,5} | [5,3,3] + , заказ 7200 [ 2 ] | {5,3,3} | {3,3,5} |
| 10 {5,5/2,5} | [5,3,3], порядок 14400 [ 2 ] | 2{5,3,3} | 2{3,3,5} |
| 5 {5/2,5,5/2} | [5,3,3] + , заказ 7200 [ 2 ] | {5,3,3} | {3,3,5} |
| 10 {5/2,5,5/2} | [5,3,3], порядок 14400 [ 2 ] | 2{5,3,3} | 2{3,3,5} |
| Соединение 1 | Соединение 2 | Симметрия | Расположение вершин (1) | Расположение ячеек (1) | Расположение вершин (2) | Расположение ячеек (2) |
|---|---|---|---|---|---|---|
| 5 {3,5,5/2} | 5 {5/2,5,3} | [5,3,3] + , заказ 7200 [ 2 ] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], порядок 14400 [ 2 ] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3] + , заказ 7200 [ 2 ] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], порядок 14400 [ 2 ] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
| 5 {5/2,3,5} | 5 {5,3,5/2} | [5,3,3] + , заказ 7200 [ 2 ] | {5,3,3} | {3,3,5} | {5,3,3} | {3,3,5} |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], порядок 14400 [ 2 ] | 2{5,3,3} | 2{3,3,5} | 2{5,3,3} | 2{3,3,5} |
Существует также четырнадцать частично правильных соединений, которые являются либо вершинно-транзитивными, либо клеточно-транзитивными, но не тем и другим одновременно. Семь вершинно-транзитивных частично правильных соединений являются двойниками семи клеточно-транзитивных частично регулярных соединений.
| Соединение 1 Вершинно-транзитивный |
Соединение 2 Клеточно-транзитивный |
Симметрия |
|---|---|---|
| 2 16-ячеечных [ 5 ] | 2 тессеракта | [4,3,3], порядок 384 [ 2 ] |
| 25 24-ячеечный (наш) | 25 24-ячеечный (наш) | заказать 600 [ 3 ] |
| 100 24-ячеечный | 100 24-ячеечный | [5,3,3] + , заказ 7200 [ 2 ] |
| 200 24-ячеечный | 200 24-ячеечный | [5,3,3], порядок 14400 [ 2 ] |
| 5 600 ячеек | 5 120-ячеечный | [5,3,3] + , заказ 7200 [ 2 ] |
| 10 600-ячеечных | 10 120-ячеечный | [5,3,3], порядок 14400 [ 2 ] |
| Соединение 1 Вершинно-транзитивный |
Соединение 2 Клеточно-транзитивный |
Симметрия |
|---|---|---|
| 5 {3,3,5/2} | 5 {5/2,3,3} | [5,3,3] + , заказ 7200 [ 2 ] |
| 10 {3,3,5/2} | 10 {5/2,3,3} | [5,3,3], порядок 14400 [ 2 ] |
Хотя и 5-ячеечная, и 24-клеточная являются самодвойственными, их двойственные соединения ( соединение двух 5-клеток и соединение двух 24-клеток ) не считаются правильными, в отличие от соединения двух тетраэдров и различных соединения двойных многоугольников, поскольку они не являются ни вершинно-правильными, ни клеточно-регулярными: они не являются гранями или звездочками какого-либо правильного 4-многогранника. Однако они транзитивны по вершинам, ребрам, граням и ячейкам.
Евклидовы трехмерные соединения
[ редактировать ]Единственные правильные евклидовы составные соты представляют собой бесконечное семейство составных кубических сот , все вершины и грани которых имеют общие вершины и грани с другими кубическими сотами. Это соединение может иметь любое количество кубических сот. Обозначение Кокстера: {4,3,4}[ d {4,3,4}]{4,3,4}.
Пять измерений и высшие соединения
[ редактировать ]Не существует правильных соединений в пяти или шести измерениях. Известны три семимерных соединения (16, 240 или 480 7-симплексов ) и шесть известных восьмимерных соединений (16, 240 или 480 8-кубов или 8-ортоплексов ). Существует также одно соединение из n -симплексов в n -мерном пространстве при условии, что n на единицу меньше степени двойки, а также два соединения (одно из n -кубов и двойственное из n -ортоплексов) в n -мерном пространстве. если n — степень двойки.
Обозначения Кокстера для этих соединений (с использованием α н = {3 п -1 }, б н = {3 п -2 ,4}, γ n = {4,3 п -2 }):
- 7-симплексы: c γ 7 [16 c α 7 ] c β 7 , где c = 1, 15 или 30.
- 8-ортоплексы: c γ 8 [16 c β 8 ]
- 8-кубики: [16 c γ 8 ] c β 8
Общие случаи (где n = 2 к и д = 2 2 к - к - 1 , k = 2, 3, 4, ...):
- Симплексы: γ n −1 [ d α n −1 ]β n −1
- Ортоплексы: γ n [ d β n ]
- Гиперкубы: [ d γ n ]β n
Евклидовы сотовые соединения
[ редактировать ]Известное семейство правильных евклидовых составных сот в пяти или более измерениях представляет собой бесконечное семейство составных гиперкубических сот , все вершины и грани которых имеют общие вершины и грани с другими гиперкубическими сотами. Это соединение может иметь любое количество гиперкубических сот. Обозначение Кокстера: δ n [ d δ n ]δ n , где δ n = {∞}, когда n = 2 и {4,3 п -3 ,4}, когда n ≥ 3.
Ссылки
[ редактировать ]- ^ Коксетер (1973) , с. 48.
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа Коксетер (1973) . Таблица VII, с. 305
- ^ Jump up to: а б с д и МакМаллен (2018) .
- ^ Клитцинг, Ричард. «Однородное сложное звездчатое икоситетрахорон» .
- ^ Клитцинг, Ричард. «Единый составной демидистессеракт» .
Библиография
[ редактировать ]- Коксетер, HSM (1973) [1948]. Правильные многогранники (Третье изд.). Нью-Йорк: Dover Publications. ISBN 0-486-61480-8 . МР 0370327 . OCLC 798003 . См., в частности, Таблицы I и II: Правильные многогранники и соты, стр. 294–296.
- МакМаллен, Питер (2018), «Новые регулярные соединения 4-многогранников», Новые тенденции в интуитивной геометрии , Математические исследования Общества Боляи, том. 27, стр. 307–320, номер документа : 10.1007/978-3-662-57413-3_12 , ISBN. 978-3-662-57412-6 .