Полигональная сетка
Эта статья нуждается в дополнительных цитатах для проверки . ( июнь 2009 г. ) |

В компьютерной 3D-графике и твердотельном моделировании полигональная сетка представляет собой набор вершины , край s и грань s , определяющая форму многогранного объекта. Грани обычно состоят из треугольников ( треугольная сетка ), четырехугольников (квадраты) или других простых выпуклых многоугольников ( n-угольников ), поскольку это упрощает рендеринг , но в более общем случае могут также состоять из вогнутых многоугольников или даже многоугольников с отверстиями .
Исследование полигональных сеток — это большая область компьютерной графики (в частности, 3D-компьютерной графики) и геометрического моделирования . Различные представления полигональных сеток используются для разных приложений и целей. Разнообразие операций, выполняемых над сетками, может включать: Булеву логику ( Конструктивная твердотельная геометрия ), сглаживание , упрощение и многие другие. Также существуют алгоритмы трассировки лучей , обнаружения столкновений и динамики твердого тела с полигональными сетками. Если вместо граней визуализируются края сетки, модель становится каркасной .
Объемные сетки отличаются от полигональных сеток тем, что они явно представляют как поверхность, так и объем конструкции, тогда как полигональные сетки явно представляют только поверхность (объем неявно).
Существует несколько методов генерации сетки , включая алгоритм марширующих кубов . [1]
Элементы
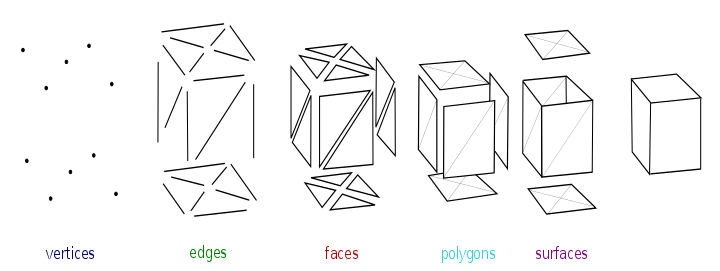
[ редактировать ]Объекты, созданные с помощью полигональных сеток, должны хранить элементы разных типов. К ним относятся вершины, ребра, грани, многоугольники и поверхности. Во многих приложениях сохраняются только вершины, ребра, а также грани или многоугольники. Средство визуализации может поддерживать только трехсторонние грани, поэтому многоугольники должны состоять из многих из них, как показано выше. Однако многие средства визуализации либо поддерживают четырехугольники и многоугольники с более высокими сторонами, либо могут конвертировать многоугольники в треугольники на лету, что делает ненужным хранение сетки в треугольной форме.
Представительства
[ редактировать ]Полигональные сетки могут быть представлены различными способами, используя разные методы для хранения данных вершин, ребер и граней. К ним относятся:
VV«Сетка представляет только вершины, которые указывают на другие вершины. Информация как о ребре, так и о грани неявно присутствует в представлении. Однако простота представления не позволяет выполнять многие эффективные операции над сетками. Каждое из приведенных выше представлений имеет определенные преимущества и недостатки, которые далее обсуждаются Смитом (2006). [2] Выбор структуры данных зависит от приложения, требуемой производительности, размера данных и выполняемых операций. Например, с треугольниками легче иметь дело, чем с обычными многоугольниками, особенно в вычислительной геометрии . Для определенных операций необходим быстрый доступ к топологической информации, такой как ребра или соседние грани; для этого требуются более сложные структуры, такие как представление с крылатым краем. Для аппаратного рендеринга нужны компактные, простые конструкции; таким образом, угловой стол (треугольный веер) обычно включается в API низкоуровневого рендеринга, такие как DirectX и OpenGL .
Вершинно-вершинные сетки
[ редактировать ]
Сетки вершин-вершин представляют объект как набор вершин, соединенных с другими вершинами. Это самое простое представление, но оно не широко используется, поскольку информация о грани и ребре неявна. Таким образом, необходимо пройти по данным, чтобы сформировать список лиц для рендеринга. Кроме того, операции с ребрами и гранями выполнить непросто.
Однако сетки VV выигрывают от небольшого пространства для хранения и эффективного морфинга формы. На рисунке выше показан четырехсторонний прямоугольник, представленный сеткой VV. Каждая вершина индексирует соседние вершины. Последние две вершины, 8 и 9 в верхней и нижней центральной части «цилиндра-коробки», имеют четыре соединенных вершины, а не пять. Общая система должна иметь возможность обрабатывать произвольное количество вершин, связанных с любой заданной вершиной.
Полное описание сетей VV см. в Smith (2006). [2]
Сетки граней-вершин
[ редактировать ]
Сетки граней-вершин представляют объект как набор граней и набор вершин. Это наиболее широко используемое представление сетки, которое обычно принимается современным графическим оборудованием.
Сетки граней-вертексов совершенствуют VV-сетки для моделирования, поскольку позволяют явно искать вершины грани и грани, окружающие вершину. На рисунке выше показан пример «коробка-цилиндр» в виде сетки FV. Вершина v5 выделена, чтобы показать окружающие ее грани. Обратите внимание, что в этом примере каждая грань должна иметь ровно 3 вершины. Однако это не означает, что каждая вершина имеет одинаковое количество окружающих граней.
Для рендеринга список граней обычно передается в графический процессор как набор индексов вершин, а вершины передаются как структуры позиция/цвет/нормаль (на рисунке указана только позиция). Преимущество этого заключается в том, что изменения формы, но не геометрии, можно динамически обновлять, просто повторно отправляя данные вершин без обновления связности граней.
Моделирование требует легкого обхода всех структур. С помощью сеток граней-вертексов легко найти вершины грани. Кроме того, список вершин содержит список граней, связанных с каждой вершиной. В отличие от сеток VV, и грани, и вершины являются явными, поэтому поиск соседних граней и вершин занимает постоянное время. Однако края неявны, поэтому поиск всех граней, окружающих данную грань, все равно необходим. Другие динамические операции, такие как разделение или объединение граней, также затруднены с сетками граней-вершин.
Сетки с крыльями
[ редактировать ]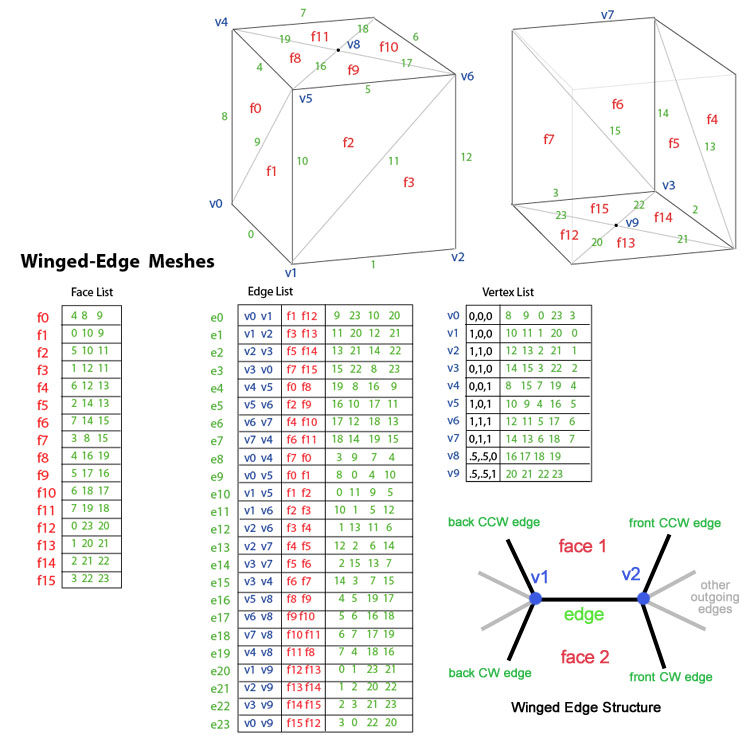
представленные Баумгартом в 1975 году, Сетки с крылатыми краями, явно представляют вершины, грани и края сетки. Это представление широко используется в программах моделирования для обеспечения наибольшей гибкости при динамическом изменении геометрии сетки, поскольку операции разделения и слияния можно выполнять быстро. Их основной недостаток — большие требования к объему памяти и повышенная сложность из-за поддержки множества индексов. Хорошее обсуждение вопросов реализации сеток Winged-edge можно найти в книге Graphics Gems II .
Сети с крыльями решают проблему перемещения от края к краю и обеспечивают упорядоченный набор граней вокруг края. Для любого данного ребра количество исходящих ребер может быть произвольным. Чтобы упростить это, сетки с крылатыми краями предоставляют только четыре, ближайшие по часовой стрелке и против часовой стрелки ребра на каждом конце. Остальные края можно перемещать постепенно. Таким образом, информация для каждого ребра напоминает бабочку, отсюда и сетки с «крылатыми краями». На рисунке выше «коробка-цилиндр» показана в виде сетки с крыльями. Общие данные для ребра состоят из 2 вершин (конечных точек), 2 граней (с каждой стороны) и 4 ребер (крылатого ребра).
Рендеринг сеток с крыльями для графического оборудования требует создания списка индексов лиц. Обычно это делается только при изменении геометрии. Сетки с крыльями идеально подходят для динамической геометрии, такой как поверхности разделения и интерактивное моделирование, поскольку изменения в сетке могут происходить локально. Обход сетки, который может потребоваться для обнаружения столкновений, может быть выполнен эффективно.
Более подробную информацию см. в Baumgart (1975). [3]
Рендеринг динамических сеток
[ редактировать ]Сетки с крыльями — не единственное представление, позволяющее динамически изменять геометрию. Новое представление, которое объединяет сетки с крылатыми краями и сетки с гранями-вершинами, — это динамическая сетка рендеринга , которая явно хранит как вершины грани, так и грани вершины (например, сетки FV), а также грани и вершины грани ( как крылатый край).
Для визуализации динамических сеток требуется немного меньше места для хранения, чем для стандартных сеток с крылатыми краями, и их можно напрямую визуализировать с помощью графического оборудования, поскольку список граней содержит индекс вершин. Кроме того, переход от вершины к грани является явным (постоянное время), как и от грани к вершине. Сетки RD не требуют четырех исходящих ребер, поскольку их можно найти, перемещаясь от края к грани, а затем лицом к соседнему ребру.
Сетки RD выигрывают от особенностей сеток с крылатыми краями, позволяя динамически обновлять геометрию.
см. в Tobler & Maierhofer ( WSCG 2006). Более подробную информацию [4]
Краткое описание представления сетки
[ редактировать ]| Операция | Вершина-вершина | Face-вершина | Крылатый край | Рендеринг динамический | |
|---|---|---|---|---|---|
| V-V | Все вершины вокруг вершины | Явный | V → f1, f2, f3, ... → v1, v2, v3, ... | V → e1, e2, e3, ... → v1, v2, v3, ... | V → e1, e2, e3, ... → v1, v2, v3, ... |
| ЭФ | Все края лица | F(a,b,c) → {a,b}, {b,c}, {a,c} | F → {a,b}, {b,c}, {a,c} | Явный | Явный |
| ВФ | Все вершины грани | F(a,b,c) → {a,b,c} | Явный | F → e1, e2, e3 → a, b, c | Явный |
| ФВ | Все грани вокруг вершины | Поиск пары | Явный | V → e1, e2, e3 → f1, f2, f3, ... | Явный |
| ЕВ | Все ребра вокруг вершины | V → {v,v1}, {v,v2}, {v,v3}, ... | V → f1, f2, f3, ... → v1, v2, v3, ... | Явный | Явный |
| ИП | Обе грани ребра | Сравнить список | Сравнить список | Явный | Явный |
| ВЕ | Обе вершины ребра | E(a,b) → {a,b} | E(a,b) → {a,b} | Явный | Явный |
| Флук | Найти грань с заданными вершинами | F(a,b,c) → {a,b,c} | Установить пересечение v1,v2,v3 | Установить пересечение v1,v2,v3 | Установить пересечение v1,v2,v3 |
| Размер хранилища | V*avg(V,V) | 3F + V*avg(F,V) | 3F + 8E + В*ср(Е,В) | 6F + 4E + В*ср(Е,В) | |
| Пример с 10 вершинами, 16 гранями, 24 ребрами: | |||||
| 10 * 5 = 50 | 3*16 + 10*5 = 98 | 3*16 + 8*24 + 10*5 = 290 | 6*16 + 4*24 + 10*5 = 242 | ||
| Рисунок 6: сводка операций представления сетки. | |||||
В приведенной выше таблице явно указано, что операцию можно выполнить за постоянное время, поскольку данные сохраняются напрямую; сравнение списков указывает, что для выполнения операции необходимо выполнить сравнение списков между двумя списками; а поиск пары указывает, что поиск необходимо выполнить по двум индексам. Обозначение avg(V,V) означает среднее количество вершин, соединенных с данной вершиной; avg(E,V) означает среднее количество ребер, соединенных с данной вершиной, а avg(F,V) — среднее количество граней, соединенных с данной вершиной.
Обозначение «V → f1, f2, f3, ... → v1, v2, v3, ...» описывает, что для выполнения операции требуется обход нескольких элементов. Например, чтобы получить «все вершины вокруг данной вершины V» с помощью сетки граней-вершин, необходимо сначала найти грани вокруг данной вершины V, используя список вершин. Затем по этим граням используйте список граней, чтобы найти вершины вокруг них. Сетки с крылатыми краями явно хранят почти всю информацию, а другие операции всегда сначала обращаются к краю, чтобы получить дополнительную информацию. Сетки вершин-вершин — единственное представление, которое явно хранит соседние вершины данной вершины.
По мере того как представления сетки становятся более сложными (слева направо в сводке), объем явно хранимой информации увеличивается. Это дает более прямой, постоянный доступ к обходу и топологии различных элементов, но за счет увеличения накладных расходов и пространства для правильного поддержания индексов.
На рис. 7 показана информация о подключении для каждого из четырех методов, описанных в этой статье. Существуют и другие представления, такие как полукраевые и угловые таблицы. Все это варианты того, как вершины, грани и ребра индексируют друг друга.
Как правило, сетки граней-вершин используются всякий раз, когда объект должен быть визуализирован на графическом оборудовании, которое не меняет геометрию (связность), но может деформировать или трансформировать форму (положение вершин), например, в реальном времени. рендеринг статических или морфируемых объектов . Динамические сетки с крыльями или рендерингом используются при изменении геометрии, например, в пакетах интерактивного моделирования или для расчета поверхностей разделения. Сетки вершин-вершин идеально подходят для эффективных и сложных изменений геометрии или топологии, если не требуется аппаратный рендеринг.
Другие представления
[ редактировать ]Форматы файлов
[ редактировать ]Существует множество различных форматов файлов для хранения данных полигональной сетки. Каждый формат наиболее эффективен, когда используется по назначению его создателя. Популярные форматы включают .fbx , .dae , .obj и .stl . Таблица еще некоторых из этих форматов представлена ниже:
| Суффикс файла | Имя формата | Организация(и) | Программа(ы) | Описание |
|---|---|---|---|---|
| .сырой | Необработанная сетка | Неизвестный | Различный | Открытый формат только ASCII. Каждая строка содержит 3 вершины, разделенные пробелами, образующие треугольник, например: X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3. |
| .смешивать | Формат файла блендера | Фонд Блендера | Blender 3D | Открытый исходный код, только двоичный формат |
| .fbx | Формат Autodesk FBX | Автодеск | Различный | Собственный. Существуют двоичные спецификации и спецификации ASCII. |
| .3ds | Файл 3ds Max | Автодеск | 3дс Макс | Распространенный, но устаревший формат с жесткими 16-битными ограничениями на количество вершин и граней. Не стандартизирован и не документирован, но раньше был «стандартом де-факто» для обмена данными. |
| .дней | Биржа цифровых активов (COLLADA) | Sony Computer Entertainment , Khronos Group | Н/Д | означает « COLLA borative Design Activity Аббревиатура ». Универсальный формат, предназначенный для предотвращения несовместимости. |
| .с | Файл MicroStation | Бентли Системс | Микростанция | Существует два формата файлов dgn: предварительная версия 8 и версия 8 (V8). |
| .3дм | Носорог Файл | Роберт МакНил и партнеры | Носорог 3D | |
| .dxf , .dwg | Формат обмена чертежами | Автодеск | Автокад | |
| .obj | Волновой фронт OBJ | Волновые Технологии | Различный | Формат ASCII, описывающий трехмерную геометрию. Вершины всех граней упорядочены против часовой стрелки, что делает нормали граней неявными. Гладкие нормали задаются для каждой вершины. |
| .ply | Формат файла многоугольника | Стэнфордский университет | Различный | Двоичный и ASCII |
| .pmd | Данные Polygon Movie Maker | Ю Хигучи | МикуМикуDance | Собственный двоичный формат файла для хранения геометрии модели гуманоида с информацией о оснастке, материале и физике. |
| .stl | стереолитографии Формат | 3D-системы | Много | Двоичный формат и формат ASCII, изначально разработанный для использования в ЧПУ . |
| .amf | Формат файла аддитивного производства | АСТМ Интернешнл | Н/Д | Подобен формату STL, но с добавленной поддержкой собственных цветов, материалов и созвездий. |
| .wrl | Язык моделирования виртуальной реальности | Консорциум Web3D | Веб-браузеры | Стандарт ИСО 14772-1:1997. |
| .Сентябрь | VRML сжатый | Консорциум Web3D | Веб-браузеры | |
| .x3d, .x3db, .x3dv | Расширяемое 3D | Консорциум Web3D | Веб-браузеры | Основанный на XML, с открытым исходным кодом, бесплатный, расширяемый и совместимый; также поддерживает информацию о цвете, текстуре и сцене. Стандарт ИСО 19775/19776/19777 |
| .x3dz, .x3dbz, .x3dvz | X3D-сжатый двоичный файл | Консорциум Web3D | Веб-браузеры | |
| .c4d | Файл Cinema 4D | Максон | КИНО 4D | |
| .lwo | Файл объекта LightWave 3D | НьюТек | ЛайтВейв 3D | |
| .smb | SCOREC апф | ОЦЕНКА RPI | ПУМИ | Параллельно-адаптивные неструктурированные 3D-сетки с открытым исходным кодом для рабочих процессов моделирования на основе PDE. |
| .мш | Гмш сетка | Разработчики ГМш | Проект ГМш | Открытый исходный код, предоставляющий описание сетки ASCII для линейных и полиномиально интерполированных элементов в 1–3 измерениях. |
| .сетка | ОГРЕ XML | Команда разработчиков OGRE | ОГРЕ, чистоосновный | Открытый исходный код. Доступны двоичный (.mesh) и ASCII (.mesh.xml) форматы. Включает данные для вершинной анимации и целевой анимации Morph (blendshape). Данные скелетной анимации в отдельном файле (.skeleton). |
| .дорога | Тетраэдрическая сетка Vega FEM | Ерней Барбич | Вега ПЯТЬ | Открытый исходный код. Сохраняет тетраэдральную сетку и свойства ее материала для моделирования FEM. Доступны форматы ASCII (.veg) и двоичные (.vegb). |
| . z3d | Z3d | Oleg Melashenko | Zanoza Modeler | - |
| .vtk | Сетка ВТК | ВТК , Комплект поставки | ВТК , Паравью | Открытый формат ASCII или двоичный формат, содержащий множество различных полей данных, включая данные точек, данные ячеек и данные полей. |
| .l4d | LAI4D рисунок | Лаборатория искусственного интеллекта для дизайна | ЛАИ4Д | Формат данных ASCII, описывающий иерархическое дерево объектов. |
См. также
[ редактировать ]- Граничное представление
- оператор Эйлера
- Гиперграф
- Многообразие (сетка может быть многообразной или не многообразной)
- Подразделение сетки (метод добавления деталей к полигональной сетке)
- Полигональное моделирование
- Полигонизатор
- Симплекс
- Т-образный шлиец
- Триангуляция (геометрия)
- Каркасная модель
Ссылки
[ редактировать ]- ^ Лоренсен, Уильям Э.; Клайн, Харви Э. (1 августа 1987 г.). «Марширующие кубы: алгоритм построения трехмерной поверхности высокого разрешения». ACM SIGGRAPH Компьютерная графика . 21 (4): 163–169. CiteSeerX 10.1.1.545.613 . дои : 10.1145/37402.37422 .
- ^ Перейти обратно: а б Колин Смит, О вершинно-вершинных сетках и их использовании в геометрическом и биологическом моделировании , ( PDF )
- ^ Брюс Баумгарт, Представление многогранника с крылатыми краями для компьютерного зрения. Национальная компьютерная конференция, май 1975 г. «Использование многогранников в компьютерном зрении» . baumgart.org . Май 1975 г. Архивировано из оригинала 29 августа 2005 г. Проверено 29 августа 2005 г.
- ^ Тоблер и Майерхофер, Сетчатая структура данных для рендеринга и подразделения. 2006 год . ( PDF )