Внешний функтор
В математике функторы Ext являются производными функторами функтора Hom . Наряду с функтором Tor , Ext является одним из основных понятий гомологической алгебры , в которой идеи алгебраической топологии используются для определения инвариантов алгебраических структур. Когомологии групп , алгебр Ли и ассоциативных алгебр могут быть определены в терминах Ext. Название происходит от того, что первая группа Ext Ext 1 классифицирует расширения одного модуля по другому.
В частном случае абелевых групп Ext был введен Рейнхольдом Баером (1934). Он был назван Сэмюэлем Эйленбергом и Сондерсом Маклейном (1942) и применен к топологии ( теорема об универсальных коэффициентах для когомологий ). Для модулей над любым кольцом Ext был определен Анри Картаном и Эйленбергом в их книге 1956 года «Гомологическая алгебра» . [1]
Определение
[ редактировать ]Пусть R — кольцо и R -Mod — модулей над R. категория (Можно понимать, что это означает либо левые R -модули, либо правые R -модули.) Для фиксированного R -модуля A пусть T ( B ) = Hom R ( A , B ) для B в R -Mod. (Здесь Hom R ( A , B ) — абелева группа R -линейных отображений из A в B ; это R если R коммутативен -модуль , .) Это точный слева функтор из R -Mod в категорию абелевых группы Ab, и поэтому он имеет правые производные функторы R я Т. Группы Ext — это абелевы группы, определенные формулой
для целого числа i . По определению это означает: возьмите любую инъективную резольвенту
удалите термин B и сформируйте комплекс коцепи :
Для каждого целого числа i Ext я
R ( A , B ) — когомологии этого комплекса в позиции i . Это ноль для i отрицательного. Например, Экст. 0
R ( A , B ) — ядро отображения Hom R ( A , I 0 ) → Hom R ( A , I 1 ), который изоморфен Hom R ( A , B ).
Альтернативное определение использует функтор G ( A )=Hom R ( A , B ) для фиксированного R -модуля B . Это контравариантный функтор, который можно рассматривать как точный слева функтор из противоположной категории ( R -Mod ). на Абу. Группы Ext определяются как правые производные функторы R я Г :
То есть выберите любое проективное разрешение
удалите термин A и сформируйте комплекс коцепи:
Затем доб. я
R ( A , B ) — когомологии этого комплекса в позиции i .
Можно задаться вопросом, почему выбор резолюции до сих пор остается неясным. Фактически Картан и Эйленберг показали, что эти конструкции не зависят от выбора проективной или инъективной резольвенты и что обе конструкции дают одни и те же Ext-группы. [2] Более того, для фиксированного кольца R Ext является функтором от каждой переменной (контравариантным в A , ковариантным в B ).
Для коммутативного кольца R и R -модулей A и B Ext я
R ( A , B ) является R -модулем (поскольку в данном случае Hom R ( A , B ) является R -модулем). Для некоммутативного кольца R Ext я
R ( A , B ) вообще говоря, является лишь абелевой группой. Если R — алгебра над кольцом S (что, в частности, означает, что S коммутативно), то Ext я
R ( A , B ) является по крайней мере S -модулем.
Свойства расширения
[ редактировать ]Вот некоторые основные свойства и вычисления групп Ext. [3]
- доб. 0
R ( A , B ) ≅ Hom R ( A , B ) для любых R -модулей A и B .
- доб. я
R ( A , B ) = 0 для всех i > 0, если - модуль A проективен R (например, свободен ) или B инъективен если .
- Обратные утверждения также справедливы:
- Если доб. 1
R ( A , B ) = 0 для всех B , то A проективен (и, следовательно, Ext я
R ( A , B ) = 0 для всех i > 0). - Если доб. 1
R ( A , B ) = 0 для всех A , то B инъективен (и, следовательно, Ext я
R ( A , B ) = 0 для всех i > 0).
- Если доб. 1
- для всех i ≥ 2 и всех абелевых A и B. групп [4]
- Если R — коммутативное кольцо и u в R не является делителем нуля , то
- для любого R -модуля B . Здесь B [ u ] обозначает u -периодическую подгруппу группы B , { x ∈ B : ux = 0}. Приняв R за кольцо целых чисел, это вычисление можно использовать для вычисления для любой конечно порожденной абелевой группы A .
- Обобщая предыдущий пример, можно вычислить группы Ext, когда первый модуль является фактором коммутативного кольца по любой регулярной последовательности , используя комплекс Кошуля . [5] Например, если R — кольцо многочленов k [ x 1 ,..., x n ] над полем k , то Ext *
R ( k , k ) — внешняя алгебра S над k на n образующих в Ext 1 . Более того, доб. *
S ( k , k ) — кольцо полиномов R ; это пример двойственности Кошуля .
- По общим свойствам производных функторов существуют две основные точные последовательности для Ext. [6] Во-первых, короткая точная последовательность 0 → K → L → M → 0 R -модулей индуцирует длинную точную последовательность вида
- для любого R модуля A. - Кроме того, короткая точная последовательность 0 → K → L → M → 0 индуцирует длинную точную последовательность вида
- для любого R -модуля B .
- Ext преобразует прямые суммы (возможно, бесконечные) в первую переменную и произведения во второй переменной в произведения. [7] То есть:
- Пусть A конечно порожденный модуль над коммутативным нетеровым кольцом R. — Тогда Ext коммутирует с локализацией в том смысле, что для любого мультипликативно замкнутого множества S в R , каждого R -модуля B и каждого целого i числа [8]
Расширения и расширения
[ редактировать ]Эквивалентность расширений
[ редактировать ]Группы Ext получили свое название от расширения модулей. данных R -модулей A и B расширение A Для с помощью B представляет собой короткую точную последовательность R -модулей.
Два расширения
называются эквивалентными (как расширение A посредством B ), если существует коммутативная диаграмма :
Обратите внимание, что из леммы о пяти следует, что средняя стрелка является изоморфизмом. Расширение A посредством B называется расщепленным , если оно эквивалентно тривиальному расширению
существует взаимно однозначное соответствие. Между классами эквивалентности расширений A посредством B и элементами Ext 1
Р ( А , Б ). [9] Тривиальное расширение соответствует нулевому элементу Ext 1
Р ( А , Б ).
Сумма Бэра расширений
[ редактировать ]Сумма Бэра является явным описанием структуры абелевой группы на Ext 1
R ( A , B ), рассматриваемый как множество классов эквивалентности расширений A с помощью B . [10] А именно, учитывая два расширения
и
сначала откат сформируйте ,
Затем сформируем фактор-модуль
Сумма Бэра E и E ' является расширением
где первая карта и второй .
С точностью до эквивалентности расширений сумма Бэра коммутативна и имеет в качестве единичного элемента тривиальное расширение. Негатив расширения 0 → B → E → A → 0 — это расширение, включающее тот же модуль E гомоморфизма B → E , но с заменой на его негатив.
Построение Ext в абелевых категориях
[ редактировать ]Нобуо Йонеда определил абелевы группы Ext н
C ( A , B ) для объектов A и B в любой абелевой категории C ; это согласуется с определением в терминах резольвент, если C имеет достаточно проективов или достаточно инъективов . Во-первых, доб. 0
C ( А , B ) знак равно Hom C ( А , B ). Далее, доб. 1
C ( A , B ) — множество классов эквивалентности расширений A с помощью B , образующих абелеву группу относительно суммы Бэра. Наконец, высшие группы Ext Ext н
C ( A , B ) определяются как классы эквивалентности n-расширений , которые являются точными последовательностями
под отношением эквивалентности, порожденным отношением, которое идентифицирует два расширения
если есть карты для всех m из {1, 2, ..., n } так, чтобы каждый полученный квадрат коммутировал то есть, если есть карта цепочки что является тождеством на A и B .
Сумма Бэра двух n -расширений, как указано выше, формируется, если быть откатом и над A и быть вытеснением и под Б. [11] Тогда сумма Бэра расширений равна
Производная категория и продукт Yoneda
[ редактировать ]Важным моментом является то, что группы Ext в абелевой категории C можно рассматривать как множества морфизмов в категории, ассоциированной с C , производной категории D ( C ). [12] Объекты производной категории — это комплексы объектов C. в В частности, у человека есть
где объект C рассматривается как комплекс, сконцентрированный в нулевой степени, а [ i ] означает сдвиг комплекса на i шагов влево. Из этой интерпретации получается билинейное отображение , иногда называемое произведением Йонеды :
что представляет собой просто композицию морфизмов производной категории.
Продукт Yoneda можно описать и более элементарно. Для i = j = 0 продуктом является композиция карт в C. категории В общем, продукт можно определить путем объединения двух расширений Yoneda.
В качестве альтернативы продукт Yoneda можно определить с точки зрения разрешения. (Это близко к определению производной категории.) Например, пусть R — кольцо с R- модулями A , B , C и пусть , Q и T — проективные резольвенты A , B , C. P Затем доб. я
R ( A , B ) можно отождествить с группой цепных гомотопических классов цепных отображений P → Q [ i ]. Продукт Йонеды задается путем составления цепных карт:
В любой из этих интерпретаций произведение Йонеды ассоциативно. Как результат, является градуированным кольцом для любого R - A. модуля Например, это дает кольцевую структуру групповых когомологий. поскольку это можно рассматривать как . Также по ассоциативности произведения Йонеды: для любых R -модулей A и B , это модуль над .
Важные особые случаи
[ редактировать ]- Групповые когомологии определяются формулой , где G группа, M — представление G — над целыми числами и является кольцом G . групповым
- Когомологии алгебры Ли определяются формулой , где — алгебра Ли над коммутативным кольцом k , M — -модуль и — универсальная обертывающая алгебра .
- Для пространства X топологического пучковые когомологии можно определить как Здесь Ext берется в абелевой категории пучков абелевых групп на X , а представляет собой пучок локально постоянных -значные функции.
- Для коммутативного нётерова локального кольца R с полем k вычетов — универсальная обертывающая алгебра градуированной алгебры Ли π*( R ) над k , известная как гомотопическая алгебра Ли R . (Точнее, когда k имеет характеристику 2, π*( R ) следует рассматривать как «скорректированную алгебру Ли». [13] ) Существует естественный гомоморфизм градуированных алгебр Ли из когомологий Андре–Квиллена D *( k / R , k ) в π*( R ), который является изоморфизмом, если k имеет нулевую характеристику. [14]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Вейбель (1999); Картан и Эйленберг (1956), раздел VI.1.
- ^ Weibel (1994), разделы 2.4 и 2.5 и теорема 2.7.6.
- ^ Вайбель (1994), главы 2 и 3.
- ^ Вейбейл (1994), Лемма 3.3.1.
- ^ Вайбель (1994), раздел 4.5.
- ^ Вейбель (1994), Определение 2.1.1.
- ^ Вейбель (1994), Предложение 3.3.4.
- ^ Вейбель (1994), Предложение 3.3.10.
- ^ Вейбель (1994), Теорема 3.4.3.
- ^ Вейбель (1994), Следствие 3.4.5.
- ^ Вайбель (1994), Висты 3.4.6. Некоторые незначительные исправления содержатся в опечатках .
- ^ Weibel (1994), разделы 10.4 и 10.7; Гельфанд и Манин (2003), Глава III.
- ^ Сьёдин (1980), обозначение 14.
- ^ Аврамов (2010), раздел 10.2.
Ссылки
[ редактировать ]- Аврамов, Лучезар (2010), «Бесконечные свободные резолюции», Шесть лекций по коммутативной алгебре , Биркхойзер , стр. 1–108, doi : 10.1007/978-3-0346-0329-4_1 , ISBN 978-3-7643-5951-5 , МР 2641236
- Баер, Рейнхольд (1934), «Расширение групп и их изоморфизмы», Mathematical Journal , 38 (1): 375–416, doi : 10.1007/BF01170643 , Zbl 0009.01101
- Картан, Анри ; Эйленберг, Сэмюэл (1999) [1956], Гомологическая алгебра , Принстон: Princeton University Press , ISBN 0-691-04991-2 , МР 0077480
- Эйленберг, Сэмюэл ; Маклейн, Сондерс (1942), «Расширения групп и гомологии», Annals of Mathematics , 43 (4): 757–931, doi : 10.2307/1968966 , JSTOR 1968966 , MR 0007108
- Гельфанд, Сергей И.; Манин, Юрий Иванович (2003), Методы гомологической алгебры , Берлин, Нью-Йорк: Springer-Verlag , doi : 10.1007/978-3-662-12492-5 , ISBN 978-3-540-43583-9 , МР 1950475
- Сьёдин, Гуннар (1980), «Алгебры Хопфа и дифференцирования», Journal of Algebra , 64 : 218–229, doi : 10.1016/0021-8693(80)90143-X , MR 0575792
- Вейбель, Чарльз А. (1994). Введение в гомологическую алгебру . Кембриджские исследования по высшей математике. Том. 38. Издательство Кембриджского университета. ISBN 978-0-521-55987-4 . МР 1269324 . OCLC 36131259 .
- Вейбель, Чарльз А. (1999), «История гомологической алгебры» (PDF) , История топологии , Амстердам: Северная Голландия, стр. 797–836, ISBN 9780444823755 , МР 1721123







![{\displaystyle \operatorname {Ext} _{R}^{i}(R/(u),B)\cong {\begin{cases}B[u]&i=0\\B/uB&i=1\\0& {\text{иначе,}}\end{случаи}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29b19b92e3188770f876e89fe5d69f61f2bb030)









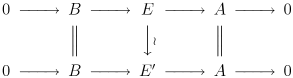

![{\displaystyle 0\to B{\xrightarrow[{f}]{}}E {\xrightarrow[{g}]{}}A\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99b91ef9769c22705bb158052b57276636e7906c)
![{\displaystyle 0\to B{\xrightarrow[{f'}]{}}E'{\xrightarrow[{g'}]{}}A\to 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c3b1f07bd8dcc1d933bb0a1b72b397a6e885e9)




![{\displaystyle b\mapsto [(f(b),0)]=[(0,f'(b))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee75b87481bf9de19754e30ff4b98f9e3a93c53f)













![{\displaystyle \operatorname {Ext} _ {\mathbf {C} }^{i}(A,B)=\operatorname {Hom} _{D({\mathbf {C} })}(A,B[i ]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4f0a89006dc8d51c99160bf062be7b92891c2f)

![{\displaystyle P\to Q[i]\to T[i+j].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1db5574c44feacd2e3448b888bb92c98bb8c17)


![{\displaystyle \operatorname {Ext} _ {\mathbb {Z} [G]}^{*}(\mathbb {Z},\mathbb {Z})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caa2d03e117e399c9fc5a96b1e4383be50277a2b)

![{\displaystyle H^{*}(G,M)=\operatorname {Ext} _ {\mathbb {Z} [G]}^{*}(\mathbb {Z},M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ea5c28b67c0bc2f3dea33b55aa97d33977f830)
![{\displaystyle \mathbb {Z} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40260c366fc309a5872899d2ea34cf094855857)






