Функтор
В математике , особенно в теории категорий , функтор — это отображение между категориями . Функторы были впервые рассмотрены в алгебраической топологии , где алгебраические объекты (такие как фундаментальная группа ) связаны с топологическими пространствами , а карты между этими алгебраическими объектами связаны с непрерывными отображениями между пространствами. В настоящее время функторы используются в современной математике для связи различных категорий. Таким образом, функторы важны во всех областях математики, к которым теория категорий применяется .
Слова категория и функтор были заимствованы математиками у философов Аристотеля и Рудольфа Карнапа соответственно. [1] Последний использовал функтор в лингвистическом контексте; [2] см . функциональное слово .
Определение [ править ]
Эта статья может быть слишком технической для понимания большинства читателей . ( Ноябрь 2023 г. ) |

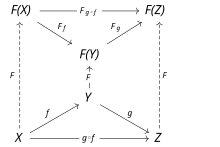
Пусть C и D — категории . Функтор — F из C в D это отображение, которое [3]
- связывает каждый объект в C к объекту в Д ,
- связывает каждый морфизм в C к морфизму в D такие, что выполняются следующие два условия:
- для каждого объекта в С ,
- для всех морфизмов и в С.
То есть функторы должны сохранять тождественные морфизмы и композицию морфизмов.
Ковариантность и контравариантность [ править ]
В математике существует множество конструкций, которые были бы функторами, если бы не тот факт, что они «переворачивают морфизмы» и «обратят композицию». Затем мы определяем контравариантный функтор F из C в D как отображение, которое
- связывает каждый объект в C с объектом в Д ,
- связывает каждый морфизм в C с морфизмом в D такие, что выполняются следующие два условия:
- для каждого объекта в С ,
- для всех морфизмов и в С.
Обратите внимание, что контравариантные функторы меняют направление композиции.
Обыкновенные функторы также называются ковариантными , чтобы отличить их от контравариантных. Обратите внимание, что контравариантный функтор можно также определить как ковариантный функтор в противоположной категории. . [4] Некоторые авторы предпочитают записывать все выражения ковариантно. То есть вместо того, чтобы сказать является контравариантным функтором, они просто пишут (или иногда ) и назовем его функтором.
Контравариантные функторы также иногда называют кофункторами . [5]
Существует соглашение, которое относится к «векторам», т. е. векторным полям , элементам пространства сечений. касательного расслоения — как «контравариантным» и «ковекторам» — т. е. 1-формам , элементам пространства сечений котангенсного расслоения - как «ковариантный». Эта терминология возникла в физике, и ее обоснование связано с положением индексов («наверху» и «внизу») в таких выражениях , как для или для В этом формализме замечено, что символ преобразования координат (представляющий матрицу ) действует на «ковекторные координаты» «так же», как и на базисные векторы: — тогда как на «векторные координаты» он действует «наоборот» (но «так же», как и на базисные ковекторы: ). Эта терминология противоречит той, которая используется в теории категорий, поскольку именно ковекторы имеют откат в целом и, таким образом, являются контравариантными , тогда как векторы в целом являются ковариантными, поскольку их можно сдвигать вперед . См. также Ковариантность и контравариантность векторов .
Противоположная функция [ править ]
Каждый функтор индуцирует противоположный функтор , где и являются , противоположными категориями и . [6] По определению, отображает объекты и морфизмы точно так же, как и . С не совпадает с как категория, и аналогично для , отличается от . Например, при составлении с , следует использовать либо или . Обратите внимание, что, следуя свойству противоположной категории , .
Бифункторы и мультифункторы [ править ]
Бифунктор ) — (также известный как бинарный функтор это функтор, областью определения которого является категория произведения . Например, функтор Hom имеет тип C на × C → Установить . Его можно рассматривать как функтор с двумя аргументами. Функтор Hom является естественным примером; он контрвариантен в одном аргументе и ковариантен в другом.
Мультифунктор — это обобщение концепции функтора на n переменных. Так, например, бифунктор — это мультифунктор с n = 2 .
Свойства [ править ]
функтора Двумя важными следствиями аксиом являются:
- F преобразует каждую коммутативную диаграмму в C в коммутативную диаграмму в D ;
- если f — изоморфизм в C , то F ( f изоморфизм в D. ) —
Можно составить функторы, т. е. если F — функтор из A в B , а G — функтор из B в C, можно сформировать составной функтор G ∘ F из A в C. то Композиция функторов ассоциативна там, где она определена. Тождественность композиции функторов есть тождественный функтор. Это показывает, что функторы можно рассматривать как морфизмы в категориях категорий, например в категории малых категорий .
Небольшая категория с одним объектом — это то же самое, что моноид : морфизмы категории с одним объектом можно рассматривать как элементы моноида, а композицию в категории можно рассматривать как операцию моноида. Функторы между однообъектными категориями соответствуют моноидным гомоморфизмам . Таким образом, в некотором смысле функторы между произвольными категориями являются своего рода обобщением моноидных гомоморфизмов на категории с более чем одним объектом.
Примеры [ править ]
- Диаграмма
- Для категорий C и J диаграмма типа J в C является ковариантным функтором .
- (Теоретическая категория) предпучок
- Для категорий C и J -предпучок J на C является контравариантным функтором. . В особом случае, когда J — это , категория множеств и функций, D называется предпучком на C. Set
- Предпучки (в топологическом пространстве)
- Если X — топологическое пространство , то открытые множества в X образуют частично упорядоченное множество Open( X ) при включении. Как и любое частично упорядоченное множество, Open( X ) образует небольшую категорию, добавляя одну стрелку U → V тогда и только тогда, когда . Контравариантные функторы на Open( X ) называются предпучками на X . Например, присваивая каждому открытому множеству U ассоциативную алгебру вещественнозначных непрерывных функций на U , можно получить предпучок алгебр X. на
- Они постоянно работают
- Функтор C → D , который отображает каждый объект C в фиксированный объект X в D и каждый морфизм в C в тождественный морфизм на X . Такой функтор называется константой или функтором выбора .
- Эндофунктор
- Функтор, сопоставляющий категорию с той же самой категорией; например, полиномиальный функтор .
- Функтор тождества
- В категории C , записанной 1 C или id C , отображает объект в себя и морфизм в себя. Тождественный функтор является эндофунктором.
- Диагональный функтор
- Диагональный функтор определяется как функтор из D в категорию функторов D С который отправляет каждый объект в D постоянному функтору этого объекта.
- Предельный функтор
- с фиксированным индексом Для категории J , если каждый функтор J → C имеет предел (например, если C полно), то предельный функтор C Дж → C присваивает каждому функтору свой предел. Существование этого функтора можно доказать, осознав, что он является правосопряженным к диагональному функтору , и применив теорему Фрейда о сопряженном функторе . Для этого требуется подходящая версия выбранной аксиомы . Аналогичные замечания применимы и к функтору копредела (который присваивает каждому функтору его копредел и является ковариантным).
- Функтор степенных наборов
- Функтор набора мощности P : Set → Set отображает каждый набор на его набор мощности и каждую функцию. на карту, которая отправляет своему образу . Можно также рассмотреть контравариантный функтор набора мощности, который отправляет на карту, которая отправляет к своему обратному образу Например, если затем . Предполагать и . Затем это функция, которая отправляет любое подмножество из своему образу , что в данном случае означает , где обозначает отображение под , так что это также можно записать как . Для остальных значений Обратите внимание, что следовательно, порождает тривиальную топологию на . Также обратите внимание, что хотя функция в этом примере сопоставлено с набором мощности , это не обязательно должно быть так в целом.
- Двойное векторное пространство
- Отображение, которое ставит в соответствие каждому векторному пространству свое двойственное пространство и каждому линейному отображению свое двойственное или транспонированное пространство, является контравариантным функтором из категории всех векторных пространств над фиксированным полем в себя.
- Фундаментальная группа
- Рассмотрим категорию точечных топологических пространств , т.е. топологических пространств с выделенными точками. Объекты представляют собой пары X , x0 ) ( , где X — топологическое пространство, а — точка в X. x0 Морфизм из ( X , x 0 ) в ( Y , y 0 ) задается непрерывным отображением f : X → Y с f ( x 0 ) = y 0 . Для каждого топологического пространства X точкой x0 с отмеченной можно определить группу, в точке , x0 обозначаемую π1 основанную ( X , x0 фундаментальную ) . Это группа гомотопических x0 классов петель, основанных в точке с , групповой операцией конкатенации. Если f : X → Y — морфизм точечных пространств , то каждая петля в X с базовой точкой x 0 может быть составлена с f, чтобы получить петлю в Y с базовой точкой y 0 . Эта операция совместима с отношением гомотопической эквивалентности и композицией петель, и мы получаем групповой гомоморфизм из π( X , x 0 ) в π( Y , y 0 ) . Таким образом, мы получаем функтор из категории точечных топологических пространств в категорию групп . В категории топологических пространств (без выделенной точки) рассматриваются гомотопические классы общих кривых, но они не могут быть составлены, если не имеют общей конечной точки. имеется фундаментальный группоид , и эта конструкция является функториальной. Таким образом, вместо фундаментальной группы
- Алгебра непрерывных функций
- Контравариантный функтор из категории топологических пространств (с непрерывными отображениями в качестве морфизмов) в категорию вещественных ассоциативных алгебр задается путем присвоения каждому топологическому пространству X алгебры C( X ) всех вещественнозначных непрерывных функций на этом пространстве. Каждое непрерывное отображение f : X → Y индуцирует гомоморфизм алгебр C( f ) : C( Y ) → C( X ) по правилу C( f )( φ ) = φ ∘ f для каждого φ в C( Y ).
- Касательные и котангенсные расслоения
- Отображение, которое переводит каждое дифференцируемое многообразие в его касательное расслоение и каждое гладкое отображение в его производную, является ковариантным функтором из категории дифференцируемых многообразий в категорию векторных расслоений . Выполнение этих конструкций поточечно дает касательное пространство , ковариантный функтор из категории заостренных дифференцируемых многообразий в категорию вещественных векторных пространств. Точно так же кокасательное пространство является контравариантным функтором, по сути являющимся композицией касательного пространства с двойственным пространством , указанным выше.
- Групповые действия/представления
- Каждую группу G можно рассматривать как категорию с единственным объектом, морфизмы которого являются элементами G . функтор из G в Set Тогда представляет собой не что иное, как групповое действие G G на конкретном множестве, т. е. -множестве . функтор из в категорию векторных пространств Vect K является линейным представлением G. Аналогично , G В общем, функтор G → C можно рассматривать как «действие» G на объект в категории C . Если C — группа, то это действие является гомоморфизмом группы.
- Алгебры Ли
- Сопоставляя каждой вещественной (комплексной) группе Ли ее вещественную (комплексную) алгебру Ли, мы определяем функтор.
- Тензорные продукты
- Если C обозначает категорию векторных пространств над фиксированным полем с линейными отображениями в качестве морфизмов, то тензорное произведение определяет функтор C × C → C , ковариантный по обоим аргументам. [7]
- Забывчивые функторы
- Функтор U : Grp → Set , который отображает группу в ее основной набор, а гомоморфизм группы в ее основную функцию множеств, является функтором. [8] Подобные функторы, которые «забывают» некоторую структуру, называются забывчивыми функторами . Другим примером является функтор Rng → Ab , который отображает кольцо в лежащую в его основе аддитивную абелеву группу . Морфизмы в Rng ( гомоморфизмы колец ) становятся морфизмами в Ab (гомоморфизмы абелевых групп).
- Свободные функторы
- В противоположном направлении от забывчивых функторов действуют свободные функторы. Свободный функтор F : Set → Grp отправляет каждое множество X в свободную группу порожденную X. , Функции отображаются в групповые гомоморфизмы между свободными группами. Для многих категорий существуют свободные конструкции, основанные на структурированных множествах. Посмотреть свободный объект .
- Группы гомоморфизмов
- Каждой паре A , B абелевых групп можно сопоставить абелеву группу Hom( A , B состоящую из всех гомоморфизмов групп из A в B. ) , Это функтор, контравариантный по первому и ковариантный по второму аргументу, т. е. это функтор Ab на × Ab → Ab (где Ab обозначает категорию абелевых групп с групповыми гомоморфизмами). Если f : A 1 → A 2 и g : B 1 → B 2 являются морфизмами в Ab , то групповой гомоморфизм Hom( f , g ) : Hom( A 2 , B 1 ) → Hom( A 1 , B 2 ) есть ↦ φ г ∘ φ ∘ ж . См. функтор Hom .
- Представимые функторы
- Мы можем обобщить предыдущий пример на любую C. категорию Каждой паре X , Y объектов в C можно сопоставить множество Hom( X , Y ) морфизмов X в Y. из Это определяет функтор для Set , который контравариантен по первому аргументу и ковариантен по второму, т. е. это функтор C на × C → Установить . Если f : X 1 → X 2 и g : Y 1 → Y 2 являются морфизмами в C , то отображение Hom( f , g ) : Hom( X 2 , Y 1 ) → Hom( X 1 , Y 2 ) задано ↦ φ г ∘ φ ∘ ж . Подобные функторы называются представимыми функторами . Во многих случаях важной целью является определение того, представим ли данный функтор.
с другими категориальными Связь понятиями
Пусть C и D — категории. Совокупность всех функторов от C до D образует объекты категории: категория функторов . Морфизмы этой категории представляют собой естественные преобразования между функторами.
Функторы часто определяются универсальными свойствами ; примерами являются тензорное произведение , прямая сумма и прямое произведение групп или векторных пространств, построение свободных групп и модулей, прямые и обратные пределы. Понятия предела и копредела обобщают некоторые из вышеперечисленных.
Универсальные конструкции часто порождают пары сопряженных функторов .
Компьютерные реализации [ править ]
Функторы иногда появляются в функциональном программировании . Например, в языке программирования Haskell есть класс Functor где fmap — политипическая функция , используемая для отображения функций ( морфизмы на Hask , категория типов Haskell) [9] между существующими типами и функциями между некоторыми новыми типами. [10]
См. также [ править ]
Примечания [ править ]
- ^ Мак Лейн, Сондерс (1971), Категории для работающего математика , Нью-Йорк: Springer-Verlag, стр. 30, ISBN 978-3-540-90035-1
- ^ Карнап, Рудольф (1937). Логический синтаксис языка , Рутледж и Кеган, стр. 13–14.
- ^ Джейкобсон (2009) , с. 19, деф. 1.2.
- ^ Джейкобсон (2009) , стр. 19–20.
- ^ Попеску, Николае; Попеску, Лилиана (1979). Теория категорий . Дордрехт: Спрингер. п. 12. ISBN 9789400995505 . Проверено 23 апреля 2016 г.
- ^ Мак Лейн, Сондерс ; Мурдейк, Ике (1992), Пучки в геометрии и логике: первое введение в теорию топоса , Springer, ISBN 978-0-387-97710-2
- ^ Hazewinkel, Michiel ; Gubareni, Nadezhda Mikhaĭlovna ; Gubareni, Nadiya ; Kirichenko, Vladimir V. (2004), Algebras, rings and modules , Springer, ISBN 978-1-4020-2690-4
- ^ Джейкобсон (2009) , с. 20, упр. 2.
- ^ Не совсем ясно, действительно ли типы данных Haskell образуют категорию. См. https://wiki.haskell.org/Hask для получения более подробной информации.
- ^ см . https://wiki.haskell.org/Category_theory/Functor#Functors_in_Haskell . Дополнительную информацию
Ссылки [ править ]
- Джейкобсон, Натан (2009), Основная алгебра , том. 2 (2-е изд.), Дувр, ISBN 978-0-486-47187-7 .
Внешние ссылки [ править ]
- «Функтор» , Математическая энциклопедия , EMS Press , 2001 [1994]
- см. функтор в n Lab и обсуждаемые там варианты и ссылки на них.
- Андре Жойал , CatLab , вики-проект, посвященный изложению категориальной математики.
- Хиллман, Крис (2001). «Категорический букварь» . CiteSeerX 10.1.1.24.3264 . Архивировано из оригинала 3 мая 1997 г.
- Дж. Адамек, Х. Херрлих, Г. Стекер, Абстрактные и конкретные категории - Радость кошек. Архивировано 21 апреля 2015 г. в Wayback Machine.
- Стэнфордская энциклопедия философии : « Теория категорий » — Жан-Пьер Маркиз. Обширная библиография.
- Список научных конференций по теории категорий
- Баэз, Джон, 1996, « Повесть о n -категориях». Неофициальное введение в категории высшего порядка.
- WildCats — это пакет теории категорий для Mathematica . Манипулирование и визуализация объектов, морфизмов , категорий, функторов, естественных преобразований , универсальных свойств .
- The catsters — канал на YouTube, посвященный теории категорий.
- Видеоархив записей выступлений по категориям, логике и основам физики.
- Интерактивная веб-страница , генерирующая примеры категориальных конструкций в категории конечных множеств.





























































