Неаналитическая гладкая функция
В математике ( гладкие функции также называемые бесконечно дифференцируемыми функциями) и аналитические функции — два очень важных типа функций . Легко доказать, что любая аналитическая функция вещественного аргумента является гладкой. Обратное неверно , как показывает приведенный ниже контрпример .
Одним из наиболее важных приложений гладких функций с компактным носителем является построение так называемых мягчителей , которые играют важную роль в теориях обобщенных функций , таких как Лорана Шварца теория распределений .
Существование гладких, но неаналитических функций представляет собой одно из главных различий между дифференциальной геометрией и аналитической геометрией . В терминах теории пучков это различие можно сформулировать следующим образом: пучок дифференцируемых функций на дифференцируемом многообразии тонкий , в отличие от аналитического случая.
Приведенные ниже функции обычно используются для построения разбиений единицы на дифференцируемых многообразиях.
Пример функции
[ редактировать ]Определение функции
[ редактировать ]
Рассмотрим функцию
определено для каждого действительного числа x .
Функция гладкая
[ редактировать ]Функция f имеет непрерывные производные всех порядков в каждой точке x вещественной прямой . Формула для этих производных:
где p n ( x ) — многочлен степени n − 1 , заданный рекурсивно как p 1 ( x ) = 1 и
для любого положительного целого числа n . Из этой формулы не совсем ясно, что производные непрерывны в точке 0; это следует из одностороннего предела
для любого неотрицательного целого числа m .
Подробное доказательство гладкости |
|---|
Функция не является аналитической
[ редактировать ]Как было замечено ранее, функция f является гладкой, и все ее производные в начале координат равны 0. Следовательно, ряд Тейлора функции f в начале координат всюду сходится к нулевой функции ,
и поэтому ряд Тейлора не равен f ( x ) при x > 0. Следовательно, f не является аналитическим в начале координат.
Функции плавного перехода
[ редактировать ]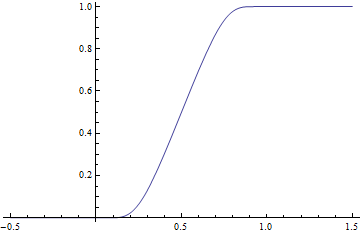
Функция
имеет строго положительный знаменатель всюду на вещественной прямой, следовательно, g также гладкая. Кроме того, g ( x ) = 0 для x ≤ 0 и g ( x ) = 1 для x ≥ 1, следовательно, это обеспечивает плавный переход с уровня 0 на уровень 1 в единичном интервале [0, 1]. Чтобы иметь плавный переход в вещественном интервале [ a , b ] с a < b , рассмотрим функцию
Для действительных чисел a < b < c < d гладкая функция
равен 1 на замкнутом интервале [ b , c ] и исчезает вне открытого интервала ( a , d ), следовательно, он может служить функцией рельефа .
Гладкая функция, которая нигде не является аналитической.
[ редактировать ]
Более патологический пример — бесконечно дифференцируемая функция, не являющаяся аналитической ни в какой точке . Его можно построить с помощью ряда Фурье следующим образом. Определить для всех
Начиная с сериала сходится для всех , эта функция, как легко видеть, принадлежит классу C ∞ , с помощью стандартного индуктивного применения М-теста Вейерштрасса для демонстрации равномерной сходимости каждой серии производных.
Сейчас мы покажем, что не является аналитическим ни при каком двоично-рациональном кратном π, т. е. при любом с и . Поскольку сумма первых термин аналитичен, нам нужно только рассмотреть , сумма членов с . Для всех порядков вывода с , и у нас есть
где мы использовали тот факт, что для всех , а первую сумму мы ограничили снизу членом с . Как следствие, при любом таком
так что сходимости ряда Тейлора радиус в равен 0 по формуле Коши-Адамара . Поскольку множество аналитичности функции является открытым множеством и поскольку двоично-рациональные числа плотны , заключаем, что , и, следовательно, , нигде не является аналитическим в .
Приложение к ряду Тейлора
[ редактировать ]Для каждой последовательности α 0 , α 1 , α 2 , . . . действительных или комплексных чисел следующая конструкция показывает существование гладкой функции F на действительной прямой, которая имеет эти числа как производные в начале координат. [1] В частности, каждая последовательность чисел может выступать в качестве коэффициентов ряда Тейлора гладкой функции. Этот результат известен как лемма Бореля в честь Эмиля Бореля .
Используя функцию плавного перехода g , как указано выше, определите
Эта функция h также является гладкой; он равен 1 на отрезке [−1,1] и обращается в нуль вне отрезка (−2,2). Используя h , определите для каждого натурального числа n (включая ноль) гладкую функцию
что совпадает с мономом x н на [−1,1] и обращается в нуль вне интервала (−2,2). Следовательно, k -я производная ψ n в начале координат удовлетворяет условию
а из теоремы об ограниченности следует, что ψ n и каждая производная от ψ n ограничены. Следовательно, константы
включающие верхнюю норму ψ производные, являются n и ее первые n четко определенными действительными числами. Определите масштабируемые функции
Путем многократного применения правила цепочки ,
и, используя предыдущий результат для k -й производной ψ n в нуле,
Осталось показать, что функция
четко определена и может дифференцироваться почленно бесконечное число раз. [2] Для этого заметим, что для каждого k
где оставшийся бесконечный ряд сходится по критерию отношения .
Применение к более высоким измерениям
[ редактировать ]
Для каждого радиуса r > 0
с евклидовой нормой || х || определяет гладкую функцию в n -мерном евклидовом пространстве с опорой в шаре радиуса r , но .
Комплексный анализ
[ редактировать ]Эта патология не может возникнуть при дифференцируемых функциях комплексной переменной, а не действительной переменной. Действительно, все голоморфные функции аналитичны , так что неспособность функции f, определенной в этой статье, быть аналитической, несмотря на ее бесконечно дифференцируемую, является указанием на одно из самых драматических различий между анализом с действительными переменными и анализом с комплексными переменными.
Заметим, что хотя функция f имеет производные всех порядков по вещественной прямой, аналитическое продолжение f > 0 от положительной полупрямой x на комплексную плоскость , т. е. функция
имеет существенную особенность в начале координат и, следовательно, не является даже непрерывным и тем более аналитическим. По великой теореме Пикара оно достигает каждого комплексного значения (за исключением нуля) бесконечное число раз в каждой окрестности начала координат.
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Упражнение 12 на странице 418 в книге Вальтера Рудина « Реальный и комплексный анализ» . МакГроу-Хилл, Нью-Дели, 1980 г., ISBN 0-07-099557-5
- ^ См., например, главу V, раздел 2, теорему 2.8 и следствие 2.9 о дифференцируемости пределов последовательностей функций из Аманн, Герберт; Эшер, Иоахим (2005), Анализ I , Базель: Birkhäuser Verlag , стр. 373–374, ISBN 3-7643-7153-6



















































