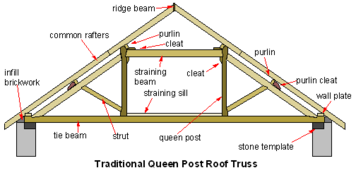
ферма
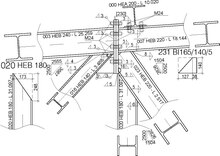
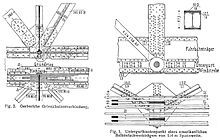
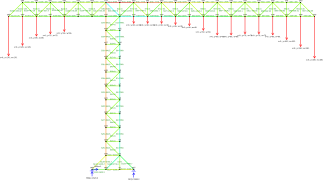
Ферма — это совокупность таких элементов , как балки , соединенных узлами , которые создают жесткую конструкцию. [1]
В инженерии ферма — это конструкция , которая «состоит только из элементов с двумя силами, причем элементы организованы так, что вся сборка в целом ведет себя как единый объект». [2] «Элемент с двумя силами» — это конструктивный элемент, в котором сила прикладывается только к двум точкам. Хотя это строгое определение позволяет элементам иметь любую форму, соединенную в любой стабильной конфигурации, фермы обычно состоят из пяти или более треугольных элементов, построенных из прямых элементов, концы которых соединены в узлах, называемых узлами .
В этом типичном контексте считается, что внешние силы и реакции на эти силы действуют только в узлах и приводят к возникновению сил в элементах, которые являются либо растягивающими , либо сжимающими . Для прямых элементов моменты ( крутящие моменты ) явно исключаются, потому что и только потому, что все соединения в ферме рассматриваются как вращающиеся , что необходимо для того, чтобы звенья были элементами с двумя силами.
Плоская ферма — это ферма, в которой все элементы и узлы лежат в двухмерной плоскости, тогда как в пространственной раме элементы и узлы простираются в трех измерениях . Верхние балки фермы называются «верхними поясами» и обычно находятся в сжатом состоянии , нижние балки называются «нижними поясами» и обычно находятся в растяжении . Внутренние балки называются перегородками , а области внутри перемычек называются панелями . [3] или из графической статики (см. диаграмму Кремоны ) «полигоны». [4]
Этимология
[ редактировать ]Ферма происходит от старофранцузского слова trousse , датируемого примерно 1200 годом нашей эры, что означает «совокупность связанных вместе вещей». [5] [6] Термин «ферма» часто используется для описания любой сборки элементов, таких как несущая рама. [7] [8] или пара стропил. [9] [10] Одно из инженерных определений звучит так: «Ферма представляет собой единую плоскую конструкцию, состоящую из отдельных конструктивных элементов [sic], соединенных на своих концах и образующих ряд треугольников [sic], охватывающих большое расстояние». [11]
Характеристики
[ редактировать ]
Ферма обычно (но не обязательно) состоит из прямых элементов, соединенных в местах соединений, традиционно называемых точками панели . Фермы обычно (но не обязательно) [12] ) состоит из треугольников из-за структурной устойчивости этой формы и конструкции. Треугольник — простейшая геометрическая фигура, которая не меняет формы при фиксированных длинах сторон. [13] Для сравнения: и углы, и длины четырехсторонней фигуры должны быть фиксированными, чтобы она сохраняла свою форму.
Простая ферма
[ редактировать ]
Самая простая форма фермы — это один треугольник. Этот тип фермы встречается в каркасной крыше, состоящей из стропил и потолочной балки . [14] и в других механических конструкциях, таких как велосипеды и самолеты. Из-за стабильности этой формы и методов анализа, используемых для расчета сил внутри нее, ферма, состоящая полностью из треугольников, известна как простая ферма. [15] Однако простая ферма часто определяется более ограничительно, требуя, чтобы она могла быть построена путем последовательного добавления пар элементов, каждый из которых соединен с двумя существующими соединениями и друг с другом, образуя новое соединение, и это определение не требует простой фермы. состоять только из треугольников. [12] Традиционная велосипедная рама ромбовидной формы, в которой используются два соединенных треугольника, является примером простой фермы. [16]
Плоская ферма
[ редактировать ]
Плоская ферма лежит в одной плоскости . [15] Плоские фермы обычно используются параллельно для формирования крыш и мостов. [17]
Глубина фермы, или высота между верхним и нижним поясами, делает ее эффективной структурной формой. Сплошная балка или балка равной прочности будет иметь значительный вес и стоимость материала по сравнению с фермой. Для данного пролета более глубокая ферма потребует меньше материала в поясах и больше материала в вертикалях и диагоналях. Оптимальная глубина фермы максимизирует эффективность. [18]
Пространственная рамная ферма
[ редактировать ]Ферма с пространственным каркасом представляет собой трехмерный каркас из элементов, закрепленных на концах. Форма тетраэдра — это простейшая космическая ферма, состоящая из шести элементов, соприкасающихся в четырех стыках. [15] Крупные плоские конструкции могут быть составлены из тетраэдров с общими ребрами, а также используются в конструкциях оснований крупных отдельно стоящих опор ЛЭП.
Простой тетраэдр
Схема пространственного каркаса, например, используемого для крыши
Этот электрический столб представляет собой трехмерную ферменную конструкцию.
Типы
[ редактировать ]- Дополнительные типы ферм см. в разделе « Типы ферм, используемых в мостах» .
Существует два основных типа ферм:
- Скатная ферма, или обычная ферма, отличается треугольной формой. Чаще всего его используют для строительства кровли. Некоторые распространенные фермы названы в соответствии с их «веб-конфигурацией». Размер хорды и конфигурация стенки определяются пролетом, нагрузкой и расстоянием.
- Ферма с параллельными поясами, или плоская ферма, получила свое название от параллельных верхнего и нижнего поясов. Его часто используют для устройства полов.
Комбинация этих двух элементов представляет собой усеченную ферму, используемую в конструкции вальмовой крыши. Деревянная ферма, соединенная металлическими пластинами, представляет собой ферму крыши или пола, деревянные элементы которой соединены металлическими соединительными пластинами .
Уоррен ферма
[ редактировать ]Элементы фермы образуют ряд равносторонних треугольников, чередующихся вверх и вниз.
Октетная ферма
[ редактировать ]Элементы фермы состоят из всех эквивалентных равносторонних треугольников. Минимальный состав — два правильных тетраэдра вместе с октаэдром. Они заполняют трехмерное пространство в самых разных конфигурациях.
Ферма Пратта
[ редактировать ]
Ферма Пратта была запатентована в 1844 году двумя инженерами-железнодорожниками Бостона . [19] Калеб Пратт и его сын Томас Уиллис Пратт . [20] В конструкции используются вертикальные элементы для сжатия и диагональные элементы для реагирования на растяжение . Конструкция фермы Пратта оставалась популярной, поскольку проектировщики мостов перешли от дерева к железу и от железа к стали. [21] Эта продолжающаяся популярность фермы Пратта, вероятно, связана с тем, что конфигурация элементов означает, что более длинные диагональные элементы растягиваются только под воздействием гравитационной нагрузки. Это позволяет использовать эти элементы более эффективно, поскольку эффекты гибкости, связанные с короблением под сжимающими нагрузками (которые усугубляются длиной элемента), обычно не влияют на конструкцию. Следовательно, для заданной плоской фермы с фиксированной глубиной конфигурация Пратта обычно является наиболее эффективной при статической вертикальной нагрузке.
Мост Южно-Тихоокеанской железной дороги в Темпе , штат Аризона, представляет собой ферменный мост длиной 393 метра (1291 фут), построенный в 1912 году. [22] [23] Конструкция состоит из девяти пролетов фермы Пратта различной длины. Мост используется до сих пор.
В конструкции крыла Wright Flyer использовалась ферма Pratt, поскольку минимизация длины сжимающих элементов позволила снизить аэродинамическое сопротивление . [24]
Тетива фермы
[ редактировать ]
Названные в честь своей формы, тетивные фермы впервые использовались для арочных ферменных мостов , которые часто путают с мостами с завязанными арками .
Тысячи тетивных ферм использовались во время Второй мировой войны для поддержания изогнутых крыш авиационных ангаров и других военных зданий. Существует множество вариаций расположения элементов, соединяющих узлы верхней дуги с узлами нижней прямой последовательности элементов, от почти равнобедренных треугольников до варианта фермы Пратта.
Королевская ферма
[ редактировать ]
Один из самых простых в реализации стилей ферм, королевский столб состоит из двух угловых опор, опирающихся на общую вертикальную опору.
Ферма королевской стойки, иногда королевская стойка или королевская стойка , похожа на ферму королевской стойки тем, что внешние опоры расположены под углом к центру конструкции. Основное отличие заключается в горизонтальном расширении в центре, которое опирается на действие луча для обеспечения механической устойчивости. Этот тип фермы подходит только для относительно коротких пролетов. [25]
Чечевицеобразная ферма
[ редактировать ]
Чечевицеобразные фермы, запатентованные в 1878 году Уильямом Дугласом (хотя мост без Гауна 1823 года был первым такого типа), имеют изогнутые верхний и нижний пояса фермы, образующие форму линзы. Мост с двояковыпуклой фермой представляет собой конструкцию моста, включающую двояковыпуклую ферму, идущую над и под дорожным полотном.
Решётчатая ферма города
[ редактировать ]
Американский архитектор Итиэль Таун спроектировал городскую решетчатую ферму как альтернативу тяжелым деревянным мостам. В его конструкции, запатентованной в 1820 и 1835 годах, используются удобные в обращении доски, расположенные по диагонали с небольшими промежутками между ними, образующие решетку .
Ферма Виренделя
[ редактировать ]
Ферма Виренделя представляет собой конструкцию, элементы которой не имеют треугольной формы, а образуют прямоугольные проемы, и представляет собой раму с неподвижными соединениями, способными передавать и сопротивляться изгибающим моментам . Как таковая, она не соответствует строгому определению фермы (поскольку она содержит элементы, не обладающие двумя силами): обычные фермы включают элементы, которые, как обычно предполагается, имеют шарнирные соединения, при этом подразумевается, что на соединенных концах не существует моментов. Этот стиль конструкции был назван в честь бельгийского инженера Артура Виренделя . [26] который разработал конструкцию в 1896 году. Ее используют для мостов редко из-за более высокой стоимости по сравнению с треугольной фермой.
Полезность конструкции этого типа в зданиях заключается в том, что большая часть внешней оболочки остается свободной и может использоваться для оконных и дверных проемов. В некоторых случаях это предпочтительнее системы с раскосами, в которой диагональные раскосы оставляют некоторые области закрытыми.
Статика
[ редактировать ]
Ферма, которая, как предполагается, состоит из элементов, соединенных посредством штифтовых соединений и поддерживаемых с обоих концов посредством шарнирных соединений и роликов, называется статически определенной . Законы Ньютона применимы к конструкции в целом, а также к каждому узлу или суставу. Чтобы любой узел, на который может действовать внешняя нагрузка или сила, оставался неподвижным в пространстве, должны выполняться следующие условия: суммы всех (горизонтальных и вертикальных) сил, а также всех моментов, действующих вокруг узла, равны нулю. Анализ этих условий в каждом узле дает величину сил сжатия или растяжения.
Фермы, которые поддерживаются более чем в двух положениях, считаются статически неопределимыми , и применения одних только законов Ньютона недостаточно для определения сил на стержнях.
Чтобы ферма с элементами, соединенными штифтами, была устойчивой, она не обязательно должна полностью состоять из треугольников. [12] С математической точки зрения существует следующее необходимое условие устойчивости простой фермы:
где m — общее количество элементов фермы, j — общее количество соединений, а r — количество реакций (обычно равное 3) в двумерной конструкции.
Когда Ферма называется статически определенной , поскольку ( m +3) внутренние силы стержня и реакции опоры могут быть полностью определены с помощью 2 j -уравнений равновесия , если мы знаем внешние нагрузки и геометрию фермы. Учитывая определенное количество соединений, это минимальное количество элементов в том смысле, что если какой-либо элемент будет удален (или выйдет из строя), то ферма в целом выйдет из строя. Хотя соотношение (а) необходимо, оно недостаточно для обеспечения устойчивости, которая также зависит от геометрии фермы, условий опоры и несущей способности элементов.
Некоторые конструкции построены с количеством элементов фермы, превышающим это минимальное значение. Эти структуры могут выжить, даже если некоторые из членов потерпят неудачу. Силы их элементов зависят от относительной жесткости элементов в дополнение к описанному условию равновесия.
Анализ
[ редактировать ]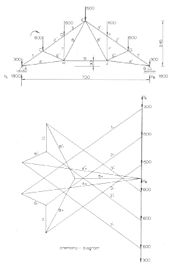
Поскольку силы в каждой из двух основных балок по существу плоские, ферма обычно моделируется как двумерная плоская рама. Однако при наличии значительных сил, выходящих за пределы плоскости, конструкцию необходимо моделировать как трехмерное пространство.
При анализе ферм часто предполагается, что нагрузки прикладываются только к стыкам, а не к промежуточным точкам вдоль элементов. Вес элементов часто незначителен по сравнению с приложенными нагрузками, поэтому его часто не учитывают; в качестве альтернативы половина веса каждого элемента может быть приложена к двум его концевым соединениям. При условии, что элементы длинные и тонкие, моменты, передаваемые через соединения, незначительны, и соединения можно рассматривать как « шарниры » или «штифтовые соединения».
Согласно этим упрощающим предположениям, каждый элемент фермы подвергается действию чистых сил сжатия или чистого растяжения – сдвиг, изгибающий момент и другие более сложные напряжения практически равны нулю. Фермы физически прочнее, чем другие способы расположения элементов конструкции, поскольку почти каждый материал может выдерживать гораздо большую нагрузку при растяжении или сжатии, чем при сдвиге, изгибе, кручении или других видах силы.
Эти упрощения облегчают анализ ферм. Структурный анализ ферм любого типа можно легко выполнить с использованием матричного метода, такого как прямой метод жесткости , метод гибкости или метод конечных элементов .
Силы в членах
[ редактировать ]На иллюстрации представлена простая статически определимая плоская ферма с 9 шарнирами и (2 x 9) − 3 = 15 элементами. Внешние нагрузки сосредоточены в наружных соединениях. Поскольку это симметричная ферма с симметричными вертикальными нагрузками, реактивные силы в точках A и B вертикальны, равны и составляют половину общей нагрузки.
Внутренние силы в элементах фермы можно рассчитать различными способами, в том числе графическими:
- Схема Кремоны
- Диаграмма Кульмана
- Аналитический метод Риттера ( метод сечений )
Дизайн членов
[ редактировать ]Ферму можно рассматривать как балку , перемычка которой состоит из ряда отдельных элементов, а не из сплошной пластины. В ферме нижний горизонтальный элемент ( нижний пояс ) и верхний горизонтальный элемент ( верхний пояс ) несут растяжение и сжатие , выполняя ту же функцию, что и полки двутавровой балки . Какая хорда несет напряжение, а какая сжатие, зависит от общего направления изгиба . В ферме, изображенной выше справа, нижний пояс находится в растяжении, а верхний пояс - в сжатии.
Диагональные и вертикальные элементы образуют стенку фермы и несут напряжение сдвига . По отдельности они также находятся на растяжении и сжатии, точное распределение сил зависит от типа фермы и опять же от направления изгиба. В ферме, показанной выше справа, вертикальные элементы находятся в растяжении, а диагонали — в сжатии.
Помимо восприятия статических сил, элементы выполняют дополнительные функции стабилизации друг друга, предотвращая коробление . На соседнем рисунке верхний пояс защищен от прогиба благодаря наличию распорок и жесткости элементов перемычки.
Включение показанных элементов в значительной степени является инженерным решением, основанным на экономике, поскольку оно представляет собой баланс между затратами на сырье, изготовление за пределами площадки, транспортировку компонентов, монтаж на месте, доступность оборудования и стоимость рабочей силы. В других случаях внешний вид конструкции может иметь большее значение и, таким образом, влиять на проектные решения, выходящие за рамки простых экономических вопросов. Современные материалы, такие как предварительно напряженный бетон , и методы изготовления, такие как автоматизированная сварка , существенно повлияли на конструкцию современных мостов .
Как только сила, действующая на каждый элемент, станет известна, следующим шагом будет определение поперечного сечения отдельных элементов фермы. Для элементов, находящихся под напряжением, площадь поперечного сечения A можно найти по формуле A = F × γ/σy , где F — сила, действующая на элемент, γ — коэффициент запаса прочности (обычно 1,5, но в зависимости от строительных норм ), а σy — предел текучести используемой стали.
Сжимаемые элементы также должны быть спроектированы так, чтобы не допустить коробления.
Вес элемента фермы напрямую зависит от его поперечного сечения — этот вес частично определяет, насколько прочными должны быть другие элементы фермы. Чтобы придать одному элементу большее поперечное сечение, чем на предыдущей итерации, необходимо также предоставить другим элементам большее поперечное сечение, чтобы выдержать больший вес первого элемента - нужно пройти еще одну итерацию, чтобы точно определить, насколько больше нужно другим элементам. быть. Иногда проектировщик проходит несколько итераций процесса проектирования, чтобы прийти к «правильному» сечению для каждого элемента. С другой стороны, уменьшение размера одного элемента по сравнению с предыдущей итерацией просто приводит к тому, что другие элементы имеют больший (и более дорогой) запас прочности, чем это технически необходимо, но не требует еще одной итерации для поиска сборной фермы.
Влияние веса отдельных элементов фермы большого размера, например моста, обычно незначительно по сравнению с силой внешних нагрузок.
Проектирование соединений
[ редактировать ]После определения минимального поперечного сечения элементов последним шагом в проектировании фермы будет детализация болтовых соединений , например, с учетом напряжения сдвига болтовых соединений, используемых в соединениях. В зависимости от потребностей проекта внутренние соединения (стыки) ферм могут быть выполнены жесткими, полужесткими или шарнирными. Жесткие соединения могут обеспечивать передачу изгибающих моментов, приводящую к развитию вторичных изгибающих моментов в элементах.
Приложения
[ редактировать ]
Каркасные конструкции столбов
[ редактировать ]Соединения компонентов имеют решающее значение для структурной целостности каркасной системы. В зданиях с большими деревянными фермами со свободными пролетами наиболее важными являются соединения между фермой и ее опорами. Помимо сил, вызванных силой тяжести (т.н. несущих нагрузок), эти соединения должны противостоять силам сдвига, действующим перпендикулярно плоскости фермы, и силам подъема, вызванным ветром. В зависимости от общей конструкции здания соединения могут также потребоваться для передачи изгибающего момента.
Деревянные стойки позволяют создавать прочные, прямые и недорогие соединения между большими фермами и стенами. Точные детали соединений стойки с фермой варьируются от проектировщика к проектировщику и могут зависеть от типа стойки. Столбы из цельного пиломатериала и клееного бруса обычно имеют надрезы для образования несущей поверхности фермы. Ферма упирается в пазы и закрепляется болтами. Для увеличения возможностей передачи нагрузки на соединение можно добавить специальную пластину/кронштейн. При использовании стоек с механическим ламинированием ферма может опираться на укороченный внешний слой или на укороченный внутренний слой. В более позднем сценарии болты подвергаются двойному сдвигу и представляют собой очень эффективное соединение.
Галерея
[ редактировать ]
Башня Гонконгского банка Китая имеет видимую снаружи ферменную конструкцию.
Главное здание HSBC в Гонконге имеет видимую снаружи ферменную конструкцию.
Опорная конструкция под мостом через гавань Окленда
Вид на мост через гавань Окленда с острова Вочман на западе.
Маленький Бельтский мост : ферменный мост в Дании.
Сборные стальные фермы крыши с носовой тетивой, построенные в 1942 году для объектов военного ведомства в Северной Австралии.
Ферма крыши бокового здания аббатства Клюни , Франция
Космическая ферма, несущая пол в торговом центре Woodlands.
Трехмерная ферменная конструкция
Пример расчета сил фермы, выполненный программой, использующей матричный метод решения Гаусса.
См. также
[ редактировать ]- Коричневая ферма
- Выпуклые однородные соты
- Геодезический купол
- Решетчатая башня
- Слесарь по фермам
- Стресс:
- Строительная механика
- Конструкционная сталь
- Тенсегрити
- Анкерный стержень
Ссылки
[ редактировать ]- ^ «Определение ФЕРМЫ» . 7 марта 2024 г.
- ^ Плеша, Майкл Э.; Грей, Гэри Л.; Костанцо, Франческо (2013). Инженерная механика: Статика (2-е изд.). Нью-Йорк: McGraw-Hill Companies Inc., стр. 364–407. ISBN 978-0-07-338029-2 .
- ^ Чинг, Фрэнк. Визуальный словарь архитектуры . 2-е изд. Хобокен, Нью-Джерси: Wiley, 2012. 277. Печать. ISBN 9780470648858
- ^ Боу Р.Х., Экономика строительства каркасных конструкций. Спон, Лондон, 1873 г.
- ^ Рейф, Ф., etymonline.com (1965).
- ^ Оксфордский словарь английского языка
- ^ Благородный, Аллен Джордж. Традиционные здания: глобальный обзор структурных форм и культурных функций. Лондон: IB Tauris; 2007. 115. ISBN 1845113055
- ^ Дэвис, Николас и Эркки Йокиниеми. Словарь архитектуры и строительства. Амстердам: Elsevier/Architectural Press, 2008. 394. ISBN 0750685026
- ^ Дэвис, Николас и Эркки Йокиниеми. Иллюстрированный карманный словарь архитектора. Оксфорд: Архитектурная пресса, 2011. 121. ISBN 0080965377
- ^ Крэбб, Джордж. Универсальный технологический словарь или знакомое объяснение терминов, используемых во всех искусствах и науках...», Том 1, Лондон: 1823. Пары.
- ^ Шекхар, Р.К. Чандра. Академический словарь гражданского строительства. Дели: Isha Books, 2005. 431. ISBN 8182051908
- ^ Jump up to: а б с Пиво, Ферд; Джонстон, Расс (2013). Векторная механика для инженеров: Статика (10-е изд.). Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл. стр. 285–313. ISBN 978-0-07-740228-0 .
- ^ Рикер, Натан Клиффорд (1912) [1912]. Курс по проектированию и строительству крыш . Нью-Йорк: Дж. Уайли и сыновья. п. 12 . Проверено 15 августа 2008 г.
- ^ Маджиннис, Оуэн Бернард (1903). Каркас крыши стал проще (2-е изд.). Нью-Йорк: Промышленная издательская компания. п. 9 . Проверено 16 августа 2008 г.
- ^ Jump up to: а б с Хиббелер, Рассел Чарльз (1983) [1974]. Инженерная механика-статика (3-е изд.). Нью-Йорк: Macmillan Publishing Co., Inc., стр. 199–224. ISBN 0-02-354310-8 .
- ^ Вингертер Р. и Лабоссьер П., ME 354, Лаборатория механики материалов: конструкции , Вашингтонский университет (февраль 2004 г.), стр. 1
- ^ Люблинер, Джейкоб; Пападопулос, Панайотис (23 октября 2016 г.). Введение в механику твердого тела: комплексный подход . Спрингер. ISBN 9783319188782 .
- ^ Мерриман, Мэнсфилд (1912) [192]. Карманный справочник американских инженеров-строителей . Нью-Йорк: Дж. Уайли и сыновья. п. 785 . Проверено 16 августа 2008 г.
Экономическая глубина фермы — это то, что позволяет свести материал моста к минимуму.
- ^ Мост Бетанга. Архивировано 9 июня 2011 г. в Wayback Machine в офисе наследия Нового Южного Уэльса ; получено 6 февраля 2008 г.
- ^ Краткая история крытых мостов в Теннесси в Министерстве транспорта Теннесси ; получено 6 февраля 2008 г.
- ^ Ферма Пратта. Архивировано 28 мая 2008 г. в Wayback Machine, любезно предоставлено Министерством транспорта Мэриленда ; получено 6 февраля 2008 г.
- ^ «1. Железнодорожный мост Южно-Тихоокеанского региона, мост Эш-авеню и мост Милл-авеню со стороны Темпе-Бьютта, смотрящий на северо-запад. - Восточный железнодорожный мост Аризоны, переправа через Солт-Ривер, Темпе, округ Марикопа, Аризона» . Библиотека Конгресса . Проверено 26 марта 2020 г.
- ^ Обзор исторической собственности Темпе. Архивировано 10 ноября 2007 г. в Wayback Machine в Историческом музее Темпе ; получено 6 февраля 2008 г.
- ^ Дарио Гаспарини, Университет Кейс Вестерн Резерв. Братья Райт и ферма Пратта , слайды презентации
- ^ Типы ферм крытого моста, заархивировано 12 мая 2008 г. в Wayback Machine.
- ^ Мосты Виренделя
| Базы данных органов управления : Национальные |
|---|
