Обработка сигналов
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
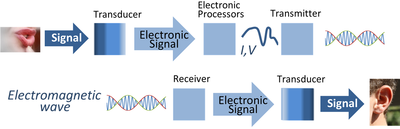


Обработка сигналов — это подобласть электротехники , которая фокусируется на анализе, изменении и синтезе сигналов , таких как звук , изображения , потенциальные поля , сейсмические сигналы , обработка альтиметрии и научные измерения . [1] Методы обработки сигналов используются для оптимизации передачи, эффективности цифрового хранения , коррекции искаженных сигналов, субъективного качества видео , а также для обнаружения или точного определения интересующих компонентов в измеренном сигнале. [2]
История
[ редактировать ]По мнению Алана В. Оппенгейма и Рональда В. Шафера , принципы обработки сигналов можно найти в классических методах численного анализа 17 века. Они также заявляют, что цифровое усовершенствование этих методов можно найти в цифровых системах управления 1940-х и 1950-х годов. [3]
В 1948 году Клод Шеннон написал влиятельную статью « Математическая теория связи », которая была опубликована в техническом журнале Bell System . [4] Этот документ заложил основу для дальнейшего развития систем информационной связи и обработки сигналов для передачи. [5]
Обработка сигналов достигла зрелости и процветания в 1960-х и 1970-х годах, а цифровая обработка сигналов стала широко использоваться с помощью специализированных микросхем цифровых сигнальных процессоров в 1980-х годах. [5]
Определение сигнала
[ редактировать ]Сигнал – это функция , где эта функция либо [6]
- детерминированный (тогда говорят о детерминированном сигнале) или
- путь , реализация случайного процесса
Категории
[ редактировать ]Аналоговый
[ редактировать ]Аналоговая обработка сигналов предназначена для сигналов, которые не были оцифрованы, как в большинстве радио- , телефонных и телевизионных систем 20-го века. Сюда входят как линейные электронные схемы, так и нелинейные. К первым относятся, например, пассивные фильтры , активные фильтры , аддитивные смесители , интеграторы и линии задержки . Нелинейные схемы включают компандоры , умножители ( смесители частоты , усилители, управляемые напряжением ), фильтры, управляемые напряжением , генераторы, управляемые напряжением , и системы фазовой автоподстройки частоты .
Непрерывное время
[ редактировать ]Непрерывная обработка сигналов предназначена для сигналов, которые изменяются с изменением непрерывной области (без учета некоторых отдельных точек прерывания).
Методы обработки сигналов включают временную область , частотную область и комплексную частотную область . Эта технология в основном обсуждает моделирование линейной, неизменной во времени непрерывной системы, интеграл реакции системы в нулевом состоянии, настройку функции системы и непрерывную временную фильтрацию детерминированных сигналов.
Дискретное время
[ редактировать ]Обработка сигналов в дискретном времени предназначена для дискретных сигналов, определенных только в дискретные моменты времени и, как таковые, квантованных по времени, но не по величине.
Аналоговая обработка сигналов с дискретным временем — это технология, основанная на электронных устройствах, таких как схемы выборки и хранения с временным разделением , аналоговые мультиплексоры , аналоговые линии задержки и сдвиговые регистры с аналоговой обратной связью . Эта технология была предшественницей цифровой обработки сигналов (см. ниже) и до сих пор используется при расширенной обработке сигналов гигагерцового диапазона.
Концепция обработки сигналов в дискретном времени также относится к теоретической дисциплине, которая устанавливает математическую основу для цифровой обработки сигналов без учета ошибок квантования .
Цифровой
[ редактировать ]Цифровая обработка сигналов — это обработка оцифрованных дискретизированных сигналов с дискретным временем. Обработка выполняется компьютерами общего назначения или цифровыми схемами, такими как ASIC , программируемые пользователем вентильные матрицы или специализированные процессоры цифровых сигналов (чипы DSP). Типичные арифметические операции включают операции с фиксированной и плавающей запятой , вещественные и комплексные значения, умножение и сложение. Другими типичными операциями, поддерживаемыми аппаратным обеспечением, являются циклические буферы и таблицы поиска . Примерами алгоритмов являются быстрое преобразование Фурье (БПФ), фильтр с конечной импульсной характеристикой (КИХ), фильтр с бесконечной импульсной характеристикой (БИХ) и адаптивные фильтры , такие как фильтры Винера и Калмана .
Нелинейный
[ редактировать ]Нелинейная обработка сигналов включает в себя анализ и обработку сигналов, создаваемых нелинейными системами, и может осуществляться во временной, частотной или пространственно-временной областях. [7] [8] Нелинейные системы могут создавать очень сложное поведение, включая бифуркации , хаос , гармоники и субгармоники , которые невозможно создать или проанализировать с помощью линейных методов.
Полиномиальная обработка сигналов — это тип нелинейной обработки сигналов, при котором полиномиальные системы можно интерпретировать как концептуально прямое расширение линейных систем на нелинейный случай. [9]
Статистический
[ редактировать ]Статистическая обработка сигналов — это подход, который рассматривает сигналы как случайные процессы , используя их статистические свойства для выполнения задач обработки сигналов. [10] Статистические методы широко используются в приложениях обработки сигналов. Например, можно смоделировать вероятностное распределение шума, возникающего при фотографировании изображения, и построить на основе этой модели методы уменьшения шума в полученном изображении.
Области применения
[ редактировать ]
- Обработка аудиосигнала - для электрических сигналов, представляющих звук, таких как речь или музыка. [11]
- Обработка изображений – в цифровых камерах, компьютерах и различных системах обработки изображений.
- Обработка видео – для интерпретации движущихся изображений.
- Беспроводная связь – генерация сигналов, демодуляция, фильтрация, выравнивание
- Системы управления
- Обработка массива – для обработки сигналов от массивов датчиков.
- Управление процессом – используются различные сигналы, включая стандартный токовый контур 4–20 мА.
- Сейсмология
- Извлечение функций , таких как понимание изображений и распознавание речи .
- Улучшение качества, такое как снижение шума , улучшение изображения и эхоподавление .
- Исходное кодирование, включая сжатие звука , сжатие изображений и сжатие видео .
- геномного сигнала Обработка [12]
- В геофизике обработка сигналов используется для усиления сигнала по сравнению с шумом при измерениях временных рядов геофизических данных. Обработка проводится либо во временной области , либо в частотной области , либо в обеих. [13] [14]
В системах связи обработка сигналов может происходить при:
- Уровень OSI 1 в семиуровневой модели OSI , физический уровень ( модуляция , выравнивание , мультиплексирование и т. д.);
- Уровень OSI 2, уровень канала передачи данных ( прямое исправление ошибок );
- Уровень OSI 6, уровень представления (исходное кодирование, включая аналого-цифровое преобразование и сжатие данных ).
Типовые устройства
[ редактировать ]- Фильтры — например, аналоговые (пассивные или активные) или цифровые ( КИХ , БИХ , частотные или стохастические фильтры и т. д.)
- Сэмплеры и аналого-цифровые преобразователи для сбора и восстановления сигналов , что включает в себя измерение физического сигнала, сохранение или передачу его в виде цифрового сигнала и, возможно, позднее восстановление исходного сигнала или его аппроксимации.
- Компрессоры сигналов
- Цифровые сигнальные процессоры (DSP)
Применяемые математические методы
[ редактировать ]- Дифференциальные уравнения [15]
- Рекуррентные отношения [16]
- Теория преобразования
- Частотно-временной анализ – для обработки нестационарных сигналов. [17]
- Спектральная оценка - для определения спектрального содержания (т. е. распределения мощности по частоте) временного ряда. [18]
- Статистическая обработка сигналов – анализ и извлечение информации из сигналов и шума на основе их стохастических свойств.
- Линейная теория нестационарных систем и теория преобразований
- Полиномиальная обработка сигналов - анализ систем, которые связывают входные и выходные данные с помощью полиномов.
- Идентификация системы [7] и классификация
- Исчисление
- Комплексный анализ [19]
- Векторные пространства и линейная алгебра [20]
- Функциональный анализ [21]
- Вероятность и случайные процессы [10]
- Теория обнаружения
- Теория оценки
- Оптимизация [22]
- Численные методы
- Временной ряд
- Интеллектуальный анализ данных - для статистического анализа отношений между большим количеством переменных (в данном контексте представляющих множество физических сигналов), для извлечения ранее неизвестных интересных закономерностей.
См. также
[ редактировать ]- Алгебраическая обработка сигналов
- Аудио фильтр
- Ограниченная вариация
- Цифровая обработка изображений
- Сжатие динамического диапазона , компандирование , ограничение и шумоподавление.
- Преобразование Фурье
- Теория информации
- Спектральный анализ методом наименьших квадратов
- Нелокальные средства
- Реверберация
- Чувствительность (электроника)
Ссылки
[ редактировать ]- ^ Сенгупта, Нандини; Сахидулла, Мэриленд; Саха, Гутам (август 2016 г.). «Классификация звуков легких с использованием кепстральных статистических характеристик». Компьютеры в биологии и медицине . 75 (1): 118–129. doi : 10.1016/j.compbiomed.2016.05.013 . ПМИД 27286184 .
- ^ Алан В. Оппенгейм и Рональд В. Шафер (1989). Дискретная обработка сигналов . Прентис Холл. п. 1. ISBN 0-13-216771-9 .
- ^ Оппенгейм, Алан В.; Шафер, Рональд В. (1975). Цифровая обработка сигналов . Прентис Холл . п. 5. ISBN 0-13-214635-5 .
- ^ «Математическая теория связи – революция CHM» . Компьютерная история . Проверено 13 мая 2019 г.
- ^ Перейти обратно: а б Пятьдесят лет обработки сигналов: Общество обработки сигналов IEEE и его технологии, 1948–1998 (PDF) . Общество обработки сигналов IEEE. 1998.
- ^ Бербер, С. (2021). Дискретные системы связи. Великобритания: Издательство Оксфордского университета, стр. 9, https://books.google.com/books?id=CCs0EAAAQBAJ&pg=PA9.
- ^ Перейти обратно: а б Биллингс, Ю.А. (2013). Идентификация нелинейных систем: методы NARMAX во временной, частотной и пространственно-временной областях . Уайли. ISBN 978-1-119-94359-4 .
- ^ Славинска, Дж.; Уурмазд, А.; Яннакис, Д. (2018). «Новый подход к обработке сигналов пространственно-временных данных». Семинар по статистической обработке сигналов (SSP) IEEE 2018 . IEEE Эксплор. стр. 338–342. дои : 10.1109/SSP.2018.8450704 . ISBN 978-1-5386-1571-3 . S2CID 52153144 .
- ^ В. Джон Мэтьюз; Джованни Л. Сикуранса (май 2000 г.). Полиномиальная обработка сигналов . Уайли. ISBN 978-0-471-03414-8 .
- ^ Перейти обратно: а б Шарф, Луи Л. (1991). Статистическая обработка сигналов: обнаружение, оценка и анализ временных рядов . Бостон : Аддисон-Уэсли . ISBN 0-201-19038-9 . ОСЛК 61160161 .
- ^ Саранги, Сусанта; Сахидулла, Мэриленд; Саха, Гутам (сентябрь 2020 г.). «Оптимизация набора фильтров на основе данных для автоматической проверки говорящих». Цифровая обработка сигналов . 104 : 102795. arXiv : 2007.10729 . Бибкод : 2020DSP...10402795S . дои : 10.1016/j.dsp.2020.102795 . S2CID 220665533 .
- ^ Анастасиу, Д. (2001). «Обработка геномного сигнала». Журнал обработки сигналов IEEE . 18 (4). ИИЭР: 8–20. Бибкод : 2001ISPM...18....8A . дои : 10.1109/79.939833 .
- ^ Телфорд, Уильям Мюррей; Гелдарт, LP; Шериф, Роберт Э. (1990). Прикладная геофизика . Издательство Кембриджского университета . ISBN 978-0-521-33938-4 .
- ^ Рейнольдс, Джон М. (2011). Введение в прикладную геофизику и геофизику окружающей среды . Уайли-Блэквелл . ISBN 978-0-471-48535-3 .
- ^ Патрик Гайдеки (2004). Основы цифровой обработки сигналов: теория, алгоритмы и проектирование аппаратного обеспечения . ИЭПП. стр. 40–. ISBN 978-0-85296-431-6 .
- ^ Шломо Энгельберг (8 января 2008 г.). Цифровая обработка сигналов: экспериментальный подход . Springer Science & Business Media. ISBN 978-1-84800-119-0 .
- ^ Боашаш, Буалем, изд. (2003). Частотно-временной анализ и обработка сигналов. Подробный справочник (1-е изд.). Амстердам: Эльзевир. ISBN 0-08-044335-4 .
- ^ Стойка, Петре; Моисей, Рэндольф (2005). Спектральный анализ сигналов (PDF) . Нью-Джерси: Прентис Холл.
- ^ Питер Дж. Шрайер; Луи Л. Шарф (4 февраля 2010 г.). Статистическая обработка сигналов комплексных данных: теория несобственных и нециклических сигналов . Издательство Кембриджского университета. ISBN 978-1-139-48762-7 .
- ^ Макс А. Литтл (13 августа 2019 г.). Машинное обучение для обработки сигналов: наука о данных, алгоритмы и вычислительная статистика . ОУП Оксфорд. ISBN 978-0-19-102431-3 .
- ^ Стивен Б. Дэмелин; Уиллард Миллер-младший (2012). Математика обработки сигналов . Издательство Кембриджского университета. ISBN 978-1-107-01322-3 .
- ^ Дэниел П. Паломар; Йонина К. Эльдар (2010). Выпуклая оптимизация в обработке сигналов и связи . Издательство Кембриджского университета. ISBN 978-0-521-76222-9 .
Дальнейшее чтение
[ редактировать ]- П. Стойка, Р. Моисей (2005). Спектральный анализ сигналов (PDF) . Нью-Джерси: Прентис Холл.
- Кей, Стивен М. (1993). Основы статистической обработки сигналов . Река Аппер-Сэддл, Нью-Джерси : Прентис-Холл . ISBN 0-13-345711-7 . ОСЛК 26504848 .
- Папулис, Афанасиос (1991). Вероятность, случайные величины и случайные процессы (третье изд.). МакГроу-Хилл. ISBN 0-07-100870-5 .
- Кайнам Томас Вонг [1] : Конспекты лекций по статистической обработке сигналов в Университете Ватерлоо, Канада.
- Али Х. Сайед , Адаптивные фильтры, Уайли, Нью-Джерси, 2008 г., ISBN 978-0-470-25388-5 .
- Томас Кайлат , Али Х. Сайед и Бабак Хассиби , Линейная оценка, Прентис-Холл, Нью-Джерси, 2000 г., ISBN 978-0-13-022464-4 .
Внешние ссылки
[ редактировать ]- Обработка сигналов для связи - бесплатный онлайн-учебник Паоло Прандони и Мартина Веттерли (2008 г.)
- Руководство для ученых и инженеров по цифровой обработке сигналов - бесплатный онлайн-учебник Стивена Смита
- Джулиус О. Смит III: Спектральная обработка аудиосигнала - бесплатный онлайн-учебник


