Логарифмическая линейка

— Логарифмическая линейка это с ручным управлением механический калькулятор , состоящий из передвижных линеек для оценки математических операций, таких как умножение , деление , возведение в степень , корни , логарифмы и тригонометрия . Это один из простейших аналоговых компьютеров . ^[1]^[2]

Скользящие линейки существуют в самых разных стилях и обычно имеют линейную, круглую или цилиндрическую форму. Логарифмические линейки, созданные для специализированных областей, таких как авиация или финансы, обычно имеют дополнительные шкалы, которые помогают в специализированных расчетах, характерных для этих областей. Логарифмическая линейка тесно связана с номограммами, используемыми для вычислений для конкретных приложений. Хотя логарифмическая линейка по названию и внешнему виду похожа на стандартную линейку , она не предназначена для измерения длины или рисования прямых линий. Он также не предназначен для сложения или вычитания, которое обычно выполняется с помощью других методов, например, с помощью счетов . Максимальная точность стандартных линейных логарифмических линеек составляет около трех десятичных значащих цифр, а используется экспоненциальная запись для отслеживания порядка величины результатов .

Английский математик и священнослужитель преподобный Уильям Отред и другие разработали логарифмическую линейку в 17 веке на основе новой работы по логарифмам Джона Непера . Это сделало вычисления более быстрыми и менее подверженными ошибкам, чем вычисления на бумаге . До появления научного карманного калькулятора он был наиболее часто используемым инструментом вычислений в науке и технике . ^[3] Простота использования, доступность и низкая стоимость логарифмической линейки привели к тому, что ее использование продолжало расти в течение 1950-х и 1960-х годов, даже несмотря на настольных электронных компьютеров постепенное внедрение . Но после того, как портативный научный калькулятор был представлен в 1972 году и стал недорогим в середине 1970-х годов, логарифмические линейки в значительной степени устарели , поэтому большинство поставщиков ушли из бизнеса.

В Соединенных Штатах логарифмическую линейку в просторечии называют скользящей палочкой . ^[4]^[5]

Основные понятия [ править ]

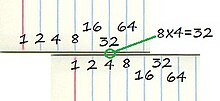
На шкале каждой линейки есть деления , помеченные предварительно вычисленными выходными данными различных математических функций , которые действуют как справочная таблица , которая сопоставляет положение на линейке с входными данными каждой функции. Вычисления, которые можно свести к простому сложению или вычитанию с использованием этих заранее вычисленных функций, можно решить, совместив две линейки и считав приблизительный результат.

Например, число, которое нужно умножить на одной линейке логарифмической шкалы, можно выровнять по началу другой такой линейки, чтобы суммировать их логарифмы. Затем, применив закон логарифма произведения , можно прочитать произведение двух чисел. Более сложные логарифмические линейки могут выполнять другие вычисления, такие как квадратные корни , экспоненты , логарифмы и тригонометрические функции .

Пользователь может оценить положение десятичной точки в результате, мысленно интерполируя между помеченными делениями. Научное обозначение используется для отслеживания десятичной точки для более точных вычислений. Шаги сложения и вычитания в расчете обычно выполняются в уме или на бумаге, а не на логарифмической линейке.

Компоненты [ править ]

Большинство логарифмических правил состоят из трех частей:

Каркас или основание – две полосы одинаковой длины, удерживаемые параллельно с зазором между ними.
Ползун – центральная полоса, сблокированная с рамой и способная перемещаться в продольном направлении относительно рамы.
Бегунок или стекло - внешняя скользящая деталь с тонкой линией, также известная как «курсор».

Некоторые логарифмические линейки (модели «дуплекс») имеют шкалы на обеих сторонах линейки и скользящей полосы, другие — на одной стороне внешних полосок и обеих сторонах скользящей полосы (которую для удобства обычно можно вытащить, перевернуть и снова вставить). ), третьи только с одной стороны («симплексные» правила). Скользящий курсор с вертикальной линией выравнивания используется для поиска соответствующих точек на шкалах, не прилегающих друг к другу или, в дуплексных моделях, находящихся по другую сторону линейки. Курсор также может фиксировать промежуточный результат по любой из шкал.

Десятилетия [ править ]

Шкалы могут быть сгруппированы по десятилетиям , где каждое десятилетие соответствует диапазону чисел, охватывающему соотношение 10 (т. е. диапазон от 10 ^н до 10 ^{п +1}). Например, диапазон от 1 до 10 — это одно десятилетие, а диапазон от 10 до 100 — другое десятилетие. Таким образом, однодекадные шкалы (названные C и D) варьируются от 1 до 10 по всей длине логарифмической линейки, а двухдекадные шкалы (названные A и B) варьируются от 1 до 100 по длине логарифмической линейки.

Операция [ править ]

Логарифмические шкалы [ править ]

Следующие логарифмические тождества преобразуют операции умножения и деления в сложение и вычитание соответственно:

\log(x\times y)=\log(x)+\log(y)\,,

\log(x/y)=\log(x)-\log(y)\,.

Умножение [ править ]

При использовании двух логарифмических шкал процесс позиционирования верхней шкалы начинается с метки нижней шкалы для $x$ соответствует сдвигу верхней логарифмической шкалы на расстояние $\log(x)$ . Это выравнивает номер каждой верхней шкалы. $y$ в зачете $\log(y)$ с номером нижней шкалы в положении $\log(x)+\log(y)$ . Потому что $\log(x)+\log(y)=\log(x\times y)$ , отметка на нижней шкале в этом положении соответствует $x\times y$ . при $x=2$ и $y=3$ Например, $, расположив верхнюю шкалу так, чтобы она начиналась с 2$ нижней шкалы , результат умножения $3\times2=6$ можно затем прочитать на нижней шкале под цифрой $3$ верхней шкалы :

Хотя приведенный выше пример относится к одному десятилетию, пользователи должны мысленно учитывать дополнительные нули при работе с несколькими десятилетиями. Например, ответ на вопрос $7\times2=14$ можно найти, сначала расположив верхнюю шкалу над цифрой 2 нижней шкалы, а затем считав отметку 1,4 на нижней двухдесятилетней шкале, где $7$ находится на верхней шкале:

Но поскольку $7$ находится над вторым набором чисел, это число необходимо умножить на $10$ . Таким образом, хотя ответ прямо читается как $1,4$ , правильный ответ — $1,4\times10 = 14$ .

В примере с еще большими числами, для умножения $88\times20$ , верхняя шкала снова располагается так, чтобы начинаться с $2$ на нижней шкале. Поскольку $2$ представляет $20$ , все числа в этой шкале умножаются на $10$ . Таким образом, любой ответ во втором наборе чисел умножается на $100$ . Поскольку $8,8$ на верхней шкале соответствует $88$ , ответ необходимо дополнительно умножить на $10$ . Ответ прямо гласит: $1,76$ . Умножьте на $100$ , а затем на $10,$ чтобы получить фактический ответ: $1760$ .

Как правило, $1$ вверху перемещается на фактор внизу, а ответ читается внизу, где другой фактор находится вверху. Это работает, поскольку расстояния от $отметки 1$ пропорциональны логарифмам отмеченных значений.

Дивизия [ править ]

На рисунке ниже показано вычисление $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}5,5 / 2$ . 2 $на$ на верхней шкале находится над $5,5$ нижней шкале. Полученное частное, $2,75$ , можно прочитать под $цифрой 1$ на верхней шкале :

Существует более одного метода деления, и представленный здесь метод имеет то преимущество, что конечный результат не может выйти за пределы шкалы, поскольку можно использовать $1$ на любом конце.

При более сложных вычислениях, включающих несколько множителей в числителе и знаменателе выражения, перемещение весов можно свести к минимуму путем чередования делений и умножений. Таким образом $5,5\times3 / 2$ будет рассчитываться как $5,5 / 2 \times3$ , а результат $8,25$ можно прочитать под цифрой $3$ на верхней шкале на рисунке выше, без необходимости регистрации промежуточного результата для $5.5 / 2$ .

Другие масштабы [ править ]

Эта логарифмическая линейка предназначена для получения нескольких значений: от шкалы C до шкалы D (умножить на 2), от шкалы D до шкалы C (делить на 2), шкал A и B (умножить и разделить на 4), шкал A и D. (квадраты и квадратные корни).

Помимо логарифмических шкал, некоторые логарифмические линейки имеют и другие математические функции, закодированные в других вспомогательных шкалах. Наиболее популярными являются тригонометрический , обычно синус и тангенс , десятичный логарифм (log 10 ) (для снятия логарифма значения по шкале множителя), натуральный логарифм (ln) и экспоненциальный ( e ^х) весы. Другие имеют шкалы для расчета гиперболических функций . В линейных правилах шкалы и их маркировка строго стандартизированы, при этом вариации обычно происходят только в зависимости от того, какие шкалы включены и в каком порядке. ^[6]

С, Д	однодекадные логарифмические шкалы, отдельные секции одинаковой длины, используемые вместе для умножения и деления, и обычно одна из них комбинируется с другой шкалой для других вычислений.
А, Б	двухдекадные логарифмические шкалы, две секции, каждая из которых составляет половину длины шкал C и D, используемые для нахождения квадратных корней и квадратов чисел.
К	трехдекадная логарифмическая шкала, три секции, каждая из которых составляет одну треть длины шкал C и D, используется для нахождения кубических корней и кубов чисел.
ЦФ, DF	сложенные версии шкал C и D, которые начинаются с пи ( π ), а не с единицы; это удобно в двух случаях. Во-первых, когда пользователь предполагает, что произведение будет близко к 10, и не уверен, будет ли оно немного меньше или чуть больше 10, сложенные весы исключают возможность выхода за пределы шкалы. Во-вторых, если начать с π, а не с квадратного корня из 10, умножение или деление на π (как это принято в научных и инженерных формулах) упрощается.
КИ, ДИ, КИФ, ДИФ	перевернутые шкалы, идущие справа налево, используемые для упрощения взаимного обмена ( 1 ⁄ x ) шагов
С	используется для нахождения синусов и косинусов по шкале C (или D)
Т, Т1, Т2	используется для нахождения тангенсов и котангенсов по шкалам C и CI (или D и DI).
Р1, Р2	масштаб квадратного корня – установка курсора на любое значение $r$ на R1 или R2 найдите ${\pi }r^{2}$ ( площадь круга радиуса $r$ ) под курсором на шкале DF
СТ, СТО	используется для синусов и тангенсов и малых углов преобразования в радианы. градусов
Ш, Ш1, Ш2	используется для поиска гиперболических синусов по шкале C (или D)
Ч	используется для нахождения гиперболических косинусов по шкале C (или D)
че	используется для нахождения гиперболических тангенсов по шкале C (или D)
л	линейная шкала, используемая для сложения, вычитания и (наряду со шкалами C и D) для нахождения логарифмов по основанию 10 и степеней 10.
LL0N (или LL/N) и LLN	бревно-бревно сложенное $e^{-x}$ и $e^{x}$ весы, для работы с логарифмами любых оснований и произвольных показателей. Обычно встречаются 4, 6 или 8 чешуек этого типа.
Лн	линейная шкала, используемая вместе со шкалами C и D для определения естественного (базового $e$ ) логарифмы и $e^{x}$
П	Пифагорейская шкала ${\sqrt {1-x^{2}}}$ (1) решить теорему Пифагора и (2) точно определить косинус для малых углов (по шкале S)

Чешуйки на передней и задней стороне логарифмической линейки Keuffel and Esser (K&E) 4181-3.

Двоичная логарифмическая линейка, изготовленная Гилсоном в 1931 году, выполняла функции сложения и вычитания, ограниченные дробями. ^[7]

Корни и силы [ править ]

Существуют однодекадные (C и D), двухдекадные (A и B) и трехдекадные (K) шкалы. Чтобы вычислить $x^{2}$ , например, найдите x на шкале D и прочтите его квадрат на шкале A. Обращение этого процесса позволяет найти квадратные корни, а также для степеней 3, 1/3, 2/3 и 3/2. Необходимо соблюдать осторожность, когда основание x находится более чем в одном месте шкалы. Например, на шкале А есть две девятки; чтобы найти квадратный корень из девяти, используйте первый; второй дает квадратный корень из 90.

Для $x^{y}$ проблемы, используйте шкалы LL. Если присутствует несколько шкал LL, используйте ту, на которой указан x . Сначала совместите крайнюю левую 1 на шкале C с x на шкале LL. Затем найдите y на шкале C и опуститесь на шкалу LL с х на ней. Эта шкала укажет ответ. Если y «зашкаливает», найдите $x^{y/2}$ и возведите его в квадрат, используя шкалы A и B, как описано выше. Альтернативно, используйте крайнюю правую 1 на шкале C и прочтите ответ по следующей более высокой шкале LL. Например, если совместить крайнюю правую цифру 1 на шкале C с цифрой 2 на шкале LL2, то цифра 3 на шкале C совпадет с цифрой 8 на шкале LL3.

Чтобы извлечь кубический корень с помощью логарифмической линейки только с шкалами C/D и A/B, совместите 1 на курсоре B с базовым числом на шкале A (как всегда, стараясь различать нижнюю и верхнюю половины шкалы A). шкала). Перемещайте слайдер до тех пор, пока число на шкале D, которое находится напротив 1 на курсоре C, не станет таким же, как число на курсоре B, которое находится напротив базового числа на шкале A. (Примеры: А 8, Б 2, С 1, Д 2; А 27, Б 3, С 1, Д 3.)

Корни квадратных уравнений [ править ]

Квадратные уравнения вида $ax^{2}+bx+c=0$ можно решить, предварительно приведя уравнение к виду $x^{2}-px+q=0$ (где $p=-b/a$ и $q=c/a$ ), а затем выравнивая индекс («1») шкалы C по значению $q$ по шкале Д. Затем курсор перемещают по правилу до тех пор, пока не будет найдено положение, в котором суммы чисел на шкалах CI и D равны $p$ . Эти два значения являются корнями уравнения.

Тригонометрия [ править ]

Шкалы S, T и ST используются для тригонометрических функций и кратных тригонометрическим функциям для углов в градусах.

Для углов от 5,7 до 90 градусов синусы находятся путем сравнения шкалы S со шкалой C (или D). (Во многих правилах закрытого тела шкала S вместо этого связана со шкалами A и B и охватывает углы примерно от 0,57 до 90 градусов; то, что следует ниже, необходимо соответствующим образом отрегулировать.) Шкала S имеет второй набор углов (иногда в разного цвета), которые идут в противоположном направлении и используются для косинусов. Касательные находятся путем сравнения шкалы T со шкалой C (или D) для углов менее 45 градусов. Для углов более 45 градусов используется шкала CI. Распространенные формы, такие как $k\sin x$ можно прочитать непосредственно от x по шкале S до результата по шкале D, когда индекс шкалы C установлен на k . Для углов менее 5,7 градуса синусы, тангенсы и радианы примерно равны и находятся по шкале ST или SRT (синусы, радианы и тангенсы) или просто делятся на 57,3 градуса/ радиан . Обратные тригонометрические функции находятся обратным процессом.

Многие логарифмические линейки имеют шкалы S, T и ST, отмеченные градусами и минутами (например, некоторые модели Keuffel и Esser (например, модели Doric Duplex 5 дюймов), последние модели правил типа Teledyne-Post Mannheim). Так называемый децитриг Вместо этого в моделях используются десятичные доли градусов.

Логарифмы и экспоненты [ править ]

Логарифмы и экспоненты по основанию 10 находятся с использованием линейной шкалы L. Некоторые логарифмические линейки имеют шкалу Ln, которая соответствует основанию e. Логарифмы по любому другому основанию можно вычислить, обратив процедуру вычисления степеней числа. Например, значения log2 можно определить, выровняв крайнюю левую или крайнюю правую цифру 1 на шкале C с цифрой 2 на шкале LL2, найдя число, логарифм которого необходимо вычислить, на соответствующей шкале LL и считав значение log2 на шкале C. шкала.

Сложение и вычитание [ править ]

Сложение и вычитание обычно не выполняются на логарифмических линейках, но возможно с использованием любого из следующих двух методов: ^[8]

Преобразование сложения и вычитания в деление (требуется для C и D или сопоставимых шкал):
- Использует тот факт , что частное двух переменных плюс (или минус) один раз на делитель равно их сумме (или разнице): ${\begin{aligned}\left({\frac {x}{y}}+1\right)y&=x+y\,{\text{ (addition)}},\\\left({\frac {x}{y}}-1\right)y&=x-y\,{\text{ (subtraction)}}.\end{aligned}}$
- Это похоже на технику сложения/вычитания, используемую для высокоскоростных электронных схем с логарифмической системой счисления в специализированных компьютерных приложениях, таких как суперкомпьютер Gravity Pipe (GRAPE) и скрытые модели Маркова .
Использование линейной шкалы L (доступно на некоторых моделях):
- После перемещения курсора вправо (для сложения) или влево (для вычитания) и возврата ползунка в 0, результат можно прочитать.

Обобщения [ править ]

Используя (почти) любые строго монотонные шкалы , можно производить и другие расчеты одним движением. ^[9]^[10] Например, обратные шкалы можно использовать для равенства ${\frac {1}{x}}+{\frac {1}{y}}={\frac {1}{z}}$ (расчет параллельных сопротивлений , среднего гармонического значения и т. д.), а для решения можно использовать квадратичные шкалы. $x^{2}+y^{2}=z^{2}$ .

Физический дизайн [ править ]

Стандартные линейные правила [ править ]

Ширина логарифмической линейки указана исходя из номинальной ширины весов. Шкала на наиболее распространенных «10-дюймовых» моделях на самом деле составляет 25 см, поскольку они были изготовлены в соответствии с метрическими стандартами, хотя некоторые правила предлагают слегка расширенные шкалы, чтобы упростить манипуляции, когда результат выходит за пределы. Карманные правила обычно имеют размер 5 дюймов (12 см). Модели шириной в пару метров (ярдов) предназначались для подвешивания в классах в учебных целях. ^[11]

Обычно деления обозначают масштаб с точностью до двух значащих цифр , а пользователь оценивает третью цифру. Некоторые высококачественные логарифмические линейки имеют курсоры-лупы, благодаря которым маркировку легче увидеть. Такие курсоры могут эффективно удвоить точность показаний, позволяя использовать 10-дюймовую логарифмическую линейку так же хорошо, как и 20-дюймовую модель.

Были разработаны и другие удобства. Тригонометрические шкалы иногда имеют двойную маркировку, черную и красную, с дополнительными углами, так называемый «дармштадтский» стиль. Дуплексные логарифмические линейки часто дублируют некоторые шкалы на оборотной стороне. Шкалы часто «разделяются» для повышения точности. ^{[ нужны дальнейшие объяснения ]}

Круговые линейки [ править ]

Круглые логарифмы бывают двух основных типов: один с двумя курсорами, другой с бесплатным блюдом и одним курсором. Версии с двумя курсорами выполняют умножение и деление, удерживая постоянный угол между курсорами при их вращении вокруг циферблата. Версия с одним курсором больше похожа на стандартную логарифмическую линейку за счет соответствующего выравнивания шкал.

Основное преимущество круглой логарифмической линейки состоит в том, что самый широкий размер инструмента был уменьшен примерно в 3 раза (т.е. на π ). Например, круглая линейка диаметром 10 см (3,9 дюйма) будет иметь максимальную точность, примерно равную обычной логарифмической линейке диаметром 31,4 см (12,4 дюйма). Круглые логарифмические линейки также исключают вычисления «за пределами шкалы», поскольку шкалы были спроектированы так, чтобы «обтекать»; их никогда не придется переориентировать, если результаты близки к 1,0 — правило всегда соответствует масштабу. Однако для нециклических неспиральных шкал, таких как S, T и LL, ширина шкалы сужается, чтобы освободить место для конечных полей. ^[12]

Круглые логарифмы механически более прочные и более плавные в движении, но точность выравнивания их шкалы чувствительна к центрированию центральной оси; смещение оси шарнира на 0,1 мм (0,0039 дюйма) в минуту может привести к ошибке выравнивания в худшем случае на 0,2 мм (0,0079 дюйма). Поворот предотвращает появление царапин на лице и курсорах. На внешних кольцах размещены шкалы высочайшей точности. Вместо «разделенных» шкал в высокопроизводительных круговых линейках используются спиральные шкалы для более сложных операций, таких как логарифмические шкалы. Одна восьмидюймовая круговая линейка премиум-класса имела 50-дюймовую спиральную бревенчатую шкалу. Примерно в 1970 году недорогая модель от BC Boykin (модель 510) имела 20 весов, включая 50-дюймовые весы CD (умножение) и логарифмические весы. RotaRule оснащен фрикционным тормозом курсора.

Основными недостатками круглых логарифмических линеек являются сложность расположения фигур вдоль блюда и ограниченное количество весов. Еще одним недостатком круглых логарифмических линеек является то, что менее важные масштабы расположены ближе к центру и имеют меньшую точность. Большинство учащихся освоили использование логарифмических линеек на линейных логарифмических линейках и не нашли причин для их переключения.

Одна логарифмическая линейка, которая до сих пор используется ежедневно во всем мире, — это E6B . Это круговая логарифмическая линейка, впервые созданная в 1930-х годах для пилотов самолетов, помогающая вести расчет . С помощью шкал, напечатанных на раме, он также помогает решать такие разные задачи, как преобразование значений времени, расстояния, скорости и температуры, ошибки компаса и расчет расхода топлива. Так называемое «молитвенное колесо» до сих пор продается в летных мастерских и по-прежнему широко используется. В то время как GPS сократил использование точного счисления для аэронавигации, а портативные калькуляторы взяли на себя многие из его функций, E6B по-прежнему широко используется в качестве основного или резервного устройства, и большинство летных школ требуют, чтобы их ученики имели определенную степень квалификации. в его использовании.

Колеса пропорций — это простые круговые линейки, используемые в графическом дизайне для расчета пропорций . Если выровнять исходные и желаемые значения размеров на внутреннем и внешнем колесах, их соотношение отобразится в процентах в небольшом окне. Хотя они и не так распространены с момента появления компьютерной верстки, их все еще производят и используют. ^{[ нужна ссылка ]}

В 1952 году швейцарская часовая компания Breitling представила наручные часы для пилотов со встроенной круглой логарифмической линейкой, предназначенной для расчетов полета: Breitling Navitimer . Круговое правило Navitimer, названное Breitling «навигационным компьютером», включало воздушную скорость , скорость /время набора высоты/снижения, время полета, расстояние и функции расхода топлива, а также километры – морские мили и галлоны – литры количества топлива. функции преобразования.

Простая круглая логарифмическая линейка производства Concision Co., Ltd., Токио, Япония, имеющая только инверсную, квадратную и кубическую шкалу. На реверсе находится удобный список из 38 метрических / британских коэффициентов пересчета.
Русская круглая логарифмическая линейка, похожая на карманные часы, которая работает как логарифмическая линейка с одним курсором, поскольку две иглы соединены вместе.
Двухшкальная логарифмическая линейка, встроенная в кольцо
Круглая логарифмическая линейка Пикетта с двумя курсорами. (ширина 4,25 дюйма/10,9 см). На реверсе имеется дополнительная шкала и один курсор.
Наручные часы Breitling Navitimer с круглой логарифмической линейкой
Передняя сторона Boykin RotaRule Model 510.
Задняя сторона Boykin RotaRule Model 510.
Карманный калькулятор Sperry 4016

Цилиндрические логарифмы [ править ]

Существует два основных типа цилиндрических логарифмических линеек: со спиральными шкалами, например, калькулятор Фуллера , Отиса Кинга и логарифмическая линейка Бигрейва , и с полосками, например, Thacher и некоторые модели Loga. В любом случае преимуществом является гораздо больший масштаб и, следовательно, потенциально более высокая точность, чем при использовании прямой или круговой линейки.

Калькулятор Фуллера, 1928 год.
Отис Кинг Модель К
Логарифмическая линейка Бигрейва
Логарифмическая линейка Тэчера, c. 1890 г.

Материалы [ править ]

Традиционно логарифмические линейки делались из твердых пород дерева, таких как красное дерево или самшит, с курсорами из стекла и металла. По крайней мере один высокоточный инструмент был изготовлен из стали.

В 1895 году японская фирма Hemmi начала изготавливать логарифмические линейки из бамбука, покрытого целлулоидом , который обладал преимуществами стабильности размеров, прочности и естественной самосмазки. Эти бамбуковые логарифмические линейки были представлены в Швеции в сентябре 1933 года. ^[13] и, вероятно, лишь немного раньше в Германии.

Весы также изготавливались из целлулоида или других полимеров или печатались на алюминии. Позже курсоры отливали из акрила или поликарбоната , иногда с тефлоновыми несущими поверхностями.

На всех логарифмических линейках премиум-класса цифры и шкалы были глубоко выгравированы, а затем заполнены краской или другой смолой . Окрашенные или отпечатанные логарифмические линейки считались некачественными, поскольку маркировка могла стереться или быть химически повреждена. Тем не менее, Пикетт, американская компания по производству логарифмических линеек, производила только печатные линейки. Линейки премиум-класса включали в себя умные механические защелки, чтобы линейка случайно не развалилась, и бортики, защищающие весы и курсор от трения о столешницы.

История [ править ]

Уильям Отред (1575–1660), изобретатель логарифмической линейки.

1763 г., иллюстрация логарифмической линейки

Логарифмическая линейка была изобретена примерно в 1620–1630 годах, вскоре после публикации Джоном Непером понятия логарифма . В 1620 году Эдмунд Гюнтер из Оксфорда разработал счетное устройство с единой логарифмической шкалой; с помощью дополнительных измерительных инструментов его можно было использовать для умножения и деления. ^[14] В ц. В 1622 году Уильям Отред из Кембриджа объединил две портативные линейки Гюнтера, чтобы создать устройство, которое можно узнать как современную логарифмическую линейку. ^[15] Отред оказался вовлеченным в резкий спор по поводу приоритета со своим бывшим учеником Ричардом Деламеном и предыдущими претензиями Вингейта. Идеи Отреда были обнародованы только в публикациях его ученика Уильяма Форстера в 1632 и 1653 годах.

В 1677 году Генри Коггешолл создал складную линейку длиной два фута для измерения древесины, названную логарифмической линейкой Коггешхолла , расширив использование логарифмической линейки за пределы математических исследований.

В 1722 году Уорнер ввел двух- и трехдекадную шкалу, а в 1755 году Эверард включил перевернутую шкалу; логарифмическая линейка, содержащая все эти шкалы, обычно известна как «многофазное» правило.

В 1815 году Питер Марк Роже изобрел логарифмическую линейку, которая включала в себя шкалу, отображающую логарифм логарифма. Это позволило пользователю напрямую выполнять вычисления с использованием корней и показателей степени. Это было особенно полезно для дробных полномочий.

В 1821 году Натаниэль Боудич описал в « Американском практическом навигаторе» «скользящую линейку», которая содержала масштабированные тригонометрические функции на фиксированной части и линию лог-синусов и лог-тангенсов на ползунке, используемом для решения навигационных задач.

В 1845 году Пол Кэмерон из Глазго представил морскую логарифмическую линейку, способную отвечать на навигационные вопросы, включая прямое восхождение и склонение Солнца и главных звезд. ^[16]

Современная форма [ править ]

Инженер использует логарифмическую линейку на фоне механического калькулятора, середина 20 века.

Более современная форма логарифмической линейки была создана в 1859 году лейтенантом французской артиллерии Амеде Мангеймом , которому повезло как в том, что его линейка была изготовлена фирмой с национальной репутацией, так и в том, что она была принята французской артиллерией. Правило Мангейма претерпело две основные модификации, которые упростили его использование по сравнению с предыдущими логарифмическими линейками общего назначения. Такие правила имели четыре основные шкалы: A, B, C и D, и D была единственной десятичной логарифмической шкалой; У C было две декады, как у A и B. Большинство операций выполнялось в масштабах A и B; D использовался только для поиска квадратов и квадратных корней.

Мангейм изменил шкалу C на однодекадную шкалу и выполнил большинство операций с C и D вместо A и B. Поскольку шкалы C и D были однодекадными, их можно было читать более точно, поэтому результаты правила могли быть более точными. точный. Это изменение также облегчило включение квадратов и квадратных корней в более крупные вычисления. В отличие от почти всех предыдущих правил в правиле Мангейма также был курсор, поэтому любой масштаб можно было легко и точно сравнивать по ширине правила. «Правило Мангейма» стало стандартным устройством логарифмической линейки в конце 19 века и оставалось общим стандартом на протяжении всей эпохи логарифмической линейки.

Рост инженерной профессии в конце 19 века привел к широкому использованию логарифмической линейки, начиная с Европы и в конечном итоге приживаясь и в Соединенных Штатах. Правило дуплекса было изобретено Уильямом Коксом в 1891 году и произведено компанией Keuffel and Esser Co. из Нью-Йорка. ^[17]^[18]

В 1881 году американский изобретатель Эдвин Тэчер представил свою цилиндрическую линейку, которая имела гораздо более длинный масштаб, чем стандартные линейные линейки, и, таким образом, могла производить вычисления с более высокой точностью, примерно от четырех до пяти значащих цифр. Однако линейка Тэчера была довольно дорогой и непереносимой, поэтому ее использовали в гораздо более ограниченном количестве, чем обычные логарифмические линейки.

Астрономические работы также требовали точных вычислений, и в Германии XIX века в одной обсерватории использовалась стальная логарифмическая линейка длиной около двух метров. К нему был прикреплен микроскоп, что обеспечивало точность до шести знаков после запятой. ^{[ нужна ссылка ]}

В 1920-е годы писатель и инженер Невил Шут Норвегий (он назвал свою автобиографию «Линейкой скольжения» ) был главным расчетчиком при проектировании британского дирижабля R100 для компании Vickers Ltd. с 1924 года. Расчеты напряжений для каждой поперечной рамы требовали вычислений с помощью пары калькуляторы (люди), использующие цилиндрические логарифмические линейки Фуллера в течение двух-трех месяцев. Одновременное уравнение содержало до семи неизвестных величин, на его решение уходило около недели, и его приходилось повторять с другим набором провисающих проводов, если предположение о том, какой из восьми радиальных проводов провисает, было неверным и один из проводов угадал быть слабым не было слабым. После нескольких месяцев работы над заполнением примерно пятидесяти листов с расчетами «истина была раскрыта (и) принесла удовлетворение, почти равное религиозному опыту». ^[19]

В 1937 году физик Люси Хейнер спроектировала и сконструировала круглую логарифмическую линейку шрифтом Брайля . ^[20]

На протяжении 1950-х и 1960-х годов логарифмическая линейка была символом профессии инженера, точно так же, как стетоскоп является символом профессии врача. ^[21]

Алюминиевые логарифмические линейки марки Pickett использовались в проекта «Аполлон» космических миссиях . Модель N600-ES, принадлежавшая Баззу Олдрину , летавшая с ним на Луну на «Аполлоне-11», была продана на аукционе в 2007 году. ^[22] Модель N600-ES, взятая с собой на «Аполлон-13» в 1970 году, принадлежит Национальному музею авиации и космонавтики . ^[23]

Некоторые студенты-инженеры и инженеры носили десятидюймовые логарифмические линейки в кобуре на поясе, что было обычным явлением в кампусах даже в середине 1970-х годов. До появления карманного цифрового калькулятора учащиеся также могли использовать правило десяти или двадцати дюймов для точной работы дома или в офисе. ^[24] нося с собой пятидюймовую карманную логарифмическую линейку.

В 2004 году исследователи образования Дэвид Б. Шер и Дин К. Натаро разработали новый тип логарифмической линейки, основанный на простафаерезисе — алгоритме быстрого вычисления продуктов, который предшествует логарифмам. Однако практического интереса к созданию такого самолета, кроме первоначального прототипа, не было. ^[25]

Специализированные калькуляторы [ править ]

Логарифмические линейки часто в той или иной степени специализированы для области их использования, например, акциз, расчет доказательств, инженерия, навигация и т. Д., А некоторые логарифмические линейки чрезвычайно специализированы для очень узких применений. Например, в каталоге John Rabone & Sons 1892 года указана «Измерительная лента и измеритель для крупного рогатого скота», устройство для оценки веса коровы на основе ее измерений.

Существовало множество специализированных логарифмических линеек для фотографических приложений. Например, актинограф Хертера и Дриффилда представлял собой двухкамерное устройство из самшита, латуни и картона для оценки экспозиции в зависимости от времени суток, времени года и широты.

Специализированные логарифмические линейки были изобретены для различных видов техники, бизнеса и банковского дела. Часто они имели общие расчеты, непосредственно выраженные в виде специальных шкал, например расчеты кредита, оптимальные объемы закупок или конкретные инженерные уравнения. Например, компания Fisher Controls распространила специальную логарифмическую линейку, адаптированную для решения уравнений, используемых для выбора подходящего размера промышленных клапанов регулирования расхода. ^[26]

Линейки с пилотным шаром использовались метеорологами в метеорологических службах для определения скорости ветра на высотах от поднимающегося пилотного шара, наполненного водородом или гелием. ^[27]

E6 -B — это круглая логарифмическая линейка, используемая пилотами и штурманами.

Круглые логарифмы для оценки дат овуляции и фертильности известны как колесные калькуляторы . ^[28]

Публикация Министерства обороны 1962 года. ^[29] позорно включал в себя специальную круглую логарифмическую линейку для расчета последствий взрыва, избыточного давления и радиационного воздействия при заданной мощности атомной бомбы. ^[30]

Авиационный компьютер E6-B
Датчик для скота John Rabone & Sons 1892 г.
и Дриффилда Актинограф Хертера
Криптографическая логарифмическая линейка, использовавшаяся швейцарской армией между 1914 и 1940 годами.
Редкий дробный сумматор

Отклонить [ править ]

Важность логарифмической линейки начала уменьшаться по мере того, как электронные компьютеры, новый, но редкий ресурс 1950-х годов, стали более доступными для технических работников в 1960-е годы.

Первым шагом к отказу от логарифмических линеек стало появление относительно недорогих электронных настольных научных калькуляторов. В их число входили Wang Laboratories LOCI-2, ^[31]^[32] введенный в 1965 году, в котором для умножения и деления использовались логарифмы; и Hewlett-Packard HP 9100A , представленный в 1968 году. ^[33] Оба они были программируемыми и обеспечивали экспоненциальные и логарифмические функции; HP имела тригонометрические функции (синус, косинус и тангенс), а также гиперболические тригонометрические функции. HP использовала алгоритм CORDIC (цифровой компьютер вращения координат). ^[34] который позволяет вычислять тригонометрические функции, используя только операции сдвига и сложения. Этот метод облегчил разработку научных калькуляторов все меньшего размера.

Как и в случае с мейнфреймами, доступность этих настольных компьютеров существенно не повлияла на повсеместное использование логарифмической линейки, пока в середине 1970-х годов не стали доступны дешевые ручные научные электронные калькуляторы, после чего их популярность быстро пришла в упадок. Карманный научный калькулятор Hewlett-Packard HP-35 был первым портативным устройством такого типа, но в 1972 году он стоил 395 долларов США. Это было оправдано для некоторых инженеров, но слишком дорого для большинства студентов.

Примерно в 1974 году недорогие портативные электронные научные калькуляторы начали делать логарифмические линейки в значительной степени устаревшими. ^[35]^[36]^[37]^[38] К 1975 году базовые электронные калькуляторы с четырьмя функциями можно было купить менее чем за 50 долларов, а к 1976 году научный калькулятор TI-30 продавался менее чем за 25 долларов (134 доллара с учетом инфляции).

1980 год стал последним годом соревнований Университетской межшкольной лиги (UIL) в Техасе по использованию логарифмических линеек. ^{[ нужна ссылка ]} Первоначально UIL был организован в 1910 году для проведения литературных мероприятий. ^{[ нужна ссылка ]} но также стал руководящим органом школьных спортивных мероприятий.

с электронными цифровыми Сравнение калькуляторами

Даже в период своего расцвета логарифмические линейки так и не завоевали популярность у широкой публики. ^[39] Сложение и вычитание не являются хорошо поддерживаемыми операциями на логарифмических линейках, и выполнение вычислений на логарифмической линейке обычно происходит медленнее, чем на калькуляторе. ^[40] Это побудило инженеров использовать математические уравнения, которые отдавали предпочтение операциям, простым в использовании логарифмической линейки, а не более точным, но сложным функциям; эти приближения могут привести к неточностям и ошибкам. ^[41] С другой стороны, пространственное ручное управление логарифмическими линейками развивает у пользователя интуицию числовых отношений и масштаба, которой часто не хватает людям, которые использовали только цифровые калькуляторы. ^[42] Логарифмическая линейка также будет отображать все условия расчета вместе с результатом, что устраняет неопределенность относительно того, какой расчет был фактически выполнен. Таким образом, ее сравнивают с обратной польской записью (RPN), реализованной в электронных калькуляторах. ^[43]

Логарифмическая линейка требует от пользователя отдельно вычислить порядок величины ответа, чтобы расположить десятичную точку в результатах. Например, 1,5 × 30 (что равно 45) покажет тот же результат, что и 1 500 000 × 0,03 (что равно 45 000 ). Этот отдельный расчет заставляет пользователя отслеживать величину в кратковременной памяти (которая подвержена ошибкам), вести записи (что обременительно) или рассуждать о ней на каждом этапе (что отвлекает от других требований расчета).

Типичная арифметическая точность логарифмической линейки составляет около трёх значащих цифр по сравнению со многими цифрами на цифровых калькуляторах. Поскольку порядок величины приобретает наибольшее значение при использовании логарифмической линейки, пользователи с меньшей вероятностью совершают ошибки ложной точности .

При выполнении последовательности умножения или деления на одно и то же число ответ часто можно определить, просто взглянув на логарифмическую линейку, без каких-либо манипуляций. Это может быть особенно полезно при расчете процентов (например, для результатов тестов) или при сравнении цен (например, в долларах за килограмм). Несколько расчетов скорости, времени и расстояния можно выполнить без помощи рук с помощью логарифмической линейки. Другие полезные линейные преобразования, такие как фунты в килограммы, можно легко отметить на правиле и использовать непосредственно в расчетах.

Будучи полностью механической, логарифмическая линейка не зависит от электроэнергии в сети или батарей. Механическая неточность в логарифмических линейках, которые были плохо сконструированы или деформированы под воздействием тепла или использования, приведет к ошибкам.

Многие моряки хранят логарифмы в качестве запасного варианта для навигации на случай сбоя в электросети или разрядки аккумулятора на длинных участках маршрута. Логарифмические линейки до сих пор широко используются в авиации, особенно для небольших самолетов. На смену им приходят только интегрированные, специализированные и дорогие борткомпьютеры, а не универсальные калькуляторы. Круглая логарифмическая линейка E6B , используемая пилотами, находится в непрерывном производстве и по-прежнему доступна в различных моделях. Некоторые наручные часы, предназначенные для использования в авиации, до сих пор имеют шкалу логарифмической линейки, позволяющую осуществлять быстрые расчеты. Двумя яркими примерами являются Citizen Skyhawk AT и Seiko Flightmaster SNA411. ^[44]

использование Современное

Даже в XXI веке некоторые люди предпочитают логарифмическую линейку электронному калькулятору как практичному вычислительному устройству. Другие хранят свои старые логарифмические линейки из чувства ностальгии или коллекционируют их в качестве хобби. ^[45]

Популярной коллекционной моделью является Keuffel & Esser Deci-Lon , научно-техническая логарифмическая линейка премиум-класса, доступная как в десятидюймовой (25 см) «обычной» ( Deci-Lon 10 ), так и в пятидюймовой «карманной» ( Deci) -Лон 5 ) вариант. Еще одна ценная американская модель — восьмидюймовая (20 см) круговая линейка Scientific Instruments. Из европейских правил Faber-Castell модели высокого класса пользуются наибольшей популярностью среди коллекционеров.

Хотя на рынке имеется множество логарифмических линеек, экземпляры в хорошем состоянии, как правило, стоят дорого. Многие правила, выставленные на продажу на интернет-аукционах, повреждены или в них отсутствуют детали, и продавец может не знать достаточно, чтобы предоставить соответствующую информацию. Запасные части редки, дороги и обычно доступны только для отдельной покупки на веб-сайтах отдельных коллекционеров. Правила Койфеля и Эссера, существовавшие примерно до 1950 года, особенно проблематичны, поскольку наконечники курсоров, сделанные из целлулоида , имеют тенденцию со временем химически разрушаться. Методы консервации пластика можно использовать для замедления износа некоторых старых логарифмических линеек, а 3D-печать можно использовать для воссоздания недостающих или безвозвратно сломанных частей курсора. ^[46]

Есть еще несколько источников совершенно новых логарифмических линеек. Токийская компания Concision, начавшая свою деятельность с производства круглых логарифмических линеек в июле 1954 года, ^[47] продолжает производить и продавать их сегодня. В сентябре 2009 года интернет-магазин ThinkGeek представил свою собственную марку прямых логарифмических линеек, описанную как «точные копии», «изготовленные индивидуально вручную». ^[48] В 2012 году их больше не было. ^[49] Кроме того, до середины 2018 года у Faber-Castell в наличии было несколько логарифмических линеек, которые можно было приобрести за рубежом через их интернет-магазин. ^[50] Пропорциональные колеса до сих пор используются в графическом дизайне.

Для смартфонов и планшетов на базе Android и iOS доступны различные приложения-симуляторы логарифмических линеек.

Специализированные логарифмы, такие как E6B, используемые в авиации, и артиллерийские логарифмы, используемые при наводке артиллерии, все еще используются, хотя и уже не на регулярной основе. Эти правила используются как часть процесса преподавания и обучения, поскольку, обучаясь их использованию, учащийся также узнает о принципах, лежащих в основе расчетов, а также позволяет учащемуся использовать эти инструменты в качестве резервной копии на случай, если современные электроника в обычном использовании выходит из строя.

Коллекции [ править ]

В Музее Массачусетского технологического института в Кембридже, штат Массачусетс , хранится коллекция из сотен логарифмических линеек, номограмм и механических калькуляторов . ^[51] Коллекция компании Keuffel and Esser от производителя логарифмических линеек, ранее находившегося в Хобокене, штат Нью-Джерси , была передана в дар Массачусетскому технологическому институту примерно в 2005 году, что существенно расширило существующие запасы. ^[52] Избранные предметы из коллекции обычно выставлены в музее. ^[53]^[54]

Международный музей логарифмических линеек считается «самым обширным в мире ресурсом по всему, что касается логарифмических линеек и логарифмических калькуляторов». ^[55] На веб-странице музея в разделе «Библиотека логарифмических линеек» представлена обширная литература по логарифмическим линейкам. ^[56]

См. также [ править ]

Абакус – инструмент для расчета
Компьютер (профессия) - человек, выполняющий математические расчеты до того, как стали доступны электронные компьютеры.
Бортовой компьютер - круглая логарифмическая линейка, используемая в авиации.
С плавающей запятой — компьютерная аппроксимация действительных чисел
Ганс Питер Лун – американский учёный-компьютерщик
Номограмма – Аналоговый графический калькулятор
Сектор (инструмент) – Математический инструмент, состоящий из двух шарнирных линеек.
Слайд-калькулятор – Механический калькулятор
Слайд-диаграмма – портативное устройство с движущимися частями, обычно бумажное, обычно распечатываемое для справки или вычислений.
Хронология вычислений
Шкала нониуса - вспомогательная шкала измерительного устройства, используемая для повышения точности.
Volvelle - бумажная конструкция с вращающимися частями, может считаться подклассом слайд-диаграммы или подвижной книги.

Ссылки [ править ]

^ Роджер Р. Флинн (июнь 2002 г.). Компьютерные науки . Том. 1. Макмиллан. п. 175. ИСБН 978-0-02-865567-3 . Проверено 30 марта 2013 г. Логарифмическая линейка является примером механического аналогового компьютера...
^ Эрнст Блейлер; Роберт Озиас Хаксби (21 сентября 2011 г.). Электронные методы . Академическая пресса. п. 638. ИСБН 978-0-08-085975-0 . Проверено 30 марта 2013 г. Например, логарифмические линейки представляют собой механические аналоговые компьютеры.
^ «Правила слайдов» . Музей МТИ . Массачусетский технологический институт . Проверено 1 мая 2019 г.
^ Берри, Лестер В.; ван ден Барк, Мелвин (1953). Американский тезаурус сленга: полный справочник разговорной речи (2-е изд.). Кроуэлл. OCLC 319462 .
^ Петроски, Генри (2011). Азбука инженера: крупицы более мягкой стороны профессии . Издательство Кембриджского университета. стр. 46–47. ISBN 9781139505307 . Проверено 21 марта 2017 г.
^ Маркотт, доктор философии, Эрик (2002). «Типы логарифмических линеек Эрика и их масштабы» . www.sliderule.ca . Проверено 13 июля 2021 г.
^ «инструкция по эксплуатации» . сфера.bc.ca . стр. 7–8. Архивировано из оригинала 2 апреля 2007 г. Проверено 14 марта 2007 г.
^ «Антикварк: хитрости с логарифмической линейкой» . antiquark.com .
^ Иштван, Салкай (2016). «Общие функции с двумя переменными на логарифмической линейке» . Журнал Общества Отцов . 27 (1): 14–18. arXiv : 1612.03955 . Бибкод : 2016arXiv161203955S .
^ Иштван, Салкай (2016). «Общие функции с двумя переменными на логарифмической линейке». arXiv : 1612.03955 [ math.HO ].
^ «Правила слайдов» . Tbullock.com. 08.12.2009. Архивировано из оригинала 3 февраля 2013 г. Проверено 20 февраля 2010 г.
^ По крайней мере, одно круговое правило, модель Гилсона 1931 года, пожертвовало некоторыми шкалами, обычно встречающимися в логарифмических линейках, чтобы получить дополнительное разрешение при умножении и делении. Он функционировал за счет использования спиральной шкалы C, длина которой, как утверждалось, составляла 50 футов и допускала считывание до пяти значащих цифр. См. http://www.sphere.bc.ca/test/gilson/gilson-manual2.jpg. Архивировано 30 декабря 2006 г. в Wayback Machine . Фото можно увидеть на http://www.hpmuseum.org/srcirc.htm . Руководство по эксплуатации устройства, продаваемого Dietzgen, можно найти по адресу http://www.sliderulemuseum.com/SR_Library_General.htm. Архивировано 14 февраля 2007 г. в Wayback Machine . Все получены 14 марта 2007 г.
^ «336 (Технический журнал / 1933. Общий отдел)» . Рунеберг.орг . Проверено 20 февраля 2010 г.
^ Смит, Дэвид Э. (1958). История математики . Курьерская корпорация. п. 205. ИСБН 9780486204307 .
^ Эпплбаум, Уилбур (16 декабря 2003 г.). «Линейка» . Энциклопедия научной революции: от Коперника до Ньютона . Рутледж. Бибкод : 2000esrc.book.....A . ISBN 9781135582555 .
^ «Морская логарифмическая линейка Кэмерона», Журнал практического механика и инженера , апрель 1845 г., стр. 187 и фото XX-B.
^ Келлс, Лайман М.; Керн, Уиллис Ф.; Бланд, Джеймс Р. (1943). Логарифмическая линейка Log-Log Duplex Decitrig № 4081: Руководство . Койфель и Эссер. п. 92. Архивировано из оригинала 14 февраля 2009 г.
^ Логарифмическая линейка многофазного дуплекса, Самоучитель , Брекенридж, 1922, с. 20.
^ Норвегия, Невил Шют (1954). Слайд-правило . Лондон: Уильям Хайнеманн. стр. 76–78.
^ Ведьмак, CM (1 декабря 1954 г.). «Физика без зрения» . Физика сегодня . 7 (12): 8–10. дои : 10.1063/1.3061483 . ISSN 0031-9228 .
^ Столл, Клифф (2006). «Когда правили правила слайдов» . Научный американец . 294 (5): 80–87. Бибкод : 2006SciAm.294e..80S . doi : 10.1038/scientificamerican0506-80 . ISSN 0036-8733 . JSTOR 26061456 . ПМИД 16708492 .
^ «Лот 25368 Логарифмическая линейка Базза Олдрина с Аполлона-11 – полет на Луну. ... Большой форматный авиационно-космический аукцион № 669, сентябрь 2007 г.» . Аукционы наследия. Архивировано из оригинала 3 сентября 2013 г. Проверено 3 сентября 2013 г.
^ «Счетная линейка, 5 дюймов, Pickett N600-ES, Apollo 13» . Смитсоновский национальный музей авиации и космонавтики. Архивировано из оригинала 9 октября 2013 г. Проверено 3 сентября 2013 г.
^ Чарльз Овертон Харрис, Упрощенная логарифмическая линейка , Американское техническое общество, 1961, стр. 5.
^ Шер, Дэвид Б.; Натаро, Дин К. (2 июня 2009 г.). «Простафаэретическая логарифмическая линейка: механическое устройство умножения, основанное на тригонометрических тождествах» . Математика и компьютерное образование, Vol. 38, вып. 1 (зима 2004 г.): 37–43 . Архивировано из оригинала 10 мая 2005 г. Проверено 20 февраля 2010 г. - через Findarticles.com.
^ «Правила калибровки Фишера» . natgasedu.com . Архивировано из оригинала 6 января 2010 г. Проверено 6 октября 2009 г.
^ «Правила полета пилотного воздушного шара» . www.pilotballoon.com . Архивировано из оригинала 28 сентября 2016 г. Проверено 28 сентября 2016 г.
^ Росс, МГ (2003). «Круг времени: ошибки в использовании колеса для беременных». Журнал медицины матери, плода и новорожденных . 14 (6): 370–372. дои : 10.1080/14767050412331312200 . ПМИД 15061314 . S2CID 20101166 .
^ «Последствия ядерного оружия» . Проверено 2 мая 2021 г.
^ «Линейка Стрейнджлав» . Проверено 2 мая 2021 г.
^ «Ван LOCI-2» . oldcalculatormuseum.com .
^ Ван Лаборатории (декабрь 1966 г.). «Теперь вы можете за несколько минут определить состав сополимера, сидя за столом». Аналитическая химия . 38 (13): 62А–63А. дои : 10.1021/ac50155a005 .
^ Лейбсон, Стивен (2010). «Проект HP 9100: экзотермическая реакция» . Проверено 2 января 2016 г. ^{[ постоянная мертвая ссылка ]}
^ Волдер, Джек Э. (июнь 2000 г.). «Рождение CORDIC» (PDF) . Журнал обработки сигналов СБИС . 25 (2): 101–105. дои : 10.1023/а:1008110704586 . ISSN 0922-5773 . S2CID 112881 . Архивировано из оригинала (PDF) 4 марта 2016 г. Проверено 2 января 2016 г.
^ Беренс, Лоуренс; Розен, Леонард Дж. (1982). Письмо и чтение по учебной программе . Маленький, Браун . п. 273. Затем, всего десять лет назад, изобретение карманного калькулятора почти в мгновение ока сделало логарифмическую линейку устаревшей...
^ Маор, Эли (2009). е: История числа . Издательство Принстонского университета. п. 16. ISBN 978-0-691-14134-3 . Затем, в начале 1970-х годов, на рынке появились первые электронные ручные калькуляторы, и через десять лет логарифмическая линейка устарела.
^ Каслден, Родни (2007). Изобретения, изменившие мир . Футура. п. 157. ИСБН 978-0-7088-0786-6 . С изобретением калькулятора логарифмическая линейка мгновенно устарела.
^ Деннинг, Питер Дж .; Меткалф, Роберт М. (1998). За пределами вычислений: следующие пятьдесят лет вычислений . Спрингер . п. xiv. ISBN 978-0-387-98588-6 . Первый ручной калькулятор появился в 1972 году и в одночасье сделал логарифмическую линейку устаревшей.
^ Столл, Клифф. «Когда правили правила слайдов», Scientific American, май 2006 г., стр. 80–87 . «Трудность обучения пользованию логарифмическими линейками препятствовала их использованию среди простого народа . Да, случайный менеджер продуктового магазина рассчитывал скидки на палочке, и этот автор однажды поймал своего школьного учителя английского языка, подсчитывающего статистику для победителей тройных скачек на беговой дорожке. Но линейки так и не вошли в повседневную жизнь, потому что с их помощью нельзя было выполнять простое сложение и вычитание, не говоря уже о сложности отслеживания десятичной точки, которые оставались инструментами для технарей».
^ Уотсон, Джордж Х. «Проблемное обучение и три буквы технологии», Сила проблемного обучения , Барбара Дач, Сьюзан Гро, Дебора Аллен, ред., Stylus Publishing, LLC, 2001. «Численные вычисления в физика и химия для первокурсников были мучительными; однако, похоже, это не касалось тех студентов, которым посчастливилось уже иметь калькулятор. Я хорошо помню, что в конце 1974 года студентам, которые все еще пользовались логарифмическими линейками, давали дополнительные. 15 минут на выпускной экзамен, чтобы компенсировать вычислительное преимущество, обеспечиваемое калькулятором, — едва ли адекватная компенсация, по мнению остальных практикующих логарифмических линеек».
^ Столл, Клифф. «Когда правили правила слайдов», Scientific American, май 2006 г., стр. 80–87 . «Поскольку вычисления происходили буквально со скоростью руки и при этом не хватало точности, математики работали над упрощением сложных задач. Поскольку линейные уравнения были более дружелюбны к логарифмическим линейкам, чем более сложные функции, ученые изо всех сил пытались линеаризовать математические отношения, часто охватывая высшие порядки. или менее важные термины под ковром вычислений. Таким образом, конструктор автомобилей может рассчитывать расход топлива, глядя в основном на мощность двигателя, игнорируя при этом, как трение воздуха меняется в зависимости от скорости. экономия времени, понимание и понимание. С другой стороны, эти приближения могут скрыть ошибки и привести к грубым ошибкам».
^ Столл, Клифф. «Когда правили правила слайдов», Scientific American , май 2006 г., стр. 80–87 . «Одним из эффектов было то, что пользователи чувствовали себя близкими к цифрам, осознавая ошибки округления и систематические неточности, в отличие от пользователей сегодняшних программ компьютерного проектирования. Поговорите с инженером из 1950-х годов, и вы, скорее всего, услышите жалобы на те дни, когда расчеты шли рука об руку с более глубоким пониманием. Вместо того, чтобы вводить числа в компьютерную программу, инженер понимал тонкости нагрузок и напряжений, напряжений и токов, углов и расстояний. Числовые ответы, составленные вручную, означали проблему. решение посредством знаний и анализа, а не простого подсчета чисел».
^ Уильямс, Эл (21 июня 2023 г.). «Похвала RPN (с Python или C)» . Хакадей . Архивировано из оригинала 23 сентября 2023 г. Проверено 23 сентября 2023 г.
^ «Citizen Watch Company – Citizen Eco-Drive / США, Канада, Великобритания, ИрландияCitizen Watch» . Citizenwatch.com . Архивировано из оригинала 22 апреля 2014 г. Проверено 21 апреля 2014 г.
^ «Линейки Грега – ссылки на сборщиков логарифмических линеек» . Sliderule.ozmanor.com. 29 июля 2004 г. Проверено 20 февраля 2010 г.
^ «Восстановление и исправление правил слайдов и заметок» . Международный музей логарифмических линеек .
^ «О КОНЦЕНТРАЦИИ» . Краткий.co.jp. Архивировано из оригинала 12 марта 2012 г. Проверено 20 февраля 2010 г.
^ «Линейка» . ДумайГик. Архивировано из оригинала 27 марта 2010 г. Проверено 8 апреля 2015 г.
^ «Линейка» . ДумайГик. Архивировано из оригинала 15 апреля 2012 г. Проверено 8 апреля 2015 г.
^ «Рехеншибер» . Фабер-Кастелл. Архивировано из оригинала 21 ноября 2013 г. Проверено 17 января 2012 г. Считается, что у них все еще могут быть какие-то линейки, но на их новом веб-сайте и в интернет-магазине их нет.
^ «Категория общего собрания MIT «Коллекция логарифмических правил» .
^ «Музей MIT соответствует требованиям» . Новости МТИ . Массачусетский технологический институт. 11 января 2005 г. Проверено 1 мая 2019 г.
^ «Правила слайдов» . Музей МТИ . Массачусетский технологический институт. Архивировано из оригинала 01 мая 2019 г. Проверено 1 мая 2019 г.
^ «Музей MIT — Правила слайдов» . proundesign.com . Проун Дизайн. Архивировано из оригинала 01 мая 2019 г. Проверено 1 мая 2019 г.
^ Тернер, Кимберли (07 октября 2009 г.). «Линейка: 101». Газеты родного города Колорадо .
^ «Главный стол библиотеки логарифмических линеек» . Международный музей логарифмических линеек . Архивировано из оригинала 07 января 2023 г. Проверено 7 января 2023 г.

Внешние ссылки [ править ]

Международный музей логарифмических линеек
История, теория и использование инженерной логарифмической линейки . Доктор Джеймс Б. Калверт, Денверский университет.
Домашняя страница круга логарифмической линейки Соединенного Королевства. Архивировано 28 сентября 2015 г. на Wayback Machine.
Домашняя страница логарифмического общества Oughtred Society — посвящена сохранению и истории логарифмических линеек.
Правила слайдов Рода Ловетта - обширный сайт Aristo со множеством возможностей поиска.
Виртуальная галерея логарифмических правил Дерека — Javascript-моделирование исторических логарифмических правил.
«Линейка» . Новая международная энциклопедия . 1905.
«Линейка» . Американская энциклопедия . 1920.
Правила расчета — очень большая коллекция Фабера Кастелла.
Сборник логарифмических правил — French Slide Rules (Graphoplex, Tavernier-Gravet и другие)
Сайт логарифмической линейки Эрика — история и использование
Правила для слайдов — информация из Музея калькуляторов HP
Описания в алфавитном порядке по названиям брендов с изображениями (Vintage Tech. Assoc.)

[Flynn2002-1] Роджер Р. Флинн (июнь 2002 г.). Компьютерные науки . Том. 1. Макмиллан. п. 175. ИСБН 978-0-02-865567-3 . Проверено 30 марта 2013 г. Логарифмическая линейка является примером механического аналогового компьютера...

[BleulerHaxby2011-2] Эрнст Блейлер; Роберт Озиас Хаксби (21 сентября 2011 г.). Электронные методы . Академическая пресса. п. 638. ИСБН 978-0-08-085975-0 . Проверено 30 марта 2013 г. Например, логарифмические линейки представляют собой механические аналоговые компьютеры.

[MIT-Museum-3] «Правила слайдов» . Музей МТИ . Массачусетский технологический институт . Проверено 1 мая 2019 г.

[4] Берри, Лестер В.; ван ден Барк, Мелвин (1953). Американский тезаурус сленга: полный справочник разговорной речи (2-е изд.). Кроуэлл. OCLC 319462 .

[petroski-5] Петроски, Генри (2011). Азбука инженера: крупицы более мягкой стороны профессии . Издательство Кембриджского университета. стр. 46–47. ISBN 9781139505307 . Проверено 21 марта 2017 г.

[6] Маркотт, доктор философии, Эрик (2002). «Типы логарифмических линеек Эрика и их масштабы» . www.sliderule.ca . Проверено 13 июля 2021 г.

[7] «инструкция по эксплуатации» . сфера.bc.ca . стр. 7–8. Архивировано из оригинала 2 апреля 2007 г. Проверено 14 марта 2007 г.

[8] «Антикварк: хитрости с логарифмической линейкой» . antiquark.com .

[9] Иштван, Салкай (2016). «Общие функции с двумя переменными на логарифмической линейке» . Журнал Общества Отцов . 27 (1): 14–18. arXiv : 1612.03955 . Бибкод : 2016arXiv161203955S .

[10] Иштван, Салкай (2016). «Общие функции с двумя переменными на логарифмической линейке». arXiv : 1612.03955 [ math.HO ].

[11] «Правила слайдов» . Tbullock.com. 08.12.2009. Архивировано из оригинала 3 февраля 2013 г. Проверено 20 февраля 2010 г.

[12] По крайней мере, одно круговое правило, модель Гилсона 1931 года, пожертвовало некоторыми шкалами, обычно встречающимися в логарифмических линейках, чтобы получить дополнительное разрешение при умножении и делении. Он функционировал за счет использования спиральной шкалы C, длина которой, как утверждалось, составляла 50 футов и допускала считывание до пяти значащих цифр. См. http://www.sphere.bc.ca/test/gilson/gilson-manual2.jpg. Архивировано 30 декабря 2006 г. в Wayback Machine . Фото можно увидеть на http://www.hpmuseum.org/srcirc.htm . Руководство по эксплуатации устройства, продаваемого Dietzgen, можно найти по адресу http://www.sliderulemuseum.com/SR_Library_General.htm. Архивировано 14 февраля 2007 г. в Wayback Machine . Все получены 14 марта 2007 г.

[13] «336 (Технический журнал / 1933. Общий отдел)» . Рунеберг.орг . Проверено 20 февраля 2010 г.

[14] Смит, Дэвид Э. (1958). История математики . Курьерская корпорация. п. 205. ИСБН 9780486204307 .

[15] Эпплбаум, Уилбур (16 декабря 2003 г.). «Линейка» . Энциклопедия научной революции: от Коперника до Ньютона . Рутледж. Бибкод : 2000esrc.book.....A . ISBN 9781135582555 .

[16] «Морская логарифмическая линейка Кэмерона», Журнал практического механика и инженера , апрель 1845 г., стр. 187 и фото XX-B.

[fn_3-17] Келлс, Лайман М.; Керн, Уиллис Ф.; Бланд, Джеймс Р. (1943). Логарифмическая линейка Log-Log Duplex Decitrig № 4081: Руководство . Койфель и Эссер. п. 92. Архивировано из оригинала 14 февраля 2009 г.

[fn_4-18] Логарифмическая линейка многофазного дуплекса, Самоучитель , Брекенридж, 1922, с. 20.

[19] Норвегия, Невил Шют (1954). Слайд-правило . Лондон: Уильям Хайнеманн. стр. 76–78.

[20] Ведьмак, CM (1 декабря 1954 г.). «Физика без зрения» . Физика сегодня . 7 (12): 8–10. дои : 10.1063/1.3061483 . ISSN 0031-9228 .

[21] Столл, Клифф (2006). «Когда правили правила слайдов» . Научный американец . 294 (5): 80–87. Бибкод : 2006SciAm.294e..80S . doi : 10.1038/scientificamerican0506-80 . ISSN 0036-8733 . JSTOR 26061456 . ПМИД 16708492 .

[22] «Лот 25368 Логарифмическая линейка Базза Олдрина с Аполлона-11 – полет на Луну. ... Большой форматный авиационно-космический аукцион № 669, сентябрь 2007 г.» . Аукционы наследия. Архивировано из оригинала 3 сентября 2013 г. Проверено 3 сентября 2013 г.

[23] «Счетная линейка, 5 дюймов, Pickett N600-ES, Apollo 13» . Смитсоновский национальный музей авиации и космонавтики. Архивировано из оригинала 9 октября 2013 г. Проверено 3 сентября 2013 г.

[24] Чарльз Овертон Харрис, Упрощенная логарифмическая линейка , Американское техническое общество, 1961, стр. 5.

[25] Шер, Дэвид Б.; Натаро, Дин К. (2 июня 2009 г.). «Простафаэретическая логарифмическая линейка: механическое устройство умножения, основанное на тригонометрических тождествах» . Математика и компьютерное образование, Vol. 38, вып. 1 (зима 2004 г.): 37–43 . Архивировано из оригинала 10 мая 2005 г. Проверено 20 февраля 2010 г. - через Findarticles.com.

[26] «Правила калибровки Фишера» . natgasedu.com . Архивировано из оригинала 6 января 2010 г. Проверено 6 октября 2009 г.

[27] «Правила полета пилотного воздушного шара» . www.pilotballoon.com . Архивировано из оригинала 28 сентября 2016 г. Проверено 28 сентября 2016 г.

[28] Росс, МГ (2003). «Круг времени: ошибки в использовании колеса для беременных». Журнал медицины матери, плода и новорожденных . 14 (6): 370–372. дои : 10.1080/14767050412331312200 . ПМИД 15061314 . S2CID 20101166 .

[29] «Последствия ядерного оружия» . Проверено 2 мая 2021 г.

[30] «Линейка Стрейнджлав» . Проверено 2 мая 2021 г.

[31] «Ван LOCI-2» . oldcalculatormuseum.com .

[Wang_Ad_1966-32] Ван Лаборатории (декабрь 1966 г.). «Теперь вы можете за несколько минут определить состав сополимера, сидя за столом». Аналитическая химия . 38 (13): 62А–63А. дои : 10.1021/ac50155a005 .

[Leibson_2010-33] Лейбсон, Стивен (2010). «Проект HP 9100: экзотермическая реакция» . Проверено 2 января 2016 г. ^{[ постоянная мертвая ссылка ]}

[Volder_2000-34] Волдер, Джек Э. (июнь 2000 г.). «Рождение CORDIC» (PDF) . Журнал обработки сигналов СБИС . 25 (2): 101–105. дои : 10.1023/а:1008110704586 . ISSN 0922-5773 . S2CID 112881 . Архивировано из оригинала (PDF) 4 марта 2016 г. Проверено 2 января 2016 г.

[35] Беренс, Лоуренс; Розен, Леонард Дж. (1982). Письмо и чтение по учебной программе . Маленький, Браун . п. 273. Затем, всего десять лет назад, изобретение карманного калькулятора почти в мгновение ока сделало логарифмическую линейку устаревшей...

[36] Маор, Эли (2009). е: История числа . Издательство Принстонского университета. п. 16. ISBN 978-0-691-14134-3 . Затем, в начале 1970-х годов, на рынке появились первые электронные ручные калькуляторы, и через десять лет логарифмическая линейка устарела.

[37] Каслден, Родни (2007). Изобретения, изменившие мир . Футура. п. 157. ИСБН 978-0-7088-0786-6 . С изобретением калькулятора логарифмическая линейка мгновенно устарела.

[38] Деннинг, Питер Дж .; Меткалф, Роберт М. (1998). За пределами вычислений: следующие пятьдесят лет вычислений . Спрингер . п. xiv. ISBN 978-0-387-98588-6 . Первый ручной калькулятор появился в 1972 году и в одночасье сделал логарифмическую линейку устаревшей.

[39] Столл, Клифф. «Когда правили правила слайдов», Scientific American, май 2006 г., стр. 80–87 . «Трудность обучения пользованию логарифмическими линейками препятствовала их использованию среди простого народа . Да, случайный менеджер продуктового магазина рассчитывал скидки на палочке, и этот автор однажды поймал своего школьного учителя английского языка, подсчитывающего статистику для победителей тройных скачек на беговой дорожке. Но линейки так и не вошли в повседневную жизнь, потому что с их помощью нельзя было выполнять простое сложение и вычитание, не говоря уже о сложности отслеживания десятичной точки, которые оставались инструментами для технарей».

[40] Уотсон, Джордж Х. «Проблемное обучение и три буквы технологии», Сила проблемного обучения , Барбара Дач, Сьюзан Гро, Дебора Аллен, ред., Stylus Publishing, LLC, 2001. «Численные вычисления в физика и химия для первокурсников были мучительными; однако, похоже, это не касалось тех студентов, которым посчастливилось уже иметь калькулятор. Я хорошо помню, что в конце 1974 года студентам, которые все еще пользовались логарифмическими линейками, давали дополнительные. 15 минут на выпускной экзамен, чтобы компенсировать вычислительное преимущество, обеспечиваемое калькулятором, — едва ли адекватная компенсация, по мнению остальных практикующих логарифмических линеек».

[41] Столл, Клифф. «Когда правили правила слайдов», Scientific American, май 2006 г., стр. 80–87 . «Поскольку вычисления происходили буквально со скоростью руки и при этом не хватало точности, математики работали над упрощением сложных задач. Поскольку линейные уравнения были более дружелюбны к логарифмическим линейкам, чем более сложные функции, ученые изо всех сил пытались линеаризовать математические отношения, часто охватывая высшие порядки. или менее важные термины под ковром вычислений. Таким образом, конструктор автомобилей может рассчитывать расход топлива, глядя в основном на мощность двигателя, игнорируя при этом, как трение воздуха меняется в зависимости от скорости. экономия времени, понимание и понимание. С другой стороны, эти приближения могут скрыть ошибки и привести к грубым ошибкам».

[42] Столл, Клифф. «Когда правили правила слайдов», Scientific American , май 2006 г., стр. 80–87 . «Одним из эффектов было то, что пользователи чувствовали себя близкими к цифрам, осознавая ошибки округления и систематические неточности, в отличие от пользователей сегодняшних программ компьютерного проектирования. Поговорите с инженером из 1950-х годов, и вы, скорее всего, услышите жалобы на те дни, когда расчеты шли рука об руку с более глубоким пониманием. Вместо того, чтобы вводить числа в компьютерную программу, инженер понимал тонкости нагрузок и напряжений, напряжений и токов, углов и расстояний. Числовые ответы, составленные вручную, означали проблему. решение посредством знаний и анализа, а не простого подсчета чисел».

[Williams_2023-43] Уильямс, Эл (21 июня 2023 г.). «Похвала RPN (с Python или C)» . Хакадей . Архивировано из оригинала 23 сентября 2023 г. Проверено 23 сентября 2023 г.

[44] «Citizen Watch Company – Citizen Eco-Drive / США, Канада, Великобритания, ИрландияCitizen Watch» . Citizenwatch.com . Архивировано из оригинала 22 апреля 2014 г. Проверено 21 апреля 2014 г.

[45] «Линейки Грега – ссылки на сборщиков логарифмических линеек» . Sliderule.ozmanor.com. 29 июля 2004 г. Проверено 20 февраля 2010 г.

[ISRM-Restore-46] «Восстановление и исправление правил слайдов и заметок» . Международный музей логарифмических линеек .

[47] «О КОНЦЕНТРАЦИИ» . Краткий.co.jp. Архивировано из оригинала 12 марта 2012 г. Проверено 20 февраля 2010 г.

[thinkgeek1-48] «Линейка» . ДумайГик. Архивировано из оригинала 27 марта 2010 г. Проверено 8 апреля 2015 г.

[thinkgeek2-49] «Линейка» . ДумайГик. Архивировано из оригинала 15 апреля 2012 г. Проверено 8 апреля 2015 г.

[50] «Рехеншибер» . Фабер-Кастелл. Архивировано из оригинала 21 ноября 2013 г. Проверено 17 января 2012 г. Считается, что у них все еще могут быть какие-то линейки, но на их новом веб-сайте и в интернет-магазине их нет.

[51] «Категория общего собрания MIT «Коллекция логарифмических правил» .

[MITnews-52] «Музей MIT соответствует требованиям» . Новости МТИ . Массачусетский технологический институт. 11 января 2005 г. Проверено 1 мая 2019 г.

[MITM-53] «Правила слайдов» . Музей МТИ . Массачусетский технологический институт. Архивировано из оригинала 01 мая 2019 г. Проверено 1 мая 2019 г.

[Proun-54] «Музей MIT — Правила слайдов» . proundesign.com . Проун Дизайн. Архивировано из оригинала 01 мая 2019 г. Проверено 1 мая 2019 г.

[55] Тернер, Кимберли (07 октября 2009 г.). «Линейка: 101». Газеты родного города Колорадо .

[56] «Главный стол библиотеки логарифмических линеек» . Международный музей логарифмических линеек . Архивировано из оригинала 07 января 2023 г. Проверено 7 января 2023 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]