Псевдовыпуклая функция

Эта статья о понятии выпуклого анализа. Для понятия нескольких комплексных переменных см. псевдовыпуклая область .

В выпуклом анализе и вариационном исчислении , обоих разделах математики , псевдовыпуклая функция — это функция , которая ведет себя как выпуклая функция в отношении нахождения своих локальных минимумов , но на самом деле не обязательно должна быть выпуклой. Неформально дифференцируемая функция является псевдовыпуклой, если она возрастает в любом направлении, где она имеет положительную производную . Свойство должно сохраняться во всей области функции, а не только для близлежащих точек.

Формальное определение

Рассмотрим дифференцируемую функцию $f:X\subseteq \mathbb {R} ^{n}\rightarrow \mathbb {R}$, определенный на (непустом) множестве выпуклом открытом $X$ конечномерного евклидова пространства $\mathbb {R} ^{n}$. Эту функцию называют псевдовыпуклой, если выполнено следующее свойство:

для всех $x,y\in X:\quad \nabla f(x)\cdot (y-x)\geq 0\Rightarrow f(y)\geq f(x)$.

Эквивалентно:

для всех $x,y\in X:\quad f(y)<f(x)\Rightarrow \nabla f(x)\cdot (y-x)<0$.

Здесь $\nabla f$ это градиент ​ $f$, определяемый: $\nabla f=\left({\frac {\partial f}{\partial x_{1}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right).$

Обратите внимание, что определение также можно сформулировать в терминах производной по направлению . $f$, в направлении, заданном вектором $v=y-x$. Это потому, что, как $f$ дифференцируема, эта производная по направлению определяется выражением:

${\frac {\partial f}{\partial v}}(x)=\nabla f(x)\cdot v=\nabla f(x)\cdot (y-x).$

Характеристики

Отношение к другим типам «выпуклости»

Любая выпуклая функция является псевдовыпуклой, но обратное неверно. Например, функция $f(x)=x+x^{3}$ псевдовыпуклая, но не выпуклая. Аналогично, любая псевдовыпуклая функция является квазивыпуклой ; но обратное неверно, поскольку функция $f(x)=x^{3}$ является квазивыпуклым, но не псевдовыпуклым. Схематически это можно резюмировать так:

выпуклый $\Rightarrow$ псевдовыпуклый $\Rightarrow$ квазивыпуклый

Функции x^3 (квазивыпуклые, но не псевдовыпуклые) и x^3 + x (псевдовыпуклые и, следовательно, квазивыпуклые). Ни один из них не является выпуклым.

Чтобы увидеть это $f(x)=x^{3}$ не является псевдовыпуклым, рассмотрим его производную при $x=0$: $f^{\prime }(0)=0$. Тогда, если $f(x)=x^{3}$ было псевдовыпуклым, мы должны были иметь:

$f^{\prime }(0)(y-0)=0\geq 0\Rightarrow f(y)\geq f(0),\quad \forall \,y\in \mathbb {R} .$

В частности, это должно быть верно для $y=-1$. Но это не так, поскольку: $f(-1)=(-1)^{3}=-1<f(0)=0$.

Достаточное условие оптимальности

Для любой дифференцируемой функции мы имеем по теореме Ферма , которое гласит: если необходимое условие оптимальности $f$ имеет локальный минимум в $x^{*}$ в открытом домене, то $x^{*}$ должна быть стационарной точкой $f$ (то есть: $\nabla f(x^{*})=0$).

Псевдовыпуклость представляет большой интерес в области оптимизации , поскольку обратное также верно для любой псевдовыпуклой функции. То есть: если $x^{*}$ является стационарной точкой псевдовыпуклой функции $f$, затем $f$ имеет глобальный минимум в $x^{*}$. Также обратите внимание, что результат гарантирует глобальный минимум (а не только локальный).

Этот последний результат верен и для выпуклой функции, но неверен для квазивыпуклой функции. Рассмотрим, например, квазивыпуклую функцию:

$f(x)={\frac {e^{x}}{x^{2}+1}}+{\frac {1}{e^{x}}}$.

Эта функция не псевдовыпуклая, а квазивыпуклая. Кроме того, точка $x=0$ является критической точкой $f$, как $f^{\prime }(0)=0$. Однако, $f$ не имеет глобального минимума в $x=0$ (даже не локальный минимум).

Пример квазивыпуклой функции, не являющейся псевдовыпуклой. Функция имеет критическую точку $x=0$, но это не минимум.

Наконец, обратите внимание, что псевдовыпуклая функция может не иметь критической точки. Возьмем, к примеру, псевдовыпуклую функцию: $f(x)=x^{3}+x$, производная которого всегда положительна: $f^{\prime }(x)=3x^{2}+1>0,\,\forall \,x\in \mathbb {R}$.

Примеры

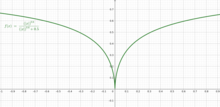
Пример функции, которая является псевдовыпуклой, но не выпуклой: $f(x)={\frac {x^{2}}{x^{2}+k}},\,k>0.$ На рисунке показана эта функция для случая, когда $k=0.2$. Этот пример можно обобщить на две переменные:

$f(x)={\frac {x^{2}+y^{2}}{x^{2}+y^{2}+k}},\,k>0.$

Псевдовыпуклая функция, не являющаяся выпуклой.

Предыдущий пример можно изменить, чтобы получить функцию, которая не является ни выпуклой, ни псевдовыпуклой, а является квазивыпуклой:

$f(x)={\frac {|x|^{p}}{|x|^{p}+k}},\,k>0,\,p\in (0,1).$

На рисунке показана эта функция для случая, когда $k=0.5,p=0.6$. Как видно, эта функция не является выпуклой из-за вогнутости и не является псевдовыпуклой, поскольку не дифференцируема при $x=0$.

Квазивыпуклая функция, которая не является ни выпуклой, ни псевдовыпуклой.

Обобщение на недифференцируемые функции

Понятие псевдовыпуклости можно обобщить на недифференцируемые функции следующим образом. Учитывая любую функцию $f:X\rightarrow \mathbb {R}$, мы можем определить верхнюю Дини производную $f$ к:

$f^{+}(x,u)=\limsup _{h\to 0^{+}}{\frac {f(x+hu)-f(x)}{h}};$

где u — любой единичный вектор . Функция называется псевдовыпуклой, если она возрастает в любом направлении, в котором верхняя производная Дини положительна. Точнее, это характеризуется с помощью субдифференциала $\partial f$ следующее:

Для всех $x,y\in X$: если $x^{*}\in \partial f(x)$ таков, что $\langle x^{*},y-x\rangle \geq 0$, затем $f(x)\leq f(z)$, для всех $z\in [x,y]$;

где $[x,y]$ обозначает отрезок прямой, примыкающий к x и y .

Связанные понятия

А псевдовогнутая функция — это функция, отрицательная функция которой является псевдовыпуклой. А псевдолинейная функция – это функция, которая одновременно псевдовыпуклая и псевдовогнутая. Например, дробно-линейные программы имеют псевдолинейные целевые функции и ограничения линейного неравенства . Эти свойства позволяют решать дробно-линейные задачи с помощью варианта симплексного алгоритма ( Джорджа Б. Данцига ).

Дана векторная функция $\eta$существует более общее понятие $\eta$-псевдовыпуклость и $\eta$-псевдолинейность; при этом классическая псевдовыпуклость и псевдолинейность относятся к случаю, когда $\eta (x,y)=y-x$.

См. также

• Псевдовыпуклость
• Выпуклая функция
• Квазивыпуклая функция
• Функция инвекс

Ссылки

• Флудас, Христодулос А .; Пардалос, Панос М. (2001), «Обобщенные монотонные многозначные карты», Энциклопедия оптимизации , Springer, стр. 227, ISBN  978-0-7923-6932-5 .
• Мангасарян, О.Л. (январь 1965 г.). «Псевдовыпуклые функции». Журнал Общества промышленной и прикладной математики, серия А. 3 (2): 281–290. дои : 10.1137/0303020 . ISSN   0363-0129 . .
• Рапчак, Т. (15 февраля 1991 г.). «О псевдолинейных функциях». Европейский журнал операционных исследований . 50 (3): 353–360. дои : 10.1016/0377-2217(91)90267-Y . ISSN   0377-2217 .