Долгота периапсиса
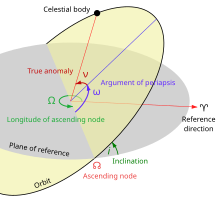
В небесной механике долгота периапсиса , также называемая долготой перицентра вращающегося тела, — это долгота (измеренная от точки весеннего равноденствия), на которой произошел бы периапсис (наименьшее сближение с центральным телом), если бы орбиты тела наклонение было равно нулю. Обычно его обозначают ϖ .
Для движения планеты вокруг Солнца это положение называется долготой перигелия ϖ, которая представляет собой сумму долготы восходящего узла Ω и аргумента перигелия ω. [1] [2]
Долгота периапсиса представляет собой составной угол, часть которого измеряется в плоскости отсчета , а остальная часть измеряется в плоскости орбиты . Аналогично, любой угол, полученный из долготы периапсиса (например, средняя долгота и истинная долгота ), также будет составным.
Иногда термин долгота перицентра используется для обозначения ω , угла между восходящим узлом и перицентром. Такое использование этого термина особенно распространено при обсуждении двойных звезд и экзопланет. [3] [4] Однако угол ω менее двусмысленно известен как аргумент перицентра .
Расчет по векторам состояния
[ редактировать ]ϖ представляет собой сумму долготы восходящего узла Ω (измеренной в плоскости эклиптики) и аргумента периапсиса ω (измеренной в плоскости орбиты):
которые получены из векторов орбитального состояния .
Вывод эклиптической долготы и широты перигелия для наклонных орбит.
[ редактировать ]Определите следующее:
- я, склонность
- ω, аргумент перигелия
- Ω, долгота восходящего узла
- ε, наклон эклиптики (для стандартного равноденствия 2000,0 года используйте 23,43929111°)
Затем:
- A = cos ω cos Ω – sin ω sin Ω cos i
- B = cos ε (cos ω sin Ω + sin ω cos Ω cos i) – sin ε sin ω sin i
- C = sin ε (cos ω sin Ω + sin ω cos Ω cos i) + cos ε sin ω sin i
Прямое восхождение α и склонение δ направления перигелия равны:
Если A < 0, добавьте 180° к α, чтобы получить правильный квадрант.
Эклиптическая долгота ϖ и широта b перигелия равны:
Если cos(α) < 0, добавьте 180° к ϖ, чтобы получить правильный квадрант.
В качестве примера использованы самые свежие цифры Брауна (2017). [5] для гипотетической Девятой Планеты с i = 30°, ω = 136,92° и Ω = 94°, тогда α = 237,38°, δ = +0,41° и ϖ = 235,00°, b = +19,97° (на самом деле Браун указывает i, Ω и ϖ, из которых было вычислено ω).
Ссылки
[ редактировать ]- ^ Урбан, Шон Э.; Зайдельманн, П. Кеннет (ред.). «Глава 8: Орбитальные эфемериды Солнца, Луны и планет» (PDF) . Пояснительное приложение к Астрономическому альманаху . Университетские научные книги. п. 26.
- ^ Саймон, Дж.Л.; и др. (1994). «Численные выражения для формул прецессии и средних элементов для Луны и планет». Астрономия и астрофизика . 282 : 663–683, 672. Бибкод : 1994A&A...282..663S .
- ^ Роберт Грант Эйткен (1918). Двойные звезды . Публикации полувекового юбилея Калифорнийского университета. Округ Колумбия Макмертри. п. 201 .
- ^ «Формат». Архивировано 25 февраля 2009 г. в Wayback Machine в Шестом каталоге орбит визуальных двойных звезд. Архивировано 12 апреля 2009 г. в Wayback Machine , Уильям И. Харткопф и Брайан Д. Мейсон, Военно-морская обсерватория США, Вашингтон, DC, доступ осуществлен 10 января 2018 г.
- ^ Браун, Майкл Э. (2017) «Девятая планета: где ты? (часть 1)» В поисках девятой планеты. http://www.findplanetnine.com/2017/09/planet-nine-where-are-you-part-1.html
Внешние ссылки
[ редактировать ]- Определение параметров орбиты Земли . Прошлая и будущая долгота перигелия Земли.
