Вертолетный куб

Вертолетный кубик — это головоломка, похожая на кубик Рубика, изобретенная Адамом Г. Коуэном в 2005 году и построенная в 2006 году. ^[1]^[2]^[3]^[4]^[5]^[6]^[7] Он также имеет форму куба . На первый взгляд Helicopter Cube может показаться комбинацией 2x2x2 и Skewb , но на самом деле он режется по-другому и вращается вокруг ребер куба, а не вокруг граней куба. Цель головоломки — перемешать цвета, а затем вернуть их в исходное состояние — по одному цвету на грань.

Описание

Вертолетный куб выполнен в форме куба, разрезанного на 8 угловых частей и 24 грани в центре. Каждая угловая часть имеет три цвета, а каждая центральная часть лицевой стороны имеет только один цвет. В отличие от кубика Рубика, его грани не вращаются; скорее, кусочки перемешиваются путем вращения вокруг края куба.

При повороте головоломки поворот на 180° меняет местами две угловые части и две пары центральных частей грани, но сохраняет форму куба. Таким образом можно разгадать всю головоломку.

Однако также возможно повернуть кромку на ~71°, так что основание двух групп угловой детали и центральной лицевой детали будет совмещено с плоскостью вращения другой кромки. Затем второй край можно повернуть, таким образом перемешав угловые части и центральные части грани и придав головоломке некубическую форму. Этот вид перемешивания известен как перемешивание . Из-за различной формы смешанных частей некоторые вращения, возможные в кубической форме, могут оказаться невозможными в перемешанной форме. Используя комбинацию таких «беспорядочных» ходов, можно вернуться к кубической форме, но с некоторыми центральными частями грани в неправильной ориентации, таким образом выступающими наружу, как шипы, а не лежащими ровно на грани куба. Могут быть внесены и более тонкие изменения, которые описаны ниже.

Существует четыре варианта Вертолетного куба:

оригинальный Helicopter Cube, произведенный The Twisty Store (также продаваемый Уве Меффертом ), состоящий только из 8 угловых частей и 24 центральных лицевых частей;
«Пышный вертолет» Тома ван дер Зандена, ^[4] который имеет дополнительные 12 кромок по 2 цвета каждая. Это требует от человека строить по краям, тогда как в кубе вертолета они спрятаны внизу, и не имеет значения, где вы строите.
«Curvy Copter Plus», также созданный Томом ван дер Занденом, с дополнительными вырезами посередине центральных частей лица, что позволяет головоломке еще больше перепутаться;
«Helicopter Skewb», также созданный Томом Ван Дер Занденом, который выглядит точно так же, как оригинальный Helicopter Cube, но также может вращаться, как Skewb .
«Пышный коптер 3», 2014 года выпуска, компания mf8.

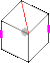
Поворот ~71° для подготовки к неуклюжему движению.

Решения

Вертолетный куб Мефферта, белый корпус, собранный

Если головоломку можно решить только с поворотами на 180°, то ее можно решить только с поворотами на 180°. Однако, если были сделаны какие-то неупорядоченные ходы, даже если головоломка впоследствии была возвращена в форму куба, решить ее, используя только повороты на 180°, может быть невозможно. Причина этого в том, что при повороте только на 180° каждая центральная часть грани может быть переставлена только в пределах 6-членного цикла, часто называемого его орбитой . ^[6] Центральные части граней, находящиеся на разных орбитах, не могут быть заменены с помощью поворота только на 180°. Однако беспорядочные ходы могут переставлять центральные части лица между разными орбитами, в результате чего головоломка остается в состоянии, которое невозможно решить только поворотами на 180 °.

Количество комбинаций

Предположим, что Helicopter Cube перемешивается без перепутывания движений (т.е. с поворотами только на 180 градусов). Возможны любые перестановки углов, в том числе нечетные. Семь углов можно вращать независимо, а ориентация восьмого зависит от остальных семи, что дает 8! ×3 ⁷ комбинации.

Всего имеется 24 лицевых центра, которые можно объединить в 24! разные способы. Но центры лица на самом деле располагаются на четырех различных орбитах, каждая из которых содержит все цвета. Таким образом, количество перестановок сокращается до 6! ⁴ распоряжения. ^[8] Перестановка центров граней четная, количество перестановок делится на 2.

Если предположить, что куб не имеет фиксированной ориентации в пространстве и что перестановки, возникающие в результате вращения куба без его скручивания, считаются одинаковыми, количество перестановок уменьшается в 24 раза. Это связано с тем, что все 24 возможных положения и ориентации куба первые углы эквивалентны из-за отсутствия фиксированных центров. Этот фактор не появляется при расчете перестановок кубов N×N×N, где N нечетно, поскольку эти головоломки имеют фиксированные центры, которые определяют пространственную ориентацию куба.

Это дает общее количество перестановок

{\frac {7!\cdot 3^{6}\cdot 6!^{4}}{2}}\approx 4.94\times 10^{17}.

Расширенное число составляет 493 694 233 804 800 000 (приблизительно 494 биллиарда в длинной шкале или 494 квадриллиона в короткой шкале). ^[6]

Когда вертолетный куб перемешивается беспорядочными движениями, но все еще сохраняет свою форму куба, то центры граней не встречаются на четырех различных орбитах. Если предположить, что четыре центра каждого цвета неразличимы, то число перестановок сокращается до 24!/(4! ⁶) распоряжения. Понижающий коэффициент возникает потому, что существует 24 (4!) способа расставить четыре фигуры данного цвета. Это возведено в шестую степень, потому что цветов шесть.

Это дает общее количество перестановок

{\frac {7!\cdot 3^{6}\cdot 24!}{4!^{6}}}.

Расширенное число составляет 11 928 787 020 628 077 600 000 (приблизительно 11 929 триллионов или 12 триллионов по длинной шкале или 12 секстиллионов по короткой шкале). ^[8]

Чтобы подсчитать позиции, не являющиеся кубами, нам нужно посчитать все возможные фигуры (игнорируя цвета). Подсчитать эти фигуры сложно, поскольку иногда ходы блокируются исключительно из-за формы фигур, а не из-за основного механизма. Мэтт Галла провел полный анализ и описал свои результаты в этом посте на форуме TwistyPuzzles. Я воспроизвел и проверил его результаты. Он нашел 14 098 фигур, или 28 055, если считать и зеркальные изображения. Однако некоторые из них обладают симметрией и поэтому встречаются менее чем в 24 (или 48) возможных ориентациях. Вот разбивка этих симметрий: ^[8]


Сим.		мистер ₄ р ₃ р ₂	mr₃r_мр3р2	r₃r_r3r2	м _ж р _2е	м _е р _2е	р _2е р _2е	м ₄	мне	р _2е	р _2ф	м _с	я	Общий
	Международный	Ой	Д _3д	Д ₃	С _{2 в}	С _{2 часа}	D_Д2	С ₄	С _с	С ₂	С ₂	S_S2	С ₁
	Хороший.	м 3 м	3 m	322	мм2	2/м	222	4	м	2	2	1	1
Заказ		48	12	6	4	4	4	4	2	2	2	2	1
Индекс		1	4	8	12	12	12	12	24	24	24	24	48
Формы зеркальное изображение		1	1	8	1	18	4	1	82	764	5	37	13,176	14,098
Формы зеркальное изображение		1	1	16	1	18	8	1	82	1,528	10	37	26,352	28,055
Общий		1	4	128	12	216	96	12	1,968	36,672	240	888	1,264,896	1,305,133

В строке «Порядок» указаны размеры групп симметрии. Индекс — это индекс группы симметрии как подгруппы полной кубической группы симметрии, т. е. он равен 48, разделенным на порядок. Индекс также представляет собой количество способов, которыми любая конкретная форма с такой симметрией может быть ориентирована в пространстве (включая отражения). В первой строке «Фигуры» указано количество фигур, которые Мэтт нашел для каждой группы симметрии, не считая зеркальных изображений, а вторая строка «Фигуры» включает в себя фигуры зеркальных изображений. Строка с пометкой «Итого» представляет собой произведение индекса и количества фигур. ^[8]

Умножение этого результата на предыдущий результат дает 15 568 653 590 593 384 802 320 800 000 (приблизительно 15 569 квадриллионов или 15 квадриллионов по длинной шкале или 15 октиллионов по короткой шкале) смешанных позиций в целом. ^[8]

См. также

Square One (головоломка) — еще одна кубическая головоломка, меняющая форму.

Ссылки

^ "Вертолетные кубики Черное тело" . Мефферта. Архивировано из оригинала 14 июля 2011 г. Проверено 1 сентября 2010 г. Вертолетный куб был задуман Адамом Коуэном в 2005 году, но был построен только в 2006 году, когда Адам обнаружил, что для изготовления деталей можно использовать 3D-печать.
^ «Вертолет-куб – Белое тело» . Puzzle Master Inc. Архивировано из оригинала 6 июля 2011 г. Проверено 1 сентября 2010 г.
^ Гетц Швандтнер. «Вертолетный куб белый» . Чрезвычайно загадочно . Проверено 1 сентября 2010 г. Разработано: Адам Коуэн
^ Jump up to: ^а ^б Том ван дер Занден. «Пышный вертолет» . Проверено 1 сентября 2010 г. Curvy Copter — моя самая популярная головоломка. Это вариация «Вертолетного куба» Адама Г. Коуэна.
^ «Система запутанных головоломок» . Архивировано из оригинала 7 августа 2010 г. Проверено 1 сентября 2010 г. Вертолетный куб был спроектирован и построен Адамом Г. Коуэном (Puzzlemaster42) и Кацухико Окамото (Кацухико) в 2007 году.
^ Jump up to: ^а ^б ^с «L'Helicopter Cube (французский)» . фан2куб . Проверено 1 сентября 2010 г.
^ Джейсон Смит. «Массовое производство вертолетного куба Адама Коуэна - 4/2010» . Головоломка . Проверено 1 сентября 2010 г.
^ Jump up to: ^а ^б ^с ^д ^и Шерфуис, Яап (12 декабря 2017 г.). «Вертолетный куб» .

[1] "Вертолетные кубики Черное тело" . Мефферта. Архивировано из оригинала 14 июля 2011 г. Проверено 1 сентября 2010 г. Вертолетный куб был задуман Адамом Коуэном в 2005 году, но был построен только в 2006 году, когда Адам обнаружил, что для изготовления деталей можно использовать 3D-печать.

[2] «Вертолет-куб – Белое тело» . Puzzle Master Inc. Архивировано из оригинала 6 июля 2011 г. Проверено 1 сентября 2010 г.

[3] Гетц Швандтнер. «Вертолетный куб белый» . Чрезвычайно загадочно . Проверено 1 сентября 2010 г. Разработано: Адам Коуэн

[zanden-4] Jump up to: ^а ^б Том ван дер Занден. «Пышный вертолет» . Проверено 1 сентября 2010 г. Curvy Copter — моя самая популярная головоломка. Это вариация «Вертолетного куба» Адама Г. Коуэна.

[5] «Система запутанных головоломок» . Архивировано из оригинала 7 августа 2010 г. Проверено 1 сентября 2010 г. Вертолетный куб был спроектирован и построен Адамом Г. Коуэном (Puzzlemaster42) и Кацухико Окамото (Кацухико) в 2007 году.

[fan2cube-6] Jump up to: ^а ^б ^с «L'Helicopter Cube (французский)» . фан2куб . Проверено 1 сентября 2010 г.

[7] Джейсон Смит. «Массовое производство вертолетного куба Адама Коуэна - 4/2010» . Головоломка . Проверено 1 сентября 2010 г.

[jaapsch-8] Jump up to: ^а ^б ^с ^д ^и Шерфуис, Яап (12 декабря 2017 г.). «Вертолетный куб» .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]