Пластичность (физика)

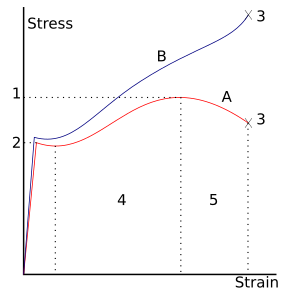
- Абсолютная сила
- Предел текучести (предел текучести)
- Разрыв
- деформационного упрочнения Область
- шейки Область
- Кажущееся напряжение ( F / A 0 )
- Фактическое напряжение ( F / A )
| Часть серии о |
| Механика сплошных сред |
|---|
В физике и материаловедении ) — пластичность (также известная как пластическая деформация это способность твердого материала подвергаться остаточной деформации — необратимому изменению формы в ответ на приложенные силы. [ 1 ] [ 2 ] Например, твердый кусок металла, сгибаемый или придаваемый ему новой формы, демонстрирует пластичность, поскольку внутри самого материала происходят необратимые изменения. В технике переход от упругого поведения к пластическому называется текучестью .
Пластическая деформация наблюдается в большинстве материалов, особенно в металлах , грунтах , камнях , бетоне и пенопластах . [ 3 ] [ 4 ] [ 5 ] [ 6 ] Однако физические механизмы, вызывающие пластическую деформацию, могут сильно различаться. В кристаллическом масштабе пластичность металлов обычно является следствием дислокаций . Такие дефекты относительно редки в большинстве кристаллических материалов, но многочисленны в некоторых частях их кристаллической структуры; в таких случаях пластическая кристалличность может возникнуть . В хрупких материалах, таких как камень, бетон и кость, пластичность обусловлена преимущественно скольжением по микротрещинам . В ячеистых материалах, таких как жидкие пены или биологические ткани , пластичность является главным образом следствием перестановок пузырьков или клеток, особенно процессов Т1 .
Для многих пластичных металлов растягивающая нагрузка , приложенная к образцу, приводит к тому, что он ведет себя упруго. Каждое увеличение нагрузки сопровождается пропорциональным увеличением растяжения. При снятии нагрузки деталь возвращается к исходному размеру. Однако, как только нагрузка превышает пороговое значение – предел текучести – растяжение увеличивается быстрее, чем в упругой области; теперь, когда нагрузка снимается, некоторая степень растяжения сохраняется.
Однако упругая деформация является приближением, и ее качество зависит от рассматриваемых временных рамок и скорости нагружения. Если, как указано на графике напротив, деформация включает упругую деформацию, ее также часто называют «упруго-пластической деформацией» или «упруго-пластической деформацией».
Совершенная пластичность – это свойство материалов подвергаться необратимой деформации без увеличения напряжений и нагрузок. Пластиковые материалы, которые были упрочнены предварительной деформацией, например, холодной штамповкой , могут нуждаться в более высоких напряжениях для дальнейшей деформации. Как правило, пластическая деформация также зависит от скорости деформации, т.е. для увеличения скорости деформации обычно необходимо прикладывать более высокие напряжения. Говорят, что такие материалы деформируются вязкопластически .
Содействующие свойства
[ редактировать ]Пластичность материала прямо пропорциональна пластичности и ковкости материала .
Физические механизмы
[ редактировать ]
В металлах
[ редактировать ]Пластичность кристалла чистого металла обусловлена прежде всего двумя видами деформации кристаллической решетки: скольжением и двойникованием. Скольжение — это сдвиговая деформация, которая перемещает атомы на множество межатомных расстояний относительно их начальных положений. Двойникование — это пластическая деформация, происходящая в двух плоскостях под действием комплекса сил, приложенных к данной металлической детали.
Большинство металлов проявляют большую пластичность в горячем состоянии, чем в холодном. Свинец проявляет достаточную пластичность при комнатной температуре, тогда как чугун не обладает достаточной пластичностью для любой операции ковки, даже в горячем состоянии. Это свойство имеет важное значение при операциях формования, формования и экструзии металлов. Большинство металлов при нагревании становятся пластичными и, следовательно, приобретают горячую форму.
Скользящие системы
[ редактировать ]Кристаллические материалы содержат однородные плоскости атомов, организованные с дальним порядком. Самолеты могут проскальзывать мимо друг друга в плотно упакованных направлениях, как показано на странице систем скольжения. Результатом является постоянное изменение формы кристалла и пластическая деформация. Наличие дислокаций увеличивает вероятность самолетов.
Обратимая пластичность
[ редактировать ]На наномасштабе первичная пластическая деформация в простых гранецентрированных кубических металлах обратима до тех пор, пока нет переноса материала в виде поперечного скольжения . [ 7 ] Сплавы с памятью формы, такие как нитиноловая проволока, также обладают обратимой формой пластичности, которую правильнее называть псевдоэластичностью .
Срезная полосатость
[ редактировать ]Наличие других дефектов внутри кристалла может запутывать дислокации или иным образом препятствовать их скольжению. Когда это происходит, пластичность локализуется в определенных участках материала. Для кристаллов эти области локализованной пластичности называются полосами сдвига .
Микропластичность
[ редактировать ]Микропластичность — локальное явление в металлах. Это происходит при значениях напряжения , когда металл в целом находится в упругой области, а некоторые локальные области находятся в пластической области. [ 8 ]
Аморфные материалы
[ редактировать ]Сумасшедший
[ редактировать ]В аморфных материалах разговор о «дислокациях» неприменим, поскольку во всем материале отсутствует дальний порядок. Эти материалы все еще могут подвергаться пластической деформации. Поскольку аморфные материалы, как и полимеры, не упорядочены должным образом, они содержат большое количество свободного объема или ненужного пространства. Растягивание этих материалов открывает эти области и может придать материалам мутный вид. Эта мутность является результатом растрескивания , когда фибриллы образуются внутри материала в областях высокого гидростатического напряжения . Внешний вид материала может измениться: от упорядоченного до «сумасшедшего» рисунка от растяжений и растяжек.
Ячеистые материалы
[ редактировать ]Эти материалы пластически деформируются, когда изгибающий момент превышает полностью пластический момент. Это относится к пенопластам с открытыми порами, где изгибающий момент действует на стенки ячеек. Пенопласты могут быть изготовлены из любого материала с пределом пластичности, включая жесткие полимеры и металлы. Этот метод моделирования пены балками справедлив только в том случае, если отношение плотности пены к плотности вещества меньше 0,3. Это связано с тем, что балки податливы в осевом направлении, а не изгибаются. В пенопластах с закрытыми порами предел текучести увеличивается, если материал находится под напряжением из-за мембраны, охватывающей лицевую поверхность ячеек.
Почвы и песок
[ редактировать ]Почвы, особенно глины, проявляют значительную неэластичность под нагрузкой. Причины пластичности почв могут быть весьма сложными и сильно зависят от микроструктуры , химического состава и содержания воды. Пластическое поведение почв обусловлено прежде всего перестройкой скоплений соседних зерен.
Камни и бетон
[ редактировать ]Неупругие деформации горных пород и бетона обусловлены, прежде всего, образованием микротрещин и скользящими движениями относительно этих трещин. При высоких температурах и давлениях на пластическое поведение может также влиять движение дислокаций в отдельных зернах микроструктуры.
Независимая от времени текучесть и пластическое течение в кристаллических материалах
[ редактировать ]Независимое от времени пластическое течение как в монокристаллах, так и в поликристаллах определяется критическим/максимальным разрешенным сдвиговым напряжением ( τ CRSS ), инициирующим миграцию дислокаций вдоль параллельных плоскостей скольжения одиночной системы скольжения, тем самым определяя переход от упругого к пластическому деформационному поведению в кристаллические материалы.
Независимая от времени текучесть и пластическое течение в монокристаллах
[ редактировать ]Критическое разрешенное напряжение сдвига для монокристаллов определяется законом Шмида τ CRSS = σ y /m, где σ y — предел текучести монокристалла, а m — фактор Шмида. Коэффициент Шмида состоит из двух переменных λ и φ, определяющих угол между направлением плоскости скольжения и приложенной растягивающей силой, а также угол между нормалью к плоскости скольжения и приложенной растягивающей силой соответственно. Примечательно, что поскольку m > 1, σ y > τ CRSS .
Критическая разрешенная зависимость напряжения сдвига от температуры, скорости деформации и точечных дефектов
[ редактировать ]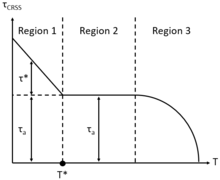
Существуют три характерные области критического разрешенного напряжения сдвига в зависимости от температуры. В области низких температур 1 ( T ≤ 0,25 T m ) скорость деформации должна быть высокой для достижения высокого τ CRSS , который необходим для инициирования скольжения дислокаций и, что эквивалентно, пластического течения. В области 1 критическое разрешенное сдвиговое напряжение имеет две составляющие: атермическое ( τ a ) и тепловое ( τ *) напряжения сдвига, возникающие из-за напряжений, необходимых для перемещения дислокаций при наличии других дислокаций, и сопротивления точечных дефектных препятствий миграция дислокаций соответственно. При T = T умеренная температурная область 2 (0,25 T m < T < 0,7 T m * определяется ), где компонента термического напряжения сдвига τ * → 0, представляющая собой устранение сопротивления точечных дефектов миграции дислокаций. Таким образом, независимое от температуры критическое разрешенное напряжение сдвига τ CRSS = τ a остается таким до тех пор, пока не будет определена область 3. Примечательно, что в области 2 следует учитывать зависящие от времени механизмы пластической деформации (ползучести) при умеренной температуре, такие как сопротивление растворенного вещества. Кроме того, в области высоких температур 3 ( T ≥ 0,7 T m ) έ может быть низким, что способствует низкому τ CRSS , однако пластическое течение все равно будет происходить из-за термически активированных высокотемпературных механизмов пластической деформации, зависящих от времени, таких как диффузионный поток Набарро-Херринга (NH) и Кобла через решетку. и вдоль поверхности монокристалла соответственно, а также ползучесть-скольжение дислокаций.
Стадии нестационарного пластического течения, пост-деформация
[ редактировать ]
На стадии легкого скольжения 1 скорость наклепа, определяемая изменением напряжения сдвига по отношению к деформации сдвига ( dτ / dγ ), низкая, что соответствует небольшому приложенному напряжению сдвига, необходимому для возникновения большой деформации сдвига. . Легкое скольжение дислокаций и соответствующее течение объясняются миграцией дислокаций только по параллельным плоскостям скольжения (т.е. по одной системе скольжения). Умеренное сопротивление миграции дислокаций вдоль параллельных плоскостей скольжения проявляется в связи со слабым взаимодействием полей напряжений между этими дислокациями, которое усиливается при уменьшении межплоскостного расстояния. В целом эти мигрирующие дислокации внутри единой системы скольжения действуют как слабые препятствия течению, и наблюдается умеренное повышение напряжения по сравнению с пределом текучести. Во время стадии 2 линейного упрочнения течения скорость наклепа становится высокой, поскольку для преодоления взаимодействия полей напряжений дислокаций, мигрирующих по непараллельным плоскостям скольжения (т. е. множественных систем скольжения), требуется значительное напряжение, действующее как сильные препятствия течению. Для обеспечения непрерывной миграции дислокаций при небольших деформациях требуется большое напряжение. Напряжение сдвигового течения прямо пропорционально корню квадратному из плотности дислокаций (τ поток ~ р ½ ), независимо от эволюции конфигураций дислокаций, что свидетельствует о зависимости упрочнения от количества присутствующих дислокаций. Что касается этой эволюции конфигураций дислокаций, то при малых деформациях расположение дислокаций представляет собой случайный трехмерный массив пересекающихся линий. Умеренные деформации соответствуют ячеистым дислокационным структурам с неоднородным распределением дислокаций с большой плотностью дислокаций на границах ячеек и малой плотностью дислокаций внутри клетки. При еще большей деформации ячеистая дислокационная структура уменьшается в размерах до тех пор, пока не будет достигнут минимальный размер. Наконец, скорость наклепа снова становится низкой при истощении/насыщении стадии упрочнения 3 пластического течения, поскольку небольшие напряжения сдвига вызывают большие деформации сдвига. Примечательно, что в тех случаях, когда множественные системы скольжения ориентированы благоприятно по отношению к приложенному напряжению, τ CRSS для этих систем может быть одинаковым, и текучесть может происходить в соответствии с миграцией дислокаций вдоль множественных систем скольжения с непараллельными плоскостями скольжения, демонстрируя работу стадии 1. -скорость закалки, обычно характерная для стадии 2. Наконец, ниже суммировано различие между независимой от времени пластической деформацией в объемноцентрированных кубических переходных металлах и гранецентрированных кубических металлах.
| Объемноцентрированные кубические переходные металлы | Гранецентрированные кубические металлы |
|---|---|
| Критическое разрешенное напряжение сдвига = высокое (относительно) и сильно зависящее от температуры. | Критическое разрешенное напряжение сдвига = низкое (относительно) и слабо зависящее от температуры. |
| Скорость упрочнения = не зависит от температуры | Скорость упрочнения = зависит от температуры |
| Деформация шейки увеличивается с температурой | Деформация шейки уменьшается с температурой |
Независимая от времени текучесть и пластическое течение в поликристаллах.
[ редактировать ]Пластичность в поликристаллах существенно отличается от таковой в монокристаллах из-за наличия плоских зернограничных (ЗГ) дефектов, которые действуют как очень сильные препятствия пластическому течению, препятствуя миграции дислокаций по всей длине активированной плоскости (плоскостей) скольжения. Следовательно, дислокации не могут переходить из одного зерна в другое через границу зерна. В следующих разделах рассматриваются конкретные требования GB для обширной пластической деформации поликристаллов перед разрушением, а также влияние микроскопической текучести внутри отдельных кристаллитов на макроскопическую текучесть поликристалла. Критическое разрешенное напряжение сдвига для поликристаллов также определяется законом Шмида (τ CRSS = σ y /ṁ), где σ y — предел текучести поликристалла, а ṁ — взвешенный коэффициент Шмида. Взвешенный фактор Шмида отражает наименее благоприятно ориентированную систему скольжения среди наиболее благоприятно ориентированных систем скольжения зерен, составляющих ГБ.
Ограничение границ зерен в поликристаллах
[ редактировать ]Ограничение ГБ для поликристаллов можно объяснить, рассматривая границу зерна в плоскости xz между двумя монокристаллами A и B одинакового состава, структуры и систем скольжения, но разориентированными относительно друг друга. Чтобы гарантировать, что между индивидуально деформируемыми зернами не образуются пустоты, ограничение GB для бикристалла выглядит следующим образом: ε хх А = ε хх Б (х-осевая деформация на ГБ должна быть эквивалентна для A и B), ε zz А = е zz Б (осевая деформация z в ГБ должна быть эквивалентна для A и B), а ε xz А = е хz Б (деформация сдвига xz вдоль плоскости xz-GB должна быть эквивалентна для A и B). Кроме того, это ограничение ГБ требует, чтобы пять независимых систем скольжения были активированы на каждый кристаллит, составляющий ГБ. Примечательно, что поскольку независимые системы скольжения определяются как плоскости скольжения, на которых миграция дислокаций не может быть воспроизведена какой-либо комбинацией миграций дислокаций вдоль плоскостей другой системы скольжения, количество геометрических систем скольжения для данной кристаллической системы, которые по определению могут быть построены с помощью скольжения, системных комбинаций - обычно больше, чем у независимых систем скольжения. Примечательно, что для каждой из семи кристаллических систем существует максимум пять независимых систем скольжения, однако не все семь кристаллических систем достигают этого верхнего предела. Фактически, даже внутри данной кристаллической системы состав и решетка Браве разнообразят количество независимых систем скольжения (см. таблицу ниже). В тех случаях, когда кристаллиты поликристалла не образуют пять независимых систем скольжения, условие ГБ не может быть выполнено, и, таким образом, независимая от времени деформация отдельных кристаллитов приводит к появлению трещин и пустот в ГБ поликристалла, и вскоре реализуется разрушение. . Следовательно, для данного состава и структуры монокристалл с менее чем пятью независимыми системами скольжения прочнее (проявляет большую пластичность), чем его поликристаллическая форма.
| Решетка Браве | Основной класс материала: # Независимые системы скольжения |
|---|---|
| Гранецентрированный кубический | Металл: 5, керамика (ковалентная): 5, керамика (ионная): 2 |
| Телоцентрированная кубическая | Металл: 5 |
| Простой кубический | Керамический (ионный): 3 |
| Шестиугольный | Металл: 2, керамика (смешанная): 2 |
Последствия зернограничных ограничений в поликристаллах
[ редактировать ]Хотя два кристаллита A и B, обсуждавшиеся в предыдущем разделе, имеют идентичные системы скольжения, они неправильно ориентированы друг относительно друга и, следовательно, неправильно ориентированы относительно приложенной силы. Таким образом, микроскопическая текучесть внутри кристаллита может происходить в соответствии с правилами, регулирующими независимую от времени текучесть монокристалла. В конце концов, активированные плоскости скольжения внутри зерен позволят дислокациям мигрировать в ГБ, где многие дислокации затем накапливаются как геометрически необходимые дислокации. Это скопление соответствует градиентам деформации в отдельных зернах, поскольку плотность дислокаций вблизи ГБ больше, чем внутри зерна, создавая напряжение на соседнем зерне, находящемся в контакте. Если рассматривать бикристалл AB в целом, то наиболее выгодно ориентированной системой скольжения в A будет не та, что в B, и, следовательно, τ А CRSS ≠ τ Б КРСС . Первостепенное значение имеет тот факт, что макроскопическая текучесть бикристалла продлевается до тех пор, пока не будет достигнуто более высокое значение τ CRSS между зернами A и B в соответствии с ограничением ГБ. Таким образом, при данном составе и структуре поликристалл с пятью независимыми системами скольжения прочнее (большая степень пластичности), чем его монокристаллическая форма. Соответственно, скорость наклепа будет выше для поликристалла, чем для монокристалла, поскольку для возникновения деформаций в поликристалле требуется большее напряжение. Важно отметить, что, как и в случае напряжения течения монокристалла, τ течения ~ρ ½ , но также обратно пропорциональна корню квадратному из среднего диаметра зерна (τ поток ~d -½ ). Следовательно, напряжение течения поликристалла и, следовательно, прочность поликристалла увеличиваются с малым размером зерна. Причина этого в том, что зерна меньшего размера имеют относительно меньшее количество плоскостей скольжения, которые необходимо активировать, что соответствует меньшему количеству дислокаций, мигрирующих к границам границ, и, следовательно, меньшему напряжению, возникающему в соседних зернах из-за скопления дислокаций. Кроме того, для данного объема поликристалла более мелкие зерна представляют собой более прочные границы зерен-препятствий. Эти два фактора позволяют понять, почему начало макроскопического течения в мелкозернистых поликристаллах происходит при больших приложенных напряжениях, чем в крупнозернистых поликристаллах.
Математические описания
[ редактировать ]Теория деформации
[ редактировать ]
Существует несколько математических описаний пластичности. [ 12 ] Одним из них является теория деформации (см., например, закон Гука ), где тензор напряжений Коши (порядка d-1 в измерениях d) является функцией тензора деформации. Хотя это описание является точным, когда небольшая часть материи подвергается возрастающей нагрузке (например, деформационной нагрузке), эта теория не может объяснить необратимость.
Пластичные материалы могут выдерживать большие пластические деформации без разрушения . Однако даже пластичные металлы разрушаются, когда деформация становится достаточно большой — это происходит в результате деформационного упрочнения материала, в результате чего он становится хрупким . Термическая обработка, такая как отжиг, может восстановить пластичность обработанной детали, чтобы можно было продолжить формование.
Теория пластичности течения
[ редактировать ]В 1934 году Эгон Орован , Майкл Поланьи и Джеффри Ингрэм Тейлор примерно одновременно поняли, что пластическую деформацию пластичных материалов можно объяснить с точки зрения теории дислокаций . Математическая теория пластичности, теория пластичности течения , использует набор нелинейных, неинтегрируемых уравнений для описания набора изменений деформации и напряжения по сравнению с предыдущим состоянием и небольшого увеличения деформации.
Критерии доходности
[ редактировать ]
Если напряжение превысит критическую величину, как уже говорилось выше, материал подвергнется пластической, или необратимой, деформации. Это критическое напряжение может быть растягивающим или сжимающим. Критерии Треска и фон Мизеса обычно используются для определения текучести материала. Однако эти критерии оказались недостаточными для широкого спектра материалов, и некоторые другие критерии текучести также широко используются.
Три критерия
[ редактировать ]Критерий Треска основан на представлении о том, что разрушение материала происходит при сдвиге, что является относительно хорошим предположением при рассмотрении металлов. Учитывая основное напряженное состояние, мы можем использовать круг Мора, чтобы определить максимальные напряжения сдвига, которые испытает наш материал, и сделать вывод, что материал выйдет из строя, если
где σ1 σ3 — максимальное нормальное напряжение, — . минимальное нормальное напряжение, а σ0 — напряжение, при котором материал разрушается при одноосной нагрузке Может быть построена поверхность текучести , которая обеспечивает визуальное представление этой концепции. Внутри поверхности текучести деформация упругая. На поверхности деформация пластическая. Материал не может иметь напряженные состояния за пределами своей поверхности текучести.
Критерий Хубера – фон Мизеса
[ редактировать ]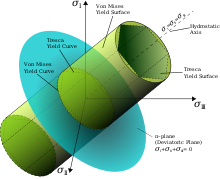
Критерий Хубера–фон Мизеса [ 13 ] основан на критерии Треска, но учитывает предположение о том, что гидростатические напряжения не способствуют разрушению материала. М.Т. Хубер был первым, кто предложил критерий сдвиговой энергии. [ 14 ] [ 15 ] Фон Мизес находит эффективное напряжение при одноосной нагрузке, вычитая гидростатические напряжения, и утверждает, что все эффективные напряжения, превышающие то, которое вызывает разрушение материала при одноосной нагрузке, приведут к пластической деформации.
Опять же, визуальное представление поверхности текучести может быть построено с использованием приведенного выше уравнения, которое принимает форму эллипса. Внутри поверхности материалы подвергаются упругой деформации. Достигнув поверхности, материал подвергается пластическим деформациям.
См. также
[ редактировать ]- Выход (инжиниринг)
- Пределы Аттерберга
- Деформация (механика)
- Деформация (инженерия)
- пластометр
- коэффициент Пуассона
Ссылки
[ редактировать ]- ^ Люблинер, Джейкоб (2008). Теория пластичности . Дувр. ISBN 978-0-486-46290-5 .
- ^ Бигони, Давиде (2012). Нелинейная механика твердого тела: теория бифуркаций и нестабильность материалов . Издательство Кембриджского университета. ISBN 978-1-107-02541-7 .
- ^ Йирасек, Милан; Бажант, Зденек П. (2002). Неупругий анализ конструкций . Джон Уайли и сыновья. ISBN 0-471-98716-6 .
- ^ Чен, Вай-Фа (2008). Предельный анализ и пластичность грунтов . Издательство Дж. Росс. ISBN 978-1-932159-73-8 .
- ^ Ю, Мао-Хун Хун-Фу, Юн-Цян (2006). Ма, Го - Вэй ; ; 3-540-25127-8 .
- ^ Чен, Вай-Фа (2007). Пластичность железобетона . Издательство Дж. Росс. ISBN 978-1-932159-74-5 .
- ^ Цигенхайн, Герольф; и Урбассек, Герберт М.; «Обратимая пластичность в ГЦК-металлах» в журнале Philosophical Magazine Letters , 89(11):717-723, 2009 г. , DOI 10.1080/09500830903272900.
- ^ Маас, Роберт; Дерлет, Питер М. (январь 2018 г.). «Микропластичность и последние открытия в области прерывистой и мелкомасштабной пластичности». Акта Материалия . 143 : 338–363. arXiv : 1704.07297 . Бибкод : 2018AcMat.143..338M . дои : 10.1016/j.actamat.2017.06.023 . S2CID 119387816 .
- ^ Кортни, Томас (2005). Механическое поведение материалов (второе изд.). Лонг-Гроув, Иллинойс: Waveland Press, Inc. ISBN 978-1-57766-425-3 .
- ^ Партридж, Питер (1969). Деформация и усталость гексагональных плотноупакованных металлов . Университет Суррея.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Гроувс, Джеффри В.; Келли, Энтони (1963). «Независимые системы скольжения в кристаллах». Философский журнал . 8 (89): 877–887. Бибкод : 1963PMag....8..877G . дои : 10.1080/14786436308213843 .
- ^ Хилл, Родни (1998). Математическая теория пластичности . Издательство Оксфордского университета. ISBN 0-19-850367-9 .
- ^ фон Мизес, Рихард (1913). «Механика твердых тел в пластически-деформируемом состоянии» . Новости Общества наук в Геттингене . Математико-физический класс. 1913 (1): 582–592.
- ^ Хубер, Максимилиан Титус (1904). «Удельная работа деформации как мера прочности материала». Технический журнал . 22 . Львов. Переведено как «Удельная работа напряжения как мера материального усилия» . Архив механики . 56 : 173–190. 2004.
- ^ См. Тимошенко, Стивен П. (1953). История сопротивления материалов . Нью-Йорк: МакГроу-Хилл. п. 369. ИСБН 9780486611877 .
Дальнейшее чтение
[ редактировать ]- Эшби, Майкл Ф. (2001). «Пластическая деформация ячеистых материалов». Энциклопедия материалов: наука и технологии . Том. 7. Оксфорд: Эльзевир. стр. 7068–7071. ISBN 0-08-043152-6 .
- Хан, Вэйминь; Редди, Б. Дайя (2013). Пластичность: математическая теория и численный анализ (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-1-4614-5939-2 .
- Качанов, Лазарь Маркович (2004). Основы теории пластичности . Дуврские книги. ISBN 0-486-43583-0 .
- Хан, Ахтар С.; Хуан, Суцзянь (1995). Континуальная теория пластичности . Уайли. ISBN 0-471-31043-3 .
- Симо, Хуан К.; Хьюз, Томас-младший (1998). Вычислительная неэластичность . Спрингер. ISBN 0-387-97520-9 .
- Ван Влит, Кристин Дж. (2006). «Механическое поведение материалов» . Курс MIT № 3.032 . Массачусетский технологический институт.




![{\displaystyle \sigma _{v}^{2}={\tfrac {1}{2}}[(\sigma _{11}-\sigma _{22})^{2}+(\sigma _{ 22}-\sigma _{33})^{2}+(\sigma _{11}-\sigma _{33})^{2}+6(\sigma _{23}^{2}+\sigma _{31}^{2}+\sigma _{12}^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/918b083c9c0c4f9cb190d778ecfdc3fd9eb6e4f9)