Редкая катастрофа

В экономике – редкая катастрофа это нечастый и крупный по масштабам коллапс , оказывающий негативное воздействие на экономику . Редкие катастрофы важны , поскольку они дают объяснение загадке премий по акциям , поведению процентных ставок и другим экономическим явлениям .

Параметрами редкой катастрофы являются существенное падение ВВП и снижение потребления как минимум на 10% . Примеры включают финансовые катастрофы : Великую депрессию и азиатский финансовый кризис 1997 года ; войны: Первая мировая война , Вторая мировая война и региональные конфликты; эпидемии : вспышки гриппа и азиатского гриппа; погодные явления; землетрясения ​ и цунами ; однако любое событие, оказывающее существенное влияние на ВВП и потребление, можно считать редкой катастрофой.

Идея была впервые предложена Ритцем в 1988 году. как способ объяснить загадку премии по акциям. С тех пор другие экономисты дополнили и подкрепили эту идею доказательствами, но многие экономисты по-прежнему скептически относятся к этой теории.

Модель

Модель, предложенная Барро, основана на модели Лукаса «фруктовое дерево» ценообразования активов с экзогенным стохастическим производством. Экономика закрыта, количество деревьев фиксировано, выпуск равен потреблению ( A _{t + 1} = C _t ), инвестиций и амортизации нет. As ( A _{t + 1} ) — это объем производства всех деревьев в экономике и ( ${P_{t}}$ ) — цена плодов периода (требование долевого участия). Уравнение ниже показывает валовую прибыль от фруктовых деревьев за один период.

$R={\frac {A_{t+1}}{P_{t1}}}$

Чтобы смоделировать редкие катастрофы, Барро вводит приведенное ниже уравнение, которое представляет собой стохастический процесс для совокупного роста производства. В модели выделяются три типа экономических шоков:

а.) Нормальные ид шоки
б.) Тип ( ${\tilde {w}}_{t+1}$) катастрофы, которые сопровождаются резким сокращением производства, но не дефолтом по долгам.
в.) Тип ( ${\tilde {v}}$) катастрофы, которые включают резкое сокращение производства и, по крайней мере, частичный дефолт по долгам.

$\log A_{t+1}=\log A_{t}+{\bar {g}}+{\tilde {u}}_{t+1}+{\tilde {v}}_{t+1}$

Тип ω ( ${\tilde {v}}_{t+1}$) моделирует бедствия малой вероятности и ( ${\tilde {u}}_{t+1}$) — случайная переменная iid. Предполагается, что они независимы, поэтому в уравнении они взаимозаменяемы. Тогда из приведенного выше уравнения величина сокращения от ( ${\tilde {v}}_{t+1}$) определяется следующим уравнением.

${\begin{cases}1&(e^{-p}){\mbox{ no disaster}}\\1-b&(1-e^{-p}){\mbox{ disaster}}\\\end{cases}}$

В этом уравнении p — вероятность возникновения катастрофы в единицу времени в каждый период. Если произойдет катастрофа, b будет фактором, на который сократится потребление. Модель требует маленького ap и такого большого ab для правильного моделирования редких катастроф. В анализе Барро d также используется для решения проблемы частичного дефолта по облигациям.

Приложения

Начиная с Ритца и Барро, концепция редких катастроф может быть использована для объяснения многих событий в финансах и экономике.

Премия за акции

Большая часть загадки премии по акциям может быть объяснена редкими сценариями катастроф, предложенными Барро и Ритцем. Основная причина заключается в том, что если люди осознают, что могут произойти редкие катастрофы (например, Великая депрессия или Первая и Вторая мировые войны), но катастрофы никогда не происходят в течение их жизни, тогда премия за акции будет казаться высокой.

Барро и последующие экономисты предоставили исторические доказательства в поддержку этого утверждения. Используя эти данные, Барро показывает, что редкие катастрофы происходят часто и в больших масштабах в экономиках по всему миру с периода с середины XIX века до наших дней.

Кроме того, данные показывают, что в долгосрочной перспективе премия за риск в большинстве стран составляет около 5,0%. Однако в определенные периоды времени эта премия может быть выше или ниже. Например, если рассматривать набор данных периода Великой депрессии, то премия за акции составит около 0,4%, поскольку Великая депрессия была редким бедствием.

Безрисковое поведение процентных ставок

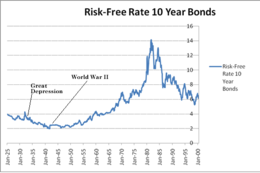
Безрисковая процентная ставка (проценты, полученные по фиксированному доходу, например, по облигациям, выпущенным чрезвычайно безопасными организациями, обычно правительствами) также может быть объяснена редкими катастрофами. Используя данные из США, модель редких бедствий показывает, что безрисковая ставка значительно падает (с 0,127 до 0,035), когда в набор данных вводится редкое бедствие с вероятностью 0,017.

Более того, Барро защищает критику поведения безрисковой ставки, высказанную Мехрой в отношении Великой депрессии и таких событий, как сброс атомной бомбы во время Второй мировой войны. Он считает, что ожидания людей относительно редких катастроф связаны с двумя эффектами: вероятностью редкой катастрофы и вероятностью дефолта . В случае возникновения вероятности ядерной войны (например, Карибского кризиса или Второй мировой войны) вероятность катастрофы возрастет и, следовательно, снизит процентные ставки. Однако вероятность государственного дефолта по облигациям также возрастает из-за возможного разрушения стран, что повышает ставку по облигациям. Эти две силы противодействуют, что приводит к двусмысленности. Как показано слева, безрисковая ставка росла до и падала после Великой депрессии, затем сначала упала во время Второй мировой войны, а затем выросла после нее.

История

Эдвард Прескотт и Раджниш Мехра впервые предложили загадку премии по акциям в 1985 году. предположил, что крупные и нечастые экономические потрясения могут объяснить премию за акции (премию долевых ценных бумаг над активами с фиксированным доходом). Однако в то время это считалось неосуществимым, поскольку казалось, что такие события слишком редки и не могут произойти в реальности. Теория была забыта до 2005 года, когда Роберт Барро представил свидетельства народов всего мира XIX и XX веков, доказав, что эти события были возможны и произошли. После его статей другие высказали разные идеи относительно влияния редких бедствий на другие экономические явления. Однако многие экономисты по-прежнему скептически относятся к тому, насколько редкие катастрофы действительно объясняют премию по акциям, а Мехра по-прежнему выражает сомнение в обоснованности теории.

Споры

Раджниш Мехра скептически отнесся к утверждению Рейца о том, что редкие катастрофы объясняют премию по акциям и поведение реальных процентных ставок, потому что редкая катастрофа, о которой говорил Ритц, никогда не происходила в США. Ритц предполагал падение от 25 до 97%, но этого никогда не происходило в Соединенных Штатах. Штаты. Даже если бы это было правдой, в его модели, параметрах и подтверждающих доказательствах есть еще несколько недостатков. Модель, представленная Ритцем, не компенсировала частичный дефолт держателей облигаций из-за быстрой инфляции. Кроме того, в его анализе непоследовательно использовался параметр неприятия риска. Например, значение 10 использовалось, чтобы показать падение потребления на 25%, а значение 1 используется для объяснения доходности акций и потребления. Наконец, было сказано, что необходимы дополнительные исторические свидетельства, чтобы дать теории должное подтверждение. Например, предполагаемая вероятность редкой катастрофы должна была быть низкой до того, как была сброшена атомная бомба, и должна была быть выше до кубинского ракетного кризиса, чем после. Следовательно, реальные процентные ставки должны были коррелировать с этими событиями, но этого не произошло. Мехра пришел к выводу, что сценарий Ритца был слишком радикальным, чтобы решить загадку.

См. также

• Редкие события

Ссылки

Библиография

• Раджниш Мехра (февраль 2003 г.). «Премиум акций: почему это загадка?» (PDF) . Проверено 9 марта 2009 г.
• Новый экономист (30 сентября 2005 г.). «Новый экономист по Барро и загадке премий на акции» . Мехра . Проверено 9 марта 2009 г.